스레드 이진 트리
Threaded binary tree| 그래프 및 트리 검색 알고리즘 |
|---|
| 최단 경로 |
| 목록 |
| 관련 항목 |
컴퓨팅에서 스레드 이진 트리는 특정한 순서(흔히 트리에 대해 이미 정의된 순서와 동일한 순서)로 횡단을 용이하게 하는 이진 트리 변종이다.
전체 바이너리 검색 트리는 주 키 순서로 쉽게 통과할 수 있지만 노드에 대한 포인터만 주어지면 다음에 오는 노드를 찾는 것이 느리거나 불가능할 수 있다.예를 들어 정의에 의한 리프 노드는 하위 노드가 없으므로 리프 노드에 대한 포인터만 주어지면 다른 노드에 도달할 수 없다.나사산 트리는 일부 노드 또는 모든 노드에 추가 정보를 추가하여 주어진 단일 노드에 대해 "다음" 노드를 신속하게 찾을 수 있으므로, 재귀 없이 트리 통과와 재귀에 필요한 추가 스토리지(트리 깊이에 비례함)가 가능하다.
스레딩
"이진 트리는 일반적으로 노드의 주문형 후속(존재하는 경우)에 null 포인터가 되는 모든 오른쪽 하위 포인터와 일반적으로 노드의 주문형 이전 버전에는 null 포인터가 되는 모든 왼쪽 하위 포인터를 만들어 스레드를 만든다."[1]
이는 통과 순서가 트리의 순서 내 통과와 동일하다고 가정한다.그러나 포인터는 대체하는 대신 트리 노드에 추가할 수 있다(또는 추가).이렇게 정의된 링크된 목록을 일반적으로 "스레드"라고도 하며 원하는 순서에 따라 통과를 활성화하는 데 사용할 수 있다.예를 들어, 노드가 사람에 대한 정보를 나타내는 트리는 이름별로 정렬될 수 있지만, 생년월일, 체중 또는 기타 알려진 특성의 순서로 빠르게 통과할 수 있는 여분의 스레드가 있다.
동기
바이너리 검색 트리를 포함한(그러나 이에 국한되지는 않음) 트리는 종종 키라고 불리는 각 노드에 저장된 일부 속성의 값과 같은 특정 순서로 항목을 저장하는 데 사용될 수 있다.그러한 트리에서 유용한 작업 중 하나는 통과다. 즉, 키 순서대로 모든 항목을 방문하는 것이다.
이진 검색 트리의 각 노드를 방문하는 간단한 재귀적 통과 알고리즘은 다음과 같다.t가 노드 또는 nil에 대한 포인터라고 가정하십시오."방문" t는 노드 t 또는 해당 컨텐츠에 대한 모든 작업을 수행하는 것을 의미할 수 있다.
알고리즘 다각측량(t):
- 입력: 노드(또는 nil)에 대한 포인터 t
- t = 0이면 반환한다.
- 기타:
- 다각측량(왼쪽-차일드(t))
- 방문 t
- 트래버스(우측-차일드(t))
이 알고리즘의 한 가지 문제는 재귀 때문에 나무의 높이에 비례하는 스택 공간을 사용한다는 것이다.트리가 상당히 균형 잡힌 경우, 이것은 n개의 원소를 포함하는 트리의 O(log n) 공간에 해당한다.최악의 경우 나무가 체인의 형태를 띠면 나무의 높이가 n이기 때문에 알고리즘은 O(n) 공간을 차지한다.두 번째 문제는 노드에 자식 전용 포인터가 있을 때 모든 트래버설이 기본적으로 시작되어야 한다는 것이다.특정 노드에 포인터를 두는 것이 일반적이지만, 스레드 포인터와 같은 추가 정보가 추가되지 않는 한 나무의 나머지 부분으로 돌아가기에는 충분하지 않다.
이 접근방식에서 주어진 노드의 왼쪽 및/또는 오른쪽 포인터가 실제로 어린이를 가리키는지 또는 나사산의 결과인지 구별할 수 없을 수 있다.구분이 필요한 경우 각 노드에 하나의 비트를 추가하면 충분히 녹화할 수 있다.
도널드 크누스는 1968년 교과서에서 스택을 사용하지 않고 트리를 수정하지 않은 채 방치하는 주문형 횡단을 위한 비재발 알고리즘이 존재하는지 물었다.[2]이 문제에 대한 해결책 중 하나는 1979년 조셉 M. 모리스에 의해 제시된 나무 나사산이다.[3][4]크누스는 1969년 후속 판에서 실타래 나무의 대표성을 펄리스와 쏜튼(1960년) 탓으로 돌렸다.[5][6]
상위 포인터와의 관계
유사한 목표를 달성하기 위한 또 다른 방법은 모든 노드의 상위 노드에 포인터를 포함하는 것이다.그 점을 감안하면, "다음" 노드에 항상 도달할 수 있다."오른쪽" 포인터는 올바른 아이들이 없을 때마다 여전히 무효다.오른쪽 포인터가 null인 노드에서 "다음" 노드를 찾으려면 오른쪽 포인터가 null이 아닌 노드에 도달할 때까지 "상위" 포인터를 따라 올라가십시오.그 노드는 "다음" 노드로, 그 노드가 오른편에 그 후손들이 온다.
또한 느리지만 부모 포인터나 스택을 명시적으로 사용하지 않고 스레드된 이진 트리에서 노드의 부모를 발견할 수도 있다.이를 확인하려면 오른쪽 자식 r이 있는 노드 k를 고려하십시오.그런 다음 r의 왼쪽 포인터는 k로 되돌아가는 어린이나 실 중 하나여야 한다.r이 왼쪽 아이를 갖는 경우, 그 왼쪽 아이는 차례로 자신의 왼쪽 아이를 가지거나 k로 돌아가는 실을 가져야 한다.그래서 r의 좌뇌 사슬을 따라가다 보면 결국 k를 가리키는 실이 발견될 것이다.q가 p의 왼쪽 아이일 때 상황은 대칭적으로 유사하다. q의 오른쪽 아이들을 p를 가리키는 실까지 따라갈 수 있다.
종류들
- 단일 스레드: 각 노드는 주문 중인 이전 노드 또는 후속 노드(왼쪽 또는 오른쪽)를 향해 스레드된다.
- 이중 스레드: 각 노드는 주문 중인 이전 노드와 후속 노드(왼쪽 및 오른쪽)를 모두 향해 스레드된다.
Python의 경우:
반항하다 부모(마디를 짓다): 만일 마디를 짓다 이다 마디를 짓다.나무.뿌리를 내리다: 돌아오다 없음 x = 마디를 짓다 y = 마디를 짓다 하는 동안에 진실의: 만일 is_message(y): p = y.맞다 만일 p 이다 없음 또는 p.남겨진 이다 아닌 마디를 짓다: p = x 하는 동안에 아닌 is_message(p.남겨진): p = p.남겨진 p = p.남겨진 돌아오다 p 엘리프 is_message(x): p = x.남겨진 만일 p 이다 없음 또는 p.맞다 이다 아닌 마디를 짓다: p = y 하는 동안에 아닌 is_message(p.맞다): p = p.맞다 p = p.맞다 돌아오다 p x = x.남겨진 y = y.맞다 순서 내 통과 배열
스레드는 inorder traversal에 따라 노드의 이전자와 후속자를 가리킨다.
스레드 트리의 순서 내 통과는A,B,C,D,E,F,G,H,I, 의 전신E이다D, 의 후계자E이다F.
예
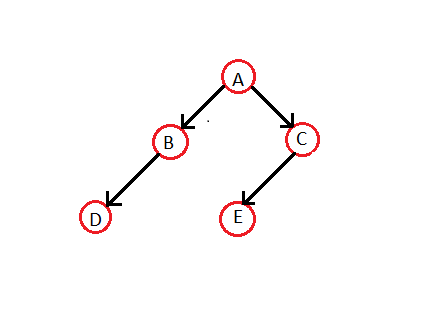
일반 이진 트리에서 스레드 이진 트리를 만들자:
위의 트리에 대한 순서 내 통과는 — D B A E C. 따라서 각 스레드 이진 트리는 --
Null 링크
n개의 노드가 있는 m-way 스레드 이진 트리에는 n*m - (n-1) 보이드 링크가 있다.
참조
- ^ Van Wyk, Christopher J. Data Structures and C Programs, Addison-Wesley, 1988, 페이지 175. ISBN978-0-201-16116-8.
- ^ Knuth, D.E. (1968). Fundamental Algorithms. The Art of Computer Programming. Vol. 1 (1st ed.). Reading/MA: Addison Wesley.
- ^ Morris, Joseph H. (1979). "Traversing binary trees simply and cheaply". Information Processing Letters. 9 (5). doi:10.1016/0020-0190(79)90068-1.
- ^ Mateti, Prabhaker; Manghirmalani, Ravi (1988). "Morris' tree traversal algorithm reconsidered". Science of Computer Programming. 11: 29–43. doi:10.1016/0167-6423(88)90063-9.
- ^ Knuth, D.E. (1969). Fundamental Algorithms. The Art of Computer Programming. Vol. 1 (2 ed.). Addison Wesley. Hre: 제2.3.1장 "트래버싱 이진수"
- ^ Perlis, Alan Jay; Thornton, C. (Apr 1960). "Symbol manipulation by threaded lists". Communications of the ACM. 3 (4): 195–204. doi:10.1145/367177.367202.