토폴리 게이트

Toffoli gate
Topfoli 게이트의 회로 표현

논리회로에서 토마소 토폴리에 의해 발명된 토폴리 게이트(또한 CCNOT 게이트)는 범용 가역 논리 게이트로, 모든 고전 가역 회로가 토폴리 게이트에서 구성될 수 있음을 의미합니다.그것은 또한 그것의 작용을 설명하는 "제어된-제어되지 않은" 게이트로 알려져 있다.3비트 입력 및 출력이 있습니다. 처음 두 비트가 모두 1로 설정되어 있으면 세 번째 비트를 반전시키고, 그렇지 않으면 모든 비트가 동일하게 유지됩니다.

배경

입력 소비형 논리 게이트 L은 다음 조건을 만족하는 경우 가역적입니다. L(x) = y는 출력 y에 대해 고유한 입력 x가 존재하는 게이트입니다.게이트 L은 y와 x를 매핑하는 게이트 Lδ(y) = x가 있으면 가역적입니다. 공통 논리 게이트에서 NOT는 아래의 진실 표에서 볼 수 있듯이 가역입니다.

입력 산출량
0 1
1 0

입력 00, 01, 10은 모두 출력 0에 매핑되므로 공통 AND 게이트는 되돌릴 수 없습니다.

가역문은 1960년대부터 연구되어 왔다.원래 동기는 가역 게이트가 열을 덜 발산하는 것(또는 원칙적으로 [1]열이 없는 것)이었다.

최근의 동기는 양자 컴퓨팅에서 비롯됩니다.양자역학에서 양자상태는 슈뢰딩거 방정식(유니터리 변환)에 의해 또는 붕괴에 의해 두 가지 방법으로 진화할 수 있다.양자컴퓨터의 논리연산은 Topfoli 게이트를 예로 들며 단일 변환이므로 [2]가역적으로 진화한다.

유니버설리티와 토폴리 게이트

입력을 소비하고 모든 입력 계산을 허용하는 모든 리버서블 게이트는 피죤홀 원리에 따라 출력 비트보다 더 많은 입력 비트를 가질 수 없습니다.1개의 입력 비트에 대해 2개의 가능한 가역 게이트가 있습니다.그들 중 하나는 아니다.다른 하나는 ID 게이트입니다.ID 게이트는 입력을 변경하지 않고 출력에 매핑합니다.2개의 입력 비트의 경우 단순한 게이트가 아닌 유일한 게이트는 제어된 NOT 게이트입니다.이 게이트는 첫 번째 비트를 두 번째 비트로 XOR하고 첫 번째 비트를 변경하지 않습니다.

진실표 치환 행렬 형식
입력 산출량
0 0 0 0
0 1 0 1
1 0 1 1
1 1 1 0

안타깝게도 이러한 게이트만 사용하여 계산할 수 없는 가역 함수가 있습니다.즉, NOT 게이트와 XOR 게이트로 구성된 세트는 유니버설하지 않습니다.가역 게이트를 사용하여 임의 함수를 계산하려면 다른 게이트가 필요합니다.한 가지 가능성은 1980년 토폴리에 [3]의해 제안된 토폴리 게이트이다.

이 게이트에는 3비트 입력 및 출력이 있습니다.첫 번째 2비트가 설정되어 있는 경우 세 번째 비트가 플립됩니다.다음은 입력 및 출력 비트의 표입니다.

진실표 치환 행렬 형식
입력 산출량
0 0 0 0 0 0
0 0 1 0 0 1
0 1 0 0 1 0
0 1 1 0 1 1
1 0 0 1 0 0
1 0 1 1 0 1
1 1 0 1 1 1
1 1 1 1 1 0

비트 {a, b, c}를 {a, b, c XOR(a AND b)}에 매핑하는 것으로도 설명할 수 있습니다.

Topfoli 게이트는 범용입니다. 즉, 부울 함수 f(x1, x2, ..., xm)에 대해 x, x2, ..., xm 및 x, f2(x1, x2, ..., xm) 및m 일부 추가 비트(가비지)를1 출력하기 위해1 0 또는 1로 설정된 Topfoli 게이트로 구성된 회로가 있음을 의미합니다.예를 들어, 3개의 입력 비트를 {a, 1, 1}(으)로 설정하여 NOT 게이트를 구성할 수 있으며, 세 번째 출력 비트(1 XOR (a AND 1) = NOT a; (a AND b)는 {a, b, 0}의 세 번째 출력 비트입니다.기본적으로 이는 Topfoli 게이트를 사용하여 원하는 부울 함수 계산을 역방향으로 수행하는 시스템을 구축할 수 있음을 의미합니다.

관련 로직 게이트

Topfoli 게이트는 단일 큐비트게이트와 최소 6개의 CNOT로 구성할 수 있습니다.
  • Fredkin 게이트는 첫 번째 비트가 1일 경우 마지막 2비트를 스왑하는 범용 리버서블 3비트 게이트입니다.즉, 제어된 스왑 동작입니다.
  • n비트 Topfoli 게이트는 Topfoli 게이트의 일반화입니다.입력1 및 출력에는 n비트 x2, xn, ..., x가 필요합니다.첫 번째 n-1 출력 비트는 x1, ..., x입니다n−1. 마지막 출력 비트는 (x1 AND ...)입니다.AND xn−1) XOR xn.
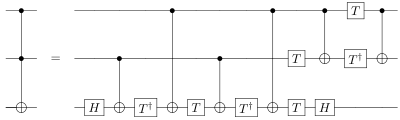
  • 토폴리 게이트는 5개의 2비트 양자 [4]게이트로 실현될 수 있지만 [5]5개 미만으로 실현될 수 없다는 것을 보여줄 수 있다.
  • 관련된 양자 게이트인 Deutsch 게이트는 중성 [6]원자를 가진 5개의 광학 펄스에 의해 실현될 수 있습니다.독일 게이트는 양자 컴퓨팅의 범용 [7]게이트입니다.

양자 컴퓨팅과의 관계

양자 컴퓨터에서는 모든 가역 게이트를 구현할 수 있으므로 토폴리 게이트는 양자 연산자이기도 합니다.그러나 토폴리 게이트는 양자 컴퓨터가 모든 가능한 고전적 계산을 구현할 수 있다는 것을 의미하지만 범용 양자 계산에 사용할 수 없습니다.토폴리 게이트는 양자 계산을 위해 보편화되기 위해 일부 본질적으로 양자 게이트와 함께 구현되어야 한다.사실, 중요하지 않은 양자 상태를 만들 수 있는 실제 계수를 가진 모든 단일 큐비트 게이트로 [8]충분합니다.양자역학에 기초한 토폴리 게이트는 2009년 1월 오스트리아 [9]인스브루크 대학에서 성공적으로 실현되었다.회선 모델을 사용한n 큐비트 Topfoli의 실장에는 2n의 [10]CNOT 게이트가 필요하지만 가장 잘 알려진 상한은 6n-12의 CNOT [11]게이트입니다.포획된 이온 퀀텀 컴퓨터는 n-qubit Toffoli 게이트를 [12]직접 구현할 수 있을 것으로 제안되었습니다.다체 상호작용의 적용은 포획 이온, Rydberg 원자 및 초전도 회로 [13][14][15][16]구현에서 게이트의 직접 작동에 사용될 수 있다.다크 스테이트 매니폴드에 이어 Khazali-Mölmer C-NOTn[14] 게이트는 회로 모델 패러다임에서 벗어나 3개의 펄스만으로 작동합니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ Landauer, R. (July 1961). "Irreversibility and Heat Generation in the Computing Process". IBM Journal of Research and Development. 5 (3): 183–191. doi:10.1147/rd.53.0183. ISSN 0018-8646.
  2. ^ Colin P. Williams (2011). Explorations in Quantum Computing. Springer. pp. 25–29, 61. ISBN 978-1-84628-887-6.
  3. ^ 기술 보고서 MIT/LCS/TM-151(1980년)과고 요약한 편곡:.Toffoli, 토마소(1980년).J.W. 드 바커와 제이 밴 레이우엔(교육.).가역적 컴퓨팅(PDF).자동자, 언어와 프로그래밍, 7콜로퀴움.Noordwijkerhout, 네덜란드:스프링거 출판사..를 대신하여 서명함. 632–644. doi:10.1007/3-540-10003-2_104.아이 에스비엔 3-540-10003-2.2010-04-15에 있는 원본(PDF)에서 Archived.
  4. ^ Barenco, Adriano; Bennett, Charles H.; Cleve, Richard; DiVincenzo, David P.; Margolus, Norman; Shor, Peter; Sleator, Tycho; Smolin, John A.; Weinfurter, Harald (Nov 1995). "Elementary gates for quantum computation". Physical Review A. 52 (5): 3457–3467. arXiv:quant-ph/9503016. Bibcode:1995PhRvA..52.3457B. doi:10.1103/PhysRevA.52.3457. PMID 9912645. S2CID 8764584.
  5. ^ Yu, Nengkun; Duan, Runyao; Ying, Mingsheng (2013-07-30). "Five two-qubit gates are necessary for implementing the Toffoli gate". Physical Review A. 88 (1): 010304. arXiv:1301.3372. Bibcode:2013PhRvA..88a0304Y. doi:10.1103/physreva.88.010304. ISSN 1050-2947. S2CID 55486826.
  6. ^ Shi, Xiao-Feng (May 2018). "Deutsch, Toffoli, and CNOT Gates via Rydberg Blockade of Neutral Atoms". Physical Review Applied. 9 (5): 051001. arXiv:1710.01859. Bibcode:2018PhRvP...9e1001S. doi:10.1103/PhysRevApplied.9.051001. S2CID 118909059.
  7. ^ Deutsch, D. (1989). "Quantum Computational Networks". Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 425 (1868): 73–90. Bibcode:1989RSPSA.425...73D. doi:10.1098/rspa.1989.0099. ISSN 0080-4630. JSTOR 2398494. S2CID 123073680.
  8. ^ Shi, Yaoyun (Jan 2003). "Both Toffoli and Controlled-NOT need little help to do universal quantum computation". Quantum Information & Computation. 3 (1): 84–92. arXiv:quant-ph/0205115. Bibcode:2002quant.ph..5115S. doi:10.26421/QIC3.1-7.
  9. ^ Monz, T.; Kim, K.; Hänsel, W.; Riebe, M.; Villar, A. S.; Schindler, P.; Chwalla, M.; Hennrich, M.; Blatt, R. (Jan 2009). "Realization of the Quantum Toffoli Gate with Trapped Ions". Physical Review Letters. 102 (4): 040501. arXiv:0804.0082. Bibcode:2009PhRvL.102d0501M. doi:10.1103/PhysRevLett.102.040501. PMID 19257408. S2CID 2051775.
  10. ^ Shende, Vivek V.; Markov, Igor L. (2008-03-15). "On the CNOT-cost of TOFFOLI gates". arXiv:0803.2316 [quant-ph].
  11. ^ Maslov, Dmitri (2016). "Advantages of using relative-phase Toffoli gates with an application to multiple control Toffoli optimization". Physical Review A. 93 (2): 022311. arXiv:1508.03273. Bibcode:2016PhRvA..93b2311M. doi:10.1103/PhysRevA.93.022311. S2CID 5226873.
  12. ^ Katz, Or; Cetina, Marko; Monroe, Christopher (2022-02-08). "N-body interactions between trapped ion qubits via spin-dependent squeezing". arXiv:2202.04230 [quant-ph].
  13. ^ Arias Espinoza, Juan Diego; Groenland, Koen; Mazzanti, Matteo; Schoutens, Kareljan; Gerritsma, Rene (2021-05-28). "High-fidelity method for a single-step N-bit Toffoli gate in trapped ions". Physical Review A. 103 (5): 052437. arXiv:2010.08490. Bibcode:2021PhRvA.103e2437E. doi:10.1103/PhysRevA.103.052437. S2CID 223953418.
  14. ^ a b Khazali, Mohammadsadegh; Mølmer, Klaus (2020-06-11). "Fast Multiqubit Gates by Adiabatic Evolution in Interacting Excited-State Manifolds of Rydberg Atoms and Superconducting Circuits". Physical Review X. 10 (2): 021054. Bibcode:2020PhRvX..10b1054K. doi:10.1103/PhysRevX.10.021054. ISSN 2160-3308.
  15. ^ Isenhower, L.; Saffman, M.; Mølmer, K. (2011-09-04). "Multibit CkNOT quantum gates via Rydberg blockade". Quantum Information Processing. 10 (6): 755. arXiv:1104.3916. doi:10.1007/s11128-011-0292-4. ISSN 1573-1332. S2CID 28732092.
  16. ^ Rasmussen, S. E.; Groenland, K.; Gerritsma, R.; Schoutens, K.; Zinner, N. T. (2020-02-07). "Single-step implementation of high-fidelity n -bit Toffoli gates". Physical Review A. 101 (2): 022308. arXiv:1910.07548. Bibcode:2020PhRvA.101b2308R. doi:10.1103/physreva.101.022308. ISSN 2469-9926. S2CID 204744044.

외부 링크