활공 반사
Glide reflection이 기사는 대부분의 독자들이 이해하기에는 너무 전문적일 수 있다.내용을 도쉽게 할 수 있도록 개선 . (2016년 12월 (이 삭제 방법 및) |
2차원 기하학에서 활공 반사(또는 변환)는 한 선 위의 반사로 구성된 대칭 연산이며, 그 선을 따라 한 번의 연산으로 결합됩니다.반사와 변환 사이의 중간 단계는 시작 구성과 다르게 보일 수 있으므로 일반적으로 활공 대칭을 가진 물체는 반사만으로 대칭이 되지 않습니다.군 이론에서, 활공면은 유클리드 평면의 반대 등각계의 한 종류로 분류된다.
단일 활공기를 프리즈군 p11g으로 한다.활공반사는 회전이 변환이 되는 제한적인 회전반사로 볼 수 있다.또한 S로2∞ 쇤플라이 표기법, [,,+2+]로 콕서터 표기법, orbifold 표기법도 θ×로 지정할 수 있다.
묘사
한 선에서의 반사와 수직 방향에서의 변환의 조합은 평행한 선에서의 반사입니다.그러나 그렇게 활공 반사를 줄일 수는 없다.따라서 모든 번역과 결합된 반사의 효과는 활공 반사이며, 특별한 경우에는 반사일 뿐이다.이것들은 2D의 두 종류의 간접등각선입니다.
예를 들어, x축의 반사로 이루어진 등각도와 그에 평행한 한 단위의 변환이 있다.좌표에서, 그것은
이 등각은 x축을 그 자체에 매핑합니다.x축에 평행한 다른 선은 x축에 반영되므로 이 평행선 시스템은 변하지 않습니다.
활공 반사만으로 생성된 등각군은 무한 순환군이다.[1]
두 개의 동일한 활공 반사를 결합하면 활공 반사의 두 배인 변환 벡터와 순수 변환이 이루어지기 때문에 활공 반사의 짝수 세기가 변환 그룹을 형성합니다.
활공반사대칭의 경우 물체의 대칭군은 활공반사를 포함하고 이에 의해 생성되는 군이다.그것이 전부라면, 이 타입은 frize group p11g 입니다.
이 대칭 그룹의 패턴 예:
Frieze군 nr. 6(활공반사, 번역 및 회전)은 활공반사와 반사선상의 한 점에 대한 회전에 의해 생성된다.Z와2 C의 반직접적과 동형이다.
이 대칭 그룹의 패턴 예:
일상생활에서 활공 반사의 전형적인 예는 해변을 걷는 사람이 모래에 남긴 발자국일 것이다.
어떤 활공반사대칭을 포함하는 대칭군에 대하여 활공반사의 변환벡터는 변환군 요소의 절반이다.활공반사의 번역벡터 자체가 번역군의 요소라면 대응하는 활공반사대칭은 반사대칭과 번역대칭의 조합으로 감소한다.
같은 변환의 평행선 2개에 대한 활공반사대칭은 이들 선에 수직인 방향으로도 대칭이 존재하며, 그 변환거리는 활공반사선 사이의 거리의 2배임을 의미한다.이는 벽지 그룹 pg에 해당하며, 추가적인 대칭을 통해 pmg, pgg 및 p4g에서도 발생합니다.
같은 방향으로도 실제 반사선이 있는 경우 활공 반사선 사이에 균등하게 배치됩니다.실제 반사선과 평행한 활공 반사선은 이미 이러한 상황을 암시합니다.이것은 벽지 그룹 cm에 대응합니다.변환 대칭은 실제 반사선의 한 지점에서 다음 두 지점까지의 대각선 변환 벡터에 의해 주어지며, 실제 반사선을 대각선 중 하나로 하는 마름모꼴을 지지한다.대칭이 추가되면 cmm, p3m1, p31m, p4m 및 p6m에서도 발생합니다.
3D에서는 활공 반사를 활공 평면이라고 합니다.평면에 평행한 변환과 결합된 평면의 반사입니다.
벽지 그룹
유클리드 평면 3에서는 17개의 벽지 그룹이 활공 반사 발생기를 필요로 한다.p2gg는 직교 활공 반사와 2배 회전한다.cm에는 평행 거울과 활공, pg에는 평행 활공(활공 반사는 아래 점선으로 표시)이 있습니다.
| 결정학명 | pgg | cm | 페이지 |
|---|---|---|---|
| 콘웨이명 | 22× | *× | ×× |
| 도표 |  |  | 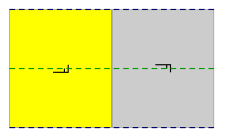 |
| 예 | 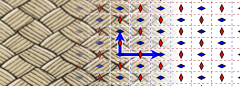 |  |  |
자연과 게임에 대한 활공 반사
글라이드 대칭은 에디아카라 생물군의 특정 화석, 마카에리아류,[2] 그리고 특정 고엽충류 사이에서 자연에서 관찰될 수 있다.그것은 또한 현존하는 많은 바다펜 [3]집단에서도 볼 수 있다.
Gun(셀룰러 오토마톤)을 제작할 때 Game of Life(Game of Life)에서는 활공 반사가 일반적입니다.
「 」를 참조해 주세요.
해당 3D 대칭 작업의 경우
레퍼런스
- ^ 를 클릭합니다Martin, George E. (1982). Transformation Geometry: An Introduction to Symmetry. Undergraduate Texts in Mathematics. Springer. p. 64. ISBN 9780387906362..
- ^ Waggoner, B. M. (1996). "Phylogenetic Hypotheses of the Relationships of Arthropods to Precambrian and Cambrian Problematic Fossil Taxa". Systematic Biology. 45 (2): 190–222. doi:10.2307/2413615. JSTOR 2413615.
- ^ Zubi, Teresa (2016-01-02). "Octocorals (Stoloniferans, soft corals, sea fans, gorgonians, sea pens) - Starfish Photos - Achtstrahlige Korallen (Röhrenkorallen, Weichkorallen, Hornkoralllen, Seefedern, Fächerkorallen)". starfish.ch. Retrieved 2016-09-08.




