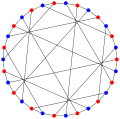
투테-콕시터 그래프
Tutte–Coxeter graph| 투테-콕시터 그래프 | |
|---|---|
 | |
| 이름을 따서 명명됨 | W. T. 투테 H. S. M. 콕시터 |
| 정점 | 30 |
| 가장자리 | 45 |
| 반지름 | 4 |
| 지름 | 4 |
| 둘레 | 8 |
| 자동형성 | 1440(Aut(S6)) |
| 색수 | 2 |
| 색도 지수 | 3 |
| 책두께 | 3 |
| 대기열 번호 | 2 |
| 특성. | 큐빅 케이지 무어 그래프 대칭 거리-정규어 거리-변환 양립자 |
| 그래프 및 모수 표 | |
그래프 이론의 수학 분야에서는 투트-콕시터 그래프나 투트 8-케이지 또는 크레모나-리치몬드 그래프는 정점 30개와 가장자리 45개를 가진 3-정규 그래프다.8번째 소녀 특유의 가장 작은 입방형 그래프로 케이지와 무어 그래프다.초당적이며 일반화된 쿼드랑글 W2(Cremona-Richmond 구성으로 알려져 있음)의 Levi 그래프로 구성할 수 있다.이 그래프는 윌리엄 토마스 투테와 H. S. M. 콕시터의 이름을 따서 명명되었다. 투테(1947년)에 의해 발견되었지만, 기하학적 구성과의 연관성은 공동 발표된 한 쌍의 논문에서 두 저자에 의해 조사되었다(Tutte 1958; Coxeter 1958a).
세제곱 거리-정규 그래프는 모두 알려져 있다.[1]Tutte-Coxeter는 13개의 그래프 중 하나이다.
13번 [2][3]교차점, 3번 책 두께, 2번 대기열이 있다.[4]
구성 및 자동화
특히 투테-콕시터 그래프의 조합 구성은 실베스터(1844년)의 작업에 기초한 콕시터(1958b) 때문이다.현대 용어로는 6개의 꼭지점 K에6 대한 완전한 그래프를 취한다.그것은 15개의 가장자리와 15개의 완벽한 짝을 가지고 있다.Tute-Coxeter 그래프의 각 꼭지점은 K의6 가장자리 또는 완벽한 일치에 해당하며, Tute-Coxeter 그래프의 각 가장자리는 K의6 완벽한 일치를 세 가지 구성요소 가장자리와 각각 연결한다.대칭에 의해 K의6 각 가장자리는 세 개의 완벽한 일치에 속한다.우연히, 정점을 가장자리-수직 및 일치-수직으로 분할하는 것은 Tute-Coxeter 그래프가 초당적이라는 것을 보여준다.
이 구성을 바탕으로 Coxeter는 Tutte-Coxeter 그래프가 대칭 그래프라는 것을 보여주었다; 1440 자동화 그룹을 가지고 있는데, 이는 6개 원소(Coxeter 1958b)에 대한 순열 그룹의 자동화와 동일할 수 있다.이 그룹의 내부 자동화는 K6 그래프의 6개 정점을 허용하는데 해당하며, 이러한 순열은 양면을 각각 세트로 고정시키면서 양분할의 양쪽에 정점을 허용함으로써 Tutte-Coxeter 그래프에 작용한다.또한 순열 그룹의 외부 자동화는 양분 중 한쪽을 다른 쪽과 교환한다.Coxeter가 보여주었듯이, Tutte-Coxeter 그래프에서 최대 5개의 가장자리의 어떤 경로는 그러한 자동화에 의해 다른 어떤 경로와 동등하다.
건물로서의 Tutte-Coxeter 그래프
이 그래프는 S 4( 2) 이 그룹과 대칭 그룹 사이에 예외적으로 이형성이 있다.좀 더 구체적으로 말하면 일반화된 사각형의 발병률 그래프다.
구체적으로 Tute-Coxeter 그래프는 F 2}}의 4차원 동시 벡터 V 에서 다음과 같이 정의할 수 있다.
- 정점은 0이 아닌 벡터 또는 등방성 2차원 서브스페이스,
- non W {\displaystyle 인 경우에만 0이 아닌 벡터 v와 등방성 2차원 아공간 사이에 에지가 있다
갤러리
참조
- ^ 브루워 A. E., 코헨 A. M., 노이마이어 A.거리-일반 그래프.뉴욕: 스프링거-베를라크, 1989.
- ^ Pegg, E. T.; Exoo, G. (2009). "Crossing Number Graphs". Mathematica Journal. 11 (2). doi:10.3888/tmj.11.2-2.
- ^ Exoo, G. "Rectilinear Drawings of Famous Graphs".
- ^ Wolz, Jessica; SAT를 이용한 엔지니어링 선형 레이아웃.2018년 튀빙겐 대학교 석사 논문
- Coxeter, H. S. M. (1958a). "The chords of the non-ruled quadric in PG(3,3)". Can. J. Math. 10: 484–488. doi:10.4153/CJM-1958-047-0.
- Coxeter, H. S. M. (1958b). "Twelve points in PG(5,3) with 95040 self-transformations". Proceedings of the Royal Society A. 247 (1250): 279–293. doi:10.1098/rspa.1958.0184. JSTOR 100667. S2CID 121676627.
- Sylvester, J. J. (1844). "Elementary researches in the analysis of combinatorial aggregation". Phil. Mag. Series 3. 24: 285–295. doi:10.1080/14786444408644856.
- Tutte, W. T. (1947). "A family of cubical graphs". Proc. Cambridge Philos. Soc. 43 (4): 459–474. doi:10.1017/S0305004100023720.
- Tutte, W. T. (1958). "The chords of the non-ruled quadric in PG(3,3)". Can. J. Math. 10: 481–483. doi:10.4153/CJM-1958-046-3.
외부 링크
- François Labelle. "3D Model of Tutte's 8-cage".
- Weisstein, Eric W. "Levi Graph". MathWorld.
- Exoo, G. "유명 그래프의 직선화 도면" [1]