레비 그래프
Levi graph| 레비 그래프 | |
|---|---|
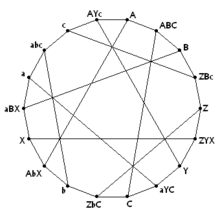 Pappus 그래프, 18개의 꼭지점이 Pappus 구성에서 형성되는 Levi 그래프.단일 문자로 표시된 정점은 구성의 점에 해당하며, 세 개의 문자로 표시된 정점은 세 점을 통과하는 선에 해당한다. | |
| 둘레 | ≥ 6 |
| 그래프 및 모수 표 | |
결합수학에서 Levi 그래프 또는 발생 그래프는 발생 구조와 연관된 초당적 그래프다.[1][2]입사 기하학 또는 투영 구성의 점 및 선 집합에서 우리는 점당 하나의 꼭지점, 선당 하나의 꼭지점, 점과 선 사이의 모든 입사점에 대한 가장자리를 가진 그래프를 형성한다.이 책들은 1942년에 이들에 대해 쓴 프리드리히 빌헬름 레비의 이름을 따서 지어졌다.[1][3]
점 및 선 시스템의 Levi 그래프는 보통 둘레가 6개 이상이다: 모든 4주기는 동일한 두 점을 통과하는 두 개의 선에 해당한다.반대로 둘레가 최소 6개인 초당적 그래프는 추상적 발생 구조의 Levi 그래프로 볼 수 있다.[1]구성의 Levi 그래프는 2각형이며, 최소 6개의 둘레가 있는 모든 2각형 그래프는 추상적 구성의 Levi 그래프로 볼 수 있다.[4]
Levi 그래프는 또한 유클리드 공간에서 점과 평면 사이의 발생과 같은 다른 유형의 발생 구조에 대해 정의될 수 있다.모든 Levi 그래프에는 등가 하이퍼그래프가 있으며, 그 반대의 경우도 있다.
예
히우드 그래프와 파노 평면
꼭지점 3은 원형 가장자리(3, 5, 6), 대각선 가장자리(3, 7, 4) 및 측면 가장자리(1, 3, 2, 3, 2)의 일부다.
꼭지점 3은 원형 가장자리(3, 5, 6), 대각선 가장자리(3, 7, 4) 및 측면 가장자리(1, 3, 2, 3, 2)의 일부다.
- 데스아게네스 그래프는 데스아게스 구성을 나타내는 레비 그래프로, 10점과 10선으로 구성되어 있다.각 선에는 3개의 점이 있고, 각 점을 통과하는 3개의 선이 있다.데스아게네스 그래프는 일반화된 피터슨 그래프 G(10,3) 또는 파라미터가 5,2인 초당파 크네세르 그래프로도 볼 수 있다.정점이 20개 있는 3정칙이다.
- 히우드 그래프는 파노 평면의 레비 그래프다.(3,6)-cage라고도 하며, 정점 14개로 3-정기다.
- 뫼비우스-칸토르 그래프는 뫼비우스-칸토르 구성의 레비 그래프로서, 유클리드 평면에서 직선으로는 실현할 수 없는 8점 8선의 시스템이다.정점이 16개 있는 3정기다.
- 파푸스 그래프(Pappus graph)는 파푸스 구성의 Levi 그래프로서, 9개의 점과 9개의 선으로 구성되어 있다.데스아게스 구성처럼 각 선에 3개의 점이 있고 각 점을 통과하는 3개의 선이 있다.정점이 18개 있는 3정칙이다.
- 회색 그래프는 R 에서 포인트의 3x 3 3 그리드와 이를 통해 27개의 직교선으로 실현될 수 있는 구성을 Levi 그래프로 나타낸 것이다.
- 투트 8-케이지(Tutte 8-cage)는 크레모나-리치몬드 구성을 나타내는 리바이스 그래프다.(3,8)-cage라고도 하며, 정점이 30개인 3-정기다.
- 4차원 하이퍼큐브 그래프 4 는 상호 입사 4면체의 점과 평면으로 형성된 뫼비우스 구성을 나타내는 Levi 그래프다.
- 112 정점에 있는 Ljubljana 그래프는 Ljubljana 구성의 Levi 그래프다.[5]
참조
- ^ a b c 특히 181쪽을 보라Grünbaum, Branko (2006), "Configurations of points and lines", The Coxeter Legacy, Providence, RI: American Mathematical Society, pp. 179–225, MR 2209028.
- ^ Polster, Burkard (1998), A Geometrical Picture Book, Universitext, New York: Springer-Verlag, p. 5, doi:10.1007/978-1-4419-8526-2, ISBN 0-387-98437-2, MR 1640615.
- ^ Levi, F. W. (1942), Finite Geometrical Systems, Calcutta: University of Calcutta, MR 0006834.
- ^ Gropp, Harald (2007), "VI.7 Configurations", in Colbourn, Charles J.; Dinitz, Jeffrey H. (eds.), Handbook of combinatorial designs, Discrete Mathematics and its Applications (Boca Raton) (Second ed.), Chapman & Hall/CRC, Boca Raton, Florida, pp. 353–355.
- ^ Conder, Marston; Malnič, Aleksander; Marušič, Dragan; Pisanski, Tomaž; Potočnik, Primož (2002), The Ljubljana Graph (PDF), IMFM Preprint 40-845, University of Ljubljana Department of Mathematics.




 상호 입사 4면체의 점과 평면으로 형성된
상호 입사 4면체의 점과 평면으로 형성된 
