가법합성
Additive synthesis가법 합성은 사인파를 [1][2]합산해 음색을 내는 음향 합성 기법이다.
악기의 음색은 푸리에 이론의 관점에서 복수의 고조파 또는 부조화파 부분 또는 음조로 구성된다고 생각할 수 있다.각 파셜은 ADSR 엔벨롭 또는 저주파 발진기의 변조로 인해 시간이 지남에 따라 팽창하고 감소하는 주파수와 진폭이 다른 사인파입니다.
가법 합성은 여러 사인파 발생기의 출력을 추가하여 가장 직접적으로 소리를 생성합니다.대체 구현에서는 미리 계산된 웨이브 테이블 또는 역고속 푸리에 변환을 사용할 수 있습니다.
설명.
일상생활에서 들리는 소리는 하나의 주파수로 특징지어지지 않는다.대신 각각 다른 진폭의 순수 사인 주파수의 합으로 구성됩니다.인간이 이 주파수를 동시에 들을 때, 우리는 소리를 인식할 수 있다.이는 "음악적이지 않은" 소리(예: 물이 튀는 소리, 나뭇잎이 바스락거리는 소리 등)와 "음악적인 소리"(예: 피아노 음표, 새소리 등) 모두에 해당된다.이 파라미터 세트(주파수, 상대진폭 및 시간에 따른 상대진폭 변화)는 소리의 음색으로 캡슐화됩니다.푸리에 분석은 전체 음성 신호에서 이러한 정확한 음색 매개 변수를 결정하는 데 사용되는 기술입니다. 반대로, 주파수 및 진폭의 결과 집합을 원래 음성 신호의 푸리에 시리즈라고 합니다.
음표의 경우 음색의 최저 주파수를 소리의 기본 주파수로 한다.단순화를 위해 음의 소리가 다른 많은 주파수로 구성되어 있음에도 불구하고, 우리는 종종 음이 그 기본 주파수(예: "중간 C는 261.6Hz")[3]로 재생된다고 말한다.나머지 주파수 세트를 [4]소리의 오버톤(또는 주파수가 기본 주파수의 정수 배수인 경우 고조파)이라고 합니다.즉, 음의 음높이는 기본 주파수만으로 결정되며, 음색은 소리의 음색을 정의합니다.중간 C를 연주하는 피아노의 음색은 같은 음을 연주하는 바이올린의 음색과 상당히 다를 것이다. 그것이 우리가 두 악기의 소리를 구별할 수 있게 해준다.심지어 같은 악기의 다른 버전들(예를 들어, 업라이트 피아노 대 그랜드 피아노) 사이에는 음색의 미묘한 차이가 있다.
가법 합성은 음색을 처음부터 구성하기 위해 소리의 특성을 이용하는 것을 목표로 한다.다양한 주파수와 진폭의 순수 주파수(사인파)를 합산하는 것으로, 만들고 싶은 소리의 음색을 정확하게 정의할 수 있습니다.
정의들
고조파 가법 합성은 주기 함수를 공통 기본 주파수의 정수 배수와 같은 주파수로 사인파 함수의 합으로 표현하는 방법인 푸리에 급수의 개념과 밀접하게 관련되어 있습니다.이러한 사인파는 고조파, 음색 또는 일반적으로 부분음이라고 불립니다.일반적으로 푸리에 시리즈는 사인파 함수의 주파수에 대한 상한 없이 무한히 많은 사인파 성분을 포함하고 있으며 DC 성분(주파수가 0Hz인 것)을 포함합니다.가산 합성에서는 인간의 가청 범위 밖의 주파수를 생략할 수 있다.그 결과 가청 범위 내에 있는 주파수의 유한한 수의 사인파 항만이 가산 합성으로 모델링된다.
파형 또는 함수는 다음과 같은 경우 주기적이라고 합니다.
모든 t에 대해 일정 기간 PP에 대해
주기 함수의 푸리에 급수는 수학적으로 다음과 같이 표현됩니다.
어디에
- 0 / {\}=는 파형의 기본 주파수이며 주기의 역수와 같습니다.
- 2}}}}은 k k)번째 의 진폭입니다.
- k ( ,){ \{k}=\k})는 {k}번째 고조파의 오프셋입니다.atan2는 4차원 아크탄젠트 함수입니다.
DC 컴포넌트인 2}/2 및 주파수가 유한한계보다 높은 모든 인 는 다음 추가 합성 표현에서 생략됩니다.
조화형
가장 간단한 고조파 가법 합성은 수학적으로 다음과 같이 표현될 수 있습니다.
-
(1)
서 y { y는 합성 출력, { f(\ 및 (\는 각각의 고조파 부분k의 진폭, 주파수 및 위상 오프셋입니다. K 고조파 부분 f 은 파형의 기본 주파수이며 음표의 주파수입니다.
시간 의존적 진폭
 | 각 고조파가 시간에 의존하는 진폭을 갖는 고조파 가법 합성의 예.기본 주파수는 440Hz입니다. |
보다 일반적으로 각 고조파의 진폭은 의 함수 k ( 로 규정할 수 있습니다.이 경우 합성 출력은 다음과 같습니다.
- (t ) ( ) cos ( f t + k) ( ( 2k f 0 t ) \ _ {=} _ { ( ) \ \ ( 2 \ pi _ { } + \ { } )
(2)
각 k( 는 인접한 사인파 사이의 주파수 간격에 따라 천천히 변화해야 합니다.k ( ){ r { } ( )의 대역폭은 f { style _ { }보다 크게 작아야 합니다.
부조화형
또한 가법 합성은 개별 함축이 공통 기본 [5][6]주파수의 정수 배수인 주파수를 가질 필요가 없는 비조화음(무주기 파형)을 생성할 수 있습니다.많은 전통적인 악기들이 조화 부분(예: 오보에)을 가지고 있는 반면, 어떤 악기들은 조화되지 않은 부분(예: 종)을 가지고 있다.부조화 첨가 합성은 다음과 같이 설명될 수 있다.
서 f k})는 k k의 주파수입니다.
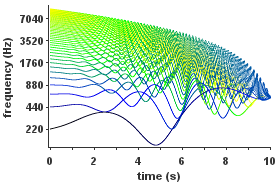 | 각 부분의 진폭과 주파수가 모두 시간에 의존하는 비조화 가법 합성의 예. |
시간 의존 주파수
일반적인 경우, 정현파의 순간 주파수는 사인 함수 또는 코사인 함수의 인수의 (시간에 관한) 도함수이다.이 주파수가 각 주파수 형식이 아닌 헤르츠로 표시되는 경우, 이 도함수는 \pi로 나눕니다.이것은 파셜이 고조파인지 부조화인지, 주파수가 일정한지 또는 시간 변동인지를 나타냅니다.
가장 일반적인 형태에서 각 비조화 파셜의 주파수는 시간의 음이 아닌 k ( 입니다.
-
(3)
폭넓은 정의
가법 합성은 단순한 요소를 합산하여 더 복잡한 음계를 만드는 음향 합성 기술을 의미할 수 있습니다. 요소가 사인파가 [7][8]아닐 때에도 마찬가지입니다.예를 들어 F입니다.리처드 무어는 가법 합성을 감산 합성, 비선형 합성, 물리적 [8]모델링과 함께 소리 합성의 "4가지 기본 범주" 중 하나로 열거했다.이 넓은 의미에서 파이프 오르간은 비 사인파 파형을 생성하는 파이프가 있으며, 가법 신시사이저의 변형 형태로 간주할 수 있습니다.주성분과 월시 함수의 합계는 또한 가법 [9]합성으로 분류되었다.
구현 방법
오늘날 적층 합성의 구현은 주로 디지털이다.(기본 이산 시간 이론은 섹션 이산 시간 방정식을 참조하십시오.)
발진기 뱅크 합성
가법 합성은 각 [1]부분마다 하나씩 정현파 발진기 뱅크를 사용하여 구현할 수 있습니다.
웨이브 테이블 합성
고조파, 준주기적인 음악 톤의 경우, 웨이브 테이블 합성은 시변하는 가법 합성만큼 일반적일 수 있지만,[10][11] 합성하는 동안 더 적은 계산이 필요하다.그 결과, 웨이브 테이블 합성을 이용하는 것으로, 고조파 톤의 시변 가산 합성의 효율적인 실장을 실현할 수 있다.
군첨가합성
그룹 가법[12][13][14] 합성은 파장을 조화 그룹(기본 주파수가 다름)으로 그룹화하고 결과를 혼합하기 전에 웨이브 테이블 합성으로 각 그룹을 개별적으로 합성하는 방법이다.
역FFT 합성
역고속 푸리에 변환은 변환 주기 또는 "프레임"을 균등하게 분할하는 주파수를 효율적으로 합성하는 데 사용할 수 있습니다.DFT 주파수 영역 표현을 신중하게 검토함으로써 일련의 겹치는 프레임과 역고속 푸리에 [15]변환을 사용하여 임의 주파수의 사인파를 효율적으로 합성할 수도 있다.
가법분석/재합성
녹음된 소리의 주파수 성분을 분석하여 "sum of sinsoids" 표현을 제공할 수 있습니다.이 표현은 가법 합성을 사용하여 재합성할 수 있습니다.음성을 시간 가변 사인파 파셜로 분해하는 방법 중 하나는 짧은 시간 푸리에 변환(STFT) 기반의 McAulay-Quatieri Analysis입니다.[17][18]
사인파 표현의 합을 수정함으로써 재합성 전에 추골 변화를 할 수 있다.예를 들어, 고조파 사운드를 비조화음으로 재구성할 수 있으며, 그 반대의 경우도 마찬가지입니다.음향 잡종화 또는 "모핑"은 가법 재합성에 [19]의해 구현되었다.
부가 분석/재합성 기능은 사인파 모델링,[20] 스펙트럼 모델링 합성(SMS)[19] 및 재할당 대역폭 확장 부가 사운드 [21]모델을 포함한 많은 기법에 채택되었다.가법 분석/재합성 구현 소프트웨어에는 SPEAR,[22] LEMUR, LORIS,[23] SMSTools,[24][25] ARSS가 포함됩니다.
상품들
New England Digital Synclavier는 샘플을 분석하여 가법 합성 엔진의 일부인 "음색 프레임"으로 변환할 수 있는 재합성 기능을 가지고 있었습니다.1987년에 출시된 Technos acxel은 FFT 구현에서 가법 분석/재합성 모델을 사용했다.
보컬로이드 첨가제 analysis/resynthesis의 기준에 적용된 또한 보컬 합성기이고: 더하여 그것의 스펙트럼 목소리 모델이라고 불리는 Excitation Resonances(EpR)model[26][27]스펙트럼 모델링의(SMS)에 의존해서는 diphoneconcatenative 합성 스펙트럼 첨두 처리(SICAF)[28]기법 유사한을 이용해 처리된다가 연장된다.수정하위상 잠금[29] 보코더(포름 처리용 [30]개량형 위상 보코더).이러한 기법을 사용하여 순수하게 고조파 파셜로 구성된 스펙트럼 성분(포름트)을 음향 모델링을 위해 원하는 형태로 적절히 변환할 수 있으며, 바람직한 문구를 구성하는 짧은 샘플(디폰 또는 음소)의 시퀀스는 각각 일치하는 파셜과 포름트 피크를 보간함으로써 매끄럽게 연결될 수 있다.서로 다른 검체 사이의 톱니형 전이 영역.('다이나믹 팀브레스'도 참조)
적용들
악기
가법 합성은 전자악기에 사용된다.그것은 저명한 기관이 사용하는 주요 소리 발생 기술이다.
음성 합성
언어학 연구에서는 1950년대에 변형된 합성 음성 스펙트럼을 [31]재생하기 위해 조화 가법 합성이 사용되었다.
이후 1980년대 초, 그 중요성을 평가하기 위해 음향 신호가 제거된 합성 음성에 대한 듣기 테스트가 수행되었다.선형 예측 부호화에 의해 도출된 시간 가변 공식 주파수 및 진폭은 순수한 톤 휘파람으로 부가적으로 합성되었다.이 방법을 사인파 [32][33]합성이라고 합니다.또한 야마하 CX5M(1984)의 가창 음성 합성 기능에 사용된 복합 사인파 모델링(CSM)[34][35]은 1966-1979년에 [36][37]독립적으로 개발된 유사한 접근방식을 사용하는 것으로 알려져 있다.이러한 방법은 음향의 관점에서 구강과 비강에서 발생한 몇 가지 공명 모드에 해당하는 일련의 유의한 스펙트럼 피크를 추출하고 재구성하는 것이 특징이다.이 원리는 모달 [38][39][40][41]합성이라고 불리는 물리적 모델링 합성 방법에도 사용되었습니다.
역사
고조파 분석은 [43]조셉 푸리에에 의해 발견되었는데,[42] 그는 1822년 열 전달의 맥락에서 그의 연구에 대한 광범위한 논문을 발표했다.그 이론은 조수의 예측에 조기에 적용되었다.1876년경,[44] 윌리엄 톰슨(나중에 켈빈 경으로 귀속됨)은 기계적인 조류 예측기를 만들었다.그것은 19세기에 [45][46]이미 불렸던 조화 분석기와 조화 신시사이저로 구성되었다.조류 측정 분석은 James Thomson의 통합 기계를 사용하여 수행되었습니다.결과 푸리에 계수는 신시사이저에 입력되었고, 신시사이저는 코드와 풀리 시스템을 사용하여 미래 조수의 예측을 위한 고조파 사인파 부분을 생성하고 합했다.1910년에 [47]소리의 주기적인 파형의 분석을 위해 비슷한 기계가 만들어졌다.신시사이저는 주로 [47]분석의 시각적 검증에 사용된 조합 파형의 그래프를 그렸다.
게오르크 옴은 1843년에 푸리에의 이론을 소리에 적용했다.헤르만 폰 헬름홀츠는 1863년 [48]8년간의 연구를 발표했다.헬름홀츠는 음색에 대한 심리적 지각은 학습의 대상인 반면, 감각적인 감각의 청각은 순전히 [49]생리적인 것이라고 믿었다.그는 소리의 지각이 기저막의 신경세포에서 나오는 신호에서 비롯되고 이러한 세포의 탄력적인 부속물이 적절한 [47]주파수의 순수한 사인파 톤에 의해 교감적으로 진동한다는 생각을 지지했다.헬름홀츠는 1787년 에른스트 클라드니가 특정 음원이 부조화 진동 [49]모드를 가지고 있다는 발견에 동의했습니다.
헬름홀츠 시대에는 전자 증폭을 사용할 수 없었습니다.고조파 파셜을 가진 톤의 합성을 위해 헬름홀츠는 파셜의 [50]진폭을 조정할 수 있는 튜닝 포크와 음향 공명 챔버의 전기적으로 흥분된 어레이를 구축했습니다.적어도 [50]1862년에 지어진 이 건물들은 [50]1872년에 자신의 구성을 보여준 루돌프 코닉에 의해 다듬어졌다.조화 합성을 위해, Koenig는 또한 그의 파도 사이렌을 바탕으로 큰 장치를 만들었습니다.공압식이며 컷아웃된 톤휠을 사용했으며 부분 [44]톤의 순도가 낮다는 비판을 받았다.또한 파이프 기관의 경골관은 거의 정현파 파형을 가지며, 가법 [44]합성 방식으로 조합할 수 있다.
1938년, 중요한 새로운 [51]증거와 함께, 인간의 성대는 조화로운 소리를 내기 위해 불 사이렌과 같은 기능을 하고, 그리고 나서 다른 [52]모음 소리를 내기 위해 성관에 의해 걸러진다는 것이 Popular Science Monthly의 페이지에 보고되었습니다.그 무렵에는 첨가물인 해먼드 오르간은 이미 시장에 나와 있었다.대부분의 초기 전자 오르간 제조업체들은 첨가 기관에 필요한 여러 발진기를 제작하는 것이 너무 비싸다고 생각했고, 대신 감산기를 [53]제작하기 시작했습니다.1940년 라디오 엔지니어 협회에서 Hammond의 수석 현장 엔지니어는 회사의 새로운 [54]Novachord가 "음파를 결합하여 최종 음색을 만들어 내는" 원래의 Hammond 오르간과는 대조적으로 "추상적인 시스템"을 가지고 있다고 상세히 설명했습니다.앨런 더글라스는 1948년 왕립음악협회에 [55]제출된 논문에서 다른 종류의 전자 오르간을 설명하기 위해 가감수자를 사용했다.현대적 단어 첨가 합성과 감산 합성은 그의 1957년 저서 "음악의 전기적 생산"에서 찾을 수 있는데, 이 책에서 그는 가법 합성, 감산 합성, 그리고 기타 형태의 [56]조합이라는 섹션에서 음악 음색을 형성하는 세 가지 방법을 범주적으로 열거한다.
일반적인 현대식 가법 신시사이저는 2000년경 [57]인기를 끌었던 소프트웨어 신시사이저의 경우처럼 전기, 아날로그 신호 또는 디지털 오디오로 출력을 생성합니다.
타임라인
다음은 역사적으로나 기술적으로 주목할 만한 아날로그 및 디지털 신시사이저와 가법 합성을 구현하는 장치의 연대표입니다.
| 연구실시 또는 간행물 | 시판 중 | 회사 또는 기관 | 신시사이저 또는 합성 장치 | 묘사 | 오디오 샘플 |
|---|---|---|---|---|---|
| 1900년[58] | 1906년[58] | 뉴잉글랜드 일렉트릭 뮤직 컴퍼니 | 텔하모늄 | 최초의 다성 음악 신시사이저, 터치 감응형 음악 신시사이저.[59]톤휠과 교류발전기를 이용한 신오소이드 적층합성 구현.Thaddeus Cahill에 의해 발명되었습니다. | 알려진 녹음 없음[58] |
| 1933년[60] | 1935년[60] | 해먼드 오르간 컴퍼니 | 해먼드 오르간 | 텔하모늄보다 [59]상업적으로 더 성공한 전자 첨가 신시사이저입니다.톤휠 및 자기 픽업을 사용한 사인파 가법 합성 구현.로렌스 해먼드에 의해 발명되었다. | |
| 1950년 이전[31] | 하스킨스 연구소 | 패턴 재생 | 손으로 그린 스펙트로그램이나 분석 결과에 의해 고조파 편성의 진폭을 제어하는 음성 합성 시스템.파셜은 멀티트랙 광학 [31]톤휠에 의해 생성되었습니다. | 샘플 | |
| 1958년[61] | ANS | 멀티트랙 광학 톤휠을 사용하여 마이크로톤 스펙트로그램과 같은 악보를 재생한 가법[62] 신시사이저입니다.Evgeny Murzin에 의해 발명되었습니다.전자 발진기, 발진기 뱅크와 그 입력 장치 스펙트로그램을 이용한 유사한 기구는 [63][64]1959년 휴 르 케인에 의해 실현되었다. | |||
| 1963년[65] | MIT | David [65]Luce에 의한 공격과 정상 상태 부분의 디지털 스펙트럼 분석 및 재합성용 오프라인 시스템입니다. | |||
| 1964년[66] | 일리노이 대학교 | 고조파 톤 발생기 | James Beauchamp에 [66][67]의해 발명된 전자적, 조화적 첨가 합성 시스템. | 샘플(info) | |
| 1974년 이전[68][69] | 1974년[68][69] | RMI | 고조파 신시사이저 | 디지털 [68][69]발진기를 이용한 적층 합성을 구현한[70] 최초의 신시사이저 제품.신시사이저에는 시시각각 변하는 아날로그 [68]필터도 있었다.RMI는 1971년 북미 [71]록웰이 개발한 디지털 기술을 사용하여 최초의 상업용 디지털 교회 오르간인 앨런 컴퓨터 오르간을 발매한 앨런 오르간 회사의 자회사였다. | 1 2 3 4 |
| 1974년[72] | EMS(런던) | 디지털 발진기 뱅크 | 임의 파형, 개별 주파수 및 진폭 [73]제어를 갖춘 디지털 발진기의 뱅크.[72][73] EMS에서 구축된 디지털 분석 필터 뱅크(AFB)와 함께 분석-재합성에도 사용됩니다. DOB라고도 합니다. | 새로운 사운드 오브[74] 뮤직 | |
| 1976년[75] | 1976년[76] | 페어라이트 | 카사르 M8 | 고속 푸리에[77] 변환을 사용하여 대화식으로 그려진 고조파 [78]진폭 엔벨로프로부터 샘플을 생성하는 전체 디지털 신시사이저입니다. | 샘플 |
| 1977년[79] | 벨 연구소 | 디지털 신시사이저 | 최초의 진정한 디지털 [80]신시사이저라고 불리는 실시간 디지털 가법[79] 신시사이저.일명 앨리스 머신, 앨리스. | 샘플(info) | |
| 1979년[80] | 1979년[80] | 뉴잉글랜드 디지털 | 싱클레이비어 II | 적층 합성에 의해 생성된 파형 간의 부드러운 크로스페이드로 시간 경과에 따른 음색 개발을 가능하게 한 상용 디지털 신시사이저입니다. |
이산 시간 방정식
가산합성 디지털 구현에서는 연속시간 합성방정식 대신 이산시간방정식이 사용된다. 시간 신호의 표기 규칙에서는 y[{ y {n} 등의 괄호를 사용하며 n { n은 정수 값만 사용할 수 있습니다.연속시간 y { y {의 절반 인 충분한 대역제한이 예상되는 경우 연속시간 식을 직접 샘플링하여 이산합성식을 구하면 된다.연속 합성 출력은 나중에 디지털-아날로그 변환기를 사용하여 샘플에서 재구성할 수 있습니다.샘플링 주기는 T / s {\ T입니다.
(3)부터 시작해서
그리고 이산 / s { t == n/{s}},}의 샘플링 결과는 다음과 같습니다.
어디에
- k[ ] k ( T ]=는 이산 시간 가변 진폭 엔벨로프입니다.
- _는 이산 시간 역차 순간 주파수입니다.
이것은 에 상당합니다.
어디에
- θ k[n]=2π fs∑ 나는 갈1nf[나는]+ϕ k=θ k[n− 1]+2π fsfk[n]{\displaystyle{\begin{정렬}\theta _ᆱ[n]&, ={\frac{2\pi}{f_{\mathrm{s}}}}\sum _ᆴ^ᆵf_ᆶ[나는]+\phi _{k}\\&, =\theta _ᆸ[n-1]+{\frac{2\pi}{f_{\mathrm{s}}}}f_ᆻ[n]\\\end{alignk.교육}}} n> { n > 0 ,} 。
그리고.
「 」를 참조해 주세요.
레퍼런스
- ^ a b Julius O. Smith III. "Additive Synthesis (Early Sinusoidal Modeling)". Retrieved 14 January 2012.
The term "additive synthesis" refers to sound being formed by adding together many sinusoidal components
- ^ Gordon Reid. "Synth Secrets, Part 14: An Introduction To Additive Synthesis". Sound on Sound (January 2000). Retrieved 14 January 2012.
- ^ Mottola, Liutaio (31 May 2017). "Table of Musical Notes and Their Frequencies and Wavelengths".
- ^ "Fundamental Frequency and Harmonics".
- ^ 스미스 3세, 줄리어스 O;세라, 사비에르(2005년)."애디 티브 종합".PARSHL:Analysis/Synthesis 프로그램 Non-Harmonic 소리에 대한 관하표현에 기초를 둔다.국제 컴퓨터 음악 회의(ICMC-87, 도쿄), 컴퓨터 음악 협회, 1987년의 논문집.CCRMA, 음악, 스탠포드 대학교입니다.1월 11일 2015년.(온라인 추가 인화하다)Retrieved.
- ^ Smith III, Julius O. (2011). "Additive Synthesis (Early Sinusoidal Modeling)". Spectral Audio Signal Processing. CCRMA, Department of Music, Stanford University. ISBN 978-0-9745607-3-1. Retrieved 9 January 2012.
- ^ Roads, Curtis (1995). The Computer Music Tutorial. MIT Press. p. 134. ISBN 978-0-262-68082-0.
- ^ a b Moore, F. Richard (1995). Foundations of Computer Music. Prentice Hall. p. 16. ISBN 978-0-262-68082-0.
- ^ Roads, Curtis (1995). The Computer Music Tutorial. MIT Press. pp. 150–153. ISBN 978-0-262-68082-0.
- ^ Robert Bristow-Johnson (November 1996). "Wavetable Synthesis 101, A Fundamental Perspective" (PDF). Archived from the original (PDF) on 15 June 2013. Retrieved 21 May 2005.
- ^ Andrew Horner (November 1995). "Wavetable Matching Synthesis of Dynamic Instruments with Genetic Algorithms". Journal of the Audio Engineering Society. 43 (11): 916–931.
- ^ Julius O. Smith III. "Group Additive Synthesis". CCRMA, Stanford University. Archived from the original on 6 June 2011. Retrieved 12 May 2011.
- ^ P. Kleczkowski (1989). "Group additive synthesis". Computer Music Journal. 13 (1): 12–20. doi:10.2307/3679851. JSTOR 3679851.
- ^ B. Eaglestone and S. Oates (1990). "Analytical tools for group additive synthesis". Proceedings of the 1990 International Computer Music Conference, Glasgow. Computer Music Association.
- ^ a b Rodet, X.; Depalle, P. (1992). "Spectral Envelopes and Inverse FFT Synthesis". Proceedings of the 93rd Audio Engineering Society Convention. CiteSeerX 10.1.1.43.4818.
- ^ McAulay, R. J.; Quatieri, T. F. (1988). "Speech Processing Based on a Sinusoidal Model" (PDF). The Lincoln Laboratory Journal. 1 (2): 153–167. Archived from the original (PDF) on 21 May 2012. Retrieved 9 December 2013.
- ^ McAulay, R. J.; Quatieri, T. F. (August 1986). "Speech analysis/synthesis based on a sinusoidal representation". IEEE Transactions on Acoustics, Speech, Signal Processing ASSP-34. 34 (4): 744–754. doi:10.1109/TASSP.1986.1164910.
- ^ "McAulay-Quatieri Method".
- ^ a b Serra, Xavier (1989). A System for Sound Analysis/Transformation/Synthesis based on a Deterministic plus Stochastic Decomposition (PhD thesis). Stanford University. Retrieved 13 January 2012.
- ^ Smith III, Julius O.; Serra, Xavier. "PARSHL: An Analysis/Synthesis Program for Non-Harmonic Sounds Based on a Sinusoidal Representation". Retrieved 9 January 2012.
- ^ Fitz, Kelly (1999). The Reassigned Bandwidth-Enhanced Method of Additive Synthesis (PhD thesis). Dept. of Electrical and Computer Engineering, University of Illinois Urbana-Champaign. CiteSeerX 10.1.1.10.1130.
- ^ SPEAR 사인파 부분 편집 분석 및 Mac OS X, Mac OS 9 및 Windows용 재합성
- ^ "Loris Software for Sound Modeling, Morphing, and Manipulation". Archived from the original on 30 July 2012. Retrieved 13 January 2012.
- ^ Windows용 SMSTools 응용 프로그램
- ^ ARSS: 분석 및 재합성 사운드 스펙트로그래프
- ^ Bonada, J.; Celma, O.; Loscos, A.; Ortola, J.; Serra, X.; Yoshioka, Y.; Kayama, H.; Hisaminato, Y.; Kenmochi, H. (2001). "Singing voice synthesis combining Excitation plus Resonance and Sinusoidal plus Residual Models". Proc. Of ICMC. CiteSeerX 10.1.1.18.6258. (PDF)
- ^ Loscos, A. (2007). Spectral processing of the singing voice (PhD thesis). Barcelona, Spain: Pompeu Fabra University. hdl:10803/7542. (PDF).
"흥분 + 공명 음성 모델" (p.51)을 참조하십시오. - ^ Loscos 2007, 페이지 44, "스펙트럼 피크 처리"
- ^ Loscos 2007, 페이지 44, "위상 잠금 보코더"
- ^ Bonada, Jordi; Loscos, Alex (2003). "Sample-based singing voice synthesizer by spectral concatenation: 6. Concatenating Samples". Proc. of SMAC 03: 439–442.
- ^ a b c Cooper, F. S.; Liberman, A. M.; Borst, J. M. (May 1951). "The interconversion of audible and visible patterns as a basis for research in the perception of speech". Proc. Natl. Acad. Sci. U.S.A. 37 (5): 318–25. Bibcode:1951PNAS...37..318C. doi:10.1073/pnas.37.5.318. PMC 1063363. PMID 14834156.
- ^ Remez, R.E.; Rubin, P.E.; Pisoni, D.B.; Carrell, T.D. (1981). "Speech perception without traditional speech cues". Science. 212 (4497): 947–950. Bibcode:1981Sci...212..947R. doi:10.1126/science.7233191. PMID 7233191. S2CID 13039853.
- ^ Rubin, P.E. (1980). "Sinewave Synthesis Instruction Manual (VAX)" (PDF). Internal Memorandum. Haskins Laboratories, New Haven, CT.
- ^ Sagayama, S.; Itakura, F. (1979), "複合正弦波による音声合成" [Speech Synthesis by Composite Sinusoidal Wave], Speech Committee of Acoustical Society of Japan (published October 1979), S79-39
- ^ Sagayama, S.; Itakura, F. (1979), "複合正弦波による簡易な音声合成法" [Simple Speech Synthesis method by Composite Sinusoidal Wave], Proceedings of Acoustical Society of Japan, Autumn Meeting (published October 1979), vol. 3-2-3, pp. 557–558
- ^ Sagayama, S.; Itakura, F. (1986). "Duality theory of composite sinusoidal modeling and linear prediction". ICASSP '86. IEEE International Conference on Acoustics, Speech, and Signal Processing. Acoustics, Speech, and Signal Processing, IEEE International Conference on ICASSP '86. Vol. 11 (published April 1986). pp. 1261–1264. doi:10.1109/ICASSP.1986.1168815. S2CID 122814777.
- ^ Itakura, F. (2004). "Linear Statistical Modeling of Speech and its Applications -- Over 36-year history of LPC --" (PDF). Proceedings of the 18th International Congress on Acoustics (ICA 2004), We3.D, Kyoto, Japan, Apr. 2004. (published April 2004). 3: III–2077–2082.
6. Composite Sinusoidal Modeling(CSM) In 1975, Itakura proposed the line spectrum representation (LSR) concept and its algorithm to obtain a set of parameters for new speech spectrum representation. Independently from this, Sagayama developed a composite sinusoidal modeling (CSM) concept which is equivalent to LSR but give a quite different formulation, solving algorithm and synthesis scheme. Sagayama clarified the duality of LPC and CSM and provided the unified view covering LPC, PARCOR, LSR, LSP and CSM, CSM is not only a new concept of speech spectrum analysis but also a key idea to understand the linear prediction from a unified point of view. ...
- ^ Adrien, Jean-Marie (1991). "The missing link: modal synthesis". In Giovanni de Poli; Aldo Piccialli; Curtis Roads (eds.). Representations of Musical Signals. Cambridge, MA: MIT Press. pp. 269–298. ISBN 978-0-262-04113-3.
- ^ Morrison, Joseph Derek (IRCAM); Adrien, Jean-Marie (1993). "MOSAIC: A Framework for Modal Synthesis". Computer Music Journal. 17 (1): 45–56. doi:10.2307/3680569. JSTOR 3680569.
- ^ 빌바오, 스테판(2009년 10월),"모드 종합", 수치 해석적 사운드의:.유한 차분법 주체 및 시뮬레이션 뮤지컬 음향, 치체스터 경은 영국:JohnWiley도와 Sons, 아이 에스비엔 978-0-470-51046-9, 다른 접근, 축소 모형 실험 사운드 합성에 오랜 역사와 잠재적으로 복잡한 기하학의 개체의 진동은 frequency-domain, 또는 모델 설명에 근거한다.에서 진동하는 물건의 복잡한 동적 행동 모드(손에 그 특정한 문제의 공간 형태가 있eigenfunctions고 경계 조건에 따라 달라진다)의는 하나의 복잡한 freque에 oscillates 세트로부터 공헌들로 분해할 수 있Modal 합성[1,148],는, 호소하고 있다.Ncy....(또한 동반자 페이지를 참조하십시오).
- ^ Doel, Kees van den; Pai, Dinesh K. (2003). Greenebaum, K. (ed.). "Modal Synthesis For Vibrating Object" (PDF). Audio Anecdotes. Natick, MA: AK Peter.
When a solid object is struck, scraped, or engages in other external interactions, the forces at the contact point causes deformations to propagate through the body, causing its outer surfaces to vibrate and emit sound waves. ... A good physically motivated synthesis model for objects like this is modal synthesis ... where a vibrating object is modeled by a bank of damped harmonic oscillators which are excited by an external stimulus.
- ^ Prestini, Elena (2004) [Rev. ed of: Applicazioni dell'analisi armonica. Milan: Ulrico Hoepli, 1996]. The Evolution of Applied Harmonic Analysis: Models of the Real World. trans. New York, USA: Birkhäuser Boston. pp. 114–115. ISBN 978-0-8176-4125-2. Retrieved 6 February 2012.
- ^ Fourier, Jean Baptiste Joseph (1822). Théorie analytique de la chaleur [The Analytical Theory of Heat] (in French). Paris, France: Chez Firmin Didot, père et fils.
- ^ a b c Miller, Dayton Clarence (1926) [First published 1916]. The Science of Musical Sounds. New York: The Macmillan Company. pp. 110, 244–248.
- ^ The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. Taylor & Francis. 49: 490. 1875.
{{cite journal}}: CS1 유지보수 : 제목 없는 정기 (링크) - ^ Thomson, Sir W. (1878). "Harmonic analyzer". Proceedings of the Royal Society of London. Taylor and Francis. 27 (185–189): 371–373. doi:10.1098/rspl.1878.0062. JSTOR 113690.
- ^ a b c Cahan, David (1993). Cahan, David (ed.). Hermann von Helmholtz and the foundations of nineteenth-century science. Berkeley and Los Angeles, USA: University of California Press. pp. 110–114, 285–286. ISBN 978-0-520-08334-9.
- ^ Helmholtz, von, Hermann (1863). Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik [On the sensations of tone as a physiological basis for the theory of music] (in German) (1st ed.). Leipzig: Leopold Voss. pp. v.
- ^ a b Christensen, Thomas Street (2002). The Cambridge History of Western Music. Cambridge, United Kingdom: Cambridge University Press. pp. 251, 258. ISBN 978-0-521-62371-1.
- ^ a b c von Helmholtz, Hermann (1875). On the sensations of tone as a physiological basis for the theory of music. London, United Kingdom: Longmans, Green, and co. pp. xii, 175–179.
- ^ Russell, George Oscar (1936). Year book - Carnegie Institution of Washington (1936). Carnegie Institution of Washington: Year Book. Vol. 35. Washington: Carnegie Institution of Washington. pp. 359–363.
- ^ Lodge, John E. (April 1938). Brown, Raymond J. (ed.). "Odd Laboratory Tests Show Us How We Speak: Using X Rays, Fast Movie Cameras, and Cathode-Ray Tubes, Scientists Are Learning New Facts About the Human Voice and Developing Teaching Methods To Make Us Better Talkers". Popular Science Monthly. New York, USA: Popular Science Publishing. 132 (4): 32–33.
- ^ Comerford, P. (1993). "Simulating an Organ with Additive Synthesis". Computer Music Journal. 17 (2): 55–65. doi:10.2307/3680869. JSTOR 3680869.
- ^ "Institute News and Radio Notes". Proceedings of the IRE. 28 (10): 487–494. 1940. doi:10.1109/JRPROC.1940.228904.
- ^ Douglas, A. (1948). "Electrotonic Music". Proceedings of the Royal Musical Association. 75: 1–12. doi:10.1093/jrma/75.1.1.
- ^ Douglas, Alan Lockhart Monteith (1957). The Electrical Production of Music. London, UK: Macdonald. pp. 140, 142.
- ^ Pejrolo, Andrea; DeRosa, Rich (2007). Acoustic and MIDI orchestration for the contemporary composer. Oxford, UK: Elsevier. pp. 53–54.
- ^ a b c Weidenaar, Reynold (1995). Magic Music from the Telharmonium. Lanham, MD: Scarecrow Press. ISBN 978-0-8108-2692-2.
- ^ a b Moog, Robert A. (October–November 1977). "Electronic Music". Journal of the Audio Engineering Society. 25 (10/11): 856.
- ^ a b Olsen, Harvey (14 December 2011). Brown, Darren T. (ed.). "Leslie Speakers and Hammond organs: Rumors, Myths, Facts, and Lore". The Hammond Zone. Hammond Organ in the U.K. Archived from the original on 1 September 2012. Retrieved 20 January 2012.
- ^ Holzer, Derek (22 February 2010). "A brief history of optical synthesis". Retrieved 13 January 2012.
- ^ Vail, Mark (1 November 2002). "Eugeniy Murzin's ANS – Additive Russian synthesizer". Keyboard Magazine. p. 120.
- ^ Young, Gayle. "Oscillator Bank (1959)".
- ^ Young, Gayle. "Spectrogram (1959)".
- ^ a b Luce, David Alan (1963). Physical correlates of nonpercussive musical instrument tones (Thesis). Cambridge, Massachusetts, U.S.A.: Massachusetts Institute of Technology. hdl:1721.1/27450.
- ^ a b Beauchamp, James (17 November 2009). "The Harmonic Tone Generator: One of the First Analog Voltage-Controlled Synthesizers". Prof. James W. Beauchamp Home Page.
- ^ Beauchamp, James W. (October 1966). "Additive Synthesis of Harmonic Musical Tones". Journal of the Audio Engineering Society. 14 (4): 332–342.
- ^ a b c d "RMI Harmonic Synthesizer". Synthmuseum.com. Archived from the original on 9 June 2011. Retrieved 12 May 2011.
- ^ a b c Reid, Gordon. "PROG SPAWN! The Rise And Fall of Rocky Mount Instruments (Retro)". Sound on Sound (December 2001). Archived from the original on 25 December 2011. Retrieved 22 January 2012.
- ^ Flint, Tom. "Jean Michel Jarre: 30 Years of Oxygene". Sound on Sound (February 2008). Retrieved 22 January 2012.
- ^ "Allen Organ Company". fundinguniverse.com.
- ^ a b Cosimi, Enrico (20 May 2009). "EMS Story - Prima Parte" [EMS Story - Part One]. Audio Accordo.it (in Italian). Archived from the original on 22 May 2009. Retrieved 21 January 2012.
- ^ a b Hinton, Graham (2002). "EMS: The Inside Story". Electronic Music Studios (Cornwall). Archived from the original on 21 May 2013.
- ^ The New Sound of Music (TV). UK: BBC. 1979. DOB 및 AFB의 데모를 포함합니다.
- ^ Leete, Norm. "Fairlight Computer – Musical Instrument (Retro)". Sound on Sound (April 1999). Retrieved 29 January 2012.
- ^ Twyman, John (1 November 2004). (inter)facing the music: The history of the Fairlight Computer Musical Instrument (PDF) (Bachelor of Science (Honours) thesis). Unit for the History and Philosophy of Science, University of Sydney. Retrieved 29 January 2012.
- ^ Street, Rita (8 November 2000). "Fairlight: A 25-year long fairytale". Audio Media magazine. IMAS Publishing UK. Archived from the original on 8 October 2003. Retrieved 29 January 2012.
- ^ "Computer Music Journal" (JPG). 1978. Retrieved 29 January 2012.
- ^ a b Leider, Colby (2004). "The Development of the Modern DAW". Digital Audio Workstation. McGraw-Hill. p. 58.
- ^ a b c Joel, Chadabe (1997). Electric Sound. Upper Saddle River, N.J., U.S.A.: Prentice Hall. pp. 177–178, 186. ISBN 978-0-13-303231-4.







![{\begin{aligned}y(t)&={\frac {a_{0}}{2}}+\sum _{k=1}^{\infty }\left[a_{k}\cos(2\pi kf_{0}t)-b_{k}\sin(2\pi kf_{0}t)\right]\\&={\frac {a_{0}}{2}}+\sum _{k=1}^{\infty }r_{k}\cos \left(2\pi kf_{0}t+\phi _{k}\right)\\\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/522ace082a6d8990934113a639987f09a885cf02)
 파형의
파형의 







 합성 출력,
합성 출력, 


 파형의
파형의 

 인접한 사인파 사이의 주파수 간격에 따라 천천히 변화해야 합니다.
인접한 사인파 사이의 주파수 간격에 따라 천천히 변화해야 합니다.












![y[n]\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/e73a8042c0d1a4c5d264982972d2ef33eda55e34)
 정수 값만 사용할 수 있습니다.연속시간
정수 값만 사용할 수 있습니다.연속시간 




![{\begin{aligned}y[n]&=y(nT)=\sum _{k=1}^{K}r_{k}(nT)\cos \left(2\pi \int _{0}^{nT}f_{k}(u)\ du+\phi _{k}\right)\\&=\sum _{k=1}^{K}r_{k}(nT)\cos \left(2\pi \sum _{i=1}^{n}\int _{(i-1)T}^{iT}f_{k}(u)\ du+\phi _{k}\right)\\&=\sum _{k=1}^{K}r_{k}(nT)\cos \left(2\pi \sum _{i=1}^{n}(Tf_{k}[i])+\phi _{k}\right)\\&=\sum _{k=1}^{K}r_{k}[n]\cos \left({\frac {2\pi }{f_{\mathrm {s} }}}\sum _{i=1}^{n}f_{k}[i]+\phi _{k}\right)\\\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/235e423ed6dcd7564ba02d91eee3b6a012e84ce4)
![r_{k}[n]=r_{k}(nT)\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a91ccc3b0935394fad361cdc119c27a51b0c278) 이산 시간 가변 진폭 엔벨로프입니다.
이산 시간 가변 진폭 엔벨로프입니다.![f_{k}[n]={\frac {1}{T}}\int _{(n-1)T}^{nT}f_{k}(t)\ dt\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/1043b3eaee212fedc8c9c8d408aad44dce3c4af1) 이산
이산 ![y[n]=\sum _{k=1}^{K}r_{k}[n]\cos \left(\theta _{k}[n]\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbce88acb5e1e6a4ef32dd0be9bd49b78325a7de)
![\theta _{k}[0]=\phi _{k}.\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea1d7745c11e8890b24efb6c72f8c5a320d8b27e)


