물리과학에서 에어리 함수 (또는 제1종류의 에어리 함수 ) 아이(x ) 영국 의 천문학자 조지 비델 에어리 (1801–1892)의 이름을 딴 특수 함수 다. Ai(x ) 와 관련 함수 Bi(x ) 미분 방정식 에 대한 선형 독립 솔루션이다.
d 2 y d x 2 − x y = 0 , {\displaystyle {\frac {d^{2}y}{dx^{2}}-xy=0,} 에어리 방정식 또는 스톡스 방정식 으로 알려져 있다.이것은 전환점(솔루션의 특성이 진동에서 지수적으로 변하는 지점)을 가진 가장 단순한 2차 선형 미분 방정식 이다.[citation needed
정의들 x 의 실제 값에 대해 첫 번째 종류의 에어리 함수는 부적절 한 리만 적분 으로 정의할 수 있다.
아이 ( x ) = 1 π ∫ 0 ∞ cas ( t 3 3 + x t ) d t ≡ 1 π 임이 있는 b → ∞ ∫ 0 b cas ( t 3 3 + x t ) d t , {\displaystyle \operatorname {Ai} (x)={\dfrac {1}{\pi }}\int _{0}^{\infty }\cos \left({\dfrac {t^{3}}{3}}+xt\right)\,dt\equiv {\dfrac {1}{\pi }}\lim _{b\to \infty }\int _{0}^{b}\cos \left({\dfrac {t^{3}}{3}}+xt\right)\,dt,} 디리클레의 테스트 에 의해 수렴되는 거야실제 {\displaystyle x } 3 x {\textstyle {\dfrac{t^{3}}{3}+xt} M ∞ ){\displaystystyle [M,\inforty )} 번호 {\ 대체 x t {\textstyle u={\dfrac{t^{3}}{3 }}+xt} .
y Ai(x ) 가 에어리 방정식을 만족함
이 방정식은 두 개의 선형 독립 해법이 있다. 스칼라 곱셈까지, ai(x ) 는 y 0 ∞ 조건의 대상 솔루션이다. 다른 솔루션에 대한 표준 선택은 Bi(x )로 표시된 두 번째 종류의 에어리 기능이다. 진동의 진폭이 Ai(x ) 와 x → π /2
비 ( x ) = 1 π ∫ 0 ∞ [ 생략하다 ( − t 3 3 + x t ) + 죄를 짓다 ( t 3 3 + x t ) ] d t . {\displaystyle \operatorname {Bi} (x)={\frac {1}{\pi }}\int _{0}^{\infty }\left[\exp \left(-{\tfrac {t^{3}}{3}}+xt\right)+\sin \left({\tfrac {t^{3}}{3}}+xt\right)\,\right]dt.}
특성. ai(x ) 와 Bi(x ) 의 값과 x 0 에서의 파생상품은 다음과 같다.
아이 ( 0 ) = 1 3 2 3 Γ ( 2 3 ) , 아이 ′ ( 0 ) = − 1 3 1 3 Γ ( 1 3 ) , 비 ( 0 ) = 1 3 1 6 Γ ( 2 3 ) , 비 ′ ( 0 ) = 3 1 6 Γ ( 1 3 ) . {\displaystyle{\begin{정렬}\operatorname{아이}(0)&,{}={\frac{1}{3^{\frac{2}{3}}\Gamma({\tfrac{2}{3}})}},&,\quad\operatorname{아이}'(0)&,{}=-{\frac{1}{3^{\frac{1}{3}}\Gamma({\tfrac{1}{3}})}},\\\operatorname{비}(0)&,{}={\frac{1}{3^{\frac{1}{6}}\Gamma({\tfrac{2}{3}})}},&,\quad\operatorname{비}'(0)&,{}={\frac{3^.{\frac{1}{6}}}{\Gamma( {\tfrac {1}{3}}}}. \end{정렬}}} 여기서 γ 은 감마 함수 를 나타낸다. 이어 아이(x ) 와 비(x ) 의 룬스키안 이 1/10 이라는 것이다.
x 가 양수일 때 Ai(x ) 는 양수, 볼록 , 0으로 기하급수적으로 감소하는 반면, Bi(x ) 는 양수, 볼록, 기하급수적으로 증가한다.x 가 음수일 때, Ai(x ) 와 Bi(x ) 는 계속 증가하는 주파수와 계속 감소하는 진폭으로 0 주위에 진동한다.이것은 에어리 기능에 대한 아래의 점근성 공식에 의해 지지된다.
에어리 함수는 직교함수로서[1]
∫ − ∞ ∞ 아이 ( t + x ) 아이 ( t + y ) d t = δ ( x − y ) {\displaystyle \int _{-\infit }^{\infit }\operatorname {Ai}(t+x)\operatorname {Ai}(t+y)dt=\delta(x-y)} 부적절한 Riemann 적분 사용.
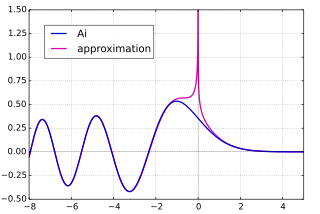
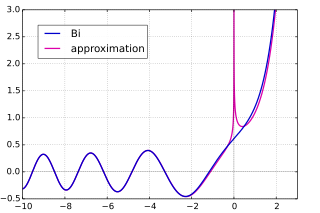
점근성공식 Ai(파란색) 및 사인파/외전증 무증상 형태의 Ai(마젠타) Bi(파란색) 및 사인파/외부 점증적 형태의 Bi(마젠타) 아래에서 설명한 것처럼 에어리 기능은 복잡한 평면으로 확장되어 전체 기능 을 제공할 수 있다. z 가 arg (z ) arg(z ): 이것을 stokes 현상 이라고 한다.arg(z ) π Ai(z )에 대해 다음과 같은 점증식 공식 을 가지고 있다. [2]
아이 ( z ) ∼ e − 2 3 z 3 2 2 π z 1 4 [ ∑ n = 0 ∞ ( − 1 ) n Γ ( n + 5 6 ) Γ ( n + 1 6 ) ( 3 4 ) n 2 π n ! z 3 n / 2 ] . {\displaystyle \operatorname {Ai} (z)\sim {\dfrac {e^{-{\frac {2}{3}}z^{\frac {3}{2}}}}{2{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (n+{\frac {5}{6}}) \감마(n+{\frac {1}{6})\왼쪽({\frac {3}{4}}\오른쪽) ^{n}}{2\pi n!z^{3n/2}}\오른쪽]. } 그리고 Bi(z )에도 유사한 것이 있지만, arg(z ) π /3
비 ( z ) ∼ e 2 3 z 3 2 π z 1 4 [ ∑ n = 0 ∞ Γ ( n + 5 6 ) Γ ( n + 1 6 ) ( 3 4 ) n 2 π n ! z 3 n / 2 ] . {\displaystyle \operatorname {Bi} (z)\sim {\frac {e^{{\frac {2}{3}}z^{\frac {3}{2}}}}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {\Gamma (n+{\frac {5}{6}}) \감마(n+{\frac {1}{6})\왼쪽({\frac {3}{4}}\오른쪽) ^{n}}{2\pi n!z^{3n/2}}\오른쪽]. }
π /3 (z ) Ai( z ) 에 대해 보다 정확한 공식과 Bi(z) 에 대해 동등하게, arg(z ) )/3일 때 Bi (-z ) 에 대해서는 0이 아니라 다음과 같은 공식이다.[2] [3]
아이 ( − z ) ∼ 죄를 짓다 ( 2 3 z 3 2 + π 4 ) π z 1 4 [ ∑ n = 0 ∞ ( − 1 ) n Γ ( 2 n + 5 6 ) Γ ( 2 n + 1 6 ) ( 3 4 ) 2 n 2 π ( 2 n ) ! z 3 n ] − cas ( 2 3 z 3 2 + π 4 ) π z 1 4 [ ∑ n = 0 ∞ ( − 1 ) n Γ ( 2 n + 11 6 ) Γ ( 2 n + 7 6 ) ( 3 4 ) 2 n + 1 2 π ( 2 n + 1 ) ! z 3 n + 3 / 2 ] 비 ( − z ) ∼ cas ( 2 3 z 3 2 + π 4 ) π z 1 4 [ ∑ n = 0 ∞ ( − 1 ) n Γ ( 2 n + 5 6 ) Γ ( 2 n + 1 6 ) ( 3 4 ) 2 n 2 π ( 2 n ) ! z 3 n ] + 죄를 짓다 ( 2 3 z 3 2 + π 4 ) π z 1 4 [ ∑ n = 0 ∞ ( − 1 ) n Γ ( 2 n + 11 6 ) Γ ( 2 n + 7 6 ) ( 3 4 ) 2 n + 1 2 π ( 2 n + 1 ) ! z 3 n + 3 / 2 ] . {\displaystyle {\begin}\operatorname {Ai}(-z)\sim &}{}{\frac {2}{3}z^{3}{3}}{2}}{\frac {\frac {}}}{4}}\right) }}{{\sqrt{\pi}}\z^{1}{1}}}\왼쪽[\sum _{n=0}^{\inflt }{\dfrac {(-1)^{n}}\감마(2n+{5}{6}}) \감마(2n+{\frac {1}{1}{6})\왼쪽({\frac {3}{4}\오른쪽)^{2n}{2n}{2\pi(2n)!z^{3n}}\오른쪽]\ \[6pt]&{}-{\frac {\cos \left\frac {2}{3}z^{3}{3}}{2}}+{\frac {}{4}}\오른쪽) }}{{\sqrt{\pi}}\z^{1}{1}}}\왼쪽[\sum _{n=0}^{\inflt }{\dfrac {(-1)^{n}}\감마(2n+{\frac{11}{6}}}}}}}} \감마(2n+{\frac {7}{6})\왼쪽({\frac {3}{4}\오른쪽)^{2n+1}{2n+1}{2\pi(2n+1)! z^{3n+3/2}}\\오른쪽]\ \[6pt]\operatorname {Bi}(-z)\sim &}{{}{\frac {2}{3}}}z^{3}{3}}}{\frac {}}}{\frac {}}}{4}}\right) }}{{\sqrt{\pi}}\z^{1}{1}}}\왼쪽[\sum _{n=0}^{\inflt }{\dfrac {(-1)^{n}}\감마(2n+{5}{6}}) \감마(2n+{\frac {1}{1}{6})\왼쪽({\frac {3}{4}\오른쪽)^{2n}{2n}{2\pi(2n)!z^{3n}}\오른쪽]\ \[6pt]&{}+{\frac {\sin \left\frac {2}}{3}z^{3}{3}}{2}}+{\frac {}}{4}}\오른쪽) }}{{\sqrt{\pi}}\z^{1}{1}}}\왼쪽[\sum _{n=0}^{\inflt }{\dfrac {(-1)^{n}}\감마(2n+{\frac{11}{6}}}}}}}} \감마(2n+{\frac {7}{6})\왼쪽({\frac {3}{4}\오른쪽)^{2n+1}{2n+1}{2\pi(2n+1)! z^{3n+3/2}}:\오른쪽]. \end{정렬}}}
arg(z ) 0일 때, 이는 좋은 근사치지만, Ai(-z ) 또는 Bi(-z ) 와 위의 근사치 사이의 비율이 사인 또는 코사인(cosine)이 0이 될 때마다 무한대로 가기 때문에 무증상 근사치는 아니다.이러한 한계에 대한 점증적 팽창 도 이용할 수 있다. 이것들은 (Abramowitz and Stegun, 1983)와 (Olver, 1974년)에 열거되어 있다.
파생상품인 '아이'(z) 와 '비'(z )에 대해서도 점증적 표현을 얻을 수 있다. 이전과 마찬가지로, arg(z ) when [3]
아이 ′ ( z ) ∼ − z 1 4 e − 2 3 z 3 2 2 π [ ∑ n = 0 ∞ 1 + 6 n 1 − 6 n ( − 1 ) n Γ ( n + 5 6 ) Γ ( n + 1 6 ) ( 3 4 ) n 2 π n ! z 3 n / 2 ] . {\displaystyle \operatorname {Ai} '(z)\sim -{\dfrac {z^{\frac {1}{4}}e^{-{\frac {2}{3}}z^{\frac {3}{2}}}}{2{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {1+6n}{1-6n}}{\dfrac {(-1)^{n}\Gamma (n+{\frac {5}{6}}) \감마(n+{\frac {1}{6})\왼쪽({\frac {3}{4}}\오른쪽) ^{n}}{2\pi n!z^{3n/2}}\오른쪽]. }
arg(z ) π /3[3]
비 ′ ( z ) ∼ z 1 4 e 2 3 z 3 2 π [ ∑ n = 0 ∞ 1 + 6 n 1 − 6 n Γ ( n + 5 6 ) Γ ( n + 1 6 ) ( 3 4 ) n 2 π n ! z 3 n / 2 ] . {\displaystyle \operatorname {Bi} '(z)\sim {\frac {z^{\frac {1}{4}}e^{{\frac {2}{3}}z^{\frac {3}{2}}}}{{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {1+6n}{1-6n}}{\dfrac {\Gamma (n+{\frac {5}{6}}) \감마(n+{\frac {1}{6})\왼쪽({\frac {3}{4}}\오른쪽) ^{n}}{2\pi n!z^{3n/2}}\오른쪽]. }
마찬가지 arg () 2π/3 >일 때의 ai(-z ) 와 Bi'(-z ) 의 표현은 다음과[3]
아이 ′ ( − z ) ∼ − z 1 4 cas ( 2 3 z 3 2 + π 4 ) π [ ∑ n = 0 ∞ 1 + 12 n 1 − 12 n ( − 1 ) n Γ ( 2 n + 5 6 ) Γ ( 2 n + 1 6 ) ( 3 4 ) 2 n 2 π ( 2 n ) ! z 3 n ] − z 1 4 죄를 짓다 ( 2 3 z 3 2 + π 4 ) π [ ∑ n = 0 ∞ 7 + 12 n − 5 − 12 n ( − 1 ) n Γ ( 2 n + 11 6 ) Γ ( 2 n + 7 6 ) ( 3 4 ) 2 n + 1 2 π ( 2 n + 1 ) ! z 3 n + 3 / 2 ] 비 ′ ( − z ) ∼ z 1 4 죄를 짓다 ( 2 3 z 3 2 + π 4 ) π [ ∑ n = 0 ∞ 1 + 12 n 1 − 12 n ( − 1 ) n Γ ( 2 n + 5 6 ) Γ ( 2 n + 1 6 ) ( 3 4 ) 2 n 2 π ( 2 n ) ! z 3 n ] − z 1 4 cas ( 2 3 z 3 2 + π 4 ) π [ ∑ n = 0 ∞ 7 + 12 n − 5 − 12 n ( − 1 ) n Γ ( 2 n + 11 6 ) Γ ( 2 n + 7 6 ) ( 3 4 ) 2 n + 1 2 π ( 2 n + 1 ) ! z 3 n + 3 / 2 ] {\displaystyle{\begin}\operatorname {Ai} '(-z)\sim &}-{}-{\frac {z^{1}{4}}}}\cos \좌측({\frac {2}{3}}}}}}{2}}+{\frac {\pi}}}}}\오른쪽) }{{\sqrt {\pi }\}}\왼쪽[\sum _{n=0}^{\inflt }{1+12n}{1-12n}}{\dfrac {(-1)^{n}\감마(2n+{5}{6}}) \감마(2n+{\frac {1}{1}{6})\왼쪽({\frac {3}{4}\오른쪽)^{2n}{2n}{2\pi(2n)!z^{3n}}\오른쪽]\ \[6pt]&{}-{\frac {z^{1}{1}:{4}\sin \left\frac {2}{3}}}z^{3}}{3}}}}}{\frac {}}}{4}}\right) }{{\sqrt {\pi }\}}\왼쪽[\sum _{n=0}^{\inflt }{7+12n}{-5-12n}}{\dfrac {(-1)^{n}\감마(2n+{11}{6}}) \감마(2n+{\frac {7}{6})\왼쪽({\frac {3}{4}\오른쪽)^{2n+1}{2n+1}{2\pi(2n+1)! z^{3n+3/2}}\\오른쪽]\ \[6pt]\operatorname {Bi} '(-z)\sim &}{{}{\frac {1}{1}{1}}}\sin \좌({\frac {2}{3}z^{3}}}}}{3}}}}}}{4}}\우) }{{\sqrt {\pi }\}}\왼쪽[\sum _{n=0}^{\inflt }{1+12n}{1-12n}}{\dfrac {(-1)^{n}\감마(2n+{5}{6}}) \감마(2n+{\frac {1}{1}{6})\왼쪽({\frac {3}{4}\오른쪽)^{2n}{2n}{2\pi(2n)!z^{3n}}\오른쪽]\ \[6pt]&{}-{\frac {z^{\frac {1}{1}:{4}\cos \left\frac {2}{3}}z^{3}}{3}}}}{\frac {}}}{4}}\frac) }{{\sqrt {\pi }\}}\왼쪽[\sum _{n=0}^{\inflt }{7+12n}{-5-12n}}{\dfrac {(-1)^{n}\감마(2n+{11}{6}}) \감마(2n+{\frac {7}{6})\왼쪽({\frac {3}{4}\오른쪽)^{2n+1}{2n+1}{2\pi(2n+1)! z^{3n+3/2}}\\오른쪽]\ \end{정렬}}}
복잡한 인수 우리는 에어리 함수의 정의를 다음과 같이 복잡한 평면으로 확장할 수 있다.
아이 ( z ) = 1 2 π i ∫ C 생략하다 ( t 3 3 − z t ) d t , {\displaystyle \operatorname {Ai}={\frac {1}{2\pi i}\int_{C}\exp \left({\tfrac {t^{3}}}}}{3}}-zt\,}\,dt,} 여기서 적분은 무한대의 지점에서 시작하여 무한대의 지점에서 시작하며 -1998/3 인수로 끝나는 경로 C 위 에 있다. 또는 미분방정식 y ′′ xy 0 을 사용하여 복잡한 평면의 전체 함수 로 Ai(x ) 와 Bi(x ) 를 확장할 수 있다.
ai(x )에 대한 점증식 공식은 x 의2/3 주값을 취하여 x가 음의 실제 축으로부터 멀리 떨어져 있으면 복잡한 평면에서 여전히 유효하다. Bi(x )의 공식은 유효하다. x 는 일부 양의 Δ에 대해 {x ∈ C arg(x ) < ( (/3 ) - Δ} 섹터에 있다. 마지막으로 ai(-x )와 Bi(-x ) 의 공식은 x {x x arg(x ) <(2 (/3) - Δ} 섹터에 있으면 유효하다.
그것은 Ai(x )와 Bi(x ) 모두 음의 실제 축에 0의 무한성을 갖는 에어리 함수의 점증거동으로부터 나타난다. Ai(x )함수는 복합평면에 다른 0이 없는 반면, Bi (x)함수는 또한 {z :C 3/3 < arg ( π /2}
플롯 ℜ [ 아이 ( x + i y ) ] {\displaystyle \re \left[\operatorname {Ai}(x+iy)\right]} ℑ [ 아이 ( x + i y ) ] {\displaystyle \Im \left[\operatorname {Ai}(x+iy)\right]} 아이 ( x + i y ) {\displaystyle \operatorname {Ai}(x+iy) \,} 아그 [ 아이 ( x + i y ) ] {\displaystyle \operatorname {arg} \left[\operatorname {Ai}(x+iy)\right]\,}
ℜ [ 비 ( x + i y ) ] {\displaystyle \re \left[\operatorname {Bi}(x+iy)\right]} ℑ [ 비 ( x + i y ) ] {\displaystyle \Im \left[\operatorname {Bi}(x+iy)\right]} 비 ( x + i y ) {\displaystyle \operatorname {Bi}(x+iy) \,} 아그 [ 비 ( x + i y ) ] {\displaystyle \operatorname {arg} \left[\operatorname {Bi}(x+iy)\right]\,}
기타 특수 기능과의 관계 양의 인수의 경우 에어리 함수는 수정된 베셀 함수 와 관련이 있다.
아이 ( x ) = 1 π x 3 K 1 3 ( 2 3 x 3 2 ) , 비 ( x ) = x 3 ( I 1 3 ( 2 3 x 3 2 ) + I − 1 3 ( 2 3 x 3 2 ) ) . {\displaystyle {\begin{aligned}\operatorname {Ai} (x)&{}={\frac {1}{\pi }}{\sqrt {\frac {x}{3}}}\,K_{\frac {1}{3}}\left({\tfrac {2}{3}}x^{\frac {3}{2}}\right),\\\operatorname {Bi} (x)&{}={\sqrt {\frac {x}{3}}}\left(I_{\frac {1}{3}}\left({\tfrac {2}{3}}x^{\frac {3}{2}}\right)+ I_{-{\frac {1}{3}}\좌측({\tfrac {2}{3}x^{3}{3}{3}{2}}\우측)\우측)). \end{정렬}}} 여기 ±1/3 , 나와 1/3 x 2 y ″ + x y ′ − ( x 2 + 1 9 ) y = 0. {\displaystyle x^{2}y'+xy'-\왼쪽(x^{2}+{\tfrac {1}{9}\오른쪽)y=0. }
에어리 함수의 첫 번째 파생 모델은
A i ′ ( x ) = − x π 3 K 2 3 ( 2 3 x 3 2 ) . {\displaystyle \operatorname {Ai'}(x)=-{\frac {x}{\pi {\sqrt{3}}}\,K_{\frac {2}}{3}}\좌({\tfrac {2}}{3}{3}}2}}\우). }
함수 K 와1/3 K 는2/3 빠른 수렴 통합의[4] 수정된 Besel 함수 참조).
음수 인수의 경우 에어리 함수는 베셀 함수 와 관련이 있다.
아이 ( − x ) = x 9 ( J 1 3 ( 2 3 x 3 2 ) + J − 1 3 ( 2 3 x 3 2 ) ) , 비 ( − x ) = x 3 ( J − 1 3 ( 2 3 x 3 2 ) − J 1 3 ( 2 3 x 3 2 ) ) . {\displaystyle{\begin}\operatorname {Ai}(-x)&}={\sqrt {\\\frac{9}}}}\좌측(J_{\\prac {1}{1}{3}}}}{3}}}{3}\우측) J_{-{\frac {1}{3}}}\left({\tfrac {2}{3}}x^{\frac {3}{2}}\right)\right),\\\operatorname {Bi} (-x)&{}={\sqrt {\frac {x}{3}}}\left(J_{-{\frac {1}{3}}}\left({\tfrac {2}{3}}x^{\frac {3}{2}}\right)-J_{\frac {1}{3}}\left({\tfrac {2}{3}}x^{\frac {3}{2}}\right)\right). \end{정렬}}} 여기서 J 는±1/3 의 해결책이다. x 2 y ″ + x y ′ + ( x 2 − 1 9 ) y = 0. {\displaystyle x^{2}y'+xy'+\왼쪽(x^{2}-{\tfrac {1}{9}\오른쪽)y=0. }
득점자의 함수 Hi (x)와 -Gi (x)는 y ′′ - xy = 1/4을 해결한다.또한 에어리 함수의 측면에서도 다음과 같이 표현할 수 있다.
GI ( x ) = 비 ( x ) ∫ x ∞ 아이 ( t ) d t + 아이 ( x ) ∫ 0 x 비 ( t ) d t , 안녕 ( x ) = 비 ( x ) ∫ − ∞ x 아이 ( t ) d t − 아이 ( x ) ∫ − ∞ x 비 ( t ) d t . {\displaystyle{\begin{정렬}\operatorname{기}())&,{}=\operatorname{비},{}=\operatorname{비}_{-\infty}^{)}\operatorname{아이}(t)\,dt-\operatorname{아이}())\int _{-\infty}^{)}\operatorname())\int{B_{)}^{\infty}\operatorname{아이}(t)\,dt+\operatorname{아이}())\int _{0}^{)}\operatorname{비}(t)\,dt,\\\operatorname{안녕하세요}())&())\int나는}(t)\, dt.\end{aigned}}
푸리에 변환 에어리 함수 Ai(x )의 정의를 이용하면 푸리에 변환 이 주어지는 것을 쉽게 보여줄 수 있다.
F ( 아이 ) ( k ) := ∫ − ∞ ∞ 아이 ( x ) e − 2 π i k x d x = e i 3 ( 2 π k ) 3 . {\displaystyle {\mathcal {F}(\operatorname {Ai})(k): =\int _{-\pi k)^{{-\infit }^{\infit }\operatorname {Ai}\ e^{-2\pi ikx}\,dx=e^{\frac {i}{3}}}}{3}}}}. }
적용들 양자역학 에어리 함수는 삼각 전위 우물 안 에 갇힌 입자와 1차원 상수력장 입자에 대한 시간 독립 슈뢰딩거 방정식 의 해법이다. 같은 이유로, 위치의 선형 함수에 의해 전위가 국소적으로 근사할 수 있는 경우, 그것은 또한 WKB 근사치의 전환점 근처에 균일한 반전도 근사치를 제공하는 역할을 한다. 삼각형 전위 웰 용액은 반도체 이질 결합에 갇힌 전자의 이해와 직접적으로 관련이 있다.
광학 전기장 프로파일이 에어리 함수에 의해 주어지는 횡단 비대칭 광학 빔은 대칭 빔의 경우와 같이 직선으로 전파되는 대신 최대 강도의 흥미로운 특성이 한쪽으로 가속 된다. 이것은 저강도 꼬리가 반대 방향으로 펼쳐지는 것을 희생하는 것이므로, 빔의 전체적인 모멘텀은 당연히 보존되어 있다.
카우스틱스 에어리 기능은 무지개와 같은 광학 방향 가성체 근처의 강도의 형태에 기초한다. 역사적으로 이것은 에어리가 이 특별한 기능을 개발하도록 이끈 수학적인 문제였다.
역사 에어리 함수는 영국 의 천문학자 겸 물리학자 인 조지 비델 에어리 (1801–1892)의 이름을 따온 것으로, 물리학의 광학 초기 연구(에어리 1838)에서 이를 접했다. 아이(x )라는 표기법은 해롤드 제프리스 에 의해 도입되었다. 에어리는 1835년에 영국 천문학자 로얄 이 되었고 1881년에 은퇴할 때까지 그 자리를 지켰다.
참고 항목 메모들 ^ 데이비드 E. Aspense, Physical Review, 147 , 554 (1966) ^ a b 아브라모위츠 & 스테건(1983 , 페이지 448), Eqns 10.4.59, 10.4.61^ a b c d 아브라모위츠 & 스테건(1983년 , 페이지 448년), Eqns 10.4.60 및 10.4.64^ M. Kh. Khokonov. 하드 광자 // JETP, V.99, No.4, 페이지 690-707 \ (2004)의 방출에 의한 캐스케이드 에너지 손실 프로세스
참조 Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [June 1964]. "Chapter 10" . Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables ISBN 978-0-486-61272-0 LCCN 64-60036 . MR 0167642 . LCCN 65-12253 .Airy (1838), "On the intensity of light in the neighbourhood of a caustic" , Transactions of the Cambridge Philosophical Society , University Press, 6 : 379–402, Bibcode :1838TCaPS...6..379A 프랭크 윌리엄 존 올버 (1974년).점증약물과 특수함수, 11장.뉴욕, 아카데미 프레스. Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 6.6.3. Airy Functions" , Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8 Vallée, Olivier; Soares, Manuel (2004), Airy functions and applications to physics ISBN 978-1-86094-478-9 MR 2114198 , archived from the original on 2010-01-13, retrieved 2010-05-14 외부 링크 "Airy functions" , Encyclopedia of Mathematics EMS Press , 2001 [1994]Weisstein, Eric W. "Airy Functions" . MathWorld Ai 및 Bi 기능에 대한 Wolfram 함수 페이지.공식, 함수 평가자 및 플롯 계산기 포함. Olver, F. W. J. (2010), "Airy and related functions" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248

























![{\displaystyle \operatorname {Bi} (x)={\frac {1}{\pi }}\int _{0}^{\infty }\left[\exp \left(-{\tfrac {t^{3}}{3}}+xt\right)+\sin \left({\tfrac {t^{3}}{3}}+xt\right)\,\right]dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3bcd1d018bad9c90fe2a8575dbb9038f2371ad4)


![{\displaystyle \operatorname {Ai} (z)\sim {\dfrac {e^{-{\frac {2}{3}}z^{\frac {3}{2}}}}{2{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (n+{\frac {5}{6}})\Gamma (n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{n}}{2\pi n!z^{3n/2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ac0de3f47f959911543e5cbabb8098ae5bb3cc8)
![{\displaystyle \operatorname {Bi} (z)\sim {\frac {e^{{\frac {2}{3}}z^{\frac {3}{2}}}}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {\Gamma (n+{\frac {5}{6}})\Gamma (n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{n}}{2\pi n!z^{3n/2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c08bd4d24ec332406e1c1a96d83002b8e3be44ac)
![{\displaystyle {\begin{aligned}\operatorname {Ai} (-z)\sim &{}{\frac {\sin \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (2n+{\frac {5}{6}})\Gamma (2n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{2n}}{2\pi (2n)!z^{3n}}}\right]\\[6pt]&{}-{\frac {\cos \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (2n+{\frac {11}{6}})\Gamma (2n+{\frac {7}{6}})\left({\frac {3}{4}}\right)^{2n+1}}{2\pi (2n+1)!z^{3n+3/2}}}\right]\\[6pt]\operatorname {Bi} (-z)\sim &{}{\frac {\cos \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (2n+{\frac {5}{6}})\Gamma (2n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{2n}}{2\pi (2n)!z^{3n}}}\right]\\[6pt]&{}+{\frac {\sin \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\Gamma (2n+{\frac {11}{6}})\Gamma (2n+{\frac {7}{6}})\left({\frac {3}{4}}\right)^{2n+1}}{2\pi (2n+1)!z^{3n+3/2}}}\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88a8b6907a3908d270c8d98fa305880b40caee7b)
![{\displaystyle \operatorname {Ai} '(z)\sim -{\dfrac {z^{\frac {1}{4}}e^{-{\frac {2}{3}}z^{\frac {3}{2}}}}{2{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {1+6n}{1-6n}}{\dfrac {(-1)^{n}\Gamma (n+{\frac {5}{6}})\Gamma (n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{n}}{2\pi n!z^{3n/2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d491607498d24f9877d42607185e408a784e8e51)
![{\displaystyle \operatorname {Bi} '(z)\sim {\frac {z^{\frac {1}{4}}e^{{\frac {2}{3}}z^{\frac {3}{2}}}}{{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {1+6n}{1-6n}}{\dfrac {\Gamma (n+{\frac {5}{6}})\Gamma (n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{n}}{2\pi n!z^{3n/2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56643de7b1a34d11f96e74847567dfbe63f56c9f)
![{\displaystyle {\begin{aligned}\operatorname {Ai} '(-z)\sim &{}-{\frac {z^{\frac {1}{4}}\cos \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {1+12n}{1-12n}}{\dfrac {(-1)^{n}\Gamma (2n+{\frac {5}{6}})\Gamma (2n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{2n}}{2\pi (2n)!z^{3n}}}\right]\\[6pt]&{}-{\frac {z^{\frac {1}{4}}\sin \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {7+12n}{-5-12n}}{\dfrac {(-1)^{n}\Gamma (2n+{\frac {11}{6}})\Gamma (2n+{\frac {7}{6}})\left({\frac {3}{4}}\right)^{2n+1}}{2\pi (2n+1)!z^{3n+3/2}}}\right]\\[6pt]\operatorname {Bi} '(-z)\sim &{}{\frac {z^{\frac {1}{4}}\sin \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {1+12n}{1-12n}}{\dfrac {(-1)^{n}\Gamma (2n+{\frac {5}{6}})\Gamma (2n+{\frac {1}{6}})\left({\frac {3}{4}}\right)^{2n}}{2\pi (2n)!z^{3n}}}\right]\\[6pt]&{}-{\frac {z^{\frac {1}{4}}\cos \left({\frac {2}{3}}z^{\frac {3}{2}}+{\frac {\pi }{4}}\right)}{{\sqrt {\pi }}\,}}\left[\sum _{n=0}^{\infty }{\frac {7+12n}{-5-12n}}{\dfrac {(-1)^{n}\Gamma (2n+{\frac {11}{6}})\Gamma (2n+{\frac {7}{6}})\left({\frac {3}{4}}\right)^{2n+1}}{2\pi (2n+1)!z^{3n+3/2}}}\right]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9dbab547f916956f832ac4325e5ed3266c8f54bd)

![{\displaystyle \Re \left[\operatorname {Ai} (x+iy)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92d14f4ea89c98289bdd7724aa97a65bc37be26c)
![{\displaystyle \Im \left[\operatorname {Ai} (x+iy)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f188455d8f10f38330bed9927837e68fdbc9df46)

![{\displaystyle \operatorname {arg} \left[\operatorname {Ai} (x+iy)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2722a1be5b008fee5231676bfbecc9a6a15f6da)
![{\displaystyle \Re \left[\operatorname {Bi} (x+iy)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a2dd29c05abcff762111d663f165d7c1055d3de)
![{\displaystyle \Im \left[\operatorname {Bi} (x+iy)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/456ed57b8b06b7da31229c0cb6989b24c2d9b3d8)

![{\displaystyle \operatorname {arg} \left[\operatorname {Bi} (x+iy)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef422f3f85b66c485cf5b87ffa8b57b1b3e254a1)









