가성(광학)

물 한 잔에 의한 가성 물질

광학에서 가성 네트워크(austic^[1] network)는 곡면 또는 물체에 의해 반사 또는 굴절된 광선의 외피 또는 그 외피의 다른 ^[2]표면에 투영된 광선의 외피입니다.가성(austic)은 각 광선이 접하는 곡선 또는 표면으로, 광선의 외피 경계를 집중된 ^[2]광선의 곡선으로 정의합니다.따라서 오른쪽 사진에서는 가성 물질이 빛의 부분이나 밝은 가장자리로 보입니다.이러한 모양에는 종종 첨두 특이점이 있습니다.

찻잔 바닥에 있는 네프로이드 가성제

수면에 의한 가성 물질

얕은 물에서의 부식

설명.

평탄하지 않은 표면에 의해 굴절된 광선은 많은 광선이 교차하는 가성체를 형성한다.

빛의 집중, 특히 햇빛은 타오를 수 있다.가성이라는 단어는 사실 그리스어 αααααα υ , burnt , , , 、 the the 、 , , 、 , ca 、 ca ca 、 ca 、 ust ust 、 ca the 、

가성 물질이 보이는 일반적인 상황은 유리잔에 빛이 비치는 경우입니다.유리는 그림자를 드리우면서도 밝은 빛의 곡선 영역을 만들어냅니다.이상적인 상황(무한의 점원으로부터의 것처럼 완전히 평행한 광선을 포함한다)에서는 네프로이드 모양의 빛의 패치를 ^[3]^[4]생성할 수 있다.잔물결 모양의 가성 물질은 빛이 수역에서 파도를 통해 빛날 때 흔히 형성된다.

또 다른 친숙한 가성체는 ^[5]^[6]무지개이다.빗방울에 의한 빛의 산란은 다른 파장의 빛을 다른 반경의 호로 굴절시켜 활을 만든다.

컴퓨터 그래픽스

일반적인 와인 글라스 가성제 사진

와인잔 가성제 컴퓨터 렌더링

컴퓨터 그래픽스에서 대부분의 최신 렌더링 시스템은 가성비를 지원합니다.그 중 일부는 부피 측정 가성 물질까지 지원합니다.이는 광빔의 가능한 경로를 레이트레이스하여 굴절과 반사를 고려함으로써 달성됩니다.광자 매핑은 이것의 한 가지 구현입니다.체적 측정 가성은 체적 측정 경로 추적을 통해서도 달성할 수 있습니다.일부 컴퓨터 그래픽 시스템은 "전방 광선 추적"에 의해 작동하며, 광자는 광원에서 나와 규칙에 따라 주변 환경을 튕기는 것으로 모델링됩니다.충분한 광자가 표면에 부딪혀 장면의 평균 영역보다 밝아지는 영역에 가성체가 형성됩니다."백워드 광선 추적"은 표면에서 시작하여 ^[7]광원으로의 직접 경로가 있는지 여부를 판단하는 역방향으로 작동합니다.3D 광선 추적 가성체의 몇 가지 예는 여기에서 찾을 수 있습니다.

대부분의 컴퓨터 그래픽 시스템은 물리적 정확성보다는 미학에 중점을 두고 있습니다.물리적으로 정확한 계산 대신 일반적인 미리 계산된 텍스처가 주로 사용되는 컴퓨터 게임에서^[8] 실시간 그래픽의 경우 특히 그렇습니다.

가성 공학

가성 공학은 컴퓨터 그래픽스의 역문제를 해결하는 과정을 기술한다.즉, 특정 이미지가 주어지면 굴절 또는 반사된 빛이 이 이미지를 형성하는 표면을 결정합니다.

이 문제의 이산 버전에서 표면은 매끄러운 것으로 가정되는 여러 개의 마이크로 표면으로 분할된다. 즉, 각 마이크로 표면에 의해 반사/굴절된 빛이 가우스 가성체를 형성한다.가우스 가성(Gausian austic)은 각 마이크로 표면이 가우스 분포를 따르는 것을 의미합니다.그런 다음 포아송 통합과 시뮬레이션 ^[9]어닐링의 조합을 사용하여 각 마이크로 표면의 위치와 방향을 구한다.

지속적인 문제를 해결하기 위한 다양한 접근법이 있었다.하나의 접근법은 들어오는 광선과 목표 표면 사이의 매핑을 찾기 위해 최적^[10] 운송이라고 불리는 운송 이론의 아이디어를 사용합니다.이러한 매핑을 얻은 후 스넬의 ^[11]^[12]굴절 법칙을 이용하여 반복적으로 적응함으로써 표면을 최적화한다.

최적의 트랜스포트 기반 가성 패턴 설계

기본원칙

가성 패턴을 제어하는 것은 오히려 어려운 문제입니다. 왜냐하면 빛의 방향이 재료와 교차하여 굴절될 때 다른 광선의 간섭을 받을 수 있기 때문입니다.이로 인해 산란하고 불연속적인 패턴이 발생합니다.이 문제를 해결하기 위해 최적 트랜스포트 기반은 특정 투명 물질의 표면을 통과할 때 빛의 방향을 수정하여 가성 패턴을 제어하는 기존의 제안 방법 중 하나입니다.이는 최적의 전송에 기초한 ^[13]^[14]역최적화 문제를 해결함으로써 이루어집니다.물체/패턴의 기준 이미지가 주어지면, 그 목표는 빛이 굴절되어 기준 이미지의 유사한 패턴으로 수렴되는 재료 표면의 수학적 기술을 공식화하는 것이다.이것은 최적화 문제의 최소치에 도달할 때까지 초기 광도를 재배치/재호출함으로써 이루어집니다.

파이프라인 설계

여기서 굴절 가성 물질만을 고려하여 다음과 같이 목표를 결정할 수 있다(출력이 다른 반사 가성 물질에 대한 유사한 원리).

입력: 광원 위치에 따라 재료를 통해 빛을 전파한 후 얻을 수 있는 패턴 이미지.

출력: 리시버의 가성 형상(평탄한 고체 표면, 예를 들어 바닥, 벽 등)

목표 패턴을 달성하기 위해서는 빛이 굴절되어 외부 환경으로 나가는 표면을 재료의 다른 면에 원하는 패턴을 얻을 수 있도록 일정한 모양으로 제작해야 합니다.

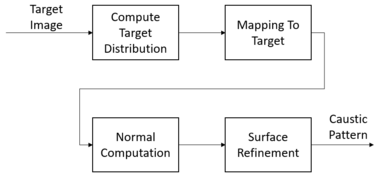
전술한 바와 같이 입력 이미지를 지정하면 이 프로세스는 출력과 동일한 가성 패턴을 생성합니다.원칙적으로 2개의 코어 스테이지가 있으며, 각 스테이지에는 2개의 서브 스테이지가 포함됩니다.

최적의 트랜스포트 기반 가성 설계
최적의 전송 문제 해결
1. 목표물 광분포 계산
2. 초기 배포에서 대상 배포로의 매핑 계산
대상 지표면 최적화
1. 표면의 정규 표현 계산
2. 표면 미세화

최적의 운송 문제 해결

투명한 표면을 통해 케이스 굴절이 발생하므로, 예를 들어 투명한 수면 아래에서 나타나는 패턴은 다음과 같은 3가지 주요 현상을 관찰할 수 있다.

매우 밝은(응축된 광도) 점(이른바 특이점)
점을 연결하는 곡선 모양의 객체
광도가 낮은 영역

계산을 수행하기 위해 패턴의 기하학적 특성을 설명하기 위해 점 특이점 $\Phi _{p}$ p \ $display$ style \ $Phi$ _ ${p}($ 특정 고농도 광점에서의 광강도 측정), 곡선 특이점 $\Phi _{c}$ c \ $display$ style \ $Phi$ _ ${c}($ 측정 길이)의 3가지 수량을 각각 도입하고 있다.t 광도) 및 방사선 강도 측정 $\Phi _{I}$ I( $표시$ 스타일 $\Phi$ _ ${I})($ 저농도 광도 영역에서의 강도 측정).이들을 종합하면 대상 표면의 특정 구간 δ에서 총 방사 플럭스 측정 $\Phi _{T}$ T \ $displaystyle \Phi$ _ ${T}$ 를 $\Phi _{T}$ 다음과 같이 정의한다.

\displaystyle \Phi _{T}(\Omega)=\textstyle \sum _{i=1}^{n_{i}(\delta}})\Phi _{p}^{i}(\sum _{j=1}^{N_{\gamma }}\Phi _{{{i}(\Omega})_{i}

이 단계 이후 $\Phi _{S}$ $\Phi _{S}$ \ $Phi _{S}($ 초기화에 의한 균일한 분포)와 대상 $\Phi _{T}$ T \ $Displaystyle \Phi$ _ ${T}($ 이전 단계에서 계산)의 방사 플럭스 측정에는 두 가지 기존 측정값이 있다.이제 소스에서 타깃으로의 매핑만 계산하면 됩니다.이를 위해 몇 가지 수량을 정의해야 합니다.우선 확률로 $\mu _{S}$ 한 2가지 광도: $μ$ $\mu _{S}$ S {\ $displaystyle \mu$ _{ $S}$ ( $\Phi _{S}$ $\Phi _{S}$ S $\Phi _{S}$ \ $displaystyle \Phi _{S$ })와 $\Phi _{S}$ $\Phi _{T}$ ${\display$ style \ $Phi$ _ ${S$ $}$ $}$ $\Phi _{T}$ μS μS ） $\mu _{T}$ ( $\Phi _{T}$ T $\Phi _{T}$ { $displaystyle$ \ $Phi$ _ { $T$ } $\Phi _{S}$ S { $\Phi _{S}$ \ $displaystyle$ \ $Phi$ _ { $S$ $\Phi _{S}$ } $\Phi _{T}$ T $\Phi _{T}$ \ $displaystyle$ \ $Phi _$ { T $\Phi _{T}$ } ） ( ( ( between between between between between between between between between between between between between between between between between between between between between between between between between between between between between between between between between between between between다음으로 소스 메쉬가 복수의 $s_{i}\in (\Phi _{S}\cup \Phi _{T})$ i $s_{i}\in (\Phi _{S}\cup \Phi _{T})$ $s_{i}\in (\Phi _{S}\cup \Phi _{T})$ $s_{i}\in (\Phi _{S}\cup \Phi _{T})$ {\ $s_{i}\in (\Phi _{S}\cup \Phi _{T})$ ） \ $displaystyle s$ _ { $i$ } \ $in$ ( \ $Phi$ _ { S $s_{i}\in (\Phi _{S}\cup \Phi _{T})$ } \ cup \ $Phi$ _ { $T$ } $s_{i}\in (\Phi _{S}\cup \Phi _{T})$ )로서 생성되어 나중에 변형됩니다.다음으로 중량 $\omega$ ${\$ { \ $displaystyle$ \ $omega$ $\omega$ 에 $s_{i}$ 의해 가중된 이 사이트의 $s_{i}$ { $s_{i}$ \ $displaystyle s$ { i $s_{i}$ } } this this this this this this this this this this this this this this $P_{w}$ $P_{w}$ P w \ $displaystyle P_{$ $w$ $}$ ( $C$ $C_{i}^{w}$ w { $displaystyle$ C _ { $i$ }^{ w $}$ 전원 셀 $C_{i}^{w}$ )를 정의합니다.마지막으로 이동해야 할 전원 셀을 결정합니다.표면의 $x개$ (\ $displaystyle$ x $)$ 정점을 $x$ 고려하여 다음 볼록함수의 $\omega _{min}$ $(\$ $\omega _{min}$ 를 찾으면 표적에 일치하는 전력도가 생성됩니다.

\displaystyle f(\obega)=\sum _{s_{i}\in S}(\obega _{i})\mu _{S}(C_{i}^{0})-\int \limits _{C_{i}^{\obega }}(x-s_{i}\^{2}-\obega _{i})d\mu _{T}(x)}})

대상 지표면 최적화

계산 프로세스

최적의 전송 문제를 해결한 후 정점이 달성됩니다.그러나 이것은 최종 표면이 어떻게 보여야 하는지에 대한 정보를 제공하지 않는다.입사 $d_{I}$ $($ 스타일 $d_{)$ 가 주어진 목표 표면을 달성하기 위해 $I$ 출력 $d_{O}$ $d_{O}$ O $(\$ 및 위의 $d_{O}$ 단계에서 얻은 전력 다이어그램은 표면 규범 표현을 Snell의 법칙에 따라 다음과 같이 계산할 수 있습니다.

\displaystyle n=d_{I}+{\eta x \over \lVert d_{I}+\eta d_{T}\rVert}=d_{I}+{\eta x \over \lVert d_{I}+\eta {(x_{R}-x)\over x_{R}-x}\rVert }}

어디에,

{\

{\displaystyle

\eta

\eta

} : 굴절계수

x_{R}

R

(\

상기의 최적의 수송 문제를 해결하여 얻은 목표 위치

정규 표현을 얻으면 다음과 같은 복합 에너지 함수를 최소화하여 표면 정교화를 달성할 수 있습니다.

{\operatorname {arg,max} }},\operatorname {arg,max} },\cdot [E_{int},E_{dir},E_{flux},E_{reg},E_{bar

어디에,

E_{int}=\sum _{v\in M_{T}}\lVert n_{o}-n\rVert _{2}^{2}

n

E_{int}=\sum _{v\in M_{T}}\lVert n_{o}-n\rVert _{2}^{2}

E_{int}=\sum _{v\in M_{T}}\lVert n_{o}-n\rVert _{2}^{2}

E_{int}=\sum _{v\in M_{T}}\lVert n_{o}-n\rVert _{2}^{2}

E_{int}=\sum _{v\in M_{T}}\lVert n_{o}-n\rVert _{2}^{2}

M

E_{int}=\sum _{v\in M_{T}}\lVert n_{o}-n\rVert _{2}^{2}

E_{int}=\sum _{v\in M_{T}}\lVert n_{o}-n\rVert _{2}^{2}

E_{int}=\sum _{v\in M_{T}}\lVert n_{o}-n\rVert _{2}^{2}

-

E_{int}=\sum _{v\in M_{T}}\lVert n_{o}-n\rVert _{2}^{2}

E_{int}=\sum _{v\in M_{T}}\lVert n_{o}-n\rVert _{2}^{2}

{

display

E

_ {int } =

\ sum _ { v \ in M _ {

T

} } \

lVert

n _ {

o

} - n \

rVert

_ { }

the

n

n_{o}

{\ no 、 {

display n

} obtained 2

obtained

2 obtained

n_{o}

2 。최적분에너지는 최적의 정점

n_{o}

。상기의 계산.

E

E_{dir}=\sum _{v\in M_{T}}\lVert x-{\textbf {proj}}_{(x_{S},\,d_{I})}(x)\rVert _{2}^{2}

r

E_{dir}=\sum _{v\in M_{T}}\lVert x-{\textbf {proj}}_{(x_{S},\,d_{I})}(x)\rVert _{2}^{2}

E_{dir}=\sum _{v\in M_{T}}\lVert x-{\textbf {proj}}_{(x_{S},\,d_{I})}(x)\rVert _{2}^{2}

E_{dir}=\sum _{v\in M_{T}}\lVert x-{\textbf {proj}}_{(x_{S},\,d_{I})}(x)\rVert _{2}^{2}

E_{dir}=\sum _{v\in M_{T}}\lVert x-{\textbf {proj}}_{(x_{S},\,d_{I})}(x)\rVert _{2}^{2}

T

E_{dir}=\sum _{v\in M_{T}}\lVert x-{\textbf {proj}}_{(x_{S},\,d_{I})}(x)\rVert _{2}^{2}

x -

E_{dir}=\sum _{v\in M_{T}}\lVert x-{\textbf {proj}}_{(x_{S},\,d_{I})}(x)\rVert _{2}^{2}

E_{dir}=\sum _{v\in M_{T}}\lVert x-{\textbf {proj}}_{(x_{S},\,d_{I})}(x)\rVert _{2}^{2}

E_{dir}=\sum _{v\in M_{T}}\lVert x-{\textbf {proj}}_{(x_{S},\,d_{I})}(x)\rVert _{2}^{2}

S ,

I

) (

E_{dir}=\sum _{v\in M_{T}}\lVert x-{\textbf {proj}}_{(x_{S},\,d_{I})}(x)\rVert _{2}^{2}

)

E_{dir}=\sum _{v\in M_{T}}\lVert x-{\textbf {proj}}_{(x_{S},\,d_{I})}(x)\rVert _{2}^{2}

2

E_{dir}=\sum _{v\in M_{T}}\lVert x-{\textbf {proj}}_{(x_{S},\,d_{I})}(x)\rVert _{2}^{2}

( \

displaystyle

E

_

{

dir

} =

E_{dir}=\sum _{v\in M_{T}}\lVert x-{\textbf {proj}}_{(x_{S},\,d_{I})}(x)\rVert _{2}^{2}

\

sum

_ { v \

in

M _ { T } \

lVert

x - { \ textbf {

proj }

} _ { { x _ { x _ { x _ { { { S ,

d

} } } } } } }

}

입사 광선에서 크게 변화하지 않도록 주의한다.

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

f

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

t

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

T

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

(

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

) -

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

S

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

( t

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

)

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

2

E_{flux}=\sum _{t\in M_{T}}\lVert \Phi _{T}(t)-\Phi _{S}(t_{s})\rVert _{2}^{2}

(

display

E

_

{

flux

} = \

sum

_ {

t

\

in

M _ {

T

} \

lVert

\

Phi

_ {

T

} ( t ) _ {

S

}

E_{reg}=\lVert {\textbf {L}}{\textbf {X}}\rVert _{2}^{2}

e

E_{reg}=\lVert {\textbf {L}}{\textbf {X}}\rVert _{2}^{2}

E_{reg}=\lVert {\textbf {L}}{\textbf {X}}\rVert _{2}^{2}

L

E_{reg}=\lVert {\textbf {L}}{\textbf {X}}\rVert _{2}^{2}

E_{reg}=\lVert {\textbf {L}}{\textbf {X}}\rVert _{2}^{2}

{

displaystyle

E _ {

reg

} = \

lVert

{

textbf {

L } } { \

rVert

_ {

2

}

e

to 、 삼각형의 형상을 정규화하는 에너지입니다.

E_{bar}=\sum _{v\in M_{T}}\lVert max(0,-log((1-n_{R}.(x-x_{R}))+d_{TH})\rVert ^{2}

TH

)\rVert ^{

2}}는

E_{bar}=\sum _{v\in M_{T}}\lVert max(0,-log((1-n_{R}.(x-x_{R}))+d_{TH})\rVert ^{2}

표면이 특정 거리

d_{TH}

d_{TH}

(\

d_

{)

를 초과하여 변형되지 않도록 하기 위한 장벽

에너지

입니다.

TH

차별화 가능한 역 렌더링 가성 패턴 설계

기본원칙

역그래픽은 이미지에서 데이터를 관찰하고 3D 지오메트리, 조명, 재료, 모션 등 가능한 모든 속성을 유추하여 사실적인 ^[15]이미지를 생성하는 방법입니다.기존의 컴퓨터 그래픽스에서는 원하는 모양과 효과를 가진 이미지를 렌더링하기 위해 모든 관련 특성/특성이 부여됩니다.이는 전송 방식이라고 할 수 있습니다.반대로, 가성 설계에서는 물체(특히 재료 표면)의 특성과 특성이 사소한 것이 아니다.지정된 구속조건은 취득할 대상 이미지입니다.따라서 대상 이미지를 관찰하고 유추하여 그 특성과 특성을 얻는 것이 목표입니다.이것은 역방향/역방향 방법으로 간주할 수 있습니다.

다음은 파라미터를 최적화하는 방법을 설명하는 기본적인 손실 함수입니다.

L(c)=\lVert f(c)-I\rVert ^{2}

어디에,

L (): c

손실 함수, 렌더링된 이미지의 평균 제곱 오차 및 대상

c

: 생성된 이미지에 영향을 줄 수 있는 요소가 포함되어 있습니다.

I

: 타깃 이미지

파이프라인 설계

차별화 가능한 역 렌더링 가성 설계

우선 타깃 패턴을 설계하고 포워드 패스를 계산하여 합성 패턴을 얻는다.목표 패턴과 비교해서 손해를 보는 거죠.반대는 합성 패턴이 대상 패턴과 최대한 유사하도록 하는 것입니다.그 후, 후방 전파를 실시해, 가성 제조에 필요한 최적화된 특성을 얻을 수 있습니다.

생성된 이미지에 기여하는 요소

외관( $A\displaystyle$ A $):$ 픽셀당 표면 외관은 맵된 텍스처와 픽셀당 밝기의 산물로 모델링됩니다.
지오메트리( $V$ {\ $displaystyle$ V $}):$ 3D 장면이 $정점$ V {\ $displaystyle$ V $V$ 로 파라미터화된 삼각형으로 근사된다고 가정합니다.
카메라( $\displaystyle$ C $):$ 초점거리, 시점, 카메라의 중심.

알베도나 굴절계수 등 더 많은 원소가 있을 수 있습니다.

일반적인 차별화 프레임워크

U를 2D 투영 정점 좌표 위치를 나타내는 중간 변수로 도입합니다.이러한 속성의 구배는 체인 규칙에 의해 간접적으로 도출될 수 있습니다.

{\displaystyle}{\frac V}=\frac U}배 {\frac U}{\partial V}}

(*displaystyle*********************************************************************************)

(\displaystyle\frac\fracC}=times\frac\frac\partialC})

확률적 경사 강하를 적용한 후 $A$ 의 A $(\displaystyle$ A $A$ $(\displaystyle$ V $)$ 및 $V$ $(\displaystyle$ C $)$ 를 $C$ 달성할 수 있었다.그 후, 이러한 수량은 목표 패턴을 생성하기 위해 재료를 조각하거나 밀링하는 데 사용됩니다.

실행

한 가지 일반적인 접근방식은 다음과 같은 다양한 딥 러닝 자동 차별화 프레임워크/라이브러리에서 차등 연산을 수행하는 능력을 활용하는 것입니다.텐서플로우, 파이토치, 테아노

또 하나의 접근방식은 OpenDR^[16] 프레임워크를 사용하여 전방 그래픽 모델을 구축하고 최적화를 위한 모델 파라미터에 대한 파생 모델을 자동으로 얻는 것입니다.최적화 특성을 얻을 수 있으므로 대상 화상을 생성할 수 있다.OpenDR은 확률론적 프로그래밍 프레임워크에 통합될 수 있는 국소 최적화 방법을 제공한다.이것은 가성 문제를 해결하기 위해 사용될 수 있다.

제조업

설계 및 제조 프로세스

가성 패턴이 계산적으로 설계되면 처리된 데이터는 제조 단계로 전송되어 최종 제품을 얻을 수 있습니다.가장 일반적인 방법은 감산 제조(기계)입니다.

원하는 품질, 제작 노력, 사용 가능한 제조 방법에 따라 다양한 재료를 사용할 수 있습니다.

일반 굴절 재료: 아크릴, 폴리카보네이트, 폴리에틸렌, 유리, 다이아몬드
일반반사재료:강,철,알루미늄,금,은,티타늄,니켈

아키텍처

가성 패턴 설계에는 다음과 같은 실제 응용 프로그램이 많이 있습니다.

조명기구
보석
아키텍처
장식 유리 제작

「」를 참조해 주세요.

레퍼런스

^ Lynch, DK; Livingston, W (2001). "The caustic network". Color and Light in Nature. Cambridge University Press. ISBN 978-0-521-77504-5.
^ ^a ^b Weinstein, Lev Albertovich (1969). Open Resonators and Open Waveguides. Boulder, Colorado: The Golem Press.
^ Circle Catacostic.울프램 매스월드2009-07-17 취득.
^ Levi, Mark (2018-04-02). "Focusing on Nephroids". SIAM News. Retrieved 2018-06-01.
^ 무지개 가성
^ 가성주름
^ Guardado, Juan (2004). "Chapter 2. Rendering Water Caustics". In Fernando, Randima (ed.). GPU Gems: Programming Techniques, Tips and Tricks for Real-Time Graphics. Addison-Wesley. ISBN 978-0321228321.
^ "Caustics water texturing using Unity 3D". Dual Heights Software. Retrieved May 28, 2017.
^ Marios Papas (April 2011). "Goal Based Caustics". Computer Graphics Forum (Proc. Eurographics). 30 (2).
^ Villani, Cedric (2009). Optimal Transport - Old and New. Springer-Verlag Berlin Heidelberg. ISBN 978-3-540-71049-3.
^ Philip Ball (February 2013). "Light tamers". New Scientist. 217 (2902): 40–43. Bibcode:2013NewSc.217...40B. doi:10.1016/S0262-4079(13)60310-3.
^ 안무 조명:새로운 알고리즘은 '원인'이라고 불리는 빛 패턴을 제어하여 일관된 이미지로 정리합니다.
^ Yuliy Schwartzburg, Romain Testuz, Andrea Tagliasacchi, Mark Pauly (2014). "High-contrast Computational Caustic Design" (PDF).{{cite web}}: CS1 maint: 여러 이름: 작성자 목록(링크)
^ Cédric, Villani (2009). Optimal Transport, Old and New. Springer. ISBN 978-3-540-71050-9.
^ Loper, Matthew M.; Black, Michael J. (2014), "OpenDR: An Approximate Differentiable Renderer", Computer Vision – ECCV 2014, Springer International Publishing, pp. 154–169, doi:10.1007/978-3-319-10584-0_11, ISBN 978-3-319-10583-3
^ Loper, Matthew M.; Black, Michael J. (2014), "OpenDR: An Approximate Differentiable Renderer", Computer Vision – ECCV 2014, Springer International Publishing, pp. 154–169, doi:10.1007/978-3-319-10584-0_11, ISBN 978-3-319-10583-3

Born, Max; Wolf, Emil (1999). Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (7th ed.). Cambridge University Press. ISBN 978-0-521-64222-4.
Nye, John (1999). Natural Focusing and Fine Structure of Light: Caustics and Wave Dislocations. CRC Press. ISBN 978-0-7503-0610-2.

추가 정보

Ferraro, Pietro (1996). "What a caustic!". The Physics Teacher. 34 (9): 572–573. Bibcode:1996PhTea..34..572F. doi:10.1119/1.2344572.
Dachsbacher, Carsten; Liktor, Gábor (February 2011). "Real-time volume caustics with adaptive beam tracing". Symposium on Interactive 3D Graphics and Games. ACM: 47–54.

[1] Lynch, DK; Livingston, W (2001). "The caustic network". Color and Light in Nature. Cambridge University Press. ISBN 978-0-521-77504-5.

[WEI69-2] Weinstein, Lev Albertovich (1969). Open Resonators and Open Waveguides. Boulder, Colorado: The Golem Press.

[3] Circle Catacostic.울프램 매스월드2009-07-17 취득.

[4] Levi, Mark (2018-04-02). "Focusing on Nephroids". SIAM News. Retrieved 2018-06-01.

[5] 무지개 가성

[6] 가성주름

[7] Guardado, Juan (2004). "Chapter 2. Rendering Water Caustics". In Fernando, Randima (ed.). GPU Gems: Programming Techniques, Tips and Tricks for Real-Time Graphics. Addison-Wesley. ISBN 978-0321228321.

[8] "Caustics water texturing using Unity 3D". Dual Heights Software. Retrieved May 28, 2017.

[9] Marios Papas (April 2011). "Goal Based Caustics". Computer Graphics Forum (Proc. Eurographics). 30 (2).

[10] Villani, Cedric (2009). Optimal Transport - Old and New. Springer-Verlag Berlin Heidelberg. ISBN 978-3-540-71049-3.

[11] Philip Ball (February 2013). "Light tamers". New Scientist. 217 (2902): 40–43. Bibcode:2013NewSc.217...40B. doi:10.1016/S0262-4079(13)60310-3.

[12] 안무 조명:새로운 알고리즘은 '원인'이라고 불리는 빛 패턴을 제어하여 일관된 이미지로 정리합니다.

[:0-13] Yuliy Schwartzburg, Romain Testuz, Andrea Tagliasacchi, Mark Pauly (2014). "High-contrast Computational Caustic Design" (PDF).{{cite web}}: CS1 maint: 여러 이름: 작성자 목록(링크)

[14] Cédric, Villani (2009). Optimal Transport, Old and New. Springer. ISBN 978-3-540-71050-9.

[15] Loper, Matthew M.; Black, Michael J. (2014), "OpenDR: An Approximate Differentiable Renderer", Computer Vision – ECCV 2014, Springer International Publishing, pp. 154–169, doi:10.1007/978-3-319-10584-0_11, ISBN 978-3-319-10583-3

[16] Loper, Matthew M.; Black, Michael J. (2014), "OpenDR: An Approximate Differentiable Renderer", Computer Vision – ECCV 2014, Springer International Publishing, pp. 154–169, doi:10.1007/978-3-319-10584-0_11, ISBN 978-3-319-10583-3

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

Search

가성(광학)

네임스페이스

더

목차

설명.

컴퓨터 그래픽스

가성 공학

최적의 트랜스포트 기반 가성 패턴 설계

기본원칙

파이프라인 설계

최적의 운송 문제 해결

대상 지표면 최적화

차별화 가능한 역 렌더링 가성 패턴 설계

기본원칙

파이프라인 설계

생성된 이미지에 기여하는 요소

일반적인 차별화 프레임워크

실행

제조업

「」를 참조해 주세요.

레퍼런스

추가 정보

Search

가성(광학)

설명.

컴퓨터 그래픽스

가성 공학

최적의 트랜스포트 기반 가성 패턴 설계

기본원칙

파이프라인 설계

최적의 운송 문제 해결

대상 지표면 최적화

차별화 가능한 역 렌더링 가성 패턴 설계

기본원칙

파이프라인 설계

생성된 이미지에 기여하는 요소

일반적인 차별화 프레임워크

실행

제조업

「 」를 참조해 주세요.

레퍼런스

추가 정보

「」를 참조해 주세요.