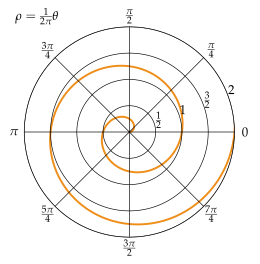
아르키메데스 나선

아르키메데스 나선형의 한 팔의 360° 루프 3개

아르키메데스 나선형(산술 나선형으로도 알려져 있음)은 기원전 3세기 그리스의 수학자 아르키메데스의 이름을 딴 나선형이다.일정한 각속도로 회전하는 선을 따라 일정한 속도로 고정된 지점에서 멀어지는 시간의 경과에 따른 위치에 대응하는 궤적입니다.마찬가지로 극좌표 $(r, θ$ )에서는 다음과 같이 나타낼 수 있다.

r=a+b\cdot\theta

실수

a

와 b를 붙입니다.

매개

변수 a를 변경하면 완화곡선의 중심점이 원점에서 바깥쪽으로(

양수

a는

θ

=

0

으로,

음수

a

는 θ =

θ

= θ 방향으로) 이동하며,

b

는 루프 사이의 거리를 제어합니다.

위의 방정식에서 출발점으로부터의 입자의 위치는 시간이 경과함에 따라 $각도θ$ 에 비례한다는 것을 알 수 있다.

아르키메데스는 그의 책 "나선형들"에서 그런 소용돌이를 묘사했다.사모스의 코논은 그의 친구였고 파푸스는 이 소용돌이가 코논에 ^[1]의해 발견되었다고 말한다.

나선형 일반방정식의 도출

아르키메데스 나선형의 개념을 이해하기 위해 아래에 물리적 접근법을 사용한다.

점 물체가 xy 평면에 대해 x축과 평행하게 향하는 $등속$ v로 데카르트 시스템에서 이동한다고 가정합니다. $시간$ t = $0일$ 때 개체는 임의 지점 $(c, 0, 0)$ 에 있었습니다. $xy$ 평면이 z축을 중심으로 일정한 각속도 $θ$ 로 회전하는 경우 z축에 대한 점의 속도는 다음과 같이 기록될 수 있다.

xy 평면은

시간

t의 원점에 대한 각도

δt

(안티클럭 방향)로 회전합니다. (

c, 0)

는

t

=

0

에서 물체의

위치

이며, P는 R

= vt

+

c

거리

에서 물체의 위치입니다.

{\displaystyle} v_{0} &=syslogrt {v^{2} +\Omega ^{2}(syslog+c)^{2}}\\v_{x}&=v\cos \omega t-\obega (c)\sin \mega t\v_{y}&=v\sin \omega t+\obega (c)\cos \omega t\end {aligned}

$여기$ 서 vt $+ c$ 는 임의의 $시점$ t에서의 입자의 위치 벡터의 $계수$ 이며_x, v는 x축을 따르는 속도 $성분$ 이며_y, v는 y축을 따르는 성분이다.아래 그림은 이를 설명하고 있습니다.

{\displaystyle\int v_{x},dt&=x\int v_{y},dt&=y\end {aligned}}

위의 방정식은 부품별 적분을 적용하여 다음과 같은 파라메트릭 방정식으로 통합될 수 있습니다.

(\displaystyle \displaystyle { aligned }x&=(cos + c)\cos \mega t\\y&=(cos + c)\sin \mega t\end {aligned}})

두 방정식을 제곱한 다음 (그리고 약간의 변경사항)을 더하면 데카르트 방정식이 된다.

{x^{2}+y^{2}}}}=harcfrac {v}{\obega}}}\cdot \arctan {y}{x}+c

자세한 내용은 사실ωt)θ과 θ)arctan.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output .sfr을 사용하여.Ac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}y/x)또는.

\displaystyle \tan \left(\displaystyle \t {x^{2}+y^{2}})-c\right)\cdot(\frac {flac }{v}}\right)=cdfrac {y}{x}}}}

그것의 극의 형태는

r=sysfrac {v}{\obega}}}\cdot \theta +c

호 길이 및 곡률

아르키메데스 나선형의 원접합으로 나선형에 접하며 접선점에 동일한 곡률을 가진다.나선 자체는 그려지지 않지만 원이 특히 서로 가까운 점으로 볼 수 있습니다.

데카르트 좌표의 매개 변수가 주어지면

(\displaystyle f\theta \mapsto (r,\cos \theta,r,\sin \theta )=(b,\theta,b,\cos \theta,\sin \theta)}

§

({

_

{1

~ §

({

_

{2})

의

\theta _{2}

호 길이는 다음과 같습니다.

{\frac {b} {\theta ^{2}} + \ln \left(\theta + {\theta {1+\theta ^{2}}\right)_{{1}}^{\theta_{2}

또는 동등하게:

{\frac {b} {\theta {1+\theta ^{2}} +\operatorname {arsinh} \theta \right]_{{1}}^{{2}}입니다.

따라서

\theta _{1}=0

1

\theta _{1}=0

\theta _{1}=0

（ \

displaystyle \theta

_ {1}

=

0 ）

\theta _{2}=\theta

2

\theta _{2}=\theta

（ \

displaystyle \theta

_ {2} = \

theta

}까지의

\theta _{2}=\theta

총 길이는 다음과 같습니다.

{\frac {b} {\theta ^{2}} + \ln \left(\theta + {\theta {1+\theta ^{2}}\right)\left [\theta }\theta ]

곡률은 다음과 같습니다.

\kappa = frac {\theta ^{2}+2}{b(\theta ^{2}+1)^{\frac {3}{2}}

특성.

극 그래프에 나타나는 아르키메데스 나선형

아르키메데스 나선은 원점에서 나오는 어떤 광선이 일정한 거리( $θ$ 가 라디안 단위로 측정되면 $2µb$ 와 동일)에서 나선의 연속적인 회전을 교차하는 특성을 가지고 있기 때문에 "산술 나선형"이라는 이름이 붙었다.이와는 대조적으로, 로그 나선형의 경우 원점에서 측정된 교차점의 거리뿐만 아니라 이러한 거리도 기하 급수를 형성합니다.

아르키메데스의 나선형은 두 개의 팔을 가지고 $있는데$ 하나는 $θ$ > 0이고 다른 $하나$ 는 $θ$ < 0이다.두 팔은 원점에서 부드럽게 연결되어 있습니다.함께 제공되는 그래프에는 암이 하나만 표시됩니다.Y축을 가로질러 이 암의 미러 이미지를 찍으면 다른 암이 생성됩니다.

$θ$ 가 클 경우, 점은 아르키메데스 나선을 따라 잘 근사한 균일한 가속도로 이동하는 반면, 나선은 일정한 각도로^[2] 회전하는 선을 따라 일정한 속도로 고정된 지점에서 멀어지는 시간에 따른 위치에 대응한다(Mikhail Gaichenkov의 기여 참조).

아르키메데스의 나선형이 커짐에 따라, 그 나선형은 점근적으로 $반지름$ v $/ θ$ 를 가진 원에 접근한다.

아르키메데스의 나선형

때때로 아르키메데스 나선이라는 용어는 보다 일반적인 나선 그룹에 사용된다.

r=a+b\cdot \theta ^{\frac {1}{c}}.

정상적인 아르키메데스 나선은 c = $1일$ 때 $발생$ 한다.이 그룹에 속하는 다른 나선형으로는 쌍곡선 나선형( $c$ = $-1$ ), 페르마의 나선형( $c$ = $2$ ) 및 리튜우스( $c$ = $-2$ )가 있다.

적용들

아르키메데스로 인해 원을 제곱하는 방법 중 하나는 아르키메데스의 나선형을 이용한다.아르키메데스는 또한 나선형이 어떻게 각도를 삼등분하는데 사용될 수 있는지를 보여주었다.두 방법 모두 고대 그리스 기하학적 ^[3]증거에서 직선과 나침반의 사용에 대한 전통적인 제한을 완화합니다.

스크롤 압축기의 메커니즘

아르키메데스의 나선형은 다양한 실제 응용 분야를 가지고 있다.가스를 압축하는 데 사용되는 스크롤 압축기는 두 개의 인터리브된 아르키메데스 나선,^[4] 아르키메데스 나선과 거의 비슷한 크기의 원의 인볼류트 또는 하이브리드 곡선으로 만들어질 수 있는 로터를 가지고 있습니다.

아르키메데스의 나선형은 나선형 안테나에서 찾을 수 있으며, 이것은 광범위한 주파수에 걸쳐 작동할 수 있다.

시계 밸런스 스프링의 코일과 초기 축음기 레코드의 홈은 아르키메데스의 나선형을 형성하여 균일한 간격으로 홈을 만들었다.^[5]

환자에게 아르키메데스의 나선형을 그려달라고 요청하는 것은 인간의 떨림을 수량화하는 방법이다; 이 정보는 신경학적 질병을 진단하는 데 도움이 된다.

아르키메데스 나선형은 디지털 빛 처리(DLP) 투영 시스템에서도 사용되어 "무지개 효과"를 최소화하며, 실제로는 빨간색, 녹색, 파란색이 매우 ^[6]빠르게 순환될 때 여러 색상이 동시에 표시되는 것처럼 보입니다.또한 아르키메데스 나선형은 나선형 ^[7]플래터를 통해 세균 농도를 정량화하기 위해 식품 미생물학에서 사용된다.

LL Pegasi의 Atacama Large Millimeter 배열 이미지

또한 실린더를 ^[8]^[9]감싼 일정한 두께의 종이 롤이나 테이프에서 발생하는 패턴을 모델링하는 데에도 사용됩니다.

많은 동적 나선형들(태양풍의 파커 나선형, 또는 캐서린 바퀴에 의해 만들어진 패턴)은 아르키메데스식이다.예를 들어, LL 페가수리는 자신을 둘러싼 먼지 구름에 있는 아르키메데스 나선형의 근사한 모습을 보여주며, 이중성계의 ^[10]일부로 다른 동반성에 의해 나선형으로 유도된 별에서 방출된 물질로 생각됩니다.

「」를 참조해 주세요.

레퍼런스

^ Ivor Bulmer-Thomas, "사모스의 코너", 과학 전기 3장 391절.
^ Sloane, N. J. A. (ed.). "Sequence A091154". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Boyer, Carl B. (1968). A History of Mathematics. Princeton, New Jersey: Princeton University Press. pp. 140–142. ISBN 0-691-02391-3.
^ Sakata, Hirotsugu; Masayuki Okuda. "Fluid compressing device having coaxial spiral members". Retrieved 2006-11-25.
^ Variable Groove의 내용을 참조하십시오Penndorf, Ron. "Early Development of the LP". Archived from the original on 5 November 2005. Retrieved 2005-11-25..
^ Ballou, Glen (2008), Handbook for Sound Engineers, CRC Press, p. 1586, ISBN 9780240809694
^ J. E. Gilchrist; J. E. Campbell; C. B. Donnelly; J. T. Peeler; J. M. Delaney (1973). "Spiral Plate Method for Bacterial Determination". Applied Microbiology. 25 (2): 244–52. doi:10.1128/AEM.25.2.244-252.1973. PMC 380780. PMID 4632851.
^ Tony Peressini (3 February 2009). "Joan's Paper Roll Problem" (PDF). Archived from the original (PDF) on 3 November 2013. Retrieved 2014-10-06.
^ Walser, H.; Hilton, P.; Pedersen, J.; Mathematical Association of America (2000). Symmetry. Mathematical Association of America. p. 27. ISBN 9780883855324. Retrieved 2014-10-06.
^ Kim, Hyosun; Trejo, Alfonso; Liu, Sheng-Yuan; Sahai, Raghvendra; Taam, Ronald E.; Morris, Mark R.; Hirano, Naomi; Hsieh, I-Ta (March 2017). "The large-scale nebular pattern of a superwind binary in an eccentric orbit". Nature Astronomy. Springer Science and Business Media {LLC}. 1 (3). doi:10.1038/s41550-017-0060.

외부 링크

[1] Ivor Bulmer-Thomas, "사모스의 코너", 과학 전기 3장 391절.

[2] Sloane, N. J. A. (ed.). "Sequence A091154". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.

[boyer-3] Boyer, Carl B. (1968). A History of Mathematics. Princeton, New Jersey: Princeton University Press. pp. 140–142. ISBN 0-691-02391-3.

[4] Sakata, Hirotsugu; Masayuki Okuda. "Fluid compressing device having coaxial spiral members". Retrieved 2006-11-25.

[5] Variable Groove의 내용을 참조하십시오Penndorf, Ron. "Early Development of the LP". Archived from the original on 5 November 2005. Retrieved 2005-11-25..

[6] Ballou, Glen (2008), Handbook for Sound Engineers, CRC Press, p. 1586, ISBN 9780240809694

[7] J. E. Gilchrist; J. E. Campbell; C. B. Donnelly; J. T. Peeler; J. M. Delaney (1973). "Spiral Plate Method for Bacterial Determination". Applied Microbiology. 25 (2): 244–52. doi:10.1128/AEM.25.2.244-252.1973. PMC 380780. PMID 4632851.

[uiuc-8] Tony Peressini (3 February 2009). "Joan's Paper Roll Problem" (PDF). Archived from the original (PDF) on 3 November 2013. Retrieved 2014-10-06.

[google-9] Walser, H.; Hilton, P.; Pedersen, J.; Mathematical Association of America (2000). Symmetry. Mathematical Association of America. p. 27. ISBN 9780883855324. Retrieved 2014-10-06.

[10] Kim, Hyosun; Trejo, Alfonso; Liu, Sheng-Yuan; Sahai, Raghvendra; Taam, Ronald E.; Morris, Mark R.; Hirano, Naomi; Hsieh, I-Ta (March 2017). "The large-scale nebular pattern of a superwind binary in an eccentric orbit". Nature Astronomy. Springer Science and Business Media {LLC}. 1 (3). doi:10.1038/s41550-017-0060.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Search

아르키메데스 나선

네임스페이스

더

목차

나선형 일반방정식의 도출

호 길이 및 곡률

특성.

아르키메데스의 나선형

적용들

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

아르키메데스 나선

나선형 일반방정식의 도출

호 길이 및 곡률

특성.

아르키메데스의 나선형

적용들

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.