오일러 나선

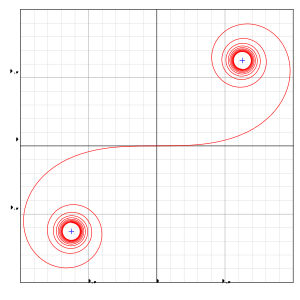
오일러 나선형은 곡선 길이에 따라 곡률이 선형으로 변하는 곡선입니다(원형 곡선의 곡률은 반지름의 역수와 같습니다). 곡선은 클로토이드 또는 코르누 나선이라고도 합니다.^[1]^[2] 프레넬 적분의 거동은 알프레드 마리 코르누 1874에 의해 최초로 만들어진 연결인 오일러 나선에 의해 설명될 수 있습니다.^[3] 오일러의 나선은 단조 곡률 함수의 성질을 갖는 초나선의 한 종류입니다.

오일러 나선은 회절 계산에 적용됩니다. 또한 철도 및 고속도로 공학에서 철도 또는 도로의 직선 및 곡선 구간 사이의 전환 곡선을 설계하는 데 널리 사용됩니다. 포토닉 집적 회로에서도 유사한 응용이 발견됩니다. 접선과 원형 곡선 사이의 전이 곡선 곡률의 선형 변화 원리는 오일러 나선의 기하학을 정의합니다.

곡선의 곡률은 직선 구간(접선)에서 0으로 시작하여 곡선 길이에 따라 선형적으로 증가합니다.
오일러 나선이 원곡선과 만나는 곳에서 곡선의 곡률은 후자의 곡률과 같아집니다.

역사

나선형에는 여러 필드에서 발견 및 응용 프로그램을 반영하는 여러 이름이 있습니다. 3대 분야는 탄성 스프링("Euler spiral", 1744), 빛 회절의 그래픽 계산("Cornu spiral", 1874), 철도 전환("철도 전환 나선", 1890)이었습니다.^[2]

레온하르트 오일러의 나선에 대한 연구는 제임스 베르누이가 탄성 이론에 문제를 제기한 후에 이루어졌습니다: 자유단을 눌러 평평하게 하면 직선이 될 정도로 미리 휘어진 와이어 스프링은 어떤 모양이어야 할까요? 오일러는 1744년에 나선형의 성질을 확립했고, 그 당시 곡선은 두 개의 극한을 가져야 한다고 언급했습니다, 즉 곡선이 빙글빙글 돌지만 결코 도달하지 않는 점들입니다. 38년 후인 1781년, 그는 ("행복한 우연"^[2]에 의해) 극한의 공식을 발견했다고 보고했습니다.

1818년 빛의 회절을 연구한 오거스틴 프레넬은 같은 나선을 정의하는 프레넬 적분을 개발했습니다. 그는 오일러의 적분이나 탄성 이론과의 연관성을 알지 못했습니다. 1874년 알프레드 마리 코르누는 그래프 위의 두 점 사이의 거리를 제곱함으로써 나선형의 그래프에서 회절 강도를 읽을 수 있다는 것을 보여주었습니다. 앙리 푸앵카레(Henri Poincare)는 코르누에 대한 전기적 스케치에서 "코누의 나선형"이 "털이 많은 불쾌한 통합 공식"에 비해 갖는 이점을 칭찬했습니다. 에르네스토 체사로(Ernesto Cesaro)는 그리스 신화에서 생명의 실타래를 돌리는 세 명의 운명 중 하나인 클로토(Clotho)의 이름을 따서 같은 곡선을 "클로토이드(clothoid)"라고 명명하기로 선택했습니다.^[2]

세 번째 독립적인 발견은 1800년대에 다양한 철도 기술자들이 선로 형태의 점진적인 곡률에 대한 공식을 추구했을 때 일어났습니다. 1880년 아서 뉴웰 탈보트는 적분 공식과 그 해를 계산했고, 그는 이것을 "철도 전환 나선형"이라고 불렀습니다. 오일러의 작품과의 연관성은 1922년에 이르러서야 이루어졌습니다.^[2]

적용들

추적 전이곡선

끝에 있는 것과 같은 곡률 반경을 가진 접선 원(오큘레이팅 원)을 가진 코르누 나선의 진화를 묘사한 애니메이션.

원형 경로를 따라 이동하기 위해서는 물체에 구심 가속도가 붙어야 합니다(예: 달은 중력 때문에 지구 주위를 돌고, 자동차는 구심력을 발생시키기 위해 앞바퀴를 안쪽으로 돌립니다). 직선 경로를 주행하는 차량이 갑자기 접선 원형 경로로 전환하는 경우, 접선 지점에서 0에서 필요한 값으로 갑자기 전환하는 구심 가속이 필요합니다. 이는 달성하기 어려울 것입니다(운전자가 스티어링 휠을 직선에서 회전 위치로 즉시 이동하는 경우를 생각해 보십시오, 그리고 자동차가 실제로 그러한 작업을 수행하고 있는 경우, 차량의 부품에 기계적 스트레스를 가하고 (측면 저크로 인해) 많은 불편을 초래합니다.

초기 철도에서는 저속과 넓은 반경의 곡선이 사용되었기 때문에 이러한 즉각적인 횡력의 적용은 문제가 되지 않았습니다(승객에 대한 횡력과 횡력은 작고 견딜 수 있었습니다). 수년간 철도 차량의 속도가 증가함에 따라 이동 거리에 따라 구심 가속도가 원활하게 증가하도록 완화가 필요하다는 것이 명백해졌습니다. 구심 가속도 v $/ r$ 의² 표현을 고려할 때, 명백한 해결책은 곡률 1 $/ R$ 이 이동 거리에 따라 선형적으로 증가하는 완화 곡선을 제공하는 것입니다. 이 기하학은 오일러 나선형의 다른 이름인 "클로로이드"입니다.^[5]

랭킨은 레온하르트 오일러에 의한 기하학의 해법을 알지 못한 채, 포물선이 원곡선에 대한 근사치인 것과 같은 방식으로 작은 각도 변화에 대한 오일러 나선의 근사치인 3차 곡선을 인용했습니다.

Marie Alfred Cornu (그리고 나중에 일부 토목 공학자들도)는 오일러 나선의 미적분학을 독립적으로 풀었습니다. 오일러 나선은 접선과 수평 원곡선 사이의 전이 또는 완화를 제공하기 위해 철도 및 고속도로 공학에서 널리 사용됩니다.

광학

광학에서는 "코누 나선형"이라는 용어가 사용됩니다.^[6]^{: 432} 코르누 나선은 회절 패턴을 설명하는 데 사용할 수 있습니다.^[7] $위상$ 진폭 $Ee$ 가 있는 평면파는 z = 0 $평면$ 에서 x = 0 위의 높이 h의 "knife 가장자리"에 의해 회절된다고 생각합니다. 그렇다면 회절파장은 다음과 같이 표현할 수 있습니다.

\mathbf {E} (x,z)=E_{0}e^{-jkz}{\frac {\mathrm {Fr}(\infty)-\mathrm {Fr} \left({\sqrt {\frac {2}{\lambda z}}(h-x)\right}{\mathrm {Fr}(\infty)-\mathrm {Fr}(-\infty)}

여기서

Fr(x)

는 복소평면에서 코르누 나선을 형성하는 프레넬 적분 함수입니다.

따라서 칼끝에서 회절될 때 평면파 감쇠 계산을 단순화하기 위해 적절한 $a$ 와 $b$ 에 대해 $Fr(a)$ 와 $Fr(b)$ 로 표시되는 점 사이의 물리적 거리로 양 $Fr(a)$ - $Fr(b)$ 를 표현하여 코르누 나선의 다이어그램을 사용할 수 있습니다. 이를 통해 칼끝 너머 위치 $(x,$ z $)$ 에서 $높이$ 의 칼끝에 의한 평면파의 감쇠를 대략적으로 계산할 수 있습니다.

통합광학

오일러 나선형을 따르는 곡률 반경이 연속적으로 변화하는 굽힘은 광 집적 회로의 손실을 줄이기 위해 단일 모드 도파관 또는 ^[8]^[9]방사 모드로의 급격한 곡률 변화를 매끄럽게 하고 결합을 억제하기 위해 또는 다중 모드 도파관에서 사용됩니다.^[10] 고차 모드로의 커플링을 억제하고 효과적인 단일 모드 작동을 보장하기 위해. 도파관에 오일러 나선의 선구적이고 매우 우아한 적용은 1957년에 마이크로파용 중공 ^[11]금속 도파관으로 이루어졌습니다. 여기서 아이디어는 직선 금속 도파관이 물리적으로 구부러져 오일러 나선과 같은 점진적인 굽힘 형태를 자연스럽게 취할 수 있다는 사실을 이용하는 것이었습니다.

파인만 경로 적분

양자역학의 경로 적분 공식에서 두 점 사이의 시간 단계별 작용 위상 화살표를 연결하여 두 점 사이의 전파에 대한 확률 진폭을 시각화할 수 있습니다. 화살표는 각 끝점을 중심으로 나선형으로 코르누 나선형이라고 하는 것을 형성합니다.^[12]

자동차 경주

모터스포츠의 저자인 Adam Brouillard는 턴의 코너 진입 부분에서 주행 라인을 최적화하는 오일러 스파이럴의 사용을 보여주었습니다.^[13]

타이포그래피 및 디지털 벡터 도면

Raph Levien은 2007년에^[14]^[15] 무료 라이선스로 Spiro를 곡선 디자인, 특히 글꼴 디자인을 위한 툴킷으로 출시했습니다. 이 툴킷은 폰트 디자인 툴 Fontforge와 디지털 벡터 드로잉 잉크스케이프에서 매우 빠르게 구현되었습니다.

지도투영

너비가 $1 / N$ 인 나선을 따라 구를 자르고 결과 모양을 평평하게 만들면 $n$ 이 무한대로 향할 때 오일러 나선이 생성됩니다.^[16] 구면이 지구인 경우 $n$ 이 무한대로 갈수록 왜곡이 0이 되는 지도 투영을 생성합니다.^[17]

거품기 모양

쥐 수염의 자연스러운 모양은 오일러 나선의 세그먼트로 잘 근사화됩니다. 단일 쥐의 경우 모든 수염은 동일한 나선의 세그먼트로 근사화될 수 있습니다.^[18] 오일러 나선 세그먼트에 대한 체사로 방정식의 두 매개변수는 거품기 성장의 각질화 메커니즘에 대한 통찰력을 제공할 수 있습니다.^[19]

공식화

기호

$R$	곡률반경
$R c$	나선 끝의 원곡선 반지름
$θ$	나선의 시작(무한 $R$ )에서 나선의 특정 지점까지의 곡선 각도입니다. 이는 초기 접선과 해당 지점의 접선 사이의 각도로도 측정할 수 있습니다.
$θ s$	전체 나선형 곡선의 각도
$L$ , $s$	초기 위치에서 나선형 곡선을 따라 측정한 길이
$L s$ , $s o$	나선곡선의 길이

파생

오른쪽 그래프는 주어진 두 곡선(이 경우 직선( $음$ 의 x축)과 원) 사이의 완화(전이) 곡선으로 사용되는 오일러 나선을 보여줍니다. 나선은 양의 $x$ 방향 원점에서 시작하여 점차 시계 반대 방향으로 돌면서 원을 진동시킵니다.

나선은 1사분면에 있는 위의 더블 엔드 오일러 나선의 작은 부분입니다.

만곡의 정의에서 볼 때,

{\frac {1}{R}}={\frac {d\theta }{ds}}\propto s

예.,

{begin{aligned}Rs={\text{constant}}&=R_{c}s_{o}\{\frac{d\theta}{ds}}&={\frac{s}{R_{c}s_{o}}\end{aligned}

우리는 형식으로 적습니다.

{\frac {d\theta }{ds}}=2a^{2}s

어디에

2a^{2}={\frac {1}{R_{c}s_{o}}}

아니면

a={\frac {1}{\sqrt {2R_{c}s_{o}}}}

따라서

\theta = (as)^{2}

지금이다

x=\int_{0}^{L}\cos \theta \,ds=\int_{0}^{L}\cos \left[\left(\right)^{2}\right]\,ds

한다면

{\displaystyles'= as}

그리고나서

ds={\frac {ds'}{a}

따라서

{\begin{aligned}x&={\frac {1}{a}}\int_{0}^{L'}\cos \left(s^{2}\right)\,ds\\y&=\int_{0}^{L}\sin \theta \,ds\\&=\int_{0}^{L}\sin \left[\left(\right)^{2}\right]\,ds\&={\frac {1}{a}\int_{0}^{L'}\sin \left ({s}^{2}\right)\,ds\end{aligned}

프레넬 적분의 팽창

정규화된 오일러 곡선의 경우인 $a$ = $1$ 이면 데카르트 좌표는 프레넬 적분(또는 오일러 적분)에 의해 다음과 같이 주어집니다.

{\begin{aligned}C(L)&=\int_{0}^{L}\cos \left(s^{2}\right)\,ds\\S(L)&=\int_{0}^{L}\sin \left(s^{2}\right)\,ds\end{aligned}

정규화

주어진 오일러 곡선의 경우:

2RL=2R_{c}L_{s}={\frac {1}{a^{2}}}

아니면

{\frac {1}{R}}={\frac {L}{R_{c}L_{s}}}=2a^{2}L

그리고나서

{\begin{aligned}x&={\frac {1}{a}}\int_{0}^{L'}\cos \left(s^{2}\right)\,ds\\y&={\frac {1}{a}\int_{0}^{L'}\sin \left(s^{2}\right)\,ds\end{aligned}}

어디에

{\begin{aligned}L'&=aL\\a&={\frac {1}{\sqrt {2R_{c}L_{s}}}}.\end{align}}

따라서 오일러 나선의 ( $x,$ y $)$ 해를 구하는 과정은 다음과 같이 설명할 수 있습니다.

정규화된 오일러 나선의 인자 $a$ ~ $L'$ 를 곱하여 원래 오일러 나선의 $지도$ L.
프레넬 적분에서 ( $x',$ y $')$ 를 구합니다.
요인 $1 / a$ 로 스케일링(비정규화)하여 ( $x',$ $y')$ 를 ( $x,$ y $')$ 에 매핑합니다. $참고$ 로1 $/a$ > 1.

정상화 과정에서

{\begin{aligned}R'_{c}&={\frac {R_{c}}{\sqrt {2R_{c}L_{s}}}}={\sqrt {\frac {R_{c}}{2L_{s}}}\\\L'_{s}&={\frac {L_{s}}{\sqrt {2R_{c}L_{s}}}}={\sqrt {\frac {L_{s}}{2R_{c}}}\end{align}

그리고나서

2R'_{c}L'_{s}=2{\sqrt {\frac {R_{c}}{2L_{s}}}}{\sqrt {\frac {L_{s}}{2R_{c}}}}={\frac {2}{2}}=1

일반적으로 정규화는 $L'$ 을 작은 값(1 미만)으로 감소시키고 몇 개의 항(특히 더 $큰$ θ 값의 경우 계산의 수치 불안정성이 증가하는 가격에서)으로 관리할 수 있는 프레넬 적분의 우수한 수렴 특성을 초래합니다.

일러스트레이션

주어진:

{\begin{aligned}R_{c}&=300\,\mathrm {m} \\L_{s}&=100\,\mathrm {m} \end{aligned}

그리고나서

\theta_{s}={\frac {L_{s}}{2R_{c}}}={\frac {100}{2\times 300}}={\frac {1}{6}}\ \mathrm {radian}

그리고.

2R_{c}L_{s}=60\,000

우리는 √60000, 즉 100 √6으로 오일러 나선을 다음을 갖는 정규화된 오일러 나선으로 축소합니다.

{\begin{aligned}R'_{c}&={\tfrac {3}{\sqrt {6}}}\,\mathrm {m} \\L'_{s}&={\tfrac {1}{\sqrt {6}}}\,\mathrm {m} \\2R'_{c}L'_{s}&=2\times {\tfrac {3}{\sqrt {6}}}\times {\tfrac {1}{\sqrt {6}}}\\&=1\end{aligned}}

그리고.

\theta_{s}={\frac {L'_{s}}{2R'_{c}}}={\frac {\frac {1}{\sqrt {6}}}{2\times {\frac {3}{\sqrt {6}}}}}={\frac {1}{6}}\ \mathrm {radian}

θ 두 개의 각도는 같습니다. 따라서 원래와 정규화된 오일러 나선이 기하학적으로 유사하다는 것을 확인할 수 있습니다. 정규화된 곡선의 위치는 프레넬 적분에서 결정할 수 있는 반면, 원래 오일러 나선의 위치는 스케일링 또는 정규화 해제를 통해 얻을 수 있습니다.

정규화된 오일러 나선의 다른 성질

정규화된 오일러 나선은 다음과 같이 표현할 수 있습니다.

{\begin{aligned}x&=\int_{0}^{L}\cos \left(s^{2}\right)\,ds\\y&=\int_{0}^{L}\sin \left(s^{2}\right)\,ds\end{aligned}

또는 멱급수로 표시됩니다.

{\begin{aligned}x&=\left.\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{(2i)!}}{\frac {s^{4i+1}}{4i+1}}\right _{0}^{L}&&=\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{(2i)!}}{\frac {L^{4i+1}}{4i+1}}\\y&=\left.\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{(2i+1)!}}{\frac {s^{4i+3}}{4i+3}}\right _{0}^{L}&&=\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{(2i+1)!}}{\frac {L^{4i+3}}{4i+3}}\end{aligned}}

정규화된 오일러 나선은 매개변수 L이 무한대에 접근함에 따라 극한의 한 점으로 수렴할 것이며, 이는 다음과 같이 표현할 수 있습니다.

{\begin{aligned}x^{\prime}&=\lim _{L\to \infty}\int_{0}^{L}\cos \left(s^{2}\right)\,ds&={\frac {1}{2}}\sqrt {\frac {\pi}{2}}\approx 0.6267\y^{\prime}&=\lim _{L\to \infty}\int_{0}^{L}\sin \left(s^{2}\right)\,ds&={\frac {1}{2}}\t\sqrt {\frac {\pi}{2}}\approx 0.6267\end{aligned}

정규화된 오일러 나선은 다음과 같은 성질을 갖습니다.

{\begin{aligned}2R_{c}L_{s}&=1\\\theta _{s}&={\frac {L_{s}}{2R_{c}}}=L_{s}^{2}\end{aligned}}

그리고.

{\begin{aligned}\theta &=\theta _{s}\cdot {\frac {L^{2}}{L_{s}^{2}}}=L^{2}\\{\frac {1}{R}}&={\frac {d\theta }{dL}}=2L\end{aligned}}

$2RL$ = $1$ 은또한 마지막 수학 문장과 일치하는 1/R = 2L을 의미합니다.

참고 항목

나선형 목록

참고문헌

^ Von Seggern, David H. (1994). Practical handbook of curve design and generation. Boca Raton, Fla.: CRC Press. ISBN 978-0-8493-8916-0.
^ ^a ^b ^c ^d ^e 레비앙, 라프. "오일러 나선: 수학사" 랩. 테크 (2008).
^ 마리 알프레드 코르누. M'ethode nouvelle pourla des problem des problem de diffraction dans le cas d'une on de cylindrique. Journal de Picicthéeoretique et applicquee, 1874년 5-15페이지.
^ Ziatdinov, R. (2012), "Family of superspirals with completely monotonic curvature given in terms of Gauss hypergeometric function", Computer Aided Geometric Design, 29 (7): 510–518
^ Constantin (2016-03-07). "The Clothoid". Pwayblog. Retrieved 2023-06-07.
^ Born, Max; Wolf, Emil (1993). Principles of optics: electromagnetic theory of propagation, interference and diffraction of light (6. ed., reprinted (with corrections) ed.). Oxford: Pergamon Press. ISBN 978-0-08-026481-3.
^ Eugene Hecht (1998). Optics (3rd ed.). Addison-Wesley. p. 491. ISBN 978-0-201-30425-1.
^ Kohtoku, M.; et al. (7 July 2005). "New Waveguide Fabrication Techniques for Next-generation PLCs" (PDF). NTT Technical Review. 3 (7): 37–41. Retrieved 24 January 2017.
^ Li, G.; et al. (11 May 2012). "Ultralow-loss, high-density SOI optical waveguide routing for macrochip interconnects". Optics Express. 20 (11): 12035–12039. Bibcode:2012OExpr..2012035L. doi:10.1364/OE.20.012035. PMID 22714189.
^ Cherchi, M.; et al. (18 July 2013). "Dramatic size reduction of waveguide bends on a micron-scale silicon photonic platform". Optics Express. 21 (15): 17814–17823. arXiv:1301.2197. Bibcode:2013OExpr..2117814C. doi:10.1364/OE.21.017814. PMID 23938654.
^ Unger, H.G. (September 1957). "Normal Mode Bends for Circular Electric Waves". The Bell System Technical Journal. 36 (5): 1292–1307. doi:10.1002/j.1538-7305.1957.tb01509.x.
^ Taylor, Edwin F.; Vokos, Stamatis; O’Meara, John M.; Thornber, Nora S. (1998-03-01). "Teaching Feynman's sum-over-paths quantum theory". Computers in Physics. 12 (2): 190–199. doi:10.1063/1.168652. ISSN 0894-1866.
^ Development, Paradigm Shift Driver; Brouillard, Adam (2016-03-18). The Perfect Corner: A Driver's Step-By-Step Guide to Finding Their Own Optimal Line Through the Physics of Racing. Paradigm Shift Motorsport Books. ISBN 9780997382426.
^ "Spiro".
^ " Spiro 0.01 release Typophile". www.typophile.com. Archived from the original on 2007-05-10.
^ Bartholdi, Laurent; Henriques, André (2012). "Orange Peels and Fresnel Integrals". The Mathematical Intelligencer. 34 (3): 1–3. arXiv:1202.3033. doi:10.1007/s00283-012-9304-1. ISSN 0343-6993. S2CID 52592272.
^ "A Strange Map Projection (Euler Spiral) - Numberphile". YouTube. Archived from the original on 2021-12-21.
^ Towal, R.B.; et al. (7 April 2011). "The Morphology of the Rat Vibrissal Array: A Model for Quantifying Spatiotemporal Patterns of Whisker-Object Contact". PLoS Computational Biology. 7 (4): e1001120. doi:10.1371/journal.pcbi.1001120. PMC 3072363. PMID 21490724.
Starostin, E.L.; et al. (15 January 2020). "The Euler spiral of rat whiskers". Science Advances. 6 (3): eaax5145. Bibcode:2020SciA....6.5145S. doi:10.1126/sciadv.aax5145. PMC 6962041. PMID 31998835.
^ Luo, Y.; Hartmann, M.J. (Jan 2023). "On the intrinsic curvature of animal whiskers". PLoS One. 18 (1): e0269210. doi:10.1371/journal.pone.0269210. PMC 9821693. PMID 36607960.

외부 링크

[1] Von Seggern, David H. (1994). Practical handbook of curve design and generation. Boca Raton, Fla.: CRC Press. ISBN 978-0-8493-8916-0.

[LevienHistory-2] 레비앙, 라프. "오일러 나선: 수학사" 랩. 테크 (2008).

[3] 마리 알프레드 코르누. M'ethode nouvelle pourla des problem des problem de diffraction dans le cas d'une on de cylindrique. Journal de Picicthéeoretique et applicquee, 1874년 5-15페이지.

[4] Ziatdinov, R. (2012), "Family of superspirals with completely monotonic curvature given in terms of Gauss hypergeometric function", Computer Aided Geometric Design, 29 (7): 510–518

[pwayblog-5] Constantin (2016-03-07). "The Clothoid". Pwayblog. Retrieved 2023-06-07.

[6] Born, Max; Wolf, Emil (1993). Principles of optics: electromagnetic theory of propagation, interference and diffraction of light (6. ed., reprinted (with corrections) ed.). Oxford: Pergamon Press. ISBN 978-0-08-026481-3.

[Hecht-7] Eugene Hecht (1998). Optics (3rd ed.). Addison-Wesley. p. 491. ISBN 978-0-201-30425-1.

[8] Kohtoku, M.; et al. (7 July 2005). "New Waveguide Fabrication Techniques for Next-generation PLCs" (PDF). NTT Technical Review. 3 (7): 37–41. Retrieved 24 January 2017.

[9] Li, G.; et al. (11 May 2012). "Ultralow-loss, high-density SOI optical waveguide routing for macrochip interconnects". Optics Express. 20 (11): 12035–12039. Bibcode:2012OExpr..2012035L. doi:10.1364/OE.20.012035. PMID 22714189.

[10] Cherchi, M.; et al. (18 July 2013). "Dramatic size reduction of waveguide bends on a micron-scale silicon photonic platform". Optics Express. 21 (15): 17814–17823. arXiv:1301.2197. Bibcode:2013OExpr..2117814C. doi:10.1364/OE.21.017814. PMID 23938654.

[11] Unger, H.G. (September 1957). "Normal Mode Bends for Circular Electric Waves". The Bell System Technical Journal. 36 (5): 1292–1307. doi:10.1002/j.1538-7305.1957.tb01509.x.

[12] Taylor, Edwin F.; Vokos, Stamatis; O’Meara, John M.; Thornber, Nora S. (1998-03-01). "Teaching Feynman's sum-over-paths quantum theory". Computers in Physics. 12 (2): 190–199. doi:10.1063/1.168652. ISSN 0894-1866.

[13] Development, Paradigm Shift Driver; Brouillard, Adam (2016-03-18). The Perfect Corner: A Driver's Step-By-Step Guide to Finding Their Own Optimal Line Through the Physics of Racing. Paradigm Shift Motorsport Books. ISBN 9780997382426.

[14] "Spiro".

[15] " Spiro 0.01 release Typophile". www.typophile.com. Archived from the original on 2007-05-10.

[16] Bartholdi, Laurent; Henriques, André (2012). "Orange Peels and Fresnel Integrals". The Mathematical Intelligencer. 34 (3): 1–3. arXiv:1202.3033. doi:10.1007/s00283-012-9304-1. ISSN 0343-6993. S2CID 52592272.

[:0-17] "A Strange Map Projection (Euler Spiral) - Numberphile". YouTube. Archived from the original on 2021-12-21.

[18] Towal, R.B.; et al. (7 April 2011). "The Morphology of the Rat Vibrissal Array: A Model for Quantifying Spatiotemporal Patterns of Whisker-Object Contact". PLoS Computational Biology. 7 (4): e1001120. doi:10.1371/journal.pcbi.1001120. PMC 3072363. PMID 21490724.
Starostin, E.L.; et al. (15 January 2020). "The Euler spiral of rat whiskers". Science Advances. 6 (3): eaax5145. Bibcode:2020SciA....6.5145S. doi:10.1126/sciadv.aax5145. PMC 6962041. PMID 31998835.

[19] Luo, Y.; Hartmann, M.J. (Jan 2023). "On the intrinsic curvature of animal whiskers". PLoS One. 18 (1): e0269210. doi:10.1371/journal.pone.0269210. PMC 9821693. PMID 36607960.

[1]

[2]

[3]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

Search

오일러 나선

네임스페이스

더

목차

역사

적용들

추적 전이곡선

광학

통합광학

파인만 경로 적분

자동차 경주

타이포그래피 및 디지털 벡터 도면

지도투영

거품기 모양

공식화

기호

프레넬 적분의 팽창

정규화

일러스트레이션

정규화된 오일러 나선의 다른 성질

참고 항목

참고문헌

더보기

외부 링크