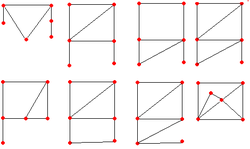
비대칭 그래프

Asymmetric graph
8개의 6-Vertex 비대칭 그래프
5개의 가장 작은 비대칭 입방 그래프 중 하나인 Frucht 그래프.
자동화에 의해 정의된 그래프 패밀리
거리 변환의 → 거리 규칙의 ← 매우 규칙적인.
↓
대칭(대칭 변환) ← t-변환, t ≥ 2 꼬불꼬불한
↓
(연결된 경우)
정점 및 에지 변환 		→ 가장자리-변환적이고 규칙적인 → 가장자리-변환성
↓ ↓ ↓
정점 변환의 → 정칙의 → (양립할 경우)
복엽의
↑
케이리 그래프 ← 무궤도적 비대칭의

수학의 한 분야인 그래프 이론에서 비직교 대칭이 없으면 비대칭 그래프라고 한다.

형식적으로 그래프의 자동형성은 p(u)와 p(v)가 인접한 경우에만 어떤 두 꼭지점 u와 v가 인접하는 속성과 그 정점의 순열 p이다.그래프의 정체성 매핑 자체가 항상 자동형이며, 그래프의 사소한 자동형성이라고 불린다.비대칭 그래프는 다른 자동화가 없는 그래프다.

예

가장 작은 비대칭 그래프에는 6개의 정점이 있다.[1]가장 작은 비대칭 정규 그래프에는 10개의 꼭지점이 있는데, 4개의 정규 그래프와 5개의 정규 그래프가 있다.[2][3]5개의 가장 작은 비대칭 입방형 그래프[4] 중 하나는 1939년에 발견된 12Vx Frucht 그래프다.[5]Frucht의 정리의 강화된 버전에 따르면, 무한히 많은 비대칭 입방 그래프가 있다.

특성.

비대칭 그래프의 클래스는 보완 하에서 닫힌다. 즉, 그래프 G는 보완이 있는 경우에만 비대칭이다.[1]모든 n-vertex 비대칭 그래프는 최대 n/2 + o(n) 에지를 추가하고 제거하여 대칭으로 만들 수 있다.[1]

랜덤 그래프

n 정점에서의 그래프 비율은 n이 증가함에 따라 0이 되는 경향이 있는데, 이것은 비공식적으로 "거의 모든 유한한 그래프는 비대칭"으로 표현된다.이와는 대조적으로, 비공식적으로, "대부분의 모든 무한 그래프들은 대칭이다."좀 더 구체적으로, Erdss-Rényi 모델에서 카운트 가능한 무한 랜덤 그래프는 확률 1과 함께 매우 대칭적인 Rado 그래프에 대해 이형성이 있다.[1]

나무들

가장 작은 비대칭 트리는 7개의 꼭지점을 가지고 있다: 그것은 길이가 1, 2, 3이고 공통의 끝점에 연결되어 있는 세 개의 경로로 구성되어 있다.[6]그래프의 상황과 대조적으로 거의 모든 나무들은 대칭이다.특히, n개의 라벨이 붙은 노드의 모든 트리 중에서 나무를 무작위로 선택한 다음, n이 증가함에 따라 1이 될 확률로, 트리는 동일한 노드에 인접한 두 개의 잎을 포함하고 이 두 잎을 교환하는 대칭을 가질 것이다.[1]

참조

  1. ^ a b c d e Erdős, P.; Rényi, A. (1963), "Asymmetric graphs" (PDF), Acta Mathematica Hungarica, 14 (3): 295–315, doi:10.1007/BF01895716, archived from the original (PDF) on 2017-07-06, retrieved 2010-04-22.
  2. ^ Baron, G.; Imrich, W. (1969), "Asymmetrische reguläre Graphen", Acta Mathematica Academiae Scientiarum Hungaricae, 20: 135–142, doi:10.1007/BF01894574, MR 0238726.
  3. ^ Gewirtz, Allan; Hill, Anthony; Quintas, Louis V. (1969), "The minimal number of points for regular asymmetric graphs", Universidad Técnica Federico Santa Maria. Scientia, 138: 103–111, MR 0266818.
  4. ^ Bussemaker, F. C.; Cobeljic, S.; Cvetkovic, D. M.; Seidel, J. J. (1976), Computer investigation of cubic graphs, EUT report, vol. 76-WSK-01, Dept. of Mathematics and Computing Science, Eindhoven University of Technology
  5. ^ Frucht, R. (1939), "Herstellung von Graphen mit vorgegebener abstrakter Gruppe.", Compositio Mathematica (in German), 6: 239–250, ISSN 0010-437X, Zbl 0020.07804.
  6. ^ Quintas, Louis V. (1967), "Extrema concerning asymmetric graphs", Journal of Combinatorial Theory, 3 (1): 57–82, doi:10.1016/S0021-9800(67)80018-8.