카운트 가능 집합

수학에서 집합은 자연수 집합 N = {0, 1, 2, 3, ...^[a]의 일부 부분집합과 같은 카디널리티(집합된 요소의 수)를 갖는다면 셀 수 있다.따라서 집합 S는 S에서 N까지의 주입함수 f : S → N이 존재한다면 셀 수 있다.그것은 단순히 S 내의 모든 원소가 서로 다르다는 것을 의미한다.

카운트 가능 집합은 유한 집합 또는 카운트 가능 무한 집합 중 하나입니다.유한이든 무한이든 카운트 가능한 집합의 요소는 항상 한 번에 하나씩 카운트할 수 있습니다. 카운트되는 요소의 수가 무한하기 때문에 카운트가 완료되지 않을 수 있지만 집합의 모든 요소는 고유한 자연수와 관련지어집니다.

Georg Cantor는 셀 수 있는 집합과 셀 수 없는 집합의 대조를 이루는 집합의 개념을 도입했습니다.오늘날, 계산 가능한 집합은 이산 수학이라고 불리는 수학의 한 분야를 형성한다.

용어에 관한 주의사항

여기서 정의한 '계수 가능'과 '계수 가능 무한'이라는 용어는 매우 흔하지만,^[1] 이 용어는 보편적이지 않습니다.다른 스타일은 셀 수 있을 정도로 무한하다고 불리는 것을 의미하며, 셀 수 있을 정도로 셀 수 있을 수 있는 것은 셀 수 있는 것을 셀 수 있는 것은 셀 ^[2]^[3]수 있는 것입니다.애매모호함을 피하기 위해 "가장 셀 수 있는" 용어와 "세어볼 수 있는 무한" 용어로 스스로를 제한할 수 있다. 비록 모순에 관해서는 이것이 양쪽 세계 ^{[citation needed]}중 가장 나쁜 것이다.독자는 문헌에서 "계수 가능"이라는 용어를 접했을 때 사용 중인 정의를 확인할 것을 권장합니다.

열거형^[4] 및 부인형이라는^[5]^[6] 용어는 예를 들어 각각 ^[7]계산 가능 및 계산 가능 무한을 지칭하는 말로도 사용될 수 있지만, 정의가 다양하므로 ^[8]사용 중인 정의를 다시 한 번 점검할 것을 독자에게 권고한다.

정의.

가장 간결한 정의는 카디널리티에 관한 것이다. $집합$ S는 그 카디널리티 S가 자연수 집합 N의 카디널리티인 $($ 알레프 $)$ 이하일 때 $카운트$ 할 수 있다. $집합$ S는 $|S|=\aleph _{0}$ 0(\ $displaystyle$ S $=\aleph_$ })이면 카운트할 수 없다.§ $(\$ ; 자세한 내용은 ^[9]Uncountable set를 참조하십시오.

모든 $집합$ S에 대해 다음 명제는 동일합니다.

$S$ 는 셀 ^[5]수 있다.
$S$ 에서 ^[10]^[11]N까지 주입 함수가 존재합니다.
$S$ 가 비어 있거나 N에서 ^[11] $S$ 까지의 투영 함수가 있습니다.
S와 ^[12]N의 서브셋 $사이$ 에는 바이젝티브 매핑이 존재합니다.
$S$ 는 유한하거나 셀 수 있을 정도로 ^[13]무한하다.

마찬가지로 다음 명제는 동일합니다.

$S$ 는 셀 수 있을 정도로 무한하다.
S와 N $사이$ 에는 주입형 및 주관형(따라서 비주사형) 매핑이 있습니다.
$S$ 는 ^[14]N과 일대일로 대응한다.
S의 $요소$ 는 $a_{0},a_{1},a_{2},\ldots$ $a_{0},a_{1},a_{2},\ldots$ a $a_{0},a_{1},a_{2},\ldots$ , $a_{0},a_{1},a_{2},\ldots$ 2, $…({displaystyle a_{0}, a_{1}, a_{2},\ldots$ })의 $무한$ $a_{0},a_{1},a_{2},\ldots$ 로 배열할 수 있습니다. $여기$ 서 i ${$ $displaystyle$ $a_{$ j $a_{j}$ }는 i{j}의 $a_{j}$ ${$ $displaystyle$ i $\neq}$ 와 $a_{i}$ $i\neq j$ 구별됩니다.^[15]^[16]

역사

1874년, 그의 첫 집합론 기사에서, 칸토르는 실수의 집합이 셀 수 없다는 것을 증명했고, 따라서 모든 무한 집합이 셀 ^[17]수 있는 것은 아니라는 것을 보여준다.1878년,^[18] 그는 추기경을 정의하고 비교하기 위해 일대일로 대응했다.1883년, 그는 그의 무한 서수로 자연수를 확장했고, 다른 무한 ^[19]기수를 가진 무한 집합을 만들기 위해 서수 집합을 사용했습니다.

서론

세트는 요소의 집합이며 여러 가지 방법으로 설명할 수 있습니다.한 가지 방법은 단순히 모든 요소를 나열하는 것입니다. 예를 들어, 정수 3, 4, 5로 구성된 세트를 {3, 4, 5} 로스터 ^[20]형식이라고 할 수 있습니다.그러나 이것은 작은 세트에만 유효합니다.큰 세트에 대해서는 시간이 많이 걸리고 오류가 발생하기 쉽습니다.모든 요소를 나열하는 대신, 때때로 줄임표("...")가 세트 내의 시작 요소와 끝 요소 사이에 많은 요소를 나타내기 위해 사용됩니다.독자가 쉽게 추측할 수 있다고 믿는 경우...는 를 나타냅니다.예를 들어 {1, 2, 3, ..., 100}은 1 ~100의 정수 집합을 나타냅니다.그러나 이 경우에도 집합 내의 요소 수는 유한하기 때문에 모든 요소를 나열할 수 있습니다.

일부 집합은 무한합니다.이 집합에는 n개 이상의 요소가 있습니다.여기서 n은 지정할 수 있는 정수입니다.(n = $9 \times 10과 32$ $같이$ 지정된 정수 n이 아무리 크더라도 무한 집합에는 n개 이상의 요소가 있습니다.)예를 들어 {0, 1, 2, 3, 4, 5, ...}^[a]로 표시할 수 있는 자연수 집합에는 무한히 많은 원소가 포함되어 있으므로 자연수를 사용하여 크기를 지정할 수 없습니다.그럼에도 불구하고 무한 집합은 크기(또는 더 적절하게는 카디널리티, 세트 내의 요소 수에 대한 기술 용어)에 대한 명확한 개념을 가지고 있으며 모든 무한 집합이 동일한 카디널리티를 갖는 것은 아닙니다.

정수에서 짝수로의 바이젝티브 매핑

이것이 무엇을 의미하는지 이해하기 위해 먼저 그것이 무엇을 의미하지 않는지 살펴봅니다.예를 들어, 홀수 정수가 무한히 많고 짝수 정수가 무한히 많으며, 따라서 전체적으로는 무한히 많은 정수가 있습니다.그러나 홀수 정수와 같은 짝수 정수의 개수도 전체 정수의 개수와 같은 것으로 나타났습니다.이는 모든 정수에 대해 고유한 짝수 정수가 존재하도록 배열할 수 있기 때문입니다.

\displaystyle \ldots \!-\!2\!\rightarrow \!-\!4,-,\!1\!\rightarrow \!0,1,0!\rightarrow \!2,2\!\rightarrow \!4,\cdots 。

또는 일반적으로 n

n\rightarrow 2n

(표시

스타일 n\

오른쪽 화살표 2n)

입니다(그림 참조).여기서는 정수와 짝수의 정수를 1 대 1 대응(또는 분사)으로 배열했습니다.이것은 각 집합의 각 요소가 다른 집합의 단일 요소에 대응하도록 두 집합 사이를 매핑하는 함수입니다.

단, 모든 무한 집합이 동일한 카디널리티를 갖는 것은 아닙니다.예를 들어, Georg Cantor(이 개념을 도입한)는 실수가 자연수(부정수가 아닌 정수)와 일대일로 대응될 수 없으므로, 실수의 집합이 자연수의 집합보다 더 큰 카디널리티를 갖는다는 것을 증명했다.

정식 개요

정의상, 집합 S는 S에서 자연수 N = {0, 1, 2, 3, ...}까지의 주입 함수 f : S → N이 존재한다면 셀 수 있다.이는 단순히 S의 모든 원소가 N의 다른 원소와 대응한다는 것을 의미합니다.

세트를 다른 클래스로 분할하는 것은 당연하다고 생각할 수 있습니다.하나의 요소를 포함한 모든 세트를 함께 배치하고, 2개의 요소를 포함한 모든 세트를 함께 배치하고, 마지막으로 모든 무한 집합을 조합하여 같은 크기를 갖는 것으로 간주합니다.그러나 이 견해는 크기의 자연적 정의로는 옹호할 수 없다.

이것을 자세히 설명하려면, 우리는 바이오젝션의 개념이 필요하다.비록 "분사"가 숫자보다 더 발전된 개념으로 보일지라도, 집합론의 관점에서 수학의 일반적인 발전은 훨씬 더 단순한 집합에 기초하기 때문에 숫자 앞에 함수를 정의한다.여기서 바이젝션의 개념이 도입됩니다: 대응 관계를 정의합니다.

a ↔ 1, b ↔ 2, c ↔ 3

{a, b, c}의 모든 요소는 {1, 2, 3)의 한 요소와 정확히 쌍을 이루며, 그 반대도 마찬가지이므로 분사를 정의합니다.

이제 이 상황을 일반화하고, 두 세트 사이에 분사가 있는 경우에만 두 세트의 크기가 동일하다고 정의합니다.모든 유한 집합에서, 이것은 "같은 크기"에 대한 일반적인 정의를 제공합니다.

무한 집합의 경우, A = {1, 2, 3, ...}, B = {2, 4, 6, ...}, 짝수 정수의 집합이라고 하자.정의상 이들 집합은 크기가 같기 때문에 B는 무한하다고 주장합니다.이걸 증명하려면 그들 사이에 분사를 보여줘야 한다는 걸 명심해이것은 할당 n ↔ 2n을 사용하여 달성할 수 있습니다. 따라서 다음과 같이

1 ↔ 2, 2 ↔ 4, 3 ↔ 6, 4 ↔ 8, ....

앞의 예시와 같이 A의 모든 요소는 B의 한 요소와 정확히 쌍을 이루며, 그 반대도 마찬가지입니다.그래서 같은 사이즈를 가지고 있습니다.이것은 적절한 서브셋 중 하나와 같은 크기의 집합의 예입니다.이것은 유한 집합에서는 불가능합니다.

마찬가지로, 자연수의 모든 순서쌍의 집합(자연수의 두 집합의 데카르트 곱, N × N)은 그림에 있는 것과 같은 경로를 따라가는 것으로 알 수 있듯이 셀 수 있을 정도로 무한하다.

칸토어 페어링 기능은 각 자연수 쌍에 하나의 자연수를 할당합니다.

결과 매핑은 다음과 같이 진행됩니다.

0 ↔ (0, 0), 1 ↔ (1, 0), 2 ↔ (0, 1), 3 ↔ (2, 0), 4 ↔ (1, 1), 5 ↔ (0, 2), 6 ↔ (3, 0), ....

이 매핑에는 이러한 순서쌍이 모두 포함됩니다.

이 삼각형 매핑 형식은 n-튜플의 처음 두 요소를 자연수에 반복적으로 매핑함으로써 자연수의 n-튜플(a₁, a₂, a₃, ..., a_n)로_i 재귀적으로 일반화한다.예를 들어 (0, 2, 3)은 (0, 2)로 쓸 수 있습니다.다음으로 (0, 2)는 5에 매핑되므로 (0, 2)는 (5, 3)에 매핑되고 (5, 3)는 39에 매핑됩니다.(a, b)와 같은 쌍이 다른 자연수에 매핑되므로 단일 요소에 의한 2개의 n개의 튜플의 차이는 n개의 튜플을 다른 자연수에 매핑하기에 충분하다.따라서 n-튜플 집합에서 자연수 N 집합으로의 주입이 증명된다.데카르트 곱에 의해 만들어진 n-튜플의 집합은 각 튜플의 각 원소는 자연수에 대응하므로 모든 튜플을 자연수로 쓸 수 있으며, 그 후 동일한 논리를 적용하여 정리를 증명한다.

정리 — 계산 가능한 집합의 데카르트 곱은 셀 ^[21]^[b]수 있습니다.

모든 정수 Z의 집합과 모든 유리수 Q의 집합은 직관적으로 N보다 훨씬 커 보일 수 있습니다. 그러나 겉모습은 속일 수 있습니다.만약 쌍이 저속분수(a와 b as 0이 정수인 a/b 형태의 분수)의 분자와 분모로 처리된다면, 우리는 모든 양의 분수에 대해 그에 대응하는 뚜렷한 자연수를 얻을 수 있다.모든 자연수는 N/1의 분수이기 때문에 이 표현에는 자연수도 포함됩니다.그래서 우리는 양의 정수만큼 정확히 양의 유리수가 있다는 결론을 내릴 수 있습니다.이는 아래에서 볼 수 있듯이 모든 유리수에 대해서도 해당된다.

정리 - Z(모든 정수의 집합)와 Q(모든 유리수의 집합)는 셀 ^[c]수 있습니다.

마찬가지로 대수적 숫자의 집합은 셀 ^[23]^[d]수 있다.

경우에 따라서는 복수의 매핑이 도움이 되는 경우가 있습니다.카운터블로 표시되는 세트A는 다른 세트B에 1대1로 매핑(주입)되며, B가 자연수 세트에 1대1로 매핑된 경우 A는 카운터블로 증명됩니다.예를 들어, p/q는 (p, q)에 매핑되기 때문에 양의 유리수 집합은 자연수 쌍 집합(2-튜플)에 일대일로 쉽게 매핑될 수 있습니다.자연수 쌍의 집합은 위와 같이 자연수 집합에 일대일로 매핑되므로(실제로 일대일 대응 또는 바이젝션) 양의 유리수 집합은 셀 수 있는 것으로 증명됩니다.

정리 - 계산 가능한 집합의 유한 합집합은 모두 ^[24]^[25]^[e]계산 가능합니다.

셀 수 없는 집합이 있다는 것을 아는 선견지명이 있기 때문에, 우리는 이 마지막 결과를 더 이상 추진할 수 있을지 궁금할 수 있다.대답은 "예"와 "아니오"입니다. 우리는 그것을 확장할 수 있지만, 우리는 그렇게 하기 위해 새로운 공리를 가정할 필요가 있습니다.

정리 - (계산 가능한 선택 공리 가정)셀 수 있는 많은 집합의 합은 셀 ^[f]수 있다.

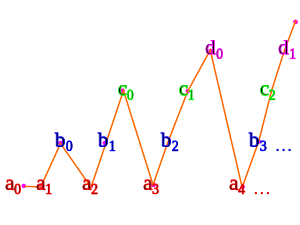
예를 들어 카운트 가능한 집합 a, b, c, ...가 지정됩니다.

셀 수 있는 집합 수에 대한 열거형입니다.

위에서 살펴본 삼각 열거의 변형을 사용하여:

0에₀ 대한 지도
1에₁ 대한 지도
b는₀ 2에 매핑됩니다.
3에₂ 대한 지도
b는₁ 4에 매핑됩니다.
c는₀ 5에 매핑됩니다.
6에₃ 대한 지도
b는₂ 7에 매핑됩니다.
c는₁ 8에 매핑됩니다.
d는₀ 9에 맵됩니다.
10에₄ 대한 지도
...

이것은 세트 a, b, c, ...가 분리되었을 경우에만 기능합니다.그렇지 않다면, 합집합은 더 작기 때문에 이전의 정리로도 계산할 수 있다.

모든 집합 a, b, c, ...을 동시에 색인화하기 위해서는 계산 가능한 선택 공리가 필요하다.

정리 — 자연수의 모든 유한 길이 시퀀스의 집합은 셀 수 있습니다.

이 세트는 길이-1 시퀀스, 길이-2 시퀀스, 길이-3 시퀀스의 결합이며, 각각이 계수 가능한 세트입니다(확정 데카르트 곱).그래서 우리는 이전의 정리에 의해 셀 수 있는 집합의 계수 가능한 합집합에 대해 이야기하고 있습니다.

정리 — 자연수의 모든 유한 부분 집합의 집합은 셀 수 있습니다.

유한 서브셋의 요소는 유한 시퀀스로 정렬할 수 있습니다.유한 시퀀스는 셀 수 있을 정도로 많으므로 유한 서브셋은 셀 수 없을 정도로 많습니다.

정리: S와 T를 세트 합니다.

함수 f : S → T가 injective이고 T가 countable이면 S는 countable이다.
함수 g : S → T가 사사형이고 S가 계수형이면 T는 계수형이다.

이는 주입/^[g]주사 함수로 계산 가능한 집합의 정의에서 비롯됩니다.

칸토어의 정리는 만약 A가 집합이고 P(A)가 그것의 거듭제곱 집합, 즉 A의 모든 부분 집합의 집합이라면, A에서 P(A)까지는 어떠한 주관함수도 존재하지 않는다고 주장한다.칸토어의 정리에 증거가 있다.이것과 위의 기본정리의 직접적인 결과로서 다음과 같은 것이 있습니다.

제안 - 집합 P(N)는 계산할 수 없습니다. 즉, 셀 수 없습니다.

이 결과에 대한 자세한 내용은 칸토어의 대각선 논거를 참조하십시오.

실수의 집합은 셀 ^[h]수 없고, 자연수의 모든 무한 수열의 집합도 셀 수 없습니다.

집합론의 최소 모델은 셀 수 있다.

ZFC 집합론의 표준 모델(내부 모델 참조)인 집합이 있으면 최소 표준 모델(구성 가능한 우주 참조)이 있습니다.뢰벤하임-스콜렘 정리는 이 최소 모델이 셀 수 있다는 것을 보여주기 위해 사용될 수 있다."산출 불가"라는 개념은 이 모델에서도 타당하며, 특히 이 모델 M에는 다음과 같은 요소가 포함되어 있습니다.

M의 서브셋(따라서 셀 수 있음)
M의 관점에서 보면 셀 수 없을 정도로

집합론의 초기에는 역설적으로 여겨졌었다. 자세한 내용은 스콜렘의 역설에서 볼 수 있다.

최소 표준 모델은 다른 많은 종류의 수뿐만 아니라 모든 대수적 숫자와 효과적으로 계산할 수 있는 초월수를 포함합니다.

총주문수

카운트 가능한 집합은 다음과 같이 다양한 방법으로 정렬할 수 있습니다.

순서(서수 번호 참조):
- 자연수의 일반적인 순서(0, 1, 2, 3, 4, 5, ...)
- 순서의 정수(0, 1, 2, 3, ...; -1, -2, -3, ...)
기타(잘 주문되지 않음):
- 정수의 일반적인 순서(..., -3, -2, -1, 0, 1, 2, 3, ...)
- 일반적인 유리 번호 순서(순서 목록으로 명시적으로 쓸 수 없습니다!)

여기서의 우물 순서 두 가지 예에서 모든 부분 집합은 최소 요소를 가집니다. 또한 두 가지 비 우물 순서 모두에서 일부 부분 집합은 최소 요소를 가지지 않습니다.이는 전체 주문이 양호한 주문인지 여부를 결정하는 핵심 정의입니다.

「」를 참조해 주세요.

메모들

^ ^a ^b $N$ 과 N*= { $1, 2, 3$ , $...}$ $사이$ 에는 분명한 분사가 있기 때문에 0을 자연수로 간주하든 그렇지 않든 아무런 차이가 없다.어느 경우든, 이 기사는 ISO 31-11과 0을 자연수로 하는 수학 논리학의 표준 규약을 따르고 있습니다.
^ 증명: f $(m,$ $n)$ = $23$ 에^mⁿ $의해$ $주어진$ 함수 f : $N$ × $N$ → N은 ^[22]주입식이기 때문에 정의의 결과로 $계산$ 될 $수$ $있음$ 을 관찰한다.그런 다음 두 개의 계수 집합의 데카르트 곱은 계수할 수 있다. 왜냐하면 $A$ 와 B가 계수할 수 있는 두 집합이면 $제외$ $f$ : $N$ → $A$ 와g : $N$ → $B$ 가 존재하기 때문이다.그래서...
$f \times g : N \times N \to A \times B$

는 가산 가능한 $집합$ N × $N$ 에서 $집합$ A × $B$ 로의 돌출이며, 결과는 A × $B$ 가 가산 가능한 것을 $의미$ 한다.이 결과는 계산 가능한 집합의 유한 집합의 데카르트 곱으로 일반화되며, 그 증거는 집합의 집합 수에 대한 유도에 따른다.
^ 증명: $n$ 이 음이 아니면 f( $n$ ) = $2$ 로ⁿ $주어지는$ 함수 $f$ : $Z$ → N, n이 음이면 $f$ $(n)$ = $3$ 으로⁻ⁿ 주어지는 함수 f : Z는 셀 수 있다.g $(m,$ $n)$ = $m /(n +$ 1)에 $의해$ 주어진 $함수$ g : $Z$ × $N$ → $Q$ 는 계수 $집합$ Z × $N$ 에서 $유리$ Q로의 돌출이기 때문에 계수할 수 $있다$ .
^ 증명: 정의에 따르면, 모든 대수적 수(복소수 포함)는 정수 계수를 갖는 다항식의 근입니다.대수 $({displaystyle \alpha$ 를 지정하면 0 $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ + $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ + $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ + $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ + $({$ )로 $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ . $}x^{1}+a_{2$ $}x^{2}+\cdots$ + $a_{n$ $}$ x $^{$ n $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ }}은 $\alpha$ (는) $정수$ 계수를 갖는 다항식입니다 $.$ $α$ 는 다항식의 k번째 루트이며, 여기서 루트는 작은 것부터 큰 것까지 절대값으로 정렬된 다음 작은 것부터 큰 것까지 인수로 정렬됩니다.f $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $k$ - $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ → $3$ a 0 $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ a $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ 7 $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ p $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ + $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ n $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ { $display f$ ( \ $alpha$ ) = $2$ p k - 1 → 2 $cdot$ 3 $^{a _$ 0 } \ $cdot 5$ ^ { 1 }에 $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ 주어지는 주입(즉, 일대일) 함수 f : $A$ → Q)를 정의할 수 있다.
^ 증명: A가 I={1, ...,n}의 각 i에 대해 계수 가능한 $집합$ 이라면_i, $각$ n에 대해 $사사함수 i$ $g :$ $N i$ → A가 존재하며, 따라서 함수는 $G:I\times \mathbf {N} \to \bigcup _{i\in I}A_{i$ G $(i,$ $m)$ = $g i (m)$ 로 주어지는 는 굴절이다.I × $N$ 은 계수 $가능$ 하므로 합집합 ${\textstyle \bigcup _{i\in I}A_{i}}$ i ${\textstyle \bigcup _{i\in I}A_{i}}$ I ${\textstyle \bigcup _{i\in I}A_{i}}$ \ $textstyle$ \ $bigcup$ _ ${ i$ \ $in$ I } $A$ _ { $i$ }는 ${\textstyle \bigcup _{i\in I}A_{i}}$ 계수 가능합니다.
^ 증명: 유한한 경우와 마찬가지로 I=N과 우리는 N의 $각$ $i$ 에 대해 $N$ 에서 $A$ 까지의_i 사출의 빈 집합에서 $사출 i$ g를 선택하기 위해 계산 가능한 선택 공리를 사용한다.
^ 증명: (1) T가 계수 가능한 경우 주입 함수 h : T → N이 있음을 관찰하고, f : S → T가 주사인 경우 조성물 h o f : S → N이 주사되므로 S는 계수 가능하다.(2) S가 셀 수 있는 경우 S가 비어 있거나 surjective 함수 h : N → S가 있는지 관찰한다.g : S → T이면 S와 T가 모두 비어 있거나 g o h : N → T의 조성이 surjective이다.어느 경우든 T는 셀 수 있다.
^ 토폴로지 증명은 Cantor의 첫 번째 불가산성 증명과 유한 교차로 속성#응용 프로그램을 참조하십시오.

인용문

^ Manetti, Marco (19 June 2015). Topology. Springer. p. 26. ISBN 978-3-319-16958-3.
^ 루딘 1976, 제2장
^ 타오 2016, 181페이지
^ 캄케 1950, 2페이지
^ ^a ^b 제1장 제2장 Lang 1993
^ 아포톨 1969, 23페이지, 1.14장
^ Thierry, Vialar (4 April 2017). Handbook of Mathematics. BoD - Books on Demand. p. 24. ISBN 978-2-9551990-1-5.
^ Mukherjee, Subir Kumar (2009). First Course in Real Analysis. Academic Publishers. p. 22. ISBN 978-81-89781-90-3.
^ Yaqub, Aladdin M. (24 October 2014). An Introduction to Metalogic. Broadview Press. ISBN 978-1-4604-0244-3.
^ Singh, Tej Bahadur (17 May 2019). Introduction to Topology. Springer. p. 422. ISBN 978-981-13-6954-4.
^ ^a ^b Katzourakis, Nikolaos; Varvaruca, Eugen (2 January 2018). An Illustrative Introduction to Modern Analysis. CRC Press. ISBN 978-1-351-76532-9.
^ Halmos 1960, 페이지 91
^ Weisstein, Eric W. "Countable Set". mathworld.wolfram.com. Retrieved 2020-09-06.
^ 캄케 1950, 2페이지
^ Dlab, Vlastimil; Williams, Kenneth S. (9 June 2020). Invitation To Algebra: A Resource Compendium For Teachers, Advanced Undergraduate Students And Graduate Students In Mathematics. World Scientific. p. 8. ISBN 978-981-12-1999-3.
^ 타오 2016, 182페이지
^ Stillwell, John C. (2010), Roads to Infinity: The Mathematics of Truth and Proof, CRC Press, p. 10, ISBN 9781439865507, Cantor's discovery of uncountable sets in 1874 was one of the most unexpected events in the history of mathematics. Before 1874, infinity was not even considered a legitimate mathematical subject by most people, so the need to distinguish between countable and uncountable infinities could not have been imagined.
^ 칸토르 1878 페이지 242
^ Ferreiros 2007, 268페이지, 272-273.
^ "What Are Sets and Roster Form?". expii. 2021-05-09. Archived from the original on 2020-09-18.
^ Halmos 1960, 페이지 92
^ 아벨스고르 1990, 182페이지
^ 캄케 1950, 3~4페이지
^ Avelsgaard 1990, 페이지 180
^ Fletcher & Patty 1988, 187페이지

레퍼런스

Apostol, Tom M. (June 1969), Multi-Variable Calculus and Linear Algebra with Applications, Calculus, vol. 2 (2nd ed.), New York: John Wiley + Sons, ISBN 978-0-471-00007-5
Avelsgaard, Carol (1990), Foundations for Advanced Mathematics, Scott, Foresman and Company, ISBN 0-673-38152-8
Cantor, Georg (1878), "Ein Beitrag zur Mannigfaltigkeitslehre", Journal für die Reine und Angewandte Mathematik, 1878 (84): 242–248, doi:10.1515/crelle-1878-18788413
Ferreirós, José (2007), Labyrinth of Thought: A History of Set Theory and Its Role in Mathematical Thought (2nd revised ed.), Birkhäuser, ISBN 978-3-7643-8349-7
Fletcher, Peter; Patty, C. Wayne (1988), Foundations of Higher Mathematics, Boston: PWS-KENT Publishing Company, ISBN 0-87150-164-3
Halmos, Paul R. (1960), Naive Set Theory, D. Van Nostrand Company, Inc 1974년 뉴욕주 스프링거-발락에서 전재.ISBN 0-387-90092-6(스프링거-버래그 에디션).마르티노 파인북스 전재, 2011.ISBN 978-1-61427-131-4(페이퍼백판).
Kamke, Erich (1950), Theory of Sets, Dover series in mathematics and physics, New York: Dover, ISBN 978-0486601410
Lang, Serge (1993), Real and Functional Analysis, Berlin, New York: Springer-Verlag, ISBN 0-387-94001-4
Rudin, Walter (1976), Principles of Mathematical Analysis, New York: McGraw-Hill, ISBN 0-07-054235-X
Tao, Terence (2016). "Infinite sets". Analysis I (Third ed.). Singapore: Springer. pp. 181–210. ISBN 978-981-10-1789-6.

[ZeroN-1] $N$ 과 N*= { $1, 2, 3$ , $...}$ $사이$ 에는 분명한 분사가 있기 때문에 0을 자연수로 간주하든 그렇지 않든 아무런 차이가 없다.어느 경우든, 이 기사는 ISO 31-11과 0을 자연수로 하는 수학 논리학의 표준 규약을 따르고 있습니다.

[24] 증명: f $(m,$ $n)$ = $23$ 에^mⁿ $의해$ $주어진$ 함수 f : $N$ × $N$ → N은 ^[22]주입식이기 때문에 정의의 결과로 $계산$ 될 $수$ $있음$ 을 관찰한다.그런 다음 두 개의 계수 집합의 데카르트 곱은 계수할 수 있다. 왜냐하면 $A$ 와 B가 계수할 수 있는 두 집합이면 $제외$ $f$ : $N$ → $A$ 와g : $N$ → $B$ 가 존재하기 때문이다.그래서...
$f \times g : N \times N \to A \times B$

는 가산 가능한 $집합$ N × $N$ 에서 $집합$ A × $B$ 로의 돌출이며, 결과는 A × $B$ 가 가산 가능한 것을 $의미$ 한다.이 결과는 계산 가능한 집합의 유한 집합의 데카르트 곱으로 일반화되며, 그 증거는 집합의 집합 수에 대한 유도에 따른다.

[25] 증명: $n$ 이 음이 아니면 f( $n$ ) = $2$ 로ⁿ $주어지는$ 함수 $f$ : $Z$ → N, n이 음이면 $f$ $(n)$ = $3$ 으로⁻ⁿ 주어지는 함수 f : Z는 셀 수 있다.g $(m,$ $n)$ = $m /(n +$ 1)에 $의해$ 주어진 $함수$ g : $Z$ × $N$ → $Q$ 는 계수 $집합$ Z × $N$ 에서 $유리$ Q로의 돌출이기 때문에 계수할 수 $있다$ .

[27] 증명: 정의에 따르면, 모든 대수적 수(복소수 포함)는 정수 계수를 갖는 다항식의 근입니다.대수 $({displaystyle \alpha$ 를 지정하면 0 $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ + $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ + $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ + $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ + $({$ )로 $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ . $}x^{1}+a_{2$ $}x^{2}+\cdots$ + $a_{n$ $}$ x $^{$ n $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ }}은 $\alpha$ (는) $정수$ 계수를 갖는 다항식입니다 $.$ $α$ 는 다항식의 k번째 루트이며, 여기서 루트는 작은 것부터 큰 것까지 절대값으로 정렬된 다음 작은 것부터 큰 것까지 인수로 정렬됩니다.f $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $k$ - $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ → $3$ a 0 $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ a $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ 7 $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ p $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ + $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ n $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ { $display f$ ( \ $alpha$ ) = $2$ p k - 1 → 2 $cdot$ 3 $^{a _$ 0 } \ $cdot 5$ ^ { 1 }에 $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ 주어지는 주입(즉, 일대일) 함수 f : $A$ → Q)를 정의할 수 있다.

[30] 증명: A가 I={1, ...,n}의 각 i에 대해 계수 가능한 $집합$ 이라면_i, $각$ n에 대해 $사사함수 i$ $g :$ $N i$ → A가 존재하며, 따라서 함수는 $G:I\times \mathbf {N} \to \bigcup _{i\in I}A_{i$ G $(i,$ $m)$ = $g i (m)$ 로 주어지는 는 굴절이다.I × $N$ 은 계수 $가능$ 하므로 합집합 ${\textstyle \bigcup _{i\in I}A_{i}}$ i ${\textstyle \bigcup _{i\in I}A_{i}}$ I ${\textstyle \bigcup _{i\in I}A_{i}}$ \ $textstyle$ \ $bigcup$ _ ${ i$ \ $in$ I } $A$ _ { $i$ }는 ${\textstyle \bigcup _{i\in I}A_{i}}$ 계수 가능합니다.

[31] 증명: 유한한 경우와 마찬가지로 I=N과 우리는 N의 $각$ $i$ 에 대해 $N$ 에서 $A$ 까지의_i 사출의 빈 집합에서 $사출 i$ g를 선택하기 위해 계산 가능한 선택 공리를 사용한다.

[32] 증명: (1) T가 계수 가능한 경우 주입 함수 h : T → N이 있음을 관찰하고, f : S → T가 주사인 경우 조성물 h o f : S → N이 주사되므로 S는 계수 가능하다.(2) S가 셀 수 있는 경우 S가 비어 있거나 surjective 함수 h : N → S가 있는지 관찰한다.g : S → T이면 S와 T가 모두 비어 있거나 g o h : N → T의 조성이 surjective이다.어느 경우든 T는 셀 수 있다.

[33] 토폴로지 증명은 Cantor의 첫 번째 불가산성 증명과 유한 교차로 속성#응용 프로그램을 참조하십시오.

[2] Manetti, Marco (19 June 2015). Topology. Springer. p. 26. ISBN 978-3-319-16958-3.

[Rudin-3] 루딘 1976, 제2장

[4] 타오 2016, 181페이지

[5] 캄케 1950, 2페이지

[Lang-6] 제1장 제2장 Lang 1993

[Apostol-7] 아포톨 1969, 23페이지, 1.14장

[8] Thierry, Vialar (4 April 2017). Handbook of Mathematics. BoD - Books on Demand. p. 24. ISBN 978-2-9551990-1-5.

[9] Mukherjee, Subir Kumar (2009). First Course in Real Analysis. Academic Publishers. p. 22. ISBN 978-81-89781-90-3.

[10] Yaqub, Aladdin M. (24 October 2014). An Introduction to Metalogic. Broadview Press. ISBN 978-1-4604-0244-3.

[Singh-11] Singh, Tej Bahadur (17 May 2019). Introduction to Topology. Springer. p. 422. ISBN 978-981-13-6954-4.

[Katzourakis-12] Katzourakis, Nikolaos; Varvaruca, Eugen (2 January 2018). An Illustrative Introduction to Modern Analysis. CRC Press. ISBN 978-1-351-76532-9.

[13] Halmos 1960, 페이지 91

[14] Weisstein, Eric W. "Countable Set". mathworld.wolfram.com. Retrieved 2020-09-06.

[15] 캄케 1950, 2페이지

[16] Dlab, Vlastimil; Williams, Kenneth S. (9 June 2020). Invitation To Algebra: A Resource Compendium For Teachers, Advanced Undergraduate Students And Graduate Students In Mathematics. World Scientific. p. 8. ISBN 978-981-12-1999-3.

[17] 타오 2016, 182페이지

[18] Stillwell, John C. (2010), Roads to Infinity: The Mathematics of Truth and Proof, CRC Press, p. 10, ISBN 9781439865507, Cantor's discovery of uncountable sets in 1874 was one of the most unexpected events in the history of mathematics. Before 1874, infinity was not even considered a legitimate mathematical subject by most people, so the need to distinguish between countable and uncountable infinities could not have been imagined.

[19] 칸토르 1878 페이지 242

[20] Ferreiros 2007, 268페이지, 272-273.

[21] "What Are Sets and Roster Form?". expii. 2021-05-09. Archived from the original on 2020-09-18.

[22] Halmos 1960, 페이지 92

[23] 아벨스고르 1990, 182페이지

[26] 캄케 1950, 3~4페이지

[28] Avelsgaard 1990, 페이지 180

[29] Fletcher & Patty 1988, 187페이지

[a]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[b]

[c]

[23]

[d]

[24]

[25]

[e]

[f]

[g]

[h]

[22]

v t 번호 체계
카운트 가능 세트	자연수( $\mathbb {N}$ \ $displaystyle \mathbb {N$ ) $\mathbb {Z}$ ( $\mathbb {Z}$ Z \ $displaystyle \mathbb {Z$ ) 유리수( $\$ 구성 가능한 수 $\mathbb {A}$ 숫자( A $\$ ) 기간 계산 가능한 수 산술적 수 이론적으로 정의할 수 있는 수 가우스 정수
합성 대수	나눗셈 대수:실수( $\$ 복소수( $\mathbb {C}$ $\$ ) 4분위 ( $\mathbb {H}$ $\$ ) 옥토니언( $\$
분열되다 종류들	$(\$ 이상 $):$ 분할복소수 스플릿 쿼터 분할 옥토네이션 $(\$ 이상 $):$ 바이콤플렉스 번호 비쿼터니온 바이오크토니온
기타 하이퍼컴플렉스	이중 번호 이중 사분위수 이중 복소수 쌍곡선 사분위수 Sedenions ( $\mathbb {S}$ { \ $displaystyle$ \ $mathbb$ { S $}$ ) 스플릿 바이쿼터니온 멀티플렉스 번호 기하학 대수 물리 공간의 대수 시공간 대수
기타 타입	기수 확장 자연수 무리수 퍼지 수 초실수 리바이 시비타 필드 초현실적 수 초월수 서수 p-adic 번호(p-adic 솔레노이드) 초자연수 초실수
분류 목록.

v t 집합론
개요	집합(수학)
악리	부가 선택. 셀 수 있다 의존하는 세계적인 시공성(V=L) 결정성 확장 기능 Infinity 크기 제한 페어링 전원 세트 규칙성 유니언 마틴의 공리 Axiom 스키마 치환 사양
운용	데카르트 곱 보완(설정 차이) 드 모르간의 법칙 분리 결합 교차로 전원 세트 대칭차 유니언
개념 방법들	카디널리티 기수(대) 학급 구성 가능한 우주 연속체 가설 대각 인수 요소 순서쌍 태플 가족 강제 일대일 대응 서수 Set-Builder 표기법 초한 유도 벤도
유형 설정	비정질 카운트 가능 빈 유한(전통적으로) 흐릿하다 무한(데데킨드 무한) 재귀적 싱글턴 서브셋 · 슈퍼셋 추이적 셀 수 없다 유니버설
이론들	대안 자명한 천진난만 칸토르의 정리 체르멜로 일반 프린키피아 매스매티카 새로운 기초 체르멜로프랭켈 폰 노이만-베네이스괴델 모스켈리 크립케-플라텍 타르스키 그로텐디크
패러독스 문제	러셀의 역설 서슬린 문제 부랄리-포르티 역설
집합 이론가	아브라함 프렝켈 버트런드 러셀 에른스트 체르멜로 게오르크 칸토르 요한 폰 노이만 쿠르트 괴델 폴 버네이즈 폴 코헨 리하르트 데데킨트 토머스 젝 토랄프 스콜렘 윌러드 콰인

Search

카운트 가능 집합

네임스페이스

더

목차

용어에 관한 주의사항

정의.

역사

서론

정식 개요

집합론의 최소 모델은 셀 수 있다.

총주문수

「」를 참조해 주세요.

메모들

인용문

레퍼런스

Search

카운트 가능 집합

용어에 관한 주의사항

정의.

역사

서론

정식 개요

집합론의 최소 모델은 셀 수 있다.

총주문수

「 」를 참조해 주세요.

메모들

인용문

레퍼런스

「」를 참조해 주세요.