구부러진 기능
Bent function
조합론의 수학적 분야에서 구부러진 함수는 최대 비선형인 특수한 부울함수입니다. 진실 테이블 사이의 해밍 거리에 의해 측정될 때 가능한 모든 선형 및 아핀 함수의 집합과는 다릅니다.구체적으로는 함수의 출력과 선형함수의 최대 상관관계가 최소임을 의미한다.또한 벤트 함수의 도함수는 균형 잡힌 부울 함수이므로 입력 변수가 변경될 경우 출력 값이 변경될 확률이 50%입니다.
최대 비선형성은 아핀(선형) 함수에 의해 구부러진 함수를 근사하는 것은 어려운 것으로 선형 암호해석에 대한 방어에 유용한 특성이다.또, 함수의 출력의 변화를 검출하면, 입력에 어떠한 변화가 일어났는지에 관한 정보가 생성되지 않기 때문에, 차분 암호 해석에 대한 영향을 받지 않게 된다.
구부러진 함수는 [1]1976년까지 발표되지 않은 연구에서 1960년대에 오스카 로타우스에 의해 정의되고 명명되었다.암호학에서의 응용을 위해 광범위하게 연구되어 왔지만 스펙트럼 확산, 부호화 이론 및 조합 설계에도 적용되었다.정의는 여러 가지 방법으로 확장될 수 있으며, 이는 원본의 많은 유용한 속성을 공유하는 여러 클래스의 일반화된 구부러짐 함수로 이어질 수 있습니다.
1962년 [2]구소련에서 V. A. 엘리세프와 O. P. 스테픈코프는 최소 기능이라고 불리는 구부러진 기능을 연구한 것으로 알려져 있다.그러나 그들의 결과는 아직 기밀 해제되지 않았다.
구부러진 함수는 완전 비선형(PN) 부울 함수라고도 합니다.가능한 한 완전한 비선형성에 가까운 특정 함수(예: 홀수 비트 수 또는 벡터 함수)는 거의 완벽한 비선형(APN)[3]으로 알려져 있다.
월시 변환
굽힘 함수는 Walsh 변환의 관점에서 정의됩니다.f : n 2 {\ f \의 월시 변환은 f : { : \}\ {z입니다.
여기서 a · x = ax11 + ax22 + … + axnn (mod 2)는 [4]Z 단위의n
2 도트 곱이다.또는 S(a) = { x zn
2 Z : f(x) = a · x } 및 S1(a) = { x zn
2 Z : f(x) a a · x } 로 한다0.그러면0 S(a1) + S(a) = 2이므로n
부울 함수 f 및 µn
2 Z에 대해 변환은 범위 내에 있습니다.
또한 선형 함수0 f(x) = a · x 및 아핀 함수1 f(x) = a · x + 1은 두 극단적인 경우에 해당한다.
따라서 각 a µn
2 Z에 f () \ ( }의 값은 함수 f(x)가01 f(x) ~ f(x)의 범위에 있는 것을 나타냅니다.
정의 및 속성
Rothaus는 굽힘 함수를 부울 f : 2 {\ f로 정의했으며, 이 함수는 월시 변환의 절대값이 일정합니다.구부러진 함수는 어떤 의미에서 모든 아핀 함수와 등거리이므로 어떤 아핀 함수와도 동일하게 근사하기 어렵습니다.
구부러진 함수의 가장 간단한 예는 대수 정규 형식으로 쓰여진 F(x1, x2) = xx12 및 G(x1, x2, x34, x12) = xx34 f xx이다.이 패턴은 계속됩니다12.xx34 ⊕ xx ⊕ … xxn−1n xx \ \ {\ \ { Z } {} 。단, n이 [5]증가할 때마다 그 외의 다양한 굽힘 가 존재합니다.x µ Z가n
2 사전순으로 취해진 값(-1)f(x)의 시퀀스를 벤드 시퀀스라고 합니다.벤트 함수와 벤드 시퀀스는 동등한 속성을 가집니다.이 ±1 형태에서 월시 변환은 다음과 같이 쉽게 계산된다.
여기서 W(2n)는 자연순서 Walsh 행렬이며, 시퀀스는 [6]열 벡터로 처리된다.
Rothaus는 구부러진 함수는 짝수 n에 대해서만 존재하며 구부러진 함수 f,^ (a ) n 2 \ \left (= 2 {n}} } } for an
2 z [4]Z에 대해서만 존재한다는 것을 증명했다. f 스타일 는 g도 구부러진다. 경우 g (a ) 2 (-)f ( (a) = { (-는 f와 g는 이중 [6]함수로 간주됩니다.
모든 구부러진 기능 2n−1±2.mw-parser-output .frac{white-space:nowrap}.mw-parser-output.frac.num,.mw-parser-output.frac .den{:80%;line-height:0;vertical-align:슈퍼 font-size}.mw-parser-output.frac .den{vertical-align:서브}.mw-parser-output .sr-only{의Hamming 무게(횟수 가치 1이 걸린다) 가지고 있다.국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}n⁄2−1고, 사실 한점을 두 번호 중에서 아핀 기능에 동의한다.따라서 f의 비선형성(최소 횟수는 아핀 함수와 동일)은n−1 2 - 2로n⁄2−1, 가능한 최대값입니다.반대로 비선형성이n−1 2 - 2인n⁄2−1 부울 함수는 [4]구부러집니다.대수 정규 형식에서 f의 정도(f의 비선형 순서라고 함)는 최대 n most2이다(n > [5]2의 경우).
여러 변수의 부울 함수 중에서 벤트 함수는 매우 드물지만, 여러 가지 종류가 있습니다.균질함수나[7] 유한장상의 [8]단항식으로부터 발생하는 것과 같은 특수한 종류의 굽힘함수에 대한 상세한 연구가 있었지만, 지금까지 굽힘함수는 완전한 열거 또는 분류에 대한 모든 시도를 무시해 왔다.
구성
구부러진 [2]기능에는 몇 가지 유형의 구조가 있습니다.
- 조합 구조: 반복 시공, Maiorana-McFarland 시공, 부분 확산, Dillon's and Dobbertin의 구부러진 함수, 최소 굽힘 함수, 구부러진 반복 함수
- 대수적 구조: 골드, 딜론, 카사미, 칸토-리안더 및 칸토-샤르핀-쿠이레얀 지수를 갖는 단항 굽힘 함수, 니호 굽힘 함수 등
적용들
1982년 초에는 구부러진 함수에 기초한 최대 길이 시퀀스가 [9]CDMA에서 사용하기 위한 골드 코드 및 카사미 코드와 유사한 상호 상관 및 자기 상관 특성을 갖는 것으로 밝혀졌다.이러한 시퀀스는 스펙트럼 확산 기법에 여러 가지 응용 분야를 가지고 있다.
구부러진 함수의 특성은 입력과 출력 사이의 관계를 모호하게 하려는 현대 디지털 암호학에서 당연히 관심을 끈다.1988년까지 Forré는 함수의 월시 변환이 엄밀한 눈사태 기준(SAC)과 고차 일반화를 충족한다는 것을 보여주기 위해 사용될 수 있다는 것을 인식하고, 이 도구를 거의 완벽한 [10]확산을 달성하는 좋은 S-박스에 대한 후보를 선택하기 위해 추천했다.실제로 SAC를 가능한 한 높은 차수로 만족시키는 기능은 항상 [11]구부러져 있다.또한 구부러진 함수는 f(x+a)+f(x)가 상수인 비제로 벡터 a라고 불리는 선형 구조를 갖는 것으로부터 가능한 한 멀리 떨어져 있다.미분 암호 분석의 언어(이 특성이 발견된 후 도입됨)에서, 0이 아닌 모든 점 a(즉a, f(x) = f(x + a) + f(x))에서 구부러진 함수 f의 도함수는 각 값의 정확히 절반을 차지하는 균형 부울 함수이다.이 성질을 [5]완전 비선형성이라고 합니다.
그러한 양호한 확산 특성, 분명히 미분 암호 해석에 대한 완벽한 저항성 및 선형 암호 해석에 대한 정의를 고려할 때, 처음에는 S-box와 같은 안전한 암호 기능을 위해 구부러진 함수가 이상적인 선택으로 보일 수 있다.그들의 치명적인 단점은 균형을 잡지 못한다는 것이다.특히 구부러진 함수에서 직접 반전 S박스를 구축할 수 없고 구부러진 결합 함수를 이용한 스트림 암호는 상관 공격에 취약하다.대신 구부러진 함수로 시작하여 결과가 균형을 이룰 때까지 무작위로 적절한 값을 보완할 수 있습니다.수정된 함수는 여전히 높은 비선형성을 가지고 있으며, 이러한 함수는 매우 드물기 때문에 프로세스는 brute-force [5]검색보다 훨씬 더 빠릅니다.단, 이 방법으로 생성되는 기능은 SAC를 만족시키지 못해도 다른 바람직한 특성을 잃을 수 있습니다.따라서 신중한 테스트가 필요합니다.[11]많은 암호학자들이 구부러진 함수의 좋은 암호화 품질을 가능한 [12][13][14]한 많이 보존하는 균형 잡힌 함수를 생성하는 기술을 연구해 왔습니다.
이 이론적 연구 중 일부는 실제 암호 알고리즘에 통합되었습니다.Carlisle Adams와 Stafford Tavares가 블록 암호 CAST-128과 CAST-256을 위한 S-박스를 구성하기 위해 사용한 CAST 설계 절차는 구부러진 [14]기능을 이용한다.암호화 해시함수 HAVAL은 6개의 [15]변수에서 구부러진 함수의 등가 클래스 4개 모두를 대표하는 부울함수를 사용합니다.스트림 암호 그레인에서는 비선형 피드백 다항식이 벤트 함수와 선형 [16]함수의 합인 NLFSR을 사용합니다.
일반화
Tokareva의 2015년 [2]논문에는 구부러진 기능의 일반화가 25개 이상 기술되어 있다.대수적 일반화(q값의 굽힘 함수, p-ary 굽힘 함수, 유한 필드의 굽힘 함수, 슈미트의 일반화 부울 굽힘 함수, 단위 원의 유한 아벨 군에서 복소수 집합으로 굽힘 함수, 유한 아벨 군에서 유한 아벨 군으로 굽힘 함수, 비-아벨리언 벤)가 있다.t 함수, 벡터 G-벤트 함수, 유한 아벨 군에서의 다차원 벤트 함수, 조합 일반화(대칭 벤트 함수, 균질 벤트 함수, 회전 대칭 벤트 함수, 정규 벤트 함수, 자기 이중 및 반 자기 이중 벤트 함수, 부분적으로 정의된 벤트 함수, 평탄화 함수, Z-벤트 함수함수와 양자 굽힘 함수) 및 암호 일반화(굴곡 함수, 균형 굽힘 함수, 부분 굽힘 함수, 하이퍼 굽힘 함수, 고차 굽힘 함수, k 굽힘 함수)입니다.
일반화된 굽힘 함수의 가장 일반적인 클래스는 mod m 유형입니다 : m { \ f : \ {{ \ \ {} 。이러한 클래스는 다음과 같습니다.
는 일정한 절대값n/2 m을 가집니다.완전 비선형 f : m \ f : \ { _ { m 、 0이 아닌 모든 a, f(x + a) - f(a)에n − 1 대해 m회마다 취하는 것을 일반화 굽힘함수이다.m이 소수이면 그 반대가 참이다.대부분의 경우 소수 m만 고려된다.홀수 소수 m의 경우, 모든 양의 n, 짝수 및 홀수에 대해 일반화 굽힘 함수가 있습니다.이들은 바이너리 벤트 [17][18]함수와 동일한 우수한 암호화 특성을 가지고 있습니다.
반굽힘 함수는 굽힘 함수의 홀수 차수입니다.반벤트 함수는 f: m m {\ f ~ \이며, n은 홀수이므로 {는 0 및(n+1)/2 m 값만 취한다또한 암호화 특성이 우수하며, 그 중 일부는 가능한 모든 값을 동일한 빈도로 [19]균등하게 채택하여 균형을 이루고 있습니다.
부분적으로 구부러진 함수는 월시 변환 및 자기 상관 함수의 조건에 의해 정의된 큰 클래스를 형성합니다.모든 아핀 및 구부러진 기능은 부분적으로 구부러져 있습니다.이것은 차례로 고원 [20]함수의 적절한 하위 클래스입니다.
하이퍼벤트 함수 뒤에 있는 아이디어는 아핀 함수뿐만 아니라 유한 필드 GF(2) 상의n 비주사적 모노물질로부터 오는 모든 부울 함수에 대한 최소 거리를 최대화하는 것입니다.이러한 함수의 경우 이 거리는 일정하므로 보간 공격에 저항할 수 있습니다.
암호학적으로 중요한 클래스f : n \ f \ _ \to \mathbbb {Z} _{2}^{n \to \mathbbb {Z}에 거의 구부러진 함수 및 비뚤어진 함수 등의 다른 관련 이름이 붙여졌다.구부러진 함수 자체는 아니지만(부울 함수도 아님), 구부러진 함수와 밀접하게 관련되어 있어 비선형성이 우수합니다.
「 」를 참조해 주세요.
레퍼런스
- ^ O. S. Rothaus (May 1976). "On "Bent" Functions". Journal of Combinatorial Theory, Series A. 20 (3): 300–305. doi:10.1016/0097-3165(76)90024-8. ISSN 0097-3165.
- ^ a b c N. Tokareva (2015). Bent functions: results and applications to cryptography. Academic Press. ISBN 9780128023181.
- ^ Blondeau; Nyberg (2015-03-01). "Perfect nonlinear functions and cryptography". Finite Fields and Their Applications. 32: 120–147. doi:10.1016/j.ffa.2014.10.007. ISSN 1071-5797.
- ^ a b c C. Qu; J. Seberry; T. Xia (29 December 2001). "Boolean Functions in Cryptography". Retrieved 14 September 2009.
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - ^ a b c d W. Meier; O. Staffelbach (April 1989). Nonlinearity Criteria for Cryptographic Functions. Eurocrypt '89. pp. 549–562.
- ^ a b C. Carlet; L.E. Danielsen; M.G. Parker; P. Solé (19 May 2008). Self Dual Bent Functions (PDF). Fourth International Workshop on Boolean Functions: Cryptography and Applications (BFCA '08). Retrieved 21 September 2009.
- ^ T. Xia; J. Seberry; J. Pieprzyk; C. Charnes (June 2004). "Homogeneous bent functions of degree n in 2n variables do not exist for n > 3". Discrete Applied Mathematics. 142 (1–3): 127–132. doi:10.1016/j.dam.2004.02.006. ISSN 0166-218X. Retrieved 21 September 2009.
- ^ A. Canteaut; P. Charpin; G. Kyureghyan (January 2008). "A new class of monomial bent functions" (PDF). Finite Fields and Their Applications. 14 (1): 221–241. doi:10.1016/j.ffa.2007.02.004. ISSN 1071-5797. Archived from the original (PDF) on 21 July 2011. Retrieved 21 September 2009.
- ^ J. Olsen; R. Scholtz; L. Welch (November 1982). "Bent-Function Sequences". IEEE Transactions on Information Theory. IT-28 (6): 858–864. doi:10.1109/tit.1982.1056589. ISSN 0018-9448. Archived from the original on 22 July 2011. Retrieved 24 September 2009.
- ^ R. Forré (August 1988). The Strict Avalanche Criterion: Spectral Properties of Boolean Functions and an Extended Definition. CRYPTO '88. pp. 450–468.
- ^ a b C. Adams; S. Tavares (January 1990). "The Use of Bent Sequences to Achieve Higher-Order Strict Avalanche Criterion in S-box Design". Technical Report TR 90-013. Queen's University. CiteSeerX 10.1.1.41.8374.
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - ^ K. Nyberg (April 1991). Perfect nonlinear S-boxes. Eurocrypt '91. pp. 378–386.
- ^ J. Seberry; X. Zhang (December 1992). Highly Nonlinear 0–1 Balanced Boolean Functions Satisfying Strict Avalanche Criterion. AUSCRYPT '92. pp. 143–155. CiteSeerX 10.1.1.57.4992.
- ^ a b C. Adams (November 1997). "Constructing Symmetric Ciphers Using the CAST Design Procedure". Designs, Codes and Cryptography. 12 (3): 283–316. doi:10.1023/A:1008229029587. ISSN 0925-1022. S2CID 14365543. Archived from the original on 26 October 2008. Retrieved 20 September 2009.
- ^ Y. Zheng; J. Pieprzyk; J. Seberry (December 1992). HAVAL – a one-way hashing algorithm with variable length of output. AUSCRYPT '92. pp. 83–104. Retrieved 20 June 2015.
- ^ M. Hell; T. Johansson; A. Maximov; W. Meier. "A Stream Cipher Proposal: Grain-128" (PDF). Retrieved 24 September 2009.
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - ^ K. Nyberg (May 1990). Constructions of bent functions and difference sets. Eurocrypt '90. pp. 151–160.
- ^ Shashi Kant Pandey; B.K. Dass (September 2017). "On Walsh Spectrum of Cryptographic Boolean Function". Defence Science Journal. 67 (5): 536–541. doi:10.14429/dsj.67.10638. ISSN 0011-748X.
- ^ K. Khoo; G. Gong; D. Stinson (February 2006). "A new characterization of semi-bent and bent functions on finite fields" (PostScript). Designs, Codes and Cryptography. 38 (2): 279–295. CiteSeerX 10.1.1.10.6303. doi:10.1007/s10623-005-6345-x. ISSN 0925-1022. S2CID 10572850. Retrieved 24 September 2009.
- ^ Y. Zheng; X. Zhang (November 1999). Plateaued Functions. Second International Conference on Information and Communication Security (ICICS '99). pp. 284–300. Retrieved 24 September 2009.
추가 정보
- C. Carlet (May 1993). Two New Classes of Bent Functions. Eurocrypt '93. pp. 77–101.
- J. Seberry; X. Zhang (March 1994). "Constructions of Bent Functions from Two Known Bent Functions". Australasian Journal of Combinatorics. 9: 21–35. CiteSeerX 10.1.1.55.531. ISSN 1034-4942.
- T. Neumann (May 2006). "Bent Functions". CiteSeerX 10.1.1.85.8731.
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - Colbourn, Charles J.; Dinitz, Jeffrey H. (2006). Handbook of Combinatorial Designs (2nd ed.). CRC Press. pp. 337–339. ISBN 978-1-58488-506-1.
- Cusick, T.W.; Stanica, P. (2009). Cryptographic Boolean Functions and Applications. Academic Press. ISBN 9780123748904.

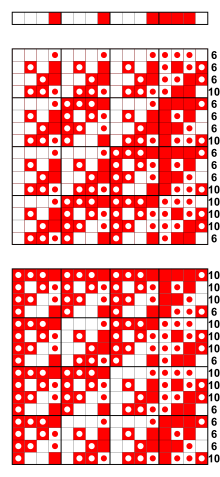
 구부러져 있습니다.즉, 그 비선형성은 6입니다(이러한 월시 매트릭스가 나타내고 있습니다).다음 공식은 4-아리 함수의 비선형성이 6일 때 구부러진다는 것을 보여 줍니다.
구부러져 있습니다.즉, 그 비선형성은 6입니다(이러한 월시 매트릭스가 나타내고 있습니다).다음 공식은 4-아리 함수의 비선형성이 6일 때 구부러진다는 것을 보여 줍니다.
 월시 변환은
월시 변환은 











 0 및(n+1)/2 m 값만 취한다
0 및(n+1)/2 m 값만 취한다


