자연적으로 순서가 정해진 하다마드 행렬은 순서가 정해진 하다마드 행렬로 퍼졌다. 자연적으로 순서가 정해진 행렬에서 행당 부호 변화 수는 (0, 15, 7, 8, 3, 12, 4, 11, 1, 1, 14, 6, 9, 2, 13, 5, 10)이며, 순차 순서가 정해진 행렬에서는 부호 변화 수가 연속적이다. 
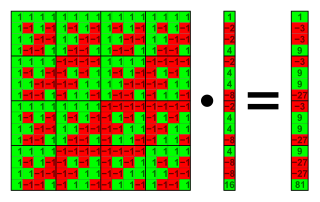
매트릭스 제품으로서의 바이너리 월시 매트릭스. 이진 행렬(흰색 0, 빨간색 1)은 F의2 연산 결과물이다. 회색 번호는 R의 연산 결과를 나타낸다. 
월시 매트릭스는 손상된 TIFF(Tag Image File Format) 사진에 나타난다. 수학에서 월시 행렬은 차원 2의n 특정한 제곱 행렬이며, 여기서 n은 어떤 특정한 자연수다. 행렬의 항목은 +1 또는 -1이며 행과 열은 직교, 즉 도트 곱은 0이다. 월시 매트릭스는 1923년 조셉 월시에 의해 제안되었다.[1] 월시 행렬의 각 행은 월시 함수에 해당한다.
월시 행렬은 하다마르 행렬의 특별한 경우다. 자연적으로 순서가 정해진 하다마드 행렬은 아래의 재귀 공식에 의해 정의되며, 연속 순서가 정해진 하다마드 행렬은 행을 재정렬하여 행의 변화 횟수가 증가하도록 형성된다.[1] 헷갈리게, 서로 다른 출처는 두 행렬을 월시 행렬이라고 부른다.
월시 매트릭스(및 월시 함수)는 월시 변환을 계산하는 데 사용되며 특정 신호 처리 작업의 효율적인 구현에 응용 프로그램이 있다.
공식
k ∈ N에 대한 치수 2의k Hadamard 행렬은 재귀 공식에 의해 주어진다(Hadamard 행렬의 최저 순서는 2).

그리고 일반적으로

2 ≤ k ∈ N에 대하여, 여기서 ⊗은 Kronecker 제품을 나타낸다.
순열
각 행의 기호 변경 수에 따라 행렬의 행을 재정렬하십시오. 예를 들면,

연속된 행은 0, 3, 1, 2 부호가 바뀐다. 시퀀스 순서로 행을 재정렬하는 경우:

그러면 연속된 행은 0, 1, 2, 3개의 부호가 바뀐다.
월시 행렬의 대체 형태
시퀀스 오더
월시 행렬의 행 순서 순서는 먼저 비트 역순열을 적용한 다음 그레이 코드 순열을 적용하여 Hadamard 행렬의 순서에서 도출할 수 있다.[2]

여기서 연속된 행에 0, 1, 2, 3, 4, 5, 6 및 7 기호가 변경된다.
디아디치 오더

여기서 연속된 행에 0, 1, 3, 2, 7, 6, 4, 5 기호가 변경된다.
자연순서

여기서 연속된 행에 0, 7, 3, 4, 1, 6, 2, 5 기호가 변경된다.
참고 항목
 | 위키미디어 커먼즈에는 월시 매트릭스와 관련된 미디어가 있다. |
참조