블린-퐁 반사 모델

변형 퐁 반사모델이라고도 불리는 블린-퐁 반사모델은 짐 블린이 퐁 반사모델로 개발한 수정모델이다.^[1]

Blinn-Phong은 OpenGL과 Direct3D의 고정 기능 파이프라인(Direct3D 10 및 OpenGL 3.1 이전)에서 사용되는 기본 음영 모델로, 그래픽 파이프라인을 통과할 때 각 정점에 대해 수행된다. 정점 사이의 픽셀 값은 더 계산적으로 비싼 Phong 음영이 아닌 Guaud 음영에 의해 기본적으로 보간된다.^[2]

설명

Phong 및 Blinn-Phong 음영 계산 벡터

Phong shading에서는 뷰어(V)와 $R\cdot V$ 표면의 광원(L) 반사(R) 빔 사이의 도트 제품 $R\cdot V$ ⋅ $R\cdot V$ $R\cdot V$ 을(를) 계속 재계산해야 한다.

대신 뷰어와 광원 벡터 사이의 중간 벡터를 계산하면

H={\frac {L+V}{\\왼쪽\L+V\오른쪽\}}

$R\cdot V$ $R$ $R\cdot V$ $R\cdot V$ ${\displaystyle R\cdot$ $V$ $}$ 은(는) $N\cdot H$ $N\cdot H$ H ${\$ $displaystyle$ N $\cdot$ H $}($ 으)로 교체할 $R\cdot V$ 수 $있으며$ , 여기서 N {\displaystyle $N}$ 은 $N$ 정규화된 표면이다 $N\cdot H$ 위의 방정식에서 $L$ ${\$ $L}$ 과 $L$ V $V$ 은 모두 정규화된 벡터이며 $V$ , $H$ $H$ 은 $P_{H}$ $V=P_{H}(-L),$ = $V=P_{H}(-L),$ $V=P_{H}(-L),$ ( $V=P_{H}(-L),$ - $V=P_{H}(-L),$ ) $V=P_{H}(-L),$ , ${\displaystyle V=$ $P_$ ${H}(-L)$ 식에 $V=P_{H}(-L),$ $P_{H}$ 해결책이다 $H$ $.$ $H}}$ 은 $P_{H}$ 기원을 포함하는 하이퍼플레인에서 점을 반영하는 하우스홀더 매트릭스로, 정상 $H .$ ${\displaystyle$ H $.}$ 을(를) 가지고 있다.

이 도트 제품은 V, L, N, R이 모두 같은 평면에 놓여 있을 경우 퐁의 도트 제품으로 대표되는 각도의 절반인 각도의 코사인을 나타낸다. 벡터가 같은 평면에 있지 않을 때, 특히 각도가 작을 때 각 사이의 관계는 대략적으로 참으로 유지된다. 따라서 N과 H 사이의 각도를 중간 각도라고 부르기도 한다.

하프 벡터와 표면 정규 사이의 각도가 Phong의 모델에 사용된 R과 V 사이의 각도보다 작을 가능성이 있다는 점을 고려하면(표면이 더 클 것 같은 매우 가파른 각도에서 보는 경우는 제외), Phong이 $\left(R\cdot V\right)^{\alpha },$ $\left(R\cdot V\right)^{\alpha },$ $\left(R\cdot V\right)^{\alpha },$ ) $\left(R\cdot V\right)^{\alpha },$ , $\left (R\cdot V\right)^{\\alpha$ 을 사용하고 있기 때문이다. 지수를 $\alpha ^{\prime }>\alpha$ α > $\alpha ^{\prime }>\alpha$ > α $\alpha ^{\premy }}$ $\left(N\cdot H\right)^{\alpha ^{\prime }}$ $\left(N\cdot H\right)^{\alpha ^{\prime }}$ α α $\left(N\cdot H\right)^{\alpha ^{\prime }}$ ${\$ 에 $\alpha ^{\prime }>\alpha$ $\left(N\cdot H\right)^{\alpha ^{\prime }}$ 가깝게 설정할 수 있다 $\left(N\cdot H\right)^{\alpha ^{\prime }}$

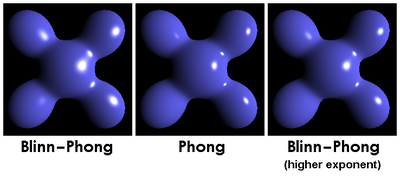
전면 조명 표면(뷰어를 향한 표면의 규격 반사)의 경우 $\alpha ^{\prime }=4\,\alpha$ α $\alpha ^{\prime }=4\,\alpha$ $\alpha ^{\prime }=4\,\alpha$ α = 4 $\alpha ^{\prime }=4\,\alpha$ ${\displaystyle \alpha \alpha ^{\premy$ }=4\,\alpha $}}}$ 는 해당 Phong 반사와 매우 밀접하게 일치하는 규격 하이라이트를 생성한다 $\alpha ^{\prime }=4\,\alpha$ . 그러나 퐁 반사는 평탄한 표면을 위해 항상 둥글지만, 블린-퐁 반사는 표면을 가파른 각도에서 볼 때 타원이 된다. 이는 태양이 수평선에 가까운 바다에 반사되거나, 먼 거리의 불빛이 젖은 포장도로에 반사되는 경우와 비교할 수 있는데, 그 반사광은 항상 수평보다 수직으로 훨씬 더 확장된다.^[3]

또한 Phong 모델에 대한 근사치로 볼 수 있지만, 많은 유형의 표면에서 Phong보다 경험적으로 결정된 양방향 반사율 분포 함수의 보다 정확한 모델을 생산한다.^[4]

효율성

블린퐁은 시청자와 빛이 접근하거나 무한대에 도달하는 등 매우 외진 것으로 취급되는 경우 퐁보다 빠를 것이다. 방향등과 직교/등각 카메라의 경우가 이에 해당한다. 이 경우, 중간 벡터는 단순히 중간 벡터가 시청자의 위치 방향과 빛의 위치 방향에 따라 달라지기 때문에 위치 및 표면 곡률과는 무관하며, 이는 이 먼 거리에서 개별적으로 수렴되므로 중간 벡터는 이 경우에 일정하다고 생각할 수 있다. $따라서$ H $H$ 은 각 조명에 대해 한 번 계산한 다음 전체 프레임에 사용할 수 있으며, 빛과 관점이 동일한 상대적 위치에 있는 동안 실제로 사용할 수 있다. 표면 곡률에 따라 달라지며 이미지의 각 픽셀(또는 꼭지점 조명의 경우 모델의 각 꼭지점)에 대해 다시 계산해야 하는 Phong의 반사 벡터 사용 방법에서는 동일하지 않다. 투시 카메라가 있는 3D 장면에서는 이러한 최적화가 불가능하다.

코드 샘플

하이 레벨 음영 언어 코드 샘플

하이 레벨 셰이딩 언어로 된 이 샘플은 점등에서 확산과 지정광을 결정하는 방법이다. 조명 구조, 표면 공간에서의 위치, 뷰 방향 벡터 및 표면의 정상 등이 통과된다. 조명 구조물이 반환된다.

아래 역시 부정적인 답변의 경우 특정 도트 제품을 0으로 클램프 할 필요가 있다. 그것 없이, 카메라에서 멀어지는 빛은 빛이 그것을 향해 향하는 것과 같은 방식으로 처리된다. 지정학적 계산의 경우, 카메라에서 멀리 떨어진 물체 가장자리에서 반사되는 빛의 부정확한 "할로"가 카메라 쪽으로 반사되는 빛만큼 밝게 나타날 수 있다.

구조상의 조명 {     부유3 확산;     부유3 스펙터클; };  구조상의 포인트라이트 {  부유3 포지션;  부유3 디퓨즈 컬러;  둥둥 뜨다  디퓨즈파워;  부유3 스펙터클 컬러;  둥둥 뜨다  스펙터클파워; };  조명 겟포인트라이트(포인트라이트 빛, 부유3 포스3D, 부유3 뷰디르, 부유3 정상의) {  조명 아웃;  만일 (빛.디퓨즈파워 > 0)  {   부유3 라이트디르 = 빛.포지션 - 포스3D; //3D 표면 공간 위치   둥둥 뜨다 거리를 두다 = 길이(라이트디르);   라이트디르 = 라이트디르 / 거리를 두다; // = 정규화(lightDir);   거리를 두다 = 거리를 두다 * 거리를 두다; //이 선은 역 제곱근을 사용하여 최적화할 수 있다.    // 확산 조명의 강도 0-1 범위 이내로 유지하기 위해 포화상태로 유지한다.   둥둥 뜨다 NdotL = 점을 찍다(정상의, 라이트디르);   둥둥 뜨다 강렬함 = 포화시키다(NdotL);    // 밝은 색상, 전원 및 감쇠로 분산 조명 인수 계산   아웃.확산 = 강렬함 * 빛.디퓨즈 컬러 * 빛.디퓨즈파워 / 거리를 두다;    //광 벡터와 뷰 벡터 사이의 하프 벡터를 계산한다.   //이는 일반적으로 실제 반사 벡터를 계산하는 것보다 느리다.   // 정규화 함수의 역 제곱근으로 인해   부유3 H = 정상화하다(라이트디르 + 뷰디르);    //정형광의 강도   둥둥 뜨다 NdotH = 점을 찍다(정상의, H);   강렬함 = 포우(포화시키다(NdotH), specularHardness);    //정형광 인수 요인을 요약하십시오.   아웃.스펙터클 = 강렬함 * 빛.스펙터클 컬러 * 빛.스펙터클파워 / 거리를 두다;   }  돌아오다 아웃; }

OpenGL Shading 언어 코드 샘플

OpenGL Shading Language의 이 샘플은 두 개의 코드 파일 또는 셰이더로 구성되어 있다. 첫 번째는 소위 정점 쉐이더로 정점 사이에 정상적인 표면을 보간하는 데 사용되는 퐁 음영을 구현한다. 두 번째 셰이더는 소위 파편 쉐이더로 포인트 광원에서 발생하는 확산과 정광 빛을 결정하기 위해 블린-퐁 음영 모델을 구현한다.

정점 셰이더

이 정점 쉐이더는 Phong 음영을 구현한다.

기여하다 vec3 입력위치; 기여하다 vec2 inputTexCoord; 기여하다 vec3 입력 정규 분포;  획일적인 mat4 투영, 모델뷰, 노멀매트;  다변수의 vec3 normalInterp; 다변수의 vec3 vertPos;  공허하게 하다 본래의() {     gl_위치 = 투영 * 모델뷰 * vec4(입력위치, 1.0);     vec4 vertPos4 = 모델뷰 * vec4(입력위치, 1.0);     vertPos = vec3(vertPos4) / vertPos4.w;     normalInterp = vec3(노멀매트 * vec4(입력 정규 분포, 0.0)); }

파편 셰이더

이 조각 셰이더는 블린-퐁 음영 모델^[5] 및 감마 보정을 구현한다.

정밀한 중용의 둥둥 뜨다;  에 vec3 normalInterp; 에 vec3 vertPos;  획일적인 인트로 모드;  경시하다 vec3 라이트포스 = vec3(1.0, 1.0, 1.0); 경시하다 vec3 연한 컬러 = vec3(1.0, 1.0, 1.0); 경시하다 둥둥 뜨다 라이트파워 = 40.0; 경시하다 vec3 앰비언트 컬러 = vec3(0.1, 0.0, 0.0); 경시하다 vec3 디퓨즈 컬러 = vec3(0.5, 0.0, 0.0); 경시하다 vec3 스펙컬러 = vec3(1.0, 1.0, 1.0); 경시하다 둥둥 뜨다 반짝임 = 16.0; 경시하다 둥둥 뜨다 스크린감마 = 2.2; // 모니터가 sRGB 색 공간에 맞게 보정되었다고 가정해 보십시오.  공허하게 하다 본래의() {    vec3 정상의 = 정상화하다(normalInterp);   vec3 라이트디르 = 라이트포스 - vertPos;   둥둥 뜨다 거리를 두다 = 길이(라이트디르);   거리를 두다 = 거리를 두다 * 거리를 두다;   라이트디르 = 정상화하다(라이트디르);    둥둥 뜨다 램버트의 = 맥스.(점을 찍다(라이트디르, 정상의), 0.0);   둥둥 뜨다 정형의 = 0.0;    만일 (램버트의 > 0.0) {      vec3 뷰디르 = 정상화하다(-vertPos);      // 이것은 블린퐁이다.     vec3 하프디르 = 정상화하다(라이트디르 + 뷰디르);     둥둥 뜨다 스펙글 = 맥스.(점을 찍다(하프디르, 정상의), 0.0);     정형의 = 포우(스펙글, 반짝임);             // 이것은 phong (비교용)     만일 (모드 == 2) {       vec3 반사디르 = 반영하다(-라이트디르, 정상의);       스펙글 = 맥스.(점을 찍다(반사디르, 뷰디르), 0.0);       // 여기서 지수가 다르다는 점에 유의       정형의 = 포우(스펙글, 반짝임/4.0);     }   }   vec3 색상선형 = 앰비언트 컬러 +                      디퓨즈 컬러 * 램버트의 * 연한 컬러 * 라이트파워 / 거리를 두다 +                      스펙컬러 * 정형의 * 연한 컬러 * 라이트파워 / 거리를 두다;   // 감마 보정 적용(앰비언트컬러, 디퓨즈컬러 및 스펙컬러로 가정)   // 선형화됨, 즉 감마 보정이 없음)   vec3 colorGamma수정됨 = 포우(색상선형, vec3(1.0 / 스크린감마));   // 조각에 감마 보정 색 사용   gl_Frag Color = vec4(colorGamma수정됨, 1.0); }

컬러스 앰비언트 컬러, 디퓨전 컬러 및 스펙 컬러는 감마 보정되지 않아야 한다. 그것들이 감마 보정 이미지 파일(JPEG, PNG 등)에서 얻은 색이라면, 그것들과 함께 작업하기 전에 선형화되어야 하며, 이것은 채널 값을 $[0, 1]$ 범위로 스케일링하여 영상의 감마값으로 올리는 것으로서, sRGB 색 공간의 영상에 대해서는 (이 특정의 경우에도) 약 2.2로 가정할 수 있다. 색상 공간, 단순한 검정력 관계는 실제 변환의 근사치에 불과하다. 현대의 그래픽 API는 텍스처나 글쓰기에서 프레임 버퍼로 표본을 추출할 때 이 감마 보정을 자동으로 수행할 수 있는 기능을 가지고 있다.^[6]

참고 항목

참조

^ James F. Blinn (1977). "Models of light reflection for computer synthesized pictures". Proc. 4th Annual Conference on Computer Graphics and Interactive Techniques: 192–198. CiteSeerX 10.1.1.131.7741. doi:10.1145/563858.563893. S2CID 8043767.
^ Shreiner, Dave; The Khronos OpenGL ARB Working Group (2010). "The Mathematics of Lighting". OpenGL programming guide : the official guide to learning OpenGL, version 3.0 and 3.1 (7th ed.). Pearson Education, Inc. pp. 240–245. ISBN 978-0-321-55262-4.
^ Krus, Kristofer (2014), Wave Model and Watercraft Model for Simulation of Sea State, Linköping University, p. 97
^ Ngan, Addy; Durand, Frédo; Matusik, Wojciech (2004). "Experimental validation of analytical BRDF models". ACM SIGGRAPH 2004 Sketches on - SIGGRAPH '04. ACM Press: 90. doi:10.1145/1186223.1186336. ISBN 1-59593-836-2. S2CID 9259363. Retrieved 23 April 2019.
^ "WebGL Example: Phong / Blinn Phong Shading". www.mathematik.uni-marburg.de. Retrieved 2019-09-13.
^ https://www.khronos.org/registry/OpenGL/extensions/EXT/EXT_framebuffer_sRGB.txt

[1] James F. Blinn (1977). "Models of light reflection for computer synthesized pictures". Proc. 4th Annual Conference on Computer Graphics and Interactive Techniques: 192–198. CiteSeerX 10.1.1.131.7741. doi:10.1145/563858.563893. S2CID 8043767.

[2] Shreiner, Dave; The Khronos OpenGL ARB Working Group (2010). "The Mathematics of Lighting". OpenGL programming guide : the official guide to learning OpenGL, version 3.0 and 3.1 (7th ed.). Pearson Education, Inc. pp. 240–245. ISBN 978-0-321-55262-4.

[3] Krus, Kristofer (2014), Wave Model and Watercraft Model for Simulation of Sea State, Linköping University, p. 97

[4] Ngan, Addy; Durand, Frédo; Matusik, Wojciech (2004). "Experimental validation of analytical BRDF models". ACM SIGGRAPH 2004 Sketches on - SIGGRAPH '04. ACM Press: 90. doi:10.1145/1186223.1186336. ISBN 1-59593-836-2. S2CID 9259363. Retrieved 23 April 2019.

[5] "WebGL Example: Phong / Blinn Phong Shading". www.mathematik.uni-marburg.de. Retrieved 2019-09-13.

[6] ttps://www.khronos.org/registry/OpenGL/extensions/EXT/EXT_framebuffer_sRGB.txt

[1]

[2]

[3]

[4]

[5]

[6]

Search