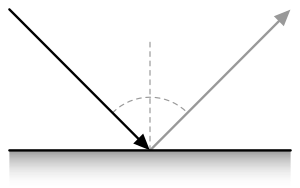
양방향 반사율 분포 함수

BRDF를 정의하는 데 사용되는 벡터를 나타내는 다이어그램입니다. 모든 벡터는 단위 길이입니다.

§

i(\displaystyle

\

mega_{\text{i

}})는 광원을 가리킵니다.

§

r

\

displaystyle

\ obega _ { \

text

{

\omega _{\text{r}}

r } }는

\omega _{\text{r}}

뷰어(카메라)를 가리킵니다.

\displaystyle

n은

n

표면 정상입니다.

양방향 반사율 분포 함수(BRDF; $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})$ r ( $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})$ i , $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})$ r $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})$ ) { $displaystyle f_{\text{r}},$ \ $obega$ _ ${\text{i}}})$ 는 불투명 표면에서 빛이 반사되는 방식을 정의하는 4개의 실제 변수의 함수입니다.실제 빛의 광학, 컴퓨터 그래픽 알고리즘 및 컴퓨터 비전 알고리즘에 사용됩니다.함수는 들어오는 빛 방향 , $\omega _{\text{i}}$ { \ $displaystyle$ \ $obega _$ { \ $text$ { i $\omega _{\text{i}}$ outgoing direction direction direction , $\omega _{\text{r}}$ direction r \ $displaystyle$ \ $obega _$ { \ $text$ { r $\omega _{\text{r}}$ } $\omega _{\text{r}}$ （ n \ $displaystyle$ \ $mathbf$ { n $\mathbf {n}$ } $}$ ） $\omega _{\text{r}}$ direction direction direction direction direction the the the,,,,,, the the the the the the the the the $\mathbf {n}$ the the the the the the the the the the the the the the the the the the the the where the the the the the the the the n n n n n n n n n nong $\omega _{\text{r}}$ to the irradiance incident on the surface from direction $\omega _{\text{i}}$ . Each direction $\omega$ is itself parameterized by azimuth angle $\phi$ and zenith angle $\theta$ , therefore the BRDF는 전체적으로 4가지 변수의 함수이다.BRDF에는 스테라디안(sr)이 입체 각도의 단위인 sr 단위가⁻¹ 있다.

정의.

BRDF는 ^[1]1965년경 Fred Nicodemus에 의해 처음 정의되었다.정의는 다음과 같습니다.

${\displaystyle f_{\text{r}}(\displaystyle _{\text{r}},\oferatorname {d},(\text{r})=,\frac {\text{r},(\operatorname {d}) L_{\text{r}},{\operatorname {d},{d})L_{\text{i}}({\text{i}})\cos \theta _{\text{i}},\operatorname {d} \opername {d} _{\text{i}}}})$

$L$ 서L(\ $displaystyle$ L $)$ 은 $L$ $E$ 방사광도 또는 단위당 단위당 단위당 단위당 단위당 단위당 단위당 단위당 단위당 단위당 단위당 단위당 단위당 전력은 방사광도 또는 단위 표면적당 전력이며, $\theta _{\text{i}}$ i $(\displaystyle$ \ $theta _{\texti})$ 는 $\theta _{\text{i}}$ $\$ $display$ i $(\displaystyle$ i $)$ $\omega _{\text{i}}$ 의 $\omega _{\text{i}}$ 입니다 $.$ }. 표면 $\omega _{\text{i}}$ $,$ $n$ ${displaystyle \mathbf$ $\mathbf {n}$ {n ${\text{i}}$ ${\text{r}}$ $}.$ $i$ 는 입사광을 나타내며 $, 지수$ r은 반사광을 $나타냅니다.$

함수가 미분량 사이의 지수로 직접 정의되지 않고 두 차분의 지수로 정의되는 이유는 d $\operatorname {d} E_{\text{i}}(\omega _{\text{i}})$ $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})$ $\operatorname {d} E_{\text{i}}(\omega _{\text{i}})$ ( $\operatorname {d} E_{\text{i}}(\omega _{\text{i}})$ i $\operatorname {d} E_{\text{i}}(\omega _{\text{i}})$ )(\ $display$ style \ $operatorname {d} E_{\text{i$ $이외$ 의 $\operatorname {d} E_{\text{i}}(\omega _{\text{i}})$ 조사광이 f r $)$ 에 관심이 $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})$ 때문이다. $displaystyle f_{\text{r}}(\text{i}},\operate_{\text{r$ 는 L $(\displaystyle L_{\text{r$ 에 의도하지 않은 $L_{\text{r}}(\omega _{\text{r}})$ 을 미치는 표면을 비추는 경우가 있습니다 $\operatorname {d} L_{\text{r}}(\omega _{\text{r}})$ $\operatorname {d} L_{\text{r}}(\omega _{\text{r}})$ displaystyle $\operatorname {d} L_{\text{r}}(\omega _{\text{r}})$ $(\text{$ $r}},$ $displaystyle$ { $},$ displaystyle { $r})$ $\operatorname {d} E_{\text{i}}(\omega _{\text{i}})$ ( $\operatorname {d} E_{\text{i}}(\omega _{\text{i}})$ i $\operatorname {d} E_{\text{i}}(\omega _{\text{i}})$ ) { $displaystyle \operatorname {d} E_{\text{i}}(오메가 _{\text{i}})$ } 。

관련 기능

공간적으로 가변적인 양방향 반사 분포 함수(SVDF)는 6차원 $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}},\,\mathbf {x} )$ f $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}},\,\mathbf {x} )$ ( $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}},\,\mathbf {x} )$ $i$ , $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}},\,\mathbf {x} )$ r $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}},\,\mathbf {x} )$ , $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}},\,\mathbf {x} )$ )입니다.\ $display f _$ { \ $text$ { $i }$ , \ $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}},\,\mathbf {x} )$ $mathb style$ $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}},\,\mathbf {x} )$

양방향 텍스처 함수(BTF)는 비평탄 표면 모델링에 적합하며 SVBRDF와 동일한 매개 변수화를 가지고 있지만 반대로 BTF는 그림자, 마스킹, 상호 반사 또는 지표면 산란과 같은 비국소 산란 효과를 포함한다.따라서 표면의 각 지점에서 BTF에 의해 정의된 함수를 외관 BRDF라고 합니다.

BSSRDF(Bidirectional Surface Satterrating Reflectance Distribution Function)는 더욱 일반화된 8차원 $S(\mathbf {x} _{\text{i}},\,\omega _{\text{i}},\,\mathbf {x} _{\text{r}},\,\omega _{\text{r}})$ S $S(\mathbf {x} _{\text{i}},\,\omega _{\text{i}},\,\mathbf {x} _{\text{r}},\,\omega _{\text{r}})$ i, $S(\mathbf {x} _{\text{i}},\,\omega _{\text{i}},\,\mathbf {x} _{\text{r}},\,\omega _{\text{r}})$ i $S(\mathbf {x} _{\text{i}},\,\omega _{\text{i}},\,\mathbf {x} _{\text{r}},\,\omega _{\text{r}})$ $S(\mathbf {x} _{\text{i}},\,\omega _{\text{i}},\,\mathbf {x} _{\text{r}},\,\omega _{\text{r}})$ r $,$ $S(\mathbf {x} _{\text{i}},\,\omega _{\text{i}},\,\mathbf {x} _{\text{r}},\,\omega _{\text{r}})$ r ) { $displaystyle$ S $(\mathbf {x} _{\texti},\mathbf})$ 입니다.다른 장소에서 나갈 수 있습니다.

이 모든 경우에서 빛의 파장에 대한 의존성은 무시되었습니다.실제로 BRDF는 파장에 의존하며 무지개 또는 발광 등의 효과를 고려하려면 파장에 대한 의존성이 명시되어야 합니다. $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})$ ( $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})$ i , $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})$ $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})$ , $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})$ , $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})$ , ${\$ r ) \ $display$ f $_$ { \ $text$ { $r$ } , \ $bda$ _ { \ $text$ { i } , \ $obda$ _ { \ text { i } , \ $da$ } , .모든 광학 요소가 선형인 일반적인 경우, 함수는 $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})=0$ 를 $\lambda _{\text{i}}=\lambda _{\text{r}}$ 하고 f r ( $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})=0$ $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})=0$ , $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})=0$ i , $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})=0$ $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})=0$ , $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})=0$ = r ) $=$ $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})=0$ ( $displaystyle f _$ { $\ text$ { $r }$ , , , \ $obsda$ _ { \ $text$ { $i$ } , , , , \ text { $i$ } , , , \ $\lambda _{\text{i}}=\lambda _{\text{r}}$ $_$ { $text$ { r } )에 $f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})=0$ . $\lambda _{\text{i}}=\lambda _{\text{r}}$ : 즉, 들어오는 빛과 동일한 파장에서만 빛을 방출합니다 $.$ 이 경우 f $f_{\text{r}}(\lambda ,\,\omega _{\text{i}},\,\omega _{\text{r}})$ " $f_{\text{r}}(\lambda ,\,\omega _{\text{i}},\,\omega _{\text{r}})$ , " $f_{\text{r}}(\lambda ,\,\omega _{\text{i}},\,\omega _{\text{r}})$ , " $f_{\text{r}}(\lambda ,\,\omega _{\text{i}},\,\omega _{\text{r}})$ ) { $displaystyle$ f $_$ { \ $text$ { $r$ } \ $lambda$ , , , \ $메가$ _ { \ text { $i$ } , , , \ $obega _$ { \ text { r} $}$ )로 $f_{\text{r}}(\lambda ,\,\omega _{\text{i}},\,\omega _{\text{r}})$ 할 수 있습니다.

물리 기반 BRDF

물리적으로 현실적인 BRDF에는 다음과 같은 추가 ^[2]특성이 있다.

$f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\geq 0$ 도: $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\geq 0$ r ( $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\geq 0$ i , $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\geq 0$ ) $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\geq 0$ 0 $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\geq 0$ { \ $displaystyle$ f _ { \ $text$ { $r$ } （ \ $text$ { i } , , , \ $메가 _$ { \ text { $r$ } ) \ $geq$ 0 $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\geq 0$ }
$f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})=f_{\text{r}}(\omega _{\text{r}},\,\omega _{\text{i}})$ 상호관계 준수: $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})=f_{\text{r}}(\omega _{\text{r}},\,\omega _{\text{i}})$ r ( $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})=f_{\text{r}}(\omega _{\text{r}},\,\omega _{\text{i}})$ i , $r$ r ) $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})=f_{\text{r}}(\omega _{\text{r}},\,\omega _{\text{i}})$ $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})=f_{\text{r}}(\omega _{\text{r}},\,\omega _{\text{i}})$ r ( $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})=f_{\text{r}}(\omega _{\text{r}},\,\omega _{\text{i}})$ r , $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})=f_{\text{r}}(\omega _{\text{r}},\,\omega _{\text{i}})$ i $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})=f_{\text{r}}(\omega _{\text{r}},\,\omega _{\text{i}})$ ) ( \ $displaystyle f _$ { \ $text$ { $i$ } , \ text { r } = $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})=f_{\text{r}}(\omega _{\text{r}},\,\omega _{\text{i}})$ f $_$ { \ text { r } （ $obega$ _ \ $text$ { r } } ） } = $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})=f_{\text{r}}(\omega _{\text{r}},\,\omega _{\text{i}})$ f $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})=f_{\text{r}}(\omega _{\text{r}},\,\omega _{\text{i}})$ _ { $\ text$ { r （ $obe$ _ { \ text { r ）（））） $f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})=f_{\text{r}}(\omega _{\text{r}},\,\omega _{\text{i}})$ 。
에너지 절약: $\forall \omega _{\text{i}},\,\int _{\Omega }f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\,\cos {\theta _{\text{r}}}d\omega _{\text{r}}\leq 1$ 、 $\forall \omega _{\text{i}},\,\int _{\Omega }f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\,\cos {\theta _{\text{r}}}d\omega _{\text{r}}\leq 1$ $\forall \omega _{\text{i}},\,\int _{\Omega }f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\,\cos {\theta _{\text{r}}}d\omega _{\text{r}}\leq 1$ r ( $i$ i , $\forall \omega _{\text{i}},\,\int _{\Omega }f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\,\cos {\theta _{\text{r}}}d\omega _{\text{r}}\leq 1$ r ) cos $\forall \omega _{\text{i}},\,\int _{\Omega }f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\,\cos {\theta _{\text{r}}}d\omega _{\text{r}}\leq 1$ 、 $\forall \omega _{\text{i}},\,\int _{\Omega }f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\,\cos {\theta _{\text{r}}}d\omega _{\text{r}}\leq 1$ d $\forall \omega _{\text{i}},\,\int _{\Omega }f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\,\cos {\theta _{\text{r}}}d\omega _{\text{r}}\leq 1$ 1 $\forall \omega _{\text{i}},\,\int _{\Omega }f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\,\cos {\theta _{\text{r}}}d\omega _{\text{r}}\leq 1$ \ $displaystyle$ \ $forall$ \ $obmega$ _ { \ $text$ { $i$ }, \ $int$ _ { \ Omega } $f_{$ \ text { $r$ }, \ $int$ _ { \ text { r}, cos $,$ ）

적용들

BRDF는 기본적인 방사선 측정 개념이므로 합성 장면의 사실적인 렌더링을 위한 컴퓨터 그래픽스(렌더링 방정식 참조) 및 객체 인식과 같은 많은 역방향 문제를 위한 컴퓨터 비전에도 사용됩니다.BRDF는 태양 전지(예: OPTOS 형식주의 사용) 또는 저농도 태양광 ^[3]^[4]발전 시스템의 빛 포획 모델링에도 사용되어 왔다.

위성 원격 감지의 맥락에서 NASA는 표면 반사율 이방성을 특징짓기 위해 BRDF 모델을 사용합니다.특정 토지 면적에 대해 BRDF는 표면 반사율의 선택된 다각형 관찰에 기초하여 확립된다.단일 관측치는 시야 기하학과 태양각에 따라 달라지지만, MODIS BRDF/Albedo 제품은 500m ^[5]분해능에서 여러 스펙트럼 대역의 고유 표면 특성을 설명한다.BRDF/Albedo 제품은 대기 산란에 따라 표면 알베도를 모델링하는 데 사용할 수 있습니다.

모델

BRDF는 보정된 카메라와 ^[6]광원을 사용하여 실제 물체에서 직접 측정할 수 있다. 그러나 컴퓨터 그래픽에서 자주 가정되는 램버트 반사율 모델을 포함하여 많은 현상학적 및 분석적 모델이 제안되었다.최신 모델의 유용한 기능은 다음과 같습니다.

적응 이방성 반사
소수의 직관적 매개 변수를 사용하여 편집 가능
방목 각도에서 플레넬 효과 설명
몬테카를로 방법에 적합하다.

W. Matusik 등은 측정된 샘플 사이에 보간하는 것이 현실적인 결과를 낳았고 이해하기 ^[7]쉽다는 것을 발견했다.

확산

광택이 나다

거울

다양한 빛-표면 ^[8]상호 작용을 모델링하는 데 사용할 수 있는 세 가지 요소.입사 광선은 검은색으로 표시되고 반사 광선은 BRDF에 의해 회색으로 모델링됩니다.

몇 가지 예

상수 BRDF에 의해 완벽하게 확산(물질)된 표면을 나타내는 램버트 모델.
롬멜-실리거, 달과 화성의 반사.
퐁 반사율 모델, 플라스틱과 유사한 ^[9]현상학적 모델입니다.
Blinn-Phong 모델은 Phong과 유사하지만 특정 양을 보간할 수 있어 계산 ^[10]오버헤드를 줄일 수 있습니다.
토런스-스파로 모델, 표면을 완벽하게 경사진 미세 ^[11]파사트의 분포로 나타내는 일반 모델.
쿡-토런스 모델, 파장과 그에 따른 색상 ^[12]변화를 설명하는 스펙큘러 마이크로패셋 모델(토런스-스파로).
(표면 ^[13]정규 분포 외에) 표면 접선 방향에 따라 타원-가우스 분포 함수가 있는 경면-마이크로페이스 모델입니다.
오렌-나야르 모델, 완전히 확산된(스펙트럼이 아닌) 마이크로패시트를 ^[14]가진 "방향 확산" 마이크로패시트 모델.
Ashikmin-Shirley 모델, 비경면 ^[15]아래의 확산 기판과 함께 이방성 반사율을 허용합니다.
HTSG(He, Torrance, Sillion, Greenberg)는 종합적인 물리 기반 ^[16]모델입니다.
적합 Lafortune 모형, 여러 개의 경엽이 있는 Phong의 일반화이며 측정된 데이터의 ^[17]모수 적합을 위한 것입니다.
분석 그리드 BRDF ^[18]근사치를 위한 Lebedev 모델.

획득

전통적으로 고니오레플렉토미터라고 불리는 BRDF 측정 장치는 하나 이상의 고니오메트릭 암을 사용하여 광원과 검출기를 측정할 물질의 평평한 샘플에서 다양한 방향으로 배치한다.전체 BRDF를 측정하려면 이 과정을 여러 번 반복해야 하며, 매번 광원을 이동하여 다른 입사각을 ^[19]측정해야 한다.안타깝게도 이러한 장치를 사용하여 BRDF를 조밀하게 측정하는 것은 시간이 많이 소요됩니다.이러한 기술의 첫 번째 개선점 중 하나는 반실버 미러와 디지털 카메라를 사용하여 평면 타깃의 많은 BRDF 샘플을 한 번에 채취했습니다.이 연구 이후, 많은 연구자가 실제 샘플로부터 BRDF를 효율적으로 획득하기 위한 다른 장치를 개발했으며, 여전히 활발한 연구 분야로 남아 있다.

HDR 영상을 기반으로 BRDF를 측정하는 다른 방법이 있습니다.표준 알고리즘은 영상에서 BRDF 포인트 클라우드를 측정하고 BRDF 모델 ^[20]중 하나로 최적화하는 것입니다.

BRDF 제작

BRDF 제작은 대상 BRDF의 측정 또는 합성 정보를 기반으로 표면을 구현하는 과정을 말한다.이러한 작업을 수행하는 방법은 세 가지가 있지만 일반적으로 다음 단계로 요약할 수 있습니다.

또는 합성한 대상 BRDF 분포 측정.
샘플의 이러한 분포로서 실현 가능하도록 연속적인.
이 분포(로 microfacet, 중간 명암)를 생산하는 기하학을 설계하라.
제조 절차에 관한 표면의 연속성과 매끄러움을 최적화합니다.

많은 접근법은 대상의 BRDF 제조를 위해:제안한 바 있다.

그 BRDF Milling:이 절차와 생성하는 microfacet 기하학과 BRDF 표본 분포로 시작한 다음이 나타나는데 최적화 측면에서 매끄럽고 연속성에 만난 한계의 밀링 머시인.는 기판의 마지막 BRDF 유통은 주름과 기계 가공 표면의 기하학.[21]

그 기하학과 잉크 선택의 최종 BRDF은 전체 효과이다.
: 위해서 공간적으로 다양한 BRDF(svBRDF)를 발생시키는데 목표 대상 BRDF. 금속 잉크의 알려진 BRDF는 알고리즘과 함께 한벌 선형적으로 목표 대상의 유통을 결합하지만 감안할 때 달성하기 위해 영역 매핑과 halftoning을 사용할 것이 제안되고 있는 BRDF 인쇄.지금까지 오직 또는 색-인쇄지만 현실 세계의 표면 인쇄, 이 소설 방법 인쇄 사진 더 현실적으로 도와 줄 수 있는 결과와 그들의 최종 외모에 영향을 미치specularity의 다른 양을 나타낼 수 있다.[22]
잉크와 기하학의 결합:.색과 specularity 외에 현실 세계의 사물들 또한 질감을 함유하고 있다.A3D프린터와 적절한 잉크로 표면을 커버하는 기하학을 제조하길, 최적으로, 잉크 조합을 선별하는 면을 만들어 이 방법 자유의 디자인과 더 정확한 BRDF 제작에 높은 수준을 줄 수가 있어 사용될 수 있다.[23]

「」를 참조해 주세요.

레퍼런스

^ Nicodemus, Fred (1965). "Directional reflectance and emissivity of an opaque surface". Applied Optics. 4 (7): 767–775. Bibcode:1965ApOpt...4..767N. doi:10.1364/AO.4.000767.
^ Duvenhage, Bernardt (2013). "Numerical verification of bidirectional reflectance distribution functions for physical plausibility". Proceedings of the South African Institute for Computer Scientists and Information Technologists Conference. pp. 200–208.
^ Andrews, Rob W.; Pollard, Andrew; Pearce, Joshua M. (2013). "Photovoltaic system performance enhancement with non-tracking planar concentrators: Experimental results and BDRF based modelling" (PDF). 2013 IEEE 39th Photovoltaic Specialists Conference (PVSC). pp. 0229–0234. doi:10.1109/PVSC.2013.6744136. ISBN 978-1-4799-3299-3. S2CID 32127698.
^ 앤드루스, 폴라드, 폴라드, 피어스, J.M., "논트래킹 평면 콘센트레이터에 의한 광전 시스템 성능 향상: 실험 결과와 양방향 반사 함수(BDRF) 기반 모델링", IEEE 저널, Pop166.DOI: 10.1109/JPHOTOV.2015.2478064
^ "BRDF/Albedo". NASA, Goddard Space Flight Center. Retrieved March 9, 2017.
^ Rusinkiewicz, S. "A Survey of BRDF Representation for Computer Graphics". Retrieved 2007-09-05.
^ Wojciech Matusik, Hanspeter Pister, Matt Brand, Leonard McMillan.데이터 중심 반사 모델.ACM Transactions on Graphics. 22(3) 2002.
^ "mental ray Layering Shaders".
^ B. T. Phong, Illumination for computer generated pictures, Communications of ACM 18 (1975), No. 6, 311–317.
^ James F. Blinn (1977). "Models of light reflection for computer synthesized pictures". Proc. 4th Annual Conference on Computer Graphics and Interactive Techniques. 11 (2): 192–198. doi:10.1145/563858.563893. S2CID 8043767.
^ K. 토런스와 E. 스패로우.거친 표면으로부터의 비경사 반사에 대한 이론.J. 옵티컬 SOC미국, 권 57. 1967. 페이지 1105–1114.
^ R. 쿡과 K.토랑스."컴퓨터 그래픽스의 반사율 모델"컴퓨터 그래픽스(SIGGRAPH '81 Proceedings), 제15권, 제3호, 1981년 7월, 페이지 301–316.
^ Ward, Gregory J. (1992). "Measuring and modeling anisotropic reflection". Proceedings of SIGGRAPH. pp. 265–272. doi:10.1145/133994.134078.
^ S.K. 나야와 M.오렌, "Lambertian 모델의 일반화 및 기계 비전에 대한 시사점"컴퓨터 비전에 관한 국제저널, 제14권, 제3호, 227~251쪽, 1995년 4월
^ Michael Ashikmin, Peter Shirley, An 이방성 Phong BRDF 모델, Journal of Graphics Tools 2000
^ X. He, K. Torrance, F. Silon, D.Greenberg, 광반사를 위한 포괄적인 물리적 모델, Computer Graphics 25(1991년), 아니요.연차 총회 시리즈, 175~186
^ E. 행운아, S.푸, K.토랑스, 그리고 D.그린버그, 반사율 함수의 비선형 근사.SIGGRAPH 97 Conference Procedures, 연례 Conference Series, 117–126페이지 편집자 Turner Whitted.ACM SIGGRAPH, 애디슨 웨슬리, 1997년 8월
^ Ilyn A., Levedev A., Sinyavsky V., Ignatenko, A., 평면 물체의 재료 반사 특성에 대한 이미지 기반 모델링(러시아어 ) 웨이백 머신에 2011-07-06 보관.입력: GraphiCon' 2009.; 2009. 페이지 198-201.
^ Marschner S.R., Westin S.H., Lafortune E.P.F., Torrance K.E., Greenberg D.P.(1999) 인체 피부를 포함한 이미지 기반 BRDF 측정.입력: Lischinski D., Larson G.W. (eds) Rendering Technics' 99.유로그래픽스빈, 스프링거
^ BRDFRecon 프로젝트 2011-07-06 Wayback Machine에서 아카이브
^ Weyrich, Tim; Peers, Pieter; Matusik, Wojciech; Rusinkiewicz, Szymon (2009). "Fabricating microgeometry for custom surface reflectance" (PDF). ACM SIGGRAPH 2009 Papers on - SIGGRAPH '09. New York, New York, USA: ACM Press: 1. doi:10.1145/1576246.1531338. ISBN 9781605587264. S2CID 13932018.
^ Matusik, Wojciech; Ajdin, Boris; Gu, Jinwei; Lawrence, Jason; Lensch, Hendrik P. A.; Pellacini, Fabio; Rusinkiewicz, Szymon (2009-12-01). "Printing spatially-varying reflectance". ACM Transactions on Graphics. 28 (5): 1–9. doi:10.1145/1618452.1618474.
^ Lan, Yanxiang; Dong, Yue; Pellacini, Fabio; Tong, Xin (2013-07-01). "Bi-scale appearance fabrication". ACM Transactions on Graphics. 32 (4): 1–12. doi:10.1145/2461912.2461989. ISSN 0730-0301. S2CID 4960068.

추가 정보

Lubin, Dan; Robert Massom (2006-02-10). Polar Remote Sensing. Volume I: Atmosphere and Oceans (1st ed.). Springer. p. 756. ISBN 978-3-540-43097-1.
Matt, Pharr; Greg Humphreys (2004). Physically Based Rendering (1st ed.). Morgan Kaufmann. p. 1019. ISBN 978-0-12-553180-1.
Schaepman-Strub, G.; M. E. Schaepman; T. H. Painter; S. Dangel; J. V. Martonchik (2006-07-15). "Reflectance quantities in optical remote sensing: definitions and case studies". Remote Sensing of Environment. 103 (1): 27–42. Bibcode:2006RSEnv.103...27S. doi:10.1016/j.rse.2006.03.002.

반사 모델과 BRDF의 개념에 대한 직관적인 소개.

[nicodemus_1965-1] Nicodemus, Fred (1965). "Directional reflectance and emissivity of an opaque surface". Applied Optics. 4 (7): 767–775. Bibcode:1965ApOpt...4..767N. doi:10.1364/AO.4.000767.

[Duvenhage_2013-2] Duvenhage, Bernardt (2013). "Numerical verification of bidirectional reflectance distribution functions for physical plausibility". Proceedings of the South African Institute for Computer Scientists and Information Technologists Conference. pp. 200–208.

[3] Andrews, Rob W.; Pollard, Andrew; Pearce, Joshua M. (2013). "Photovoltaic system performance enhancement with non-tracking planar concentrators: Experimental results and BDRF based modelling" (PDF). 2013 IEEE 39th Photovoltaic Specialists Conference (PVSC). pp. 0229–0234. doi:10.1109/PVSC.2013.6744136. ISBN 978-1-4799-3299-3. S2CID 32127698.

[4] 앤드루스, 폴라드, 폴라드, 피어스, J.M., "논트래킹 평면 콘센트레이터에 의한 광전 시스템 성능 향상: 실험 결과와 양방향 반사 함수(BDRF) 기반 모델링", IEEE 저널, Pop166.DOI: 10.1109/JPHOTOV.2015.2478064

[5] "BRDF/Albedo". NASA, Goddard Space Flight Center. Retrieved March 9, 2017.

[6] Rusinkiewicz, S. "A Survey of BRDF Representation for Computer Graphics". Retrieved 2007-09-05.

[7] Wojciech Matusik, Hanspeter Pister, Matt Brand, Leonard McMillan.데이터 중심 반사 모델.ACM Transactions on Graphics. 22(3) 2002.

[elementalBRDDs-8] "mental ray Layering Shaders".

[9] B. T. Phong, Illumination for computer generated pictures, Communications of ACM 18 (1975), No. 6, 311–317.

[10] James F. Blinn (1977). "Models of light reflection for computer synthesized pictures". Proc. 4th Annual Conference on Computer Graphics and Interactive Techniques. 11 (2): 192–198. doi:10.1145/563858.563893. S2CID 8043767.

[torrance_1967-11] K. 토런스와 E. 스패로우.거친 표면으로부터의 비경사 반사에 대한 이론.J. 옵티컬 SOC미국, 권 57. 1967. 페이지 1105–1114.

[12] R. 쿡과 K.토랑스."컴퓨터 그래픽스의 반사율 모델"컴퓨터 그래픽스(SIGGRAPH '81 Proceedings), 제15권, 제3호, 1981년 7월, 페이지 301–316.

[ward_1992-13] Ward, Gregory J. (1992). "Measuring and modeling anisotropic reflection". Proceedings of SIGGRAPH. pp. 265–272. doi:10.1145/133994.134078.

[14] S.K. 나야와 M.오렌, "Lambertian 모델의 일반화 및 기계 비전에 대한 시사점"컴퓨터 비전에 관한 국제저널, 제14권, 제3호, 227~251쪽, 1995년 4월

[15] Michael Ashikmin, Peter Shirley, An 이방성 Phong BRDF 모델, Journal of Graphics Tools 2000

[16] X. He, K. Torrance, F. Silon, D.Greenberg, 광반사를 위한 포괄적인 물리적 모델, Computer Graphics 25(1991년), 아니요.연차 총회 시리즈, 175~186

[17] E. 행운아, S.푸, K.토랑스, 그리고 D.그린버그, 반사율 함수의 비선형 근사.SIGGRAPH 97 Conference Procedures, 연례 Conference Series, 117–126페이지 편집자 Turner Whitted.ACM SIGGRAPH, 애디슨 웨슬리, 1997년 8월

[18] Ilyn A., Levedev A., Sinyavsky V., Ignatenko, A., 평면 물체의 재료 반사 특성에 대한 이미지 기반 모델링(러시아어 ) 웨이백 머신에 2011-07-06 보관.입력: GraphiCon' 2009.; 2009. 페이지 198-201.

[19] Marschner S.R., Westin S.H., Lafortune E.P.F., Torrance K.E., Greenberg D.P.(1999) 인체 피부를 포함한 이미지 기반 BRDF 측정.입력: Lischinski D., Larson G.W. (eds) Rendering Technics' 99.유로그래픽스빈, 스프링거

[20] BRDFRecon 프로젝트 2011-07-06 Wayback Machine에서 아카이브

[21] Weyrich, Tim; Peers, Pieter; Matusik, Wojciech; Rusinkiewicz, Szymon (2009). "Fabricating microgeometry for custom surface reflectance" (PDF). ACM SIGGRAPH 2009 Papers on - SIGGRAPH '09. New York, New York, USA: ACM Press: 1. doi:10.1145/1576246.1531338. ISBN 9781605587264. S2CID 13932018.

[22] Matusik, Wojciech; Ajdin, Boris; Gu, Jinwei; Lawrence, Jason; Lensch, Hendrik P. A.; Pellacini, Fabio; Rusinkiewicz, Szymon (2009-12-01). "Printing spatially-varying reflectance". ACM Transactions on Graphics. 28 (5): 1–9. doi:10.1145/1618452.1618474.

[23] Lan, Yanxiang; Dong, Yue; Pellacini, Fabio; Tong, Xin (2013-07-01). "Bi-scale appearance fabrication". ACM Transactions on Graphics. 32 (4): 1–12. doi:10.1145/2461912.2461989. ISSN 0730-0301. S2CID 4960068.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

Search

양방향 반사율 분포 함수

네임스페이스

더

목차

정의.

관련 기능

물리 기반 BRDF

적용들

모델

몇 가지 예

획득

BRDF 제작

「」를 참조해 주세요.

레퍼런스

추가 정보

Search

양방향 반사율 분포 함수

정의.

관련 기능

물리 기반 BRDF

적용들

모델

몇 가지 예

획득

BRDF 제작

「 」를 참조해 주세요.

레퍼런스

추가 정보

「」를 참조해 주세요.