부폰의 바늘 문제

바늘은 선을 가로지르는 반면 b 바늘은 그렇지 않다.

수학에서 부폰의 바늘 문제는 18세기에 조르주-루이 르클레르, 콤테 드 부폰에 의해 처음 제기되었던 질문이다.^[1]

우리가 각각 같은 폭의 평행한 나무 조각으로 된 바닥이 있다고 가정해봅시다. 그리고 우리는 바닥에 바늘을 떨어뜨립니다. 바늘이 두 가닥 사이의 선에 걸쳐 있을 확률은 얼마인가?

부폰의 바늘은 기하학적 확률에서 가장 초기 문제였다;^{[according to whom?]} 그것은 통합된 기하학을 사용하여 해결할 수 있다. Needle 길이 l가 스트립의 폭 t보다 크지 않은 경우, 원하는 확률 p에 대한 해법은 다음과 같다.

p={\frac {2}{\pi }}{\frac {l}{t}}}.

이것은 비록 그것이 데 부폰의 질문에 대한 원래 동기는 아니었지만 숫자 π의 근사치를 위한 몬테카를로 방법을 설계하는 데 사용될 수 있다.^[2]

해결책

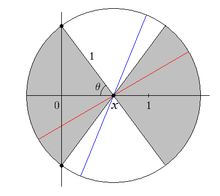
좀 더 수학적인 용어의 문제는: 평행선 t 단위가 떨어져 있는 평면에 떨어진 길이 l $l$ 의 $l$ 바늘을 볼 때, 바늘이 착지할 때 선에 걸쳐 놓여질 확률은 얼마인가?

x는 바늘의 중심에서 가장 가까운 평행선까지의 거리가 되게 하고, θ은 바늘과 평행선 중 하나 사이의 급성 각이 되게 한다.

0과 t /2 사이의 x의 균일한 확률밀도함수는

{\frac {2}{t}:\ 0\leq x\leq {\frac}{2}}\\0&::{\text{data.}}}}\end{case}

여기서 x = 0은 선에 직접 중심을 맞춘 바늘을, x = t/2는 두 선 사이에 완벽하게 중심을 맞춘 바늘을 나타낸다. 균일한 PDF는 바늘이 이 범위 어디든 떨어질 가능성이 동일하지만, 바늘 밖으로 떨어질 수는 없다고 가정한다.

0과 π/2 사이의 θ의 균일한 확률밀도함수는

{\pi{case}{\frac {2}{\pi }:\ 0\leq \theta \leq {\frac {}{2}}\\0&::{\text{data.}}}}\end{case}

여기서 θ = 0 라디안은 표시된 선과 평행한 바늘을 나타내며, π = 2/2 라디안은 표시된 선에 수직인 바늘을 나타낸다. 이 범위 내의 모든 각도는 동등한 가능성이 있는 결과를 가정한다.

x와 θ의 두 변수는 독립적이므로 관절 확률밀도함수가 산물이다.

{\pi{case}{\frac {4}{t\}}:\ 0\leq x\leq {\frac {t}{2}},\\\leq \teta \leq {\\frac {}{2}}\pi\0&::{\text{data.}}}}\end{case}

만약 바늘이 선을 넘는다면

x\leq {\frac {l}{2}}\sin \theta .

이제 두 가지 사건이 있다.

사례 1: 짧은 바늘

관절 확률밀도함수를 통합하면 바늘이 선을 넘을 확률을 얻을 수 있다.

P=\int _{\theta =0}^{\frac {\pi }{2}}\int _{x=0}^{(l/2)}\sin \teta }{\frac}{4}{t\pi }\d\d\teta ={\fr}{2l}}{t\pi\pi}}.

사례 2: 긴 바늘

$l>t$ > $l>t$ $l>t$ 을(를) 가정해 보자 $l>t$ 이 경우 접합 확률밀도함수를 통합하여 다음을 얻는다.

\int_{\theta =0}^{\frac {}{2}}\int_{x=0}^{m(\theta )}{\frac {4}{t\pi }\,d\\d\teta ,

여기서 $m(\theta )$ ( $m(\theta )$ ) ${\displaystyle$ m $(\theta )}$ 은 $(l/2)\sin \theta$ / 2) $(l/2)\sin \theta$ $(l/2)\sin \theta$ $(l/2)\sin \theta$ $(l/2)\sin \theta$ 과 $(l/2)\sin\theta$ t $t/2$ / $t/2$ ${\displaystyty t/2}$ 사이의 최소값이다 $m(\theta)$ $t/2$

따라서 위의 통합을 수행하면 $t<l$ < $t<l$ ${\displaystyle t<l})$ 에서 $t<l$ 바늘이 선을 넘을 확률은

{\frac {2l}{t\pi }-{\frac {2}{t\pi }}\{\\sqrt {l^{2}-t^{2}}+t\in ^{-1}\{-1}\l}\right\}+1

또는

{\frac{2}{\pi }}\cos ^{-1}{\frac {t}{l}}+{\frac {2}{\pi }}{{\frac}}}}{1-{1-{1-\sqrt}\{l}}}\rig}}}.

두 번째 표현에서 첫 번째 항은 바늘의 각도가 항상 최소한 하나의 선을 넘을 확률을 나타낸다. 오른쪽 항은 바늘이 위치가 중요한 각도로 떨어져 선을 넘을 확률을 나타낸다.

Alternatively notice that whenever $\theta$ has a value such that $l\sin \theta \leq t$ , that is, in the range $0\leq \theta \leq \sin ^{-1}(t/l)$ the probability of crossing is the same as in the short needle case. 그러나 $l\sin \theta >t$ $l\sin \theta >t$ $⁡$ $l\sin \theta >t$ > $l\sin \theta >t$ ${\displaystyle l\sin \theta$ > $t$ 즉 $\sin ^{-1}(t/l)<\theta \leq {\frac {\pi }{2}}$ - $\sin ^{-1}(t/l)<\theta \leq {\frac {\pi }{2}}$ ⁡ $\sin ^{-1}(t/l)<\theta \leq {\frac {\pi }{2}}$ ( $\sin ^{-1}(t/l)<\theta \leq {\frac {\pi }{2}}$ / l $\sin ^{-1}(t/l)<\theta \leq {\frac {\pi }{2}}$ ) $\sin ^{-1}(t/l)<\theta \leq {\frac {\pi }{2}}$ 2 ${\$ ^-1 $(t/l)<\tetaq {\frac {\pi }{2$ }} 확률은 $\sin ^{-1}(t/l)<\theta \leq {\frac {\pi }{2}}$ 일정하며 1과 같다.

\left(\int _{\theta =0}^{\sin ^{-1}(t/l)}\int _{x=0}^{(l/2)\sin \theta }{\frac {4}{t\pi }}\right)+\left(\int _{\sin ^{-1}(t/l)}^{\frac {\pi }{2}}{\frac {2}{\pi }}\right)={\frac {2l}{t\pi }}-{\frac {2}{t\pi }}\left\{{\sqrt {l^{2}-t^{2}}}+t\sin ^{-1}\left({\frac {t}{l}}\right)\right\}+1

기초 미적분 사용

"짧은 바늘" 케이스에 대한 다음 솔루션은 위와 동일하지만, 더 시각적인 풍미를 가지며, 반복적인 통합을 방지한다.

We can calculate the probability $P$ as the product of 2 probabilities: $P=P_{1}\cdot P_{2}$ , where $P_{1}$ is the probability that the center of the needle falls close enough to a line for the needle to possibly cross it, and ${\displayst$ $yle P_{2}}:$ 중심부가 도달 범위 내에 있다는 점을 감안할 때 바늘이 실제로 선을 통과할 확률이다 $P_{2}$ .

위 섹션의 그림을 보면 바늘의 중심이 스트립의 어느 한 쪽의 $l/2$ / $l/2$ ${\디스플레이$ 스타일 $l/2}$ 단위 $l/2$ 내에 있으면 바늘이 선을 넘을 수 있다는 것이 명백하다. ${\frac {l}{2}}+{\frac {l}{2}}$ ${\frac {l}{2}}+{\frac {l}{2}}$ + ${\frac {l}{2}}+{\frac {l}{2}}$ ${\frac {l}{2}}+{\frac {l}{2}}$ ${\fracystyle {\$ frac{ $l}{2}}+{\frac$ { $l}{2}}}$ 을 $\frac{l}{2}+\frac{l}{2}$ 양쪽에서 추가하고 전체폭 $t$ {\ $displaystyle$ t $}$ 로 $P_{1}={\frac {l}{t}}.$ P $P_{1}={\frac {l}{t}}.$ $P_{1}={\frac {l}{t}}.$ $P_{1}={\frac {l}{t}}.$ . $P_{1}={\frac {l}{t}}.$ {\ $displaystyle P_{$ 1}={\ $frac$ { $l}{t$ }}{t $}}}.$ $}$

빨강과 파랑의 바늘은 모두 x를 중심으로 한다. 빨간색은 양쪽에 2㎛ 각도로 들어 있는 회색 영역 안에 들어가므로 수직선을 가로지르고, 파란색은 그렇지 않다. 회색인 원의 비율은 중심 x가 0에서 1로 이동할 때 우리가 통합하는 것이다.

이제 중심은 스트립의 가장자리의 손이 닿는 곳에 있다고 $P_{2}$ 하고, P $P_{2}$ ${\$ 계산을 간소화하기 위해 $l=2$ = $l=2$ $l=2$ 라고 가정할 수 있다 $l=2$

x와 θ을 이 절의 그림과 같이 두십시오. 바늘의 중심을 x에 놓고, 바늘이 가능한 방향의 π 라디안 중에서 2㎛ 라디안의 범위 안에 들면 수직축을 가로지른다. 이것은 그림에서 x의 왼쪽에 있는 회색 영역을 나타낸다. 고정 x의 경우, we $\theta \left(x\right)=\cos ^{-1}\left(x\right)$ ) $\theta \left(x\right)=\cos ^{-1}\left(x\right)$ = $\theta \left(x\right)=\cos ^{-1}\left(x\right)$ - $\theta \left(x\right)=\cos ^{-1}\left(x\right)$ ) ${\$ cos $\theta \left(x\right)=\cos ^{-1}\left(x\right)$ ^{-1}. 이제 x를 0에서 1로 이동시키고, 다음과 같이 통합할 수 있다.

P_{2}=\int _{0}^{1}{\frac {2\theta (x)}{\pi }}\,dx={\frac {2}{\pi }}\int _{0}^{1}\cos ^{-1}(x)\,dx={\frac {2}{\pi }}\cdot 1={\frac {2}{\pi }}.

두 결과를 곱하면 $P=P_{1}\cdot P_{2}={\frac {l}{t}}{\frac {2}{\pi }}={\frac {2l}{t\pi }}$ 와 $P=P_{1}\cdot P_{2}={\frac {l}{t}}{\frac {2}{\pi }}={\frac {2l}{t\pi }}$ $P=P_{1}\cdot P_{2}={\frac {l}{t}}{\frac {2}{\pi }}={\frac {2l}{t\pi }}$ = $P=P_{1}\cdot P_{2}={\frac {l}{t}}{\frac {2}{\pi }}={\frac {2l}{t\pi }}$ P 1 $P=P_{1}\cdot P_{2}={\frac {l}{t}}{\frac {2}{\pi }}={\frac {2l}{t\pi }}$ $P=P_{1}\cdot P_{2}={\frac {l}{t}}{\frac {2}{\pi }}={\frac {2l}{t\pi }}$ $P=P_{1}\cdot P_{2}={\frac {l}{t}}{\frac {2}{\pi }}={\frac {2l}{t\pi }}$ = $P=P_{1}\cdot P_{2}={\frac {l}{t}}{\frac {2}{\pi }}={\frac {2l}{t\pi }}$ t $P=P_{1}\cdot P_{2}={\frac {l}{t}}{\frac {2}{\pi }}={\frac {2l}{t\pi }}$ 2 $P=P_{1}\cdot P_{2}={\frac {l}{t}}{\frac {2}{\pi }}={\frac {2l}{t\pi }}$ = 2 l $P=P_{1}\cdot P_{2}={\frac {l}{t}}{\frac {2}{\pi }}={\frac {2l}{t\pi }}$ = 2 l $P=P_{1}\cdot P_{2}={\frac {l}{t}}{\frac {2}{\pi }}={\frac {2l}{t\pi }}$ ${\$ { $l}{t}{{l$ }}{\ $pi }}={\frac {2l}{t\pi$ 을 얻는다.

"짧은 바늘 케이스"를 계산하는 훨씬 더 우아하고 간단한 방법이 있다. 니들 끝은 해당 지역에 인접한 두 라인 중 하나에서 가장 멀리 떨어진 곳에 위치해야 하며, 이 라인에서 수평( $l\cos \theta$ 에 수직) 거리 내에 위치해야 한다 $($ 여기서 ne {\ $displaystyle \theta$ $}$ 은(여기서 $\theta$ ${\displaystyle$ \ $theta$ }은 $\theta$ 니들과 수평 사이의 각도임).비틀거리며 건너다 바늘의 이 끝이 이 선에서 수평으로 이동할 수 있는 가장 먼 $t$ 은 t ${\displaystyle$ t $}$ 이다 $t$ Needle의 $t$ 가장 먼 끝부분이 0 $0\leq \theta \leq \pi /2$ ≤ $l\cos \theta$ $l\cos \theta$ needle crosses crosses that ${$ {\ $displaystyle l$ $\cos \theta$ $}$ 선에서 $l\cos \theta$ (따라서 바늘이 선을 가로지르는) $0\leq \theta \leq \pi /2$ $l\cos \theta$ $0\leq \theta \leq \pi /2$ / $0\leq \theta \leq \pi /2$ {\ $displaystystyleq \leq \pi2}$ 의 영역 내에서 이동할 수 있는 확률 $0\leq \theta \leq \pi /2$ 에 의해 주어지는.

${\displaystyle P={\frac {\int _{0}^{\frac {\pi }{2}}l\cos \theta d\theta }{\int _{0}^{\frac {\pi }{2}}td\theta }}={\frac {l}{t}}{\frac {\int _{0}^{\frac {\pi }{2}}\cos \theta$ $d\theta }{\int _{0}^{$ 0}^{\ $frac {}{2}}d\tea}}}={\frac$ {1 $}{\frac$ { $1}{{\pi }}}}}}}{\frac {2l}{t\pi$

통합 없음

짧은 니들 문제는 또한 어떤 통합 없이 해결될 수 있는데, 직경 t의 원이 정확히 두 지점에서 항상 t 스트립을 가로지른다는 기하학적 사실(즉 확률 1)으로부터 p의 공식을 설명하는 방법으로 해결할 수 있다. 이 해결책은 1860년^[3] 조셉 에밀 바비에에 의해 주어졌으며 "버폰 국수"라고도 불린다.

추정 π

π을 찾기 위한 실험. 길이가 9제곱인 성냥은 너비가 9제곱인 행 사이에 17번 던져졌고, 11개의 성냥은 그린 포인트로 표시된 그려진 선을 가로질러 무작위로 착지했다.
(2l·n)/(th)=(2·9·17)/(9·11)≈3.1≈π.

매개변수 t = 5.0, l = 2.6으로 Buffon의 바늘 실험을 스케치하기 위해 Matplotlib를 사용한 Python 3 기반 시뮬레이션. 토스(x축) 횟수가 무한대에 가까워질 때 3.14에 근접하는 Pi(y축)의 계산값을 관찰한다.

위의 간단한 첫 번째 사례에서 확률 $P$ $P$ 에 대해 얻은 공식은 다음과 같이 재배열할 수 있다 $P$ .

\pi ={\frac {2l}{t.P}

따라서

P

P

을(를) 추정하는 실험을 한다면 π에 대한 추정치도 얻을 수 있을 것이다

P

바늘을 떨어뜨려 그 바늘 중 h가 선을 가로지르고 있다는 것을 발견했다고 가정해 봅시다. $h/n$ P $P$ 는 분율 h $h/n$ $h/n$ 에 의해 근사치가 된다 $P$ $h/n$ 이렇게 하면 공식은 다음과 같다.

\pi \ 약 {\frac {2l\cdot n}{th}}.

1901년 이탈리아의 수학자 마리오 라자리니(Mario Lazzarini)가 부폰의 바늘 실험을 했다. 바늘을 3408번 던지며, π에 대해 잘 알려진 근사치 355/113을 얻어 소수점 6자리까지 정확했다.^[4] 이미 잘 알려진 근사치 355/113(사실 분자와 분모에 5자리 이하인 합리적 근사치가 없음)을 복제하기 위해 설정된 라자리니 '실험'은 확인편향의 예로서, 임상시험 횟수에서 예상한 것보다 더 정확한 π의 '예상'을 산출한다. 다음과 같다.

라자리니는 길이가 나무 줄기의 너비의 5/6인 바늘을 골랐다. 이 경우 바늘이 선을 넘을 확률은 5 $㎛{\$ 이므로 바늘을 떨어뜨려 x교차를 얻으려면 as을 다음과 같이 추정할 것이다 ${\textstyle {\frac {5}{3\pi }}}$

\pi \pi \약 {5}{3}}\cdot {\frac {n}{x}}}

그래서 라자리니가 355/113의 결과를 노리고 있다면, 다음과 같은 n과 x가 필요했다.

{\frac {355}{355}}={\frac {5}{3}}\cdot {\frac {n}{x}}}}}

또는 동등하게

x={\frac {frac}{213}}.

이를 위해서는 n을 213의 배수로 선택해야 하는데, 그 이유는

{\textstyle {\frac {113n}{213}}}

n

{\textstyle {\frac {113n}{213}}}

{\

이(가) 정수이고

{\textstyle {\frac {113n}{213}}}

, 한 개는 바늘을 떨어뜨리고,

{\textstyle x={\frac {113n}{213}}}

x

{\textstyle x={\frac {113n}{213}}}

=

{\textstyle x={\frac {113n}{213}}}

{\textstyle x={\frac {113n}{213}}}

{\

의

{\textstyle x={\frac {113n}{213}}}

성공을 바라기 때문이다. 213개의 바늘을 떨어뜨려 113개의 성공을 거두면 소수점 6자리까지 정확한 accurate의 추정치를 의기양양하게 보고할 수 있다. 만약 그렇지 않다면, 213번의 실험을 더 할 수 있고, 총 226번의 성공을 바랄 수 있고, 그렇지 않다면, 필요에 따라 반복할 수 있다. 라자리니는 3408 = 213 · 16번의 실험을 실시하여, 이것이 그가 '추정'을 얻기 위해 사용한 전략일 가능성이 있어 보인다.

전술에 대한 위의 설명은 심지어 라자리니에게 자비로운 것으로 여겨질 수도 있다. 그가 더 적은 토스를 위해 보고한 중간 결과에 대한 통계적 분석은 실험을 통해 기대치에 대한 그러한 근접 합의를 달성할 확률을 매우 낮게 이끈다. 이것은 "실험" 자체가 물리적으로 수행된 것이 아니라, 통계적 기대치에 부합하기 위해 상상력으로부터 만들어진 숫자에 근거한 것일 수 있지만, 밝혀진 바와 같이, 너무 잘 이루어졌다는 것을 매우 가능하게 한다.^[5]

그러나 네덜란드의 과학 저널리스트 한스 반 마넨은 라자리니 기사의 기사는 라자리니 기고가 (학교 교사들을 대상으로 한) 독자들에게는 설명대로 작동할 수 없다는 것이 상당히 명백했을 것이기 때문에 그렇게 심각하게 받아들여질 의도는 결코 아니었다고 주장한다.^[6]

참고 항목

참조

^ 드 l'Academy 로이 데스 과학(1733), 43–45; 자연, 제네랄 외 미립자 (1777), 페이지 46.
^ Behrends, Ehrhard. "Buffon: Hat er Stöckchen geworfen oder hat er nicht?" (PDF). Retrieved 14 March 2015.
^ Aigner, Martin; Ziegler, Günter M. (2013). Proofs from THE BOOK (2nd ed.). Springer Science & Business Media. pp. 189–192.
^ Lazzarini, M. (1901). "Un'applicazione del calcolo della probabilità alla ricerca sperimentale di un valore approssimato di π" [An Application of Probability Theory to Experimental Research of an Approximation of π]. Periodico di Matematica per l'Insegnamento Secondario (in Italian). 4: 140–143.
^ ^a ^b 리 오소리, '라자리니 행운의 approx' 수학잡지 67, 1994, 83–91.
^ 한스 판 마넨, '헤트 스토크제 판 라자리니'(라자리니 스틱), '스케프터' 31.3, 2018.

참고 문헌 목록

Badger, Lee (April 1994). "Lazzarini's Lucky Approximation of π". Mathematics Magazine. Mathematical Association of America. 67 (2): 83–91. doi:10.2307/2690682. JSTOR 2690682.
Ramaley, J. F. (October 1969). "Buffon's Noodle Problem". The American Mathematical Monthly. Mathematical Association of America. 76 (8): 916–918. doi:10.2307/2317945. JSTOR 2317945.
Mathai, A. M. (1999). An Introduction to Geometrical Probability. Newark: Gordon & Breach. p. 5. ISBN 978-90-5699-681-9.
Dell, Zachary; Franklin, Scott V. (September 2009). "The Buffon-Laplace needle problem in three dimensions". Journal of Statistical Mechanics: Theory and Experiment. 2009 (9): 010. Bibcode:2009JSMTE..09..010D. doi:10.1088/1742-5468/2009/09/P09010.
슈뢰더, L. (1974년) "부폰의 바늘 문제: 많은 수학 개념을 흥미롭게 적용했다"고 말했다. 수학 교사, 67(2), 183–6.

외부 링크

부폰의 바늘 문제
수학 서프라이즈: 부폰 국수
MSE: 버폰의 바늘
부폰 니들 자바 애플릿
PI 시각화(플래시) 추정
Buffon의 바늘: 슬라이드쉐어에서의 재미와 기본(프레젠테이션)
R패키지 애니메이션을 이용한 이하이시에의 부폰 니들 시뮬레이션 애니메이션
Jeffrey Ventrella의 3D 물리적 애니메이션
Padilla, Tony. "Π Pi and Buffon's Needle". Numberphile. Brady Haran. Archived from the original on 2013-05-17. Retrieved 2013-04-09.

[1] 드 l'Academy 로이 데스 과학(1733), 43–45; 자연, 제네랄 외 미립자 (1777), 페이지 46.

[2] Behrends, Ehrhard. "Buffon: Hat er Stöckchen geworfen oder hat er nicht?" (PDF). Retrieved 14 March 2015.

[3] Aigner, Martin; Ziegler, Günter M. (2013). Proofs from THE BOOK (2nd ed.). Springer Science & Business Media. pp. 189–192.

[4] Lazzarini, M. (1901). "Un'applicazione del calcolo della probabilità alla ricerca sperimentale di un valore approssimato di π" [An Application of Probability Theory to Experimental Research of an Approximation of π]. Periodico di Matematica per l'Insegnamento Secondario (in Italian). 4: 140–143.

[Badger1994-5] 리 오소리, '라자리니 행운의 approx' 수학잡지 67, 1994, 83–91.

[vMaanen2018-6] 한스 판 마넨, '헤트 스토크제 판 라자리니'(라자리니 스틱), '스케프터' 31.3, 2018.

[1]

[2]

[3]

[4]

[5]

[6]

Search