캐시-관심 알고리즘

컴퓨팅에서 캐시불변 알고리즘(혹은 캐시불변 알고리즘)은 명시적 매개변수로 캐시 크기(혹은 캐시 라인의 길이 등)를 갖지 않고 프로세서 캐시를 이용하도록 설계된 알고리즘이다.최적의 캐시불변 알고리즘은 캐시를 최적으로 사용하는 캐시불변 알고리즘이다(증상증적 의미에서는 상수요인을 무시함).따라서 캐시 취약 알고리즘은 서로 다른 캐시 크기를 가진 여러 컴퓨터 또는 서로 다른 크기의 캐시 수준을 가진 메모리 계층 구조에서 수정 없이 잘 수행하도록 설계된다.캐시 모호한 알고리즘은 명시적 루프 타일링과 대조되며, 이는 문제를 특정 캐시에 대해 최적의 크기의 블록으로 명시적으로 구분한다.null

최적의 캐시 취약 알고리즘은 매트릭스 곱하기, 매트릭스 전환, 정렬 및 기타 몇 가지 문제로 알려져 있다.Cooly-와 같은 몇 가지 일반적인 알고리즘Tukey FFT는 파라미터의 특정 선택사항에서는 최적으로 캐시에 민감하다.이러한 알고리즘은 무증상적 의미(상수 요인 무시)에서만 최적이기 때문에, 절대적 의미에서의 거의 최적의 성능을 얻기 위해 추가적인 기계별 튜닝이 필요할 수 있다.캐시 모호한 알고리즘의 목표는 필요한 튜닝의 양을 줄이는 것이다.null

일반적으로 캐시 취약 알고리즘은 재귀적 분할 및 변환 알고리즘에 의해 작동하며, 여기서 문제는 더 작은 하위 문제로 나뉜다.결국 캐시 크기에 상관없이 캐시에 맞는 하위 문제 크기에 도달하게 된다.예를 들어, 최적의 캐시 취약 매트릭스 곱셈은 각 매트릭스를 4개의 하위 매트릭스로 재귀적으로 분할하여, 하위 매트릭스를 깊이 우선 방식으로 곱하여 얻는다.^{[citation needed]}특정 기계를 튜닝할 때, 하단 레벨에서 특정 캐시 크기에 맞게 튜닝된 루프 타일링을 사용하는 하이브리드 알고리즘을 사용할 수 있지만, 그렇지 않은 경우 캐쉬-관심 알고리즘을 사용할 수 있다.null

역사

캐시 탐욕 알고리즘에 대한 아이디어(및 이름)는 찰스 E에 의해 고안되었다. Leiserson은 일찍이 1996년에 Harald Prokop에 의해 1999년 매사추세츠 공과대학의 석사학위 논문에서 처음 발표되었다.^[1]전형적으로 특정한 문제를 분석하는 전임자들이 많았다; 이것들은 Frigo et al. 1999에서 자세히 논의되었다.초기 사례로는 재귀적인 Fast Fourier Transform을 위한 Singleton 1969, Aggarwal et al. 1987의 유사한 아이디어, Matrix 곱셈과 LU 분해를 위한 Frigo 1996, Blitz++ 라이브러리의 Matrix 알고리즘을 위한 Todd Veldhuizen 1996 등이 있다.null

이상화된 캐시 모델

일반적으로 프로그램은 캐시에 더 민감하게 만들 수 있다.^[2]

• 알고리즘이 동일한 메모리 조각을 여러 번 가져오는 시간적 위치
• 공간적 인접성 - 후속 메모리 액세스가 인접하거나 메모리 주소 근처에 있는 경우.

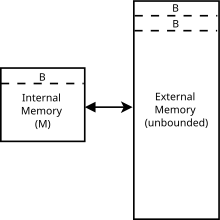
캐쉬-관심 알고리즘은 캐쉬-관심 모델이라고도 하는 이상적인 캐쉬 모델을 사용하여 분석한다.이 모델은 실제 캐시의 특성(연관성, 대체 정책 등)보다 분석하기가 훨씬 쉽지만, 많은 경우 보다 현실적인 캐시의 성능이라는 일정한 요인 내에 있을 수 있다.캐쉬-관심 알고리즘이 블록 크기나 캐시 크기를 모르기 때문에 외부 메모리 모델과 다르다.null

특히 캐쉬에 민감한 모델은 추상적인 기계(즉, 연산의 이론적 모델)이다.튜링머신의 무한테이프를 무한 어레이로 대체하는 RAM머신 모델과 비슷하다.어레이 내의 각 위치는 실제 컴퓨터의 임의 액세스 메모리와 유사하게 $O{\displaystyle }$( ${\displaystyle 1}$) ${\displaystyle$ O$(1)}$번으로$$ 액세스할 수 있다.RAM 머신 모델과 달리 RAM과 CPU 사이의 두 번째 스토리지 레벨인 캐시를 도입하기도 한다.두 모델 간의 다른 차이점은 아래에 열거되어 있다.캐시 취약성 모델에서:

• 메모리는 각각 $B{\displaystyle }$ ${\displaystyle B}$개의$$ 객체 블록으로 나뉜다.
• 이제 메인 메모리와 CPU 레지스터 사이의 로드 또는 저장소가 캐시에서 서비스될 수 있다.
• 캐시로부터 로드나 스토어를 서비스할 수 없는 경우 캐시 미스라고 한다.
• 캐시 누락으로 인해 하나의 블록이 메인 메모리에서 캐시로 로드된다.즉, CPU가 $w{\displaystyle }$ ${\displaystyle w}$ $및$ x ${\displaystyle$ x$}$에 $액세스하려고$ 하면 w ${\displaystyle$ $w$$}$을(를$)$ 포함하는 행인 경우$$ $x{\displaystyle }$ ${\displaystyle$ x$}$이(가) 캐시에 로드된다$$.이전에 캐시가 가득 찼을 경우 라인도 제거된다(아래 교체 정책 참조).
• 캐시에는 $M{\displaystyle }$ ${\displaystyle M}$개체가$$ 저장되며 여기서 $M{\displaystyle }$= ${\displaystyle \mathrm{\Omega }}$(${\displaystyle {B\mathrm{}}^{}}$2${\displaystyle {}^{}}$) ${\displaystyle$ M$=\Oomega(B^{2})}$.이것은 또한 높은 캐시 가정으로도 알려져 있다.
• 캐시는 완전히 연관되어 있다. 각 줄은 캐시의 어느 위치에나 로드될 수 있다.^[3]
• 대체 정책이 최적이다.즉, 캐시에 알고리즘 실행 중 메모리 액세스 전체 시퀀스가 주어지는 것으로 가정한다.$시간{\displaystyle }$ t {\$displaystyle$ t$}$에서 회선을 제거해야 할 경우, 향후의 요청 순서를 조사하고, 향후 가장 멀리 접근하는 회선을 제거한다$.$이는 오프라인 최적 교체 전략의^[4][5] 작은 상수 요소 내에 있는 것으로 보이는 가장 최근에 사용한 정책을 통해 실제 에뮬레이션할 수 있다.

캐쉬에 민감한 모델 내에서 실행되는 알고리즘의 복잡성을 측정하기 위해 알고리즘이 경험하는 캐시 누락 수를 측정한다.모델은 캐시의 요소에 접근하는 것이 메인 메모리의 사물에 접근하는 것보다 훨씬 빠르다는 사실을 포착하기 때문에 알고리즘의 실행 시간은 캐시와 메인 메모리 사이의 메모리 전송 수에 의해서만 정의된다.이는 위의 모든 기능이 있는 외부 메모리 모델과 유사하지만 캐쉬-관심 알고리즘은 캐시 매개변수(${\displaystyle }$ ${\displaystyle B}$ 및 M$$ ${\displaystyle$ M$})$^[6]와 $독립적$이다.그러한 알고리즘의 이점은 캐쉬가 많은 기계에서 효율적인 것이 특정 실제 기계 매개변수에 대해 미세 조정하지 않고 많은 실제 기계에 걸쳐 효율적일 가능성이 높다는 것이다.많은 문제에서, 최적의 캐시 불변 알고리즘은 세 개 이상의 메모리 계층 수준을 가진 기계에 최적일 것이다.^[4]null

예

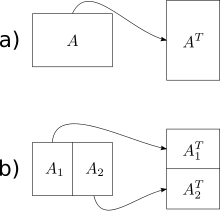
Frigo 외 연구진에서 제시된 가장 간단한 캐시 내성 알고리즘은 외부 매트릭스 전치 연산이다(전치 알고리즘도 전치용으로 고안되었지만, 비제곱 매트릭스의 경우 훨씬 더 복잡하다).m×n 어레이 A와 n×m 어레이 B를 고려하여, 우리는 A의 전치물을 B에 저장하고자 한다.순진한 해법은 한 배열을 큰 순서로, 또 다른 배열을 큰 순서로 가로지른다.열-주-주-주-주로 가로지른다.그 결과 행렬이 클 때 기둥-현행 횡단보도의 모든 단계에서 캐시 누락이 발생하게 된다.총 캐시 누락 수는 $\theta {\displaystyle \mathrm{}}$( ${\displaystyle m}$ n${\displaystyle }$) ${\displaystyle \Teta (mn)}$ 입니다$.$

캐쉬-관심 알고리즘은 최적의 작업 복잡성 $O{\displaystyle (m}$ n${\displaystyle }$) ${\displaystyle$ O$(mn)}$ 및$$ 최적의 캐시 복잡성 $O{\displaystyle (1+m}$ n${\displaystyle }$/ ${\displaystyle B)}$ ${\displaystyle O(1+mn/B)}$을 갖는다$.$기본 아이디어는 두 개의 큰 행렬의 전이를 작은 행렬(하위)의 전치물로 줄이는 것이다.우리는 행렬을 큰 차원을 따라 절반으로 나누어서 캐시에 들어갈 행렬의 전치 작업을 수행하면 된다.캐시 크기를 알고리즘에 알 수 없기 때문에 매트릭스는 이 지점 이후에도 계속 반복적으로 분할되지만, 이러한 추가 세분화는 캐시에 저장될 것이다.Once the dimensions m and n are small enough so an input array of size ${\displaystyle m\times n}$ and an output array of size ${\displaystyle n\times m}$ fit into the cache, both row-major and column-major traversals result in ${\displaystyle O(mn)}$ work and ${\displaystyle O(mn/B)}$헛수고이 분열과 정복 접근법을 사용함으로써 우리는 전체 행렬에 대해 동일한 수준의 복잡성을 달성할 수 있다.null

(원칙적으로 1×1 크기의 베이스 케이스에 도달할 때까지 매트릭스를 계속 나눌 수 있지만, 실제로는 재귀 서브루틴 호출의 오버헤드를 상각하기 위해 더 큰 베이스 케이스(예: 16×16)를 사용한다.)null

대부분의 캐시 취약 알고리즘은 분할 및 재무 접근법에 의존한다.그들은 캐시가 아무리 작더라도 결국 캐시에 들어맞도록 문제를 줄이고, 기능-호출 오버헤드 및 유사한 캐시 관련 최적화에 의해 결정된 어떤 작은 크기로 재귀성을 종료한 다음, 이 작고 해결된 문제의 결과를 병합하기 위해 어떤 캐시 효율적 액세스 패턴을 사용한다.null

외부 메모리 모델의 외부 정렬과 마찬가지로 캐시 구분도 병합과 닮은 깔때기와 퀵소트를 닮은 캐시 구분 분배의 두 가지 변형에서 가능하다.Like their external memory counterparts, both achieve a running time of ${\displaystyle O\left({\tfrac {N}{B}}\log _{\tfrac {M}{B}}{\tfrac {N}{B}}\right)}$, which matches a lower bound and is thus asymptotically optimal.^[6]null

실용성

우선 순위 대기열을 구현하는 2개의 RAM 기반 알고리즘, 1개의 캐시 인식 알고리즘 및 2개의 캐시 취약 알고리즘을 경험적으로 비교한 결과 다음과 같은 결과가 나왔다.^[7]

• 데이터가 메인 메모리에 적합할 때 캐쉬에 영향을 미치는 알고리즘이 RAM 기반 및 캐시 인식 알고리즘보다 더 나쁘게 수행됨
• 캐시 인식 알고리즘은 캐시 취약 알고리즘보다 구현이 훨씬 더 복잡해 보이지 않았으며, 연구에서 테스트한 모든 사례에서 최상의 성능을 제공했다.
• 캐쉬 망각 알고리즘은 데이터 크기가 메인 메모리 크기를 초과했을 때 RAM 기반 알고리즘을 능가했다.

또 다른 연구에서는 해시 테이블(RAM 기반 또는 캐시-유나웨어), B-tree(캐시 인식) 및 "벤더 세트"로 언급된 캐시 취약 데이터 구조를 비교했다.실행 시간과 메모리 사용량 모두 해시 테이블이 가장 좋았고, B-트리가 그 뒤를 이었으며, 벤더가 모든 경우에 최악을 설정했다.모든 테스트의 메모리 사용량은 메인 메모리를 초과하지 않았다.해시 테이블은 구현하기 쉬운 것으로 설명되었고, 벤더는 "올바른 구현을 위해 더 많은 노력이 필요했다"^[8]고 말했다.null

참고 항목

• 캐시 모호한 배포 정렬
• 외부 메모리 알고리즘
• 깔때기 소트

참조