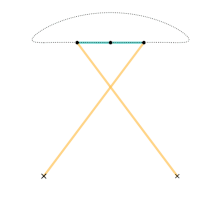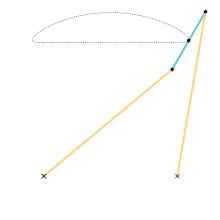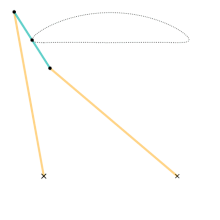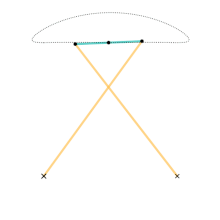
체비셰프 링크용 애니메이션입니다.치수:시안 링크 = a + a노란색 링크 = 5a접지 조인트 사이의 수평 거리 = 4a 체비셰프 연결은 회전 운동을 근사 선형 운동으로 변환하는 4개 막대 연결입니다.
그것은 운동학적 메커니즘의 이론적 문제를 연구한 19세기 수학자 파프누티 체비셰프에 의해 발명되었다.문제점 중 하나는 회전 운동을 대략적인 직선 운동으로 변환하는 링크의 구축이었다.이것은 제임스 와트가 증기 엔진을 [1]개량하면서 연구한 것이기도 하다.
운동 방정식
링크의 움직임은 속도, 힘 등을 통해 변경될 수 있는 입력 각도로 구속될 수 있습니다.입력 각도는 수평 링크2 L 또는 수평 링크4 L 중 하나입니다.입력 각도에 관계없이 A와3 B로 명명하는 링크L의 2개의 엔드 포인트와 중간 포인트의 움직임을 계산할 수 있습니다.


B 지점의 움직임이 다른 각도로 계산된다.


그리고 최종적으로 출력 각도를 입력 각도로 표기합니다.
![{\displaystyle \varphi _{2}=\arcsin \left[{\frac {L_{2}\,\sin(\varphi _{1})}{\overline {AO_{2}}}}\right]-\arccos \left({\frac {L_{4}^{2}+{\overline {AO_{2}}}^{2}-L_{3}^{2}}{2\,L_{4}\,{\overline {AO_{2}}}}}\right)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/755bcb0849486de8fc76bced42bcf8bed7d7e1ad)
이것에 의해, 상기의 2점과 중간점의 정의를 이용해, P점의 움직임을 쓸 수 있다.


입력 각도
두 경우 모두 입력 각도에 대한 한계는 다음과 같습니다.


사용.
체비셰프 링크는 증기 [citation needed]엔진에서 널리 사용되지 않았지만, 일반적으로 수평 러핑 크레인의 '호스 헤드' 설계로 사용됩니다.이 응용 프로그램에서는 대략적인 직선 이동이 선의 중간점에서 멀어지는 방향으로 변환되지만, 기본적으로는 동일한 메커니즘입니다.
「 」를 참조해 주세요.
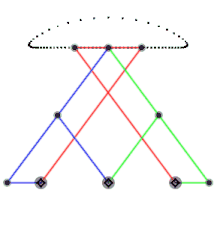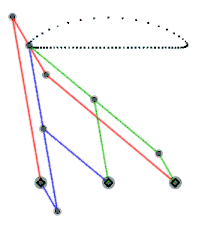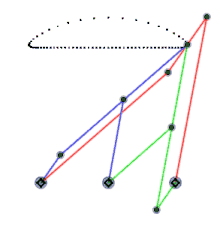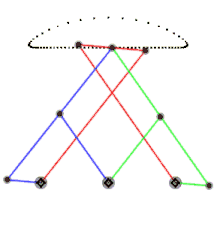
체비셰프의 람다 메커니즘(파란색과 녹색 각각 하나씩)은 동일한 운동 경로를 보여줍니다. 레퍼런스
외부 링크
Wikimedia Commons에는 체비셰프 링크와 관련된 미디어가 있습니다. 





![{\displaystyle \varphi _{2}=\arcsin \left[{\frac {L_{2}\,\sin(\varphi _{1})}{\overline {AO_{2}}}}\right]-\arccos \left({\frac {L_{4}^{2}+{\overline {AO_{2}}}^{2}-L_{3}^{2}}{2\,L_{4}\,{\overline {AO_{2}}}}}\right)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/755bcb0849486de8fc76bced42bcf8bed7d7e1ad)







