폐쇄형 시스템

폐쇄형 시스템은 물리, 화학 또는 공학 같은 다른 맥락에서 에너지의 전달이 허용되거나 허용되지 않지만 시스템 내부 또는 외부로 물질의 전달을 허용하지 않는 물리적 시스템이다.

물리학에서는

고전역학에서

비상대적 고전 역학에서 폐쇄적 시스템은 주변과 어떤 물질도 교환하지 않는 물리적 시스템이며, 그 근원이 시스템 외부에 있는 어떤 순력의 영향을 받지 않는다.^[1]^[2] 고전역학에서 폐쇄적인 시스템은 열역학에서 격리된 시스템과 동일할 것이다. 닫힌 시스템은 종종 특정한 문제나 실험의 결과에 영향을 미칠 수 있는 요인을 제한하기 위해 사용된다.

열역학에서

에너지 및 물질을 교환할 때 격리, 폐쇄 및 개방 시스템의 특성

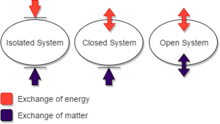
열역학에서, 폐쇄된 시스템은 주변 환경과 (열이나 작업으로) 에너지를 교환할 수 있지만 물질은 아니다. 고립된 시스템은 어떠한 열, 작업 또는 물질도 주변과 교환할 수 없는 반면, 개방된 시스템은 에너지와 물질을 교환할 수 있다.^[3]^[4]^[5]^[6]^[7]^[8]^[9] (이러한 용어의 정의 체계는 어떤 목적에는 편리하지만, 균일하게 쓰이지 않는다. 특히 여기서 '단절제'를 사용하는 '폐쇄제'를 쓰는 작가도 있다.)^[10]^[11]

입자(원자 또는 분자)의 한 종류만 있는 단순한 시스템의 경우, 닫힌 시스템은 입자의 수가 일정하게 된다. 그러나 화학반응을 겪고 있는 시스템의 경우 반응 과정에 의해 모든 종류의 분자가 생성되고 파괴될 수 있다. 이 경우, 어떤 종류의 분자라도 각 원소의 총수는 보존된다고 명시함으로써 시스템이 폐쇄된다는 사실을 나타낸다. 수학적으로:

\sum _{j=1}^{m}a_{ij}N_{j}=b_{i}}

여기서 $N_{j}$ $N_{j}$ ${\$ 는 $N_{j}$ j형 분자의 수, $a_{ij}$ $a_{ij}$ ${\$ $a_$ { $i$ $}는$ 분자 $a_{ij}$ $j$ ${\displaystyle$ j}에 있는 $i$ $i$ 의 수, b i ${\displaystyle b_$ ${i}}$ 는 $b_{i}$ $i$ $i$ 에서 원소의 총 원자 수, whing.ch는 시스템이 닫혀 있기 때문에 일정하게 유지된다. 시스템의 각 요소마다 그러한 방정식이 하나씩 있을 것이다.

열역학에서는 복잡한 열역학 문제를 해결하기 위해 폐쇄적인 시스템이 중요하다. 그것은 실험이나 문제의 결과를 변화시킬 수 있는 일부 외부 요인을 제거하여 이를 단순화할 수 있도록 한다. 열역학적 평형이 필요한 상황에도 폐쇄적인 시스템을 사용할 수 있다.

양자물리학에서

슈뢰딩거 방정식이라고 불리는 이 방정식은 고립되거나 폐쇄된 양자 시스템의 동작, 즉 정의에 의해 정보(즉 에너지 및/또는 물질)를 다른 시스템과 교환하지 않는 시스템이다. 따라서 분리된 시스템이 시간 t에서 어떤 순수 상태 ψ(t) ∈ H에 있는 경우, H는 시스템의 힐버트 공간을 나타내며,^[12] 이 상태의 시간 진화(두 번의 연속 측정 사이)가 된다.

i\hbar {\frac {\partial t}{\psi(\mathbf {r},t)={\hat {H}\psi(\mathbf {r},t)

여기서 어디는 허수 단위, ħ은 플랑크 2π을 나타내는 기호.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{으로 나눈 상수입니다.양자 s의 디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}∂/∂t 시간 t에 대한 일부 파생 상품,Ψ(는 그리스 문자 psi)는 파동 함수고 다른 형태톤에 따라 어떤 주어진 파동 함수의 총 에너지의 특징 Ystem, Ĥ은 해밀턴 연산자(그의 상황.

화학에서

화학에서, 닫힌 시스템은 반응제나 제품이 빠져나갈 수 없고, 열만 자유롭게 교환할 수 있는 것이다(예: 얼음 냉각기). 온도가 요인이 아닌 화학 실험을 수행할 때 폐쇄 시스템을 사용할 수 있다(즉, 열 평형에 도달하는 경우).

공학에서.

공학적인 맥락에서, 폐쇄형 시스템은 바운드 시스템이다. 즉, 모든 입력을 알 수 있고 모든 결과물을 특정 시간 내에 알 수 있다(또는 알 수 있다).

참고 항목

참조

^ Rana, N.C.; P.S. Joag (1991). Classical Mechanics. p. 78. ISBN 978-0-07-460315-4.
^ Landau, L.D.; E.M. Lifshitz (1976). Mechanics (third ed.). p. 8. ISBN 978-0-7506-2896-9.
^ Prigogine, I, Defay, R. (1950/1954) 화학 열역학, Longmans, Green & Co, London, 페이지 66.
^ 티사, L. (1966년) 일반화된 열역학, M.I.T 프레스, 캠브리지 MA, 페이지 112–113.
^ 구겐하임, E.A. (1949/1967) 열역학. 화학자와 물리학자를 위한 고급 치료, (제1판 1949), 제5판 1967, 노스홀랜드, 암스테르담, 페이지 14.
^ 뮌스터, A. (1970년) E.S.에서 번역한 고전 열역학 할버스타트, 와일리-인터사이언스, 런던, 6-7페이지.
^ 하세, R. (1971) 기초법률 조사, 열역학 제1장, 제1권 제1~97쪽, ed. 물리 화학의 W. Jost. 고급 논문, 에드. 에이링, D. Henderson, W. Jost, New York, Academic Press, lcn 73–117081, 페이지 3.
^ 노스웨스트의 쵸이글(2000년) 평형 및 안정 상태 열역학 기초, 암스테르담 엘스비에, ISBN 0-444-50426-5, 페이지 5.
^ 실비, R.J., 앨버티, R.A., 바웬디, M.G. (1955/2005) 물리 화학, 네 번째 판, 와일리, 호보켄 NJ, 페이지 4.
^ 캘런, H.B. (1960/1985) 열역학 및 서모스탯 소개, (1960년 1월호) 제2판 1985, 뉴욕 윌리, ISBN 0-471-86256-8, 페이지 17.
^ 테르 하르, D, 워즐랜드, H. (1966년) 열역학, 애디슨-웨슬리 출판, Reading MA, 페이지 43.
^ Rivas, Ángel; F. Huelga, Susana (October 2011). Open Quantum Systems. Berlin Heidelberg: Springer-Verlag. ISBN 978-3-642-23354-8.

[1] Rana, N.C.; P.S. Joag (1991). Classical Mechanics. p. 78. ISBN 978-0-07-460315-4.

[2] Landau, L.D.; E.M. Lifshitz (1976). Mechanics (third ed.). p. 8. ISBN 978-0-7506-2896-9.

[3] Prigogine, I, Defay, R. (1950/1954) 화학 열역학, Longmans, Green & Co, London, 페이지 66.

[4] 티사, L. (1966년) 일반화된 열역학, M.I.T 프레스, 캠브리지 MA, 페이지 112–113.

[5] 구겐하임, E.A. (1949/1967) 열역학. 화학자와 물리학자를 위한 고급 치료, (제1판 1949), 제5판 1967, 노스홀랜드, 암스테르담, 페이지 14.

[6] 뮌스터, A. (1970년) E.S.에서 번역한 고전 열역학 할버스타트, 와일리-인터사이언스, 런던, 6-7페이지.

[7] 하세, R. (1971) 기초법률 조사, 열역학 제1장, 제1권 제1~97쪽, ed. 물리 화학의 W. Jost. 고급 논문, 에드. 에이링, D. Henderson, W. Jost, New York, Academic Press, lcn 73–117081, 페이지 3.

[8] 노스웨스트의 쵸이글(2000년) 평형 및 안정 상태 열역학 기초, 암스테르담 엘스비에, ISBN 0-444-50426-5, 페이지 5.

[9] 실비, R.J., 앨버티, R.A., 바웬디, M.G. (1955/2005) 물리 화학, 네 번째 판, 와일리, 호보켄 NJ, 페이지 4.

[10] 캘런, H.B. (1960/1985) 열역학 및 서모스탯 소개, (1960년 1월호) 제2판 1985, 뉴욕 윌리, ISBN 0-471-86256-8, 페이지 17.

[11] 테르 하르, D, 워즐랜드, H. (1966년) 열역학, 애디슨-웨슬리 출판, Reading MA, 페이지 43.

[12] Rivas, Ángel; F. Huelga, Susana (October 2011). Open Quantum Systems. Berlin Heidelberg: Springer-Verlag. ISBN 978-3-642-23354-8.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

Search