Cost curve

In economics, a cost curve is a graph of the costs of production as a function of total quantity produced. In a free market economy, productively efficient firms optimize their production process by minimizing cost consistent with each possible level of production, and the result is a cost curve. Profit-maximizing firms use cost curves to decide output quantities. There are various types of cost curves, all related to each other, including total and average cost curves; marginal ("for each additional unit") cost curves, which are equal to the differential of the total cost curves; and variable cost curves. Some are applicable to the short run, others to the long run.

Notation

There are standard acronyms for each cost concept, expressed in terms of the following descriptors:

• SR = short-run (when the amount of physical capital cannot be adjusted)
• LR = long-run (when all input amounts can be adjusted)
• A = average (per unit of output)
• M = marginal (for an additional unit of output)
• F = fixed (unadjustable)
• V = variable (adjustable)
• T = total (fixed plus variable)

• C = cost

These can be combined in various ways to express different cost concepts (with SR and LR often omitted when the context is clear): one from the first group (SR or LR); none or one from the second group (A, M, or none (meaning “level”); none or one from the third group (F, V, or T); and the fourth item (C).

다양한 조합에서 다음과 같은 단기 비용 곡선을 볼 수 있다.

• 단기평균고정비용(SRAFC)
• 단기평균총원가(SRAC 또는 SRATC)
• 단기평균변수비용(AVC 또는 SRAVC)

• 단기 한계비용(SRMC)
• 단기 고정 비용(FC 또는 SRFC)
• 단기총원가(SRTC)
• 단기 가변 비용(VC 또는 SRVC)

및 다음과 같은 장기 비용 곡선:

• 장기평균총원가(LRAC 또는 LRATC)
• 장기적 한계비용(LRMC)
• 장기총비용(LRTC)

단기 총비용(SRTC) 및 장기 총비용(LRTC) 곡선

단기 총비용(SRTC)과 장기 총비용(LRTC) 곡선은 생산량이 증가하고 있다. 왜냐하면 더 많은 생산량을 생산하려면 장단기적으로 더 많은 노동력을 사용해야 하기 때문이다. 그리고 장기적으로 더 많은 생산량을 생산하려면 더 많은 물리적 자본 투입을 사용해야 하기 때문이다. 그리고 두 입력 중 더 많은 것을 사용해야 하기 때문이다. 투입 비용 증가

단기적으로 하나의 가변 투입물(노동력 사용량)만 있으면, 각각의 가능한 생산량에는 특정한 노동력 사용량이 필요하며, 생산 수준의 함수로서 단기 총비용은 노동력의 단가를 곱한 이 독특한 노동력의 양이다. 그러나 장기적으로는 노동 자본과 물리적 자본의 수량을 모두 선택할 수 있는 상황에서 특정 생산 수준의 생산에 드는 총 비용은 최적화 문제의 결과물이다. 노동에 대한 지출의 합계(임금률이 노동 사용량의 선택된 수준을 곱함)와 자본에 대한 지출(자본 단가, 물리적 자본 사용의 선택된 수준을 곱함)은 노동 사용과 자본 사용에 관하여 최소화되며, 두 입력 사용량에 대한 산출물과 관련된 생산 기능 균등에 따라 결정된다.l) 총비용의 수준은 주어진 생산량을 생산하는 총비용이다.

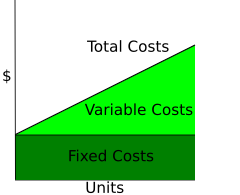
단기 실행 변수 및 고정 비용 곡선(SRVC 및 SRFC 또는 VC 및 FC)

단기 고정 비용(FC/SRFC)은 출력 수준에 따라 달라지지 않기 때문에 여기에 표시된 것처럼 곡선이 수평이다. 출력 수준이 높아질수록 단기 가변 비용(VC/SRVC)은 증가하는데, 생산량이 많을수록 가변 입력물을 더 많이 사용하고 비용을 지불해야 하기 때문이다.

단기 평균 가변 비용 곡선(AVC 또는 SRAVC)

평균 가변 비용(AVC/SRAVC) (단기 개념)은 출력 단위당 가변 비용(일반적으로 노동 비용)이다. SRAVC = wL/Q 여기서 w는 임금률, L은 사용 노동력의 양, Q는 산출물의 양이다. SRAVC 곡선은 출력 수준에 대한 단기 평균 변수 비용을 나타내며 일반적으로 U자형으로 그려진다. 그러나 이것이 경제이론에는 편리하지만 현실 세계와는 거의 관계가 없다는 주장이 제기되어 왔다. 일부 추정치는 적어도 제조업의 경우 U자형 비용 곡선을 보고하는 기업의 비율이 5~11%에 이른다는 것을 보여준다.^[1][2]

단기평균고정비용곡선(SRAFC)

정의에 따른 고정비는 출력에 따라 달라지지 않기 때문에 출력이 높을 때 단기 평균 고정비(SRAFC) 즉, 출력 단위당 단기 고정비)가 낮아져 표시된 하향곡선이 발생한다.

단기 및 장기 평균 총 비용 곡선(SRATC 또는 SRAC 및 LRATC 또는 LRAC)

평균 총비용 곡선은 출력 단위당 비용과 출력 수준, 즉 ceteris paribus 사이의 관계를 포착하기 위해 구성된다. 완벽히 경쟁적이고 생산적으로 효율적인 기업은 생산요소의 사용이 생산될 생산량의 주어진 수준에 따라 가능한 한 낮게 생산요소를 구성한다. 단기적으로는 최소한 한 가지 생산 요인이 고정되어 있을 때, 이는 생산량 증가에 따른 가능한 모든 평균 비용 이득을 누려온 생산량 수준에서 발생한다. 이것은 위 도표의 최소 지점에 있다.

단기 총비용 제공자:

${\displaystyle S}$ ${\displaystyle T}$ ${\displaystyle C}$= ${\displaystyle P}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ K${\displaystyle }$+ ${\displaystyle {}_{}}$ ${\displaystyle L}$ ${\displaystyle {}_{}}$ L ${\displaystyle STC=P_{K}\cdot K+P_{L}\cdot$ L$}$,

여기서 P는_K 단위시간당 물리적 자본을 사용하는 단가, P는_L 단위시간당 노동력의 단가(임금율), K는 물리적 자본의 사용량, L은 노동력의 사용량이다. 이를 통해 SATC 또는 SRAC로 표시된 단기 평균 비용을 STC/Q:

${\displaystyle SRATC\ or\ SRAC={\frac {P_{K}\cdot K}{Q}}+{\frac {P_{L}\cdot L}{Q}}={\frac {P_{K}\cdot P_{K}}{A}}+{\frac {P_{L}\cdot P_{L}}{A}}}$,

where ${\textstyle AP_{K}={\frac {Q}{K}}}$ is the average product of capital and ${\textstyle AP_{L}={\frac {Q}{L}}}$ is the average product of labor.^{[3]: 191}

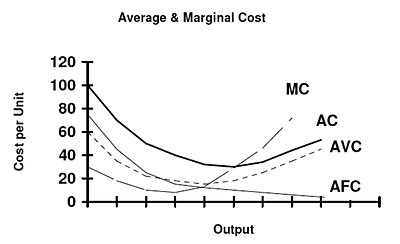
Within the graph above, the Average Fixed Cost curve and Average Variable Cost curve cannot start with zero, as at quantity zero these values are not defined since they would involve dividing by zero.

Short-run average cost (SRATC/SRAC) equals average fixed costs plus average variable costs. Average fixed cost continuously falls as production increases in the short run, because K is fixed in the short run. The shape of the average variable cost curve is directly determined by increasing and then diminishing marginal returns to the variable input (conventionally labor).^{[4]: 210}

The long-run average cost (LRATC/LRAC) curve looks similar to the short-run curve, but it allows the usage of physical capital to vary.

Short-run marginal cost curve (SRMC)

A short-run marginal cost (SRMC) curve graphically represents the relation between marginal (i.e., incremental) cost incurred by a firm in the short-run production of a good or service and the quantity of output produced. This curve is constructed to capture the relation between marginal cost and the level of output, holding other variables, like technology and resource prices, constant. The marginal cost curve is usually U-shaped. Marginal cost is relatively high at small quantities of output; then as production increases, marginal cost declines, reaches a minimum value, then rises. The marginal cost is shown in relation to marginal revenue (MR), the incremental amount of sales revenue that an additional unit of the product or service will bring to the firm. This shape of the marginal cost curve is directly attributable to increasing, then decreasing marginal returns (and the law of diminishing marginal returns). Marginal cost equals w/MP_L.^{[3]: 191} For most production processes the marginal product of labor initially rises, reaches a maximum value and then continuously falls as production increases. Thus marginal cost initially falls, reaches a minimum value and then increases.^{[4]: 209} The marginal cost curve intersects both the average variable cost curve and (short-run) average total cost curve at their minimum points. When the marginal cost curve is above an average cost curve the average curve is rising. When the marginal costs curve is below an average curve the average curve is falling. This relation holds regardless of whether the marginal curve is rising or falling.^{[5]: 226}

장기적 한계비용곡선(LRMC)

장기적 한계비용(LRMC) 곡선은 장기적 생산에서 발생하는 총비용, 즉 모든 생산요소가 변동하는 개념적 기간을 각 생산단위에 대해 보여준다. 달리 말하면, LRMC는 모든 투입변수가 가변적일 때 하나의 생산단위의 증가와 관련된 총비용의 최소증가액이다.^[6]

장기적 한계비용 곡선은 단기적 개념인 한계수익 감소 법칙보다는 장기적 개념인 규모적 수익률에 의해 형성된다. 장기적 한계비용 곡선은 투입 유연성이 높아져 단기적 대비에 비해 평탄한 경향이 있다. 롱런 한계비용 곡선은 롱런 평균비용 곡선과 후자의 최소 지점에서 교차한다.^{[3]: 208} 장기간의 한계원가가 장기간의 평균원가 이하일 경우 장기간의 평균원가는 하락하고 있다(추가적인 산출단위를 고려함에 따라).^{[3]: 207} 장기간의 한계원가가 장기간의 평균원가보다 높을 때, 평균원가는 상승하고 있다. 장기간의 한계비용은 최소-평균-최소-장기간의 한계비용 수준에서의 단기간의 한계비용은 단기간의 한계비용과 같다. LRMC는 LR 총비용 함수의 기울기다.

수익 곡선과 함께 비용 곡선 그래프 작성

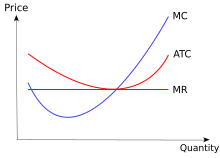
비용 곡선은 기업에 대한 정보를 제공하기 위해 결합될 수 있다. 예를 들어, 이 다이어그램에서 기업들은 완벽하게 경쟁적인 시장에 있다고 가정한다. 완벽하게 경쟁적인 시장에서 장기적으로 기업들이 직면하게 되는 가격은 한계비용 곡선이 평균비용 곡선을 줄이는 가격일 것이다. 왜냐하면 어떤 가격보다 높거나 낮으면 산업으로 진입하거나 퇴장하여 시장에서 결정된 가격을 경제적 이익 제로 수준으로 끌어올리기 때문이다.

비용 곡선 및 생산 기능

인자 가격이 일정하다고 가정하면 생산함수는 모든 원가 함수를 결정한다.^[4] 가변원가곡선은 반전된 단기생산함수 또는 총생산곡선의 변동입력 곱에 대한 일정한 가격이며, 그 행태와 성질은 생산함수에 의해 결정된다.^{[3]: 209 [nb 1]} 생산함수는 가변원가함수를 결정하기 때문에 한계원가곡선의 형태와 특성, 평균원가곡선의 형태를 반드시 결정한다.^[4]

만약 기업이 모든 투입 시장에서 완벽한 경쟁자이고 따라서 모든 투입변수의 단위 가격은 기업이 얼마나 많은 투입변수를 구매하느냐에 영향을 받지 않는다면, 기업은 특정한 생산수준에서 규모의 경제(즉, 장기 평균비용 곡선의 하향경사 지역에서 영업 중)를 가지고 있음을 보여줄 수 있다.규모에 맞는 수익률이 증가하는 경우.^[7][8][9] 마찬가지로 규모에 대한 수익률이 감소하는 경우에만 규모의 비경제적(장기 평균 비용 곡선의 상승 기울어진 지역에서 운용되고 있음)을 가지고 있으며, 규모에 대한 수익이 일정하다면 규모의 경제도, 비경제적도 없다. 이 경우, 생산 시장에서의 완벽한 경쟁과 함께 장기간의 시장 균형은 장기간의 평균 비용 곡선의 최소 지점(즉 규모의 경제와 불경제 사이의 경계선)에서 운영되는 모든 기업을 포함할 것이다.

그러나 만약 기업이 투입 시장에서 완벽한 경쟁자가 아니라면, 위의 결론은 수정된다. 예를 들어, 어떤 범위의 출력 수준에서 규모 확대에 대한 수익률이 증가하지만, 기업이 하나 이상의 입력 시장에서 너무 커서 입력물 구매를 증가시키면 입력물의 단위 비용을 증가시킬 수 있다면, 기업은 그 범위의 출력 수준에서 규모의 불경제성을 가질 수 있다. 반면에, 만약 기업이 입력의 대량 할인을 받을 수 있다면, 그 출력 범위에서 생산 수익률이 감소하더라도 일정 범위의 출력 수준에서 규모의 경제를 가질 수 있다.

서로 다른 곡선 간의 관계

• 총 비용 = 고정 비용(FC) + 가변 비용(VC) = 평균 총 비용(ATC) x 수량(Q)
• 한계비용(MC) = dC/dQ; MC는 총비용함수와 가변비용함수의 기울기와 같다.
• 평균 총 비용(ATC) = 총 비용/Q
• 평균 고정 비용(AFC) = FC/Q
• 평균 가변 비용(AVC) = VC/Q.
• ATC = AFC + AVC
  • MC 곡선이 평균 총비용 또는 평균 가변비용 곡선을 초과하는 Q 수준에서 후자 곡선은 상승하고 있다.^{[10]: 212}
  • MC가 평균 총비용이나 평균 가변비용 이하라면 후자 곡선이 하락하는 것이다.
  • 만약 MC가 평균 총비용과 같다면, 평균 총비용은 최소값이다.
  • MC가 평균 가변비용과 같다면, 평균 가변비용은 최소값이다.

단기 비용과 장기 비용 곡선 간의 관계

각 산출물 수량에 대해 하나의 비용-최소화 자본 수준과 주어진 수량 생산과 관련된 고유한 단기 평균 비용 곡선이 있다.^[11] 다음의 진술은 기업이 생산된 수량에 대해 최적의 자본 수준을 사용하고 있다고 가정한다. 만약 그렇지 않다면, SRAC 곡선은 LRAC의 "무릎 위에" 놓여 있고 어느 지점에서 접선되지 않을 것이다.

• 각 STC 곡선은 한 점에서만 LRTC 곡선과 접할 수 있다. STC 곡선은 LRTC 곡선을 교차(절편)할 수 없다.^{[4]: 230 [10]: 228–229} STC 곡선은 접선점이 없는 LRTC 곡선의 전체 "위"에 놓일 수 있다.^{[12]: 256}
• 하나의 STC 곡선은 장기적 원가-최소 생산 수준에서 LRTC에 접한다. 접선 지점에서 LRTC = STC. 다른 모든 생산 수준에서 STC는 LRTC를 초과할 것이다.^{[13]: 292–299}
• 평균 비용 함수는 총 비용 함수를 출력 수준으로 나눈 값이다. 따라서 SATC 곡선은 또한 출력의 비용 최소화 수준에서 LRATC 곡선과 접선된다. 접선 지점에서 LRATC = SATC. 다른 모든 수준의 생산 SATC > LRATC^{[13]: 292–299} 기업은 접선 지점의 왼쪽에서 너무 많은 자본을 사용하고 있으며 고정 비용이 너무 높다. 접선 지점의 오른쪽에서 그 회사는 자본을 너무 적게 사용하고 있고 노동에 대한 수익의 감소는 비용 증가를 야기하고 있다.^[14]
• 총 비용 곡선의 경사는 한계 비용과 동일하다. 따라서 STC가 LTC에 접하면 SMC = LRMC가 된다.
• 장기 실행 비용 최소화 수준의 출력 LRTC = STC, LRATC = SATC 및 LRMC = SMC,^{[13]: 292–299}
• 장기 실행 비용 최소화 생산 수준은 최소 SATC와 다를 수 있다.^{[10]: 229 [15]: 186}
• 입력 단가가 고정되어 있는 경우, 생산 함수의 스케일이 일정하게 증가한다면, SATC 곡선의 최소 수준에서 SATC = LRATC = SMC = LRMC가 있다.^{[13]: 292–299}
• 입력 단가가 고정되어 있는 상태에서 생산함수가 스케일로 리턴을 증가시키는 경우, SATC 곡선의 최소값은 LRAC와 SATC 곡선 사이의 접선점 오른쪽에 있다.^{[13]: 292–299} 여기서 LRTC = STC, LRTC = SATC, LRMC = SMC.
• 입력 단가가 고정되고 수익률이 감소하면 SATC 곡선의 최소값은 LRAC와 SATC 사이의 접선 지점의 왼쪽에 있다.^{[13]: 292–299} 여기서 LRTC = STC, LRATC = SATC, LRMC = SMC.
• 고정단위의 투입원가를 가지고, 증가(감소)의 회수를 경험하고 있는 기업이, 최소의 SAC로 생산하고 있는 기업은, 고정 투입물의 이용을 확대(감소)함으로써, 항상 장기적으로는 평균비용을 절감할 수 있다.^{[13]: 292–99 [15]: 186}
• LRATC는 항상 SATC와 같거나 그보다 작다.^{[3]: 211}
• 생산 공정에서 규모에 대한 지속적인 수익률을 보일 경우 최소 SRAC는 최소 장기 평균 비용과 동일하다. LRAC와 SRAC는 공통 최소값으로 교차한다. 따라서 SRMC = LRMC = LRAC = SRAC를 확장하기 위한 지속적인 수익률.
• 생산 공정에서 감소 또는 증가를 경험하는 경우 최소 단기 평균 비용은 최소 장기 평균 비용과 같지 않다. 규모에 대한 증가수익이 존재하는 경우 최소 주행은 SRAC보다 낮은 출력 수준에서 발생한다. 이는 이용되지 않은 규모의 경제가 있기 때문에 장기적으로 기업은 항상 더 큰 공장을 사용함으로써 최소 단기 평균 비용보다 낮은 가격으로 수량을 생산할 수 있기 때문이다.^[16]
• 수익률이 감소함에 따라, 최소 SRAC는 최소 LRAC보다 낮은 생산 수준에서 발생한다. 왜냐하면 기업은 단순히 크기나 운영을 줄임으로써 평균 비용을 줄일 수 있기 때문이다.
• SRAC의 최소값은 경사가 0일 때 발생한다.^[17] 따라서 U자형 LRAC 곡선과 SRAC 곡선의 최소값 사이의 접선점은 규모의 경제를 지속적으로 보여주는 LRAC 곡선의 해당 부분과 일치할 것이다. LRAC와 SRAC 사이의 접선 지점을 확대하기 위해서는 SRAC 곡선의 최소값과 관련된 수준 이하의 출력 수준에서 발생해야 한다.

U자형 곡선

SRAC와 LRAC 곡선은 모두 일반적으로 U자형으로 표현된다.^{[10]: 211, 226 [15]: 182, 187–188} 그러나 곡선의 모양은 같은 요인 때문은 아니다. 단기 주행 곡선의 경우 초기 하향 경사는 주로 평균 고정 비용의 감소에 기인한다.^{[4]: 227} 낮은 생산 수준에서 가변 입력에 대한 수익률 증가도 한몫하는 반면,^[18] 상승 기울기는 가변 입력에 대한 한계 수익 감소에 기인한다.^{[4]: 227} 장기간의 곡선에서는 정의에 의한 형태는 규모의 경제와 불경제를 반영한다.^{[15]: 186} 생산 장기적 생산 함수의 낮은 수준에서 일반적으로 입력 시장의 완벽한 경쟁자들 기업들을 위해 장기적 평균 비용이 떨어지고 있는 방법으로요. 결과가[4]:출력의 더 높은 수준에서 장기적 평균 비용 함수의 227을 상향하는 경사가 증가하며 수익에서 축소하기 위해 감소할 예정이다. 그ou티푸트 ^{[4]: 227} 레벨

평균 비용 곡선의 경험적 형태

평균 비용 곡선이 일반적으로 U자형이 아님을 보여주는 증거가 있다. Wilford J. Eiteman과 Glen E의 조사에서. 1952년 334개 회사의 관리자들은 여러 가지 다른 비용 곡선을 보여주었고, 어떤 것이 회사의 비용 곡선을 가장 잘 나타내는지 명시해 달라고 요청했다. 조사에 응답한 관리자의 95%가 지속적인 비용 또는 감소 비용으로 비용 곡선을 보고하였다.^[1]

앨런 블라인더 전 미국경제학회 부회장은 1998년 미국 경제 전반을 대표해야 할 표본에 200개 미국 기업이 참여한 같은 유형의 조사를 했다. 그는 기업의 약 40%가 변동원가 또는 한계원가 하락을 보고했고, 48.4%는 변동원가/변동원가 하락을 보고했다는 것을 발견했다.^[19]

참고 항목

메모들

참조