쿠엣 흐름

유체 역학에서 쿠엣 흐름은 두 표면 사이의 공간에 있는 점성 유체의 흐름이며, 그 중 하나는 다른 표면과 비교하여 접선적으로 움직인다. 표면의 상대적인 움직임은 유체에 전단 응력을 가하고 유동을 유도한다. 용어의 정의에 따라 흐름 방향에 적용된 압력 구배가 있을 수도 있다.

쿠엣 구성은 지구의 맨틀과 대기와 같은 특정한 실제적인 문제를 모델링하며 가벼운 하중으로 저널 베어링을 흐른다.^[1] 또한 점도계에 사용되며 가역성의 근사치를 나타낸다.^[2][3]

19세기 말 프랑스 앵거스 대학의 물리학과 교수인 모리스 쿠엣의 이름을 따서 지어졌다.

플라나르 쿠에트 흐름

쿠엣 흐름은 전단 구동 유체 운동을 설명하기 위해 학부 물리학과 공학 과정에서 자주 사용된다. 단순한 구성은 거리 $h{\displaystyle }$ ${\displaystyle h}$로 분리된 두 개의 무한 평행 판에 해당한다$.$ 하나의 판은 자신의 평면에서$$ 일정한 상대 $속도{\displaystyle }$ U ${\displaystyle U}$로 번역된다. 압력 그라데이션 무시, Navier–스토크 방정식은 다음과 같이 단순화된다.

${\displaystyle {\frac {d^{2}u}{dy^{2}}=0,}$

여기서 $y{\displaystyle }$ ${\displaystyle y}$은 플레이트에 정규적인 공간 좌표고 ${\displaystyle u}$(${\displaystyle }$) ${\displaystyle u(y)}$은 속도 필드다. 이 방정식은 흐름이 단방향이라는 가정을 반영한다. 즉$,$ 세 가지 속도 성분$({\displaystyle u}$ , v${\displaystyle }$, ${\displaystyle w}$ )${\displaystyle }$중 하나만 $비삼각형(u,v,w)$이다. 하단 플레이트가 $y{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle y=0$에 해당하는 경우 경계조건은${\displaystyle }u{\displaystyle }$ (${\displaystyle 0}$) = ${\displaystyle 0}${\$displaystyle u(0)=0$$}$ 및${\displaystyle }u{\displaystyle }$ (${\displaystyle h}$) = ${\displaystyle U}${\$displaysty u(h)=$이다.$U}$ $.$ 정확한 해결책

$u(y)=U{\frac{y}{h}}$

두 번 통합하고 경계 조건을 사용한 상수에 대한 해결로 찾을 수 있다. 흐름의 주목할 만한 측면은 전단 응력이 영역 전체에 걸쳐 일정하다는 것이다. 특히 속도의 첫 번째 파생상품인 $U{\displaystyle /h}$ ${\displaystyle U/h$은 일정하다. 뉴턴의 점도의 법칙(뉴턴 액)에 따르면 전단 응력은 이 표현과 (정수) 유체 점도의 산물이다.

시작

현실적으로 쿠엣 해법은 순간적으로 도달하지 못한다. 안정 상태에 대한 접근법을 설명하는 "시동 문제"는 다음에서 제시한다.

${\displaystyle {\frac {\fract t}}{\preason t}=\nu {\fract {\preason ^{2}u}{\preased y^{2}}:$

초기의 조건에 따라.

${\displaystyle u(y,0)=0,\pair 0(h)}$

그리고 일정한 흐름과 동일한 경계 조건의 경우:

${\displaystyle u(0,t)=0,\quad u(h,t)=U,\quad t>0.}$

그 문제는 일정한 용액을 빼서 균일하게 만들 수 있다. 그런 다음 변수 분리를 적용하면 다음과 같은 해결책이 나온다.^[4]

${\$$U{\frac {y}{h}-{\frac {2$$}$$U}{\pi }{\pi }\$sum _${n=1$}^{n1$}{n1}e^{$n1$}{n^{2$}\pi$^{2}{\frac {\nu$ t$}{h^{2}}:}\sin \left[n-{y}}}{h}}}}}}오른쪽$

안정 상태에 대한 이완을 설명하는 시간 척도는 그림에서와 같이 $t{\displaystyle }$~ h ${\displaystyle {2\mathrm{}}^{}}$/ ${\displaystyle \nu }$ ${\displaystyle t\sim h^{2}/\nu }$이다$.$ 안정 상태에 도달하는 데 필요한 시간은 플레이트 $h{\displaystyle }$ ${\displaystyle h}$과 유체의 동적 점성 사이의 간격에 따라 달라지지만 $U{\displaystyle }$ ${\displaystyle U}$에는 그렇지 않다$.$

압력 경사도가 있는 평면 흐름

보다 일반적인 쿠엣 흐름은 평판에 평행한 방향으로 ${\displaystyle \mathrm{일정}}$한 압력 $그라데이션{\displaystyle }$ G${\displaystyle }$=${\displaystyle }$- d${\displaystyle p}$ /${\displaystyle d}$ ${\displaystyle x\mathrm{}}$ = ${\displaystyle \mathrm{c}}$ ${\displaystyle \mathrm{o}}$ ${\displaystyle \mathrm{n}}$ ${\displaystyle \mathrm{s}}$ t ${\$을(를) 포함한다. 더 나비에–스토크 방정식은

${\daystyle {\frac {d^{2}u}{dy^{2}}=-{\frac {G}{\mu }}},}$

여기서 $[\displaystyle \mu }$은(는) 동적 점성이다. 위의 방정식을 두 번 통합하고 경계 조건(압력 구배가 없는 쿠엣 흐름의 경우와 동일)을 적용하면 다음과 같은 결과를 얻을 수 있다.

${\displaystyle u(y)={\frac {G}{2\mu }}}y\,(h-y)++U{\frac {y}{h}}.}$

압력 구배는 양수(부압 구배) 또는 음수(우호 압력 구배)일 수 있다. 정지판의 제한 사례(${\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle U=0}$ )에서 $$유량을 평면 푸아세유 흐름이라고 하며, 대칭(수평 중간 평면) 포물선 속도 프로파일을 참조한다.^[5]

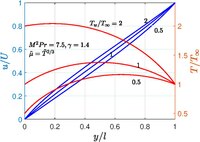
압축유동

압축 불가능한 흐름에서는 유체 온도가 일정하기 때문에 속도 프로파일이 선형이다. 상·하벽이 서로 다른 온도에서 유지될 때 속도 프로파일이 더 복잡해진다. 그러나 1950년 C. R. 일링워스에서 보듯이 정확한 암묵적 해결책을 가지고 있다.^[6]

정지 상태에서 하부 벽이 있는 Couette 흐름과 등속 $U{\displaystyle }${\$displaystyle U}$을(를) 사용하여 상단 벽이 움직이는 평면 Couette 흐름을 고려하십시오$.$ 하단 $벽$의 유체$특성$은 첨자 w {\displaystyle $w},$ 상단 벽의 특성은$$ 첨자 $\infty {\displaystyle \mathrm{}}$ ${\displaystyle \inft$ 속성과 압력. 벽은 기준 수량으로 규정되고 취해진다. $l{\displaystyle }$ ${\displaystyle l}$을(를) 두 벽 사이의 거리로$$ 두십시오. 경계조건은

${\displaystyle u=0,\ v=0,\ h=h_{w}=c_{pw}T_{w}\{\text{at}\y=0,}$

${\displaystyle u=U,\ v=0,\h_{\\infit }=c_{p\infit }{\infit }\p=p_{\infit }\p=p_{\infit}\{\text{at}\}\y=l}$

여기서 $h{\displaystyle }$ ${\displaystyle h}$은(는) 특정 엔탈피이고 $c{\displaystyle {}_{}}$ ${\displaystyle p_{}}$ ${\$는 특정 열이다. 질량 및 $y{\displaystyle }$ ${\displaystyle y}$ -momentum을$$ 보존하려면 흐름 영역 어디에나$$ $v{\displaystyle }$= 0${\displaystyle ,}$ ${\displaystyle \text{p}}$= p$$ {\$displaystyle v=0,\p=p_{\ft}}}$가 필요하다. 에너지 절약 및 $x{\displaystyle }$ ${\displaystyle x}$ -모멘텀$$ 감소

${\displaystyle {\frac {d}{did}}\왼쪽(\mu {\frac {du}{dy}\오른쪽)=0,\quad \rightarrow \quad \frac {d\d\tau}}}=0,\quad \rigarrow \quau =\{w}$

${\displaystyle {\frac {1}{\mathrm {Pr}}}}}}{dy}}\좌(\mu {\frac {dh}{dy}}\우)+\mu \좌({\frac {du}{dy}}\우)^{2}=0.}$

여기서 $\tau {\displaystyle }$= ${\displaystyle {}_{}}$ ${\displaystyle w_{}}$= ${\displaystyle \text{상수}}$ ${\$는 벽 전단 응력이다. The flow does not depend on the Reynolds number ${\displaystyle \mathrm {Re} =Ul/\nu _{\infty }}$, but rather on the Prandtl number ${\displaystyle \mathrm {Pr} =\mu _{\infty }c_{p\infty }/\kappa _{\infty }}$ and the Mach number ${\displaystyle \mathrm{M}=U/c_{\mathrm{\infty }}=U/\sqrt{(\gamma -1)h_{}}}$$∞{\$ $\$$mathrm{M} =U/c_{\infit }=U/{\sqrt{(\gamma -1)h_{\$$infit$ $\}\}\}\}\},$ 여기서 ${\displaystystyle c}$는 음속의 속도, $\gamma$ ${\displaystytype \gamma.$ 비차원 변수 소개

$displaystyle {\y}={\frac}}}{\frac {l}},\quad {\tilde{\}}}}}T}={\frac {T}{\frac}}{\frac}}{{\frac}}}{{{pT_{\infty }}},\quad {\tilde {T}}_{w}={\frac {T_{w}}{T_{\infty }}},\quad {\tilde {h}}={\frac {h}{h_{\infty }}},\quad {\tilde {h}}_{w}={\frac {h_{w}}{h_{\infty }}},\quad {\tilde {u}}={\frac {u}{U},\quad {\tilde{\mu }}={\frac {\mu }{\mu }{\mu }},\quad {\tilde {\\tau }}}={\frac {\w}{\mu }{\fl}}}}}}}}}}}}}$

이러한 수량으로 볼 때 해결책은

${\displaystyle {\tilde {h}}={\tilde {h}}_{w}+\left[{\frac {\gamma -1}{2}}\mathrm {M} ^{2}\mathrm {Pr} +(1-{\tilde {h}}_{w})\right]{\tilde {u}-{{\frac {\gamma -1}{2}}\mathrm {M}^{2}\mathrm {Pr} \,{\tilde {u}^{2},}$

${\displaystyle {\tilde {y}}={\frac {1}{{\tilde {\tau }}_{w}}}\int _{0}^{\tilde {u}}{\tilde {\mu }}d{\tilde {u}},\quad {\tilde {\tau }}_{w}=\int _{0}^{1}{\tilde {\mu }}d{\tilde {u}},\quad q_{w}=-{\frac {1}{\mathrm {Pr} }}\tau _{w}\left({\frac {dh}{du}}\right)_{w},}$

여기서 $q{\displaystyle {}_{}}$ ${\displaystyle w_{}}$ ${\$는 하부 벽에서 단위 면적당 단위 시간 당 전달되는 열이다$$. Thus ${\displaystyle {\tilde {h}},{\tilde {T}},{\tilde {u}},{\tilde {\mu }}}$ are implicit functions of ${\displaystyle y}$. One can also write the solution in terms of the recovery temperature ${\displaystyle T_{r}}$ and recovery enthalpy ${\displaystyle h_{r}}$$$ 절연벽의 온도에서 평가됨. 즉$$, ${\displaystyle q_{}}$= ${\displaystyle 0}$ ${\displaystyle$ $T_{w}}$ 및 $h$ ${\displaystyle {값}_{}}$ ${\$ $h_{w$^{[clarification needed]} 그렇다면 해결책은

$w}{w}{ww}}{w}}{\ {q_{w}}{\tau_{w}}}U}}={\frac {{\tilde {T}}_{w}-{\tilde {T}}_{r}}{(\gamma -1)\mathrm {M} ^{2}\mathrm {Pr} }},\quad {\tilde {T}}_{r}=1+{\frac {\gamma -1}{2}}\mathrm {M} ^{2}\mathrm {Pr} ,}$

${\displaystyle {\tilde {h}}={\tilde {h}}_{w}+({\tilde {h}}_{r}-{\tilde {h}}_{w}){\tilde {u}}-{\frac {\gamma -1}{2}}\mathrm {M} ^{2}\mathrm {Pr} \,{\tilde {u}}^{2}.}$

특정 열이 일정하면 $h{\displaystyle \mathrm{}}$${\displaystyle \stackrel{}{}}$~${\displaystyle }$= ${\displaystyle T\stackrel{}{}}$~ ${\$ ${\displaystyle \mathrm{M}}$→ 0 ${\displaystyle \mathrm {M} \rightarrow$ 0$}$ $및$ ${\displaystyle T_{}}$= ${\displaystyle {}_{}}$ =${\displaystyle q_{}\mathrm{q}}$ =$0$ {\$displaystystytylease T_T}$$T_{\put },\Rightarrow q_{w}=0$ T ${\displaystyle$T},$$$\mu {\displaystyle }$ ${\displaystyle \mu }$이(가) 도처에 일정하게 나타나므로$$, 압축 불가능한 쿠엣 플로우 용액을 회수한다. Otherwise, one must know the full temperature dependence of ${\displaystyle {\tilde {\mu }}({\tilde {T}})}$. While there is no simple expression for ${\displaystyle {\tilde {\mu }}({\tilde {T}})}$ that is both accurate and general, there are several approximations for certain materials — 예를 들어, 점도의 온도 의존성. When ${\displaystyle \mathrm {M} \rightarrow 0}$ and ${\displaystyle q_{w}\neq 0}$, the recovery quantities become unity ${\displaystyle {\tilde {T}}_{r}=1}$. For air, the values ${\displaystyle \gamma =1.4,\ {\tilde {\mu }}({$$\tilde{T}}={\tilde{T}^{2/3}}}}$이(가) 일반적으로 사용되며$$, 이 경우에 대한 결과는 그림에 나와 있다.

분리 및 이온화의 영향($즉{\displaystyle {}_{}}$, c ${\displaystyle p_{}}$ ${\$$})$도 연구되었다. 이 경우 분자의 분리에 의해 회수 온도가 감소한다.^[7]

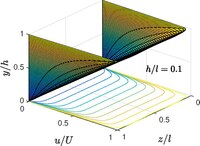
직사각형 채널

1차원 $flow{\displaystyle }$ u${\displaystyle (y}$ )$${\$displaystyle u(y)}$은 두 플레이트가 스트림 방향(${\displaystyle }$ ${\displaystyle x$ 및 스팬 방향(${\displaystyle }$ ${\displaysty$z$\})$에서 무한히 긴 경우에 유효하다$$. 스팬웨이즈 길이가 유한하면 흐름이 2차원이 되고 $u{\displaystyle }$ ${\displaystyle u}$은 x ${\displaystyle x}$와 z ${\displaystyle$ z$}$의 함수다$.$ 다만 흐름의 단방향성을 확보하기 위해서는 스트림 방향의 무한 길이를 유지해야 한다.

예를 들어$,$ 상단 벽이 일정한 $속도{\displaystyle }$ U$${\$displaystyle U}$을(를) 사용하여 이동하는 조건에 따라 가로 $높이{\displaystyle }$ h$${\$displaystyle$h} 및$$ 세로 폭 $l{\displaystyle }${\$displaystyle l}$을(를) 가진 무한히 긴 직사각형 채널을 고려해 보십시오$.$ 가압 경사 없이 Navier–스토크 방정식은 다음으로 감소한다.

${\displaystyle {\frac {\fract ^{2}u}{\frac y^{2}}+{\frac {\frac ^{2}u}{\flash z^{2}}=0}$

.

${\displaystyle u(0,z)=0,\quad u(h,z)=U,}$

${\displaystyle u(y,0)=0,\display u(y,l)=0.}$

변수의 분리를 사용하여 용액은 다음과 같다.

${\displaystyle u(y,z)={\frac {4}U}{\pi }}\sum _{n=1}^{\infty }{\frac {1}{2n-1}}{\frac {\sinh(\beta _{n}y)}{\sinh(\beta _{n}h)}}\sin(\beta _{n}z),\quad \beta _{n}={\frac {(2n-1)\pi }{l}}.}$

${\displaystyle \mathrm{h}}$/ ${\displaystyle l}$ ${\displaystyle \ll }$ 1 ${\displaystyle h/l\ll$ 1}이$($가) 표시되면 그림과 같이 평면 쿠엣 흐름이 복구된다.

실린더

Taylor-Couette 흐름은 무한히 긴 두 회전하는 동축 실린더 사이의 흐름이다.^[8] 원래의 문제는 1845년 스톡스에 의해 해결되었지만,^[9] 제프리 잉그램 테일러는 1923년 유명한 논문에서 그 안정성을 연구했기 때문에 그 흐름에 이름이 붙었다.^[10]

The problem can be solved in cylindrical coordinates ${\displaystyle (r,\theta ,z)}$. Denote the radii of the inner and outer cylinders as ${\displaystyle R_{1}}$ and ${\displaystyle R_{2}}$. Assuming the cylinders rotate at constant angular velocities ${\displaystyle \Omega _{1}}$ and $$${\displaystyle {\mathrm{\Omega }}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$ 그러면 $\theta {\displaystyle }$ ${\displaystyle \theta}$ -방향의$$ 속도는^[11]

${\displaystyle v_{\theta }(r)=ar+{\frac {b}{r}},\qquad a={\frac {\Omega _{2}R_{2}^{2}-\Omega _{1}R_{1}^{2}}{R_{2}^{2}-R_{1}^{2}}},\quad b={\frac {(\Omega _{1}-\Omega _{2})R_{1}^{2}R_{2}^{2}}:{R_{2}^{2}-R_{1}^{2}}.}$

이 방정식은 곡률의 효과가 더 이상 흐름 영역에서 일정한 전단(shear)을 허용하지 않음을 보여준다.

길이가 유한한 동축 실린더

기존의 테일러-쿠엣 흐름 문제는 무한히 긴 실린더를 가정한다. 실린더에 불가결한 유한 길이 $l{\displaystyle }$ ${\displaystyle l}$이$($가) 있는 경우, 분석을 수정해야 한다(흐름이 여전히 단방향이지만). $\Omega {\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$= ${\displaystyle 0}$ ${\displaystyle \Oomega _{2}=0$의 경우 유한 길이 문제는 변수 또는 적분 변환의 분리를 사용하여 해결할 수 있으며,^[12] 다음과 같은 장점이 있다.

${\displaystyle v_{\theta }(r,z)={\frac {4R_{1}\Omega _{1}}{\pi }}\sum _{n=1}^{\infty }{\frac {1}{2n-1}}{\frac {I_{1}(\beta _{n}R_{2})K_{1}(\beta _{n}r)-K_{1}(\beta _{n}R_{2})I_{1}(\beta _{n}r)}{I_{1}(\beta _{n}R_{2})K_{1}(\beta _{n}R_{1}-K_{1}(\beta _{n}R_{2})I_{1}(\beta _{n}R_{1}}})}\sin(\beta _{n}z),\quad \beta _{n}={\frac {(2n-1)\pi },},}$

여기서$$ $I{\displaystyle ({}_{}}$ n ${\displaystyle r_{}}$)${\displaystyle }$, ${\displaystyle \text{K}({}_{}}$ ${\displaystyle n_{}}$ ${\displaystyle {}_{}}$ )${\displaystyle I(\beta _{n}r),\ K(\beta _{n}r)$는 제1종과 제2종의 수정된 베셀 함수다.

참고 항목

• 층류 흐름
• 스톡스-쿠엣 흐름
• 하겐-포이세유 방정식
• 테일러-쿠엣 흐름
• 나비에르에서 나오는 하겐-포이세유유 흐름–스토크 방정식

참조

원천

외부 링크

• AMS 용어집: 쿠엣 흐름
• Rheeologist의 관점: Couette Cell 액세서리의 과학