레이놀즈 수

레이놀즈 수(Re)는 다양한 유체 흐름 상황에서 흐름 패턴을 예측하는 데 도움이 됩니다.레이놀즈 수치가 낮을 경우 흐름은 층류(시트형) 흐름에 의해 지배되는 경향이 있는 반면 레이놀즈 수치가 높을 경우 흐름은 난류적인 경향이 있습니다.난류는 유체의 속도와 방향의 차이로 인해 발생하며, 유체의 전체 방향(에디 전류)과 교차하거나 역방향으로 이동할 수 있습니다.이러한 와전류는 흐름을 휘젓기 시작하고 그 과정에서 에너지를 소모하기 시작하는데, 액체는 캐비테이션의 가능성을 높입니다.레이놀즈 수는 유체역학에서 중요한 무차원량이다.

레이놀즈 번호는 파이프 내 액체 흐름에서 항공기 날개 위의 공기 통로에 이르기까지 다양한 용도로 사용됩니다.층류에서 난류로의 전환을 예측하는 데 사용되며 풍동 내 항공기 모델과 풀사이즈 버전 간 등 유사하지만 다른 크기의 흐름 상황의 스케일링에 사용된다.난류의 시작 예측과 스케일링 효과 계산 능력은 국지적 또는 전지구적 공기 또는 물의 움직임과 같은 대규모 유체 거동을 예측하는 데 사용할 수 있으며 이에 따라 관련된 기상 및 기후 영향도 예측할 수 있다.

이 개념은 1851년 ^[2]조지 스톡스에 의해 도입되었지만, 레이놀즈 번호는 1883년에 ^[4][5]그 사용을 대중화한 오스본 레이놀즈 (1842–1912)의 이름을 따서 1908년^[3] 아놀드 소머펠드에 의해 명명되었다.

정의.

레이놀즈 수치는 유체 속도 차이로 인해 상대적으로 내부 이동되는 유체 내 점성력에 대한 관성력의 비율입니다.이러한 힘이 동작을 변경하는 영역을 파이프 내부의 경계 표면과 같이 경계 레이어라고 합니다.공기 중의 화염에서 방출되는 뜨거운 가스와 같은 저속의 유체에 고속 유체의 흐름을 도입함으로써 유사한 효과를 얻을 수 있습니다.이 상대적인 움직임은 유체 마찰을 발생시켜 난류를 발생시키는 요인입니다.이 효과를 상쇄하는 것은 난류를 억제하는 경향이 있는 유체의 점도입니다.레이놀즈 수치는 주어진 흐름 조건에 대한 이 두 가지 유형의 힘의 상대적 중요성을 정량화하고, ^[6]특정 상황에서 난류가 언제 발생할지를 알려주는 지침이다.

난류의 시작을 예측하는 이 능력은 배관 시스템이나 항공기 날개와 같은 장비에 대한 중요한 설계 도구이지만 레이놀즈 숫자는 유체 역학 문제의 스케일링에도 사용되며 모델 항공기 간과 같은 유체 흐름의 두 다른 사례와 전체 크기 사이의 동적 유사성을 결정하는 데 사용됩니다.버전입니다.이러한 배율은 선형적이지 않으며 레이놀즈 수치를 두 상황에 적용하면 배율 계수를 개발할 수 있다.

층류 및 난류 유동 방식에 관하여:

• 층류(laminar flow)는 낮은 레이놀즈 수에서 발생하며 점성력이 우세하며 부드럽고 일정한 유체 운동을 특징으로 한다.
• 난류 흐름은 높은 레이놀즈 수에서 발생하며 관성력에 의해 지배되며, 이는 혼돈된 에디, 소용돌이 및 기타 흐름 ^[7]불안정성을 생성하는 경향이 있다.

레이놀즈 수는 다음과 같이 정의됩니다^[3].

${\displaystyle \mathrm {Re} = frac {uL} {\nu } = frac {rho uL} {\mu }$

여기서:

• θ는 유체의 밀도(SI 단위: kg³/m)
• u는 유속(m/s)입니다.
• L은 특징적인 선형 치수(m)입니다(예에 대해서는 이 문서의 다음 항 참조).
• μ는 유체의 동적 점도(Pa·s 또는 N·s/m² 또는 kg/(m·s))입니다.
• θ는 유체의² 운동학적 점도(m/s)이다.

레이놀즈 수치는 ^{[n 1]}유체가 표면에 대해 상대적인 움직임을 보이는 몇 가지 다른 상황에 대해 정의할 수 있습니다.이러한 정의에는 일반적으로 밀도 및 점도의 유체 특성, 속도 및 특성 길이 또는 특성 치수(위 등식의 L)가 포함됩니다.이 치수는 관례의 문제이며, 예를 들어 반지름과 직경은 구나 원을 설명하는 데 동일하게 유효하지만 하나는 관례에 따라 선택된다.항공기 또는 선박의 경우 길이 또는 폭을 사용할 수 있습니다.파이프 내 흐름 또는 유체 내를 이동하는 구에 대해서는 일반적으로 내경이 사용됩니다.직사각형 파이프나 비구면 객체와 같은 다른 모양에는 동일한 직경이 정의되어 있습니다.압축성 기체와 같이 밀도가 가변적인 유체 또는 점도가 가변적인 유체(예: 비뉴턴 유체)의 경우 특별한 규칙이 적용된다.속도 또한 일부 상황, 특히 교반된 용기에서는 관례의 문제가 될 수 있습니다.

실제로 레이놀즈 숫자를 맞추는 것 자체로는 유사성을 보장하기에 충분하지 않습니다.유체 흐름은 일반적으로 혼돈적이며, 경계 표면의 형태 및 표면 거칠기의 매우 작은 변화가 매우 다른 흐름을 초래할 수 있습니다.그럼에도 불구하고 레이놀즈 숫자는 매우 중요한 지침이며 널리 사용되고 있습니다.

역사

오스본 레이놀즈는 파이프의 유체 흐름이 층류에서 난류 흐름으로 전환되는 조건을 연구한 것으로 유명하다.1883년 논문에서 레이놀즈는 더 큰 파이프에서 투명한 물의 흐름의 중심에 도입된 염색된 물의 소량을 사용하여 다양한 흐름 속도에서 물의 흐름의 거동을 조사한 고전 실험에서 층류에서 난류 흐름으로의 전환을 설명했습니다.

더 큰 파이프는 유리였기 때문에 염색된 스트림 층의 거동을 관찰할 수 있었습니다.이 파이프의 끝에는 튜브 내부의 수속을 변화시키는 데 사용되는 유량 조절 밸브가 있었다.속도가 낮을 때, 염색된 층은 큰 튜브의 전체 길이에 걸쳐 뚜렷하게 남아 있었다.속도가 증가하면, 그 층은 주어진 지점에서 분해되어 유체의 단면 전체로 확산되었다.이 현상이 발생한 지점은 층류에서 난류로의 전환점이었다.

이러한 실험으로부터 동적 유사성에 대한 무차원 레이놀즈 수, 즉 점성력에 대한 관성력의 비율이 나왔다.레이놀즈는 또한 속도 등의 양이 평균과 변동 성분의 합으로 표현되는 난류 흐름의 레이놀즈 평균이라고 알려진 것을 제안했다.이러한 평균은 예를 들어 레이놀즈 평균 Navier를 사용하여 난류 흐름에 대한 '벌크' 설명을 허용합니다.-방정식을 스토크합니다.

파이프 내 흐름

파이프 또는 튜브의 흐름의 경우 레이놀즈 수는 일반적으로 다음과 같이^[8] 정의됩니다.

$\displaystyle \mathrm {Re} = flac {uD_{\text{H}}}{\nu }} = frac {rho uD_{\text{H}} {\mu } = frac {rho QD _ {\text{H}}}{\mu A}}=param frac {WD_{\text{\text}H}}{\mu A},}$

어디에

• D는_H 파이프의 유압 직경(파이프가 원형인 경우 내경)(m),
• Q는 체적 유량(m³/s)입니다.
• A는 파이프의 단면적(A=.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output .sfra.C.den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}πD2/4)(m2들),.
• u는 유체의 평균 속도(m/s),
• μ(mu)는 유체의 동적 점도이다(Pa·s = N·s/m² = kg/(m·s),
• γ(nu)는 운동학적 점도(θ = μ/s)(m²/s),
• γ(rho)는 유체의 밀도(kg³/m)이다.
• W는 유체의 질량 유량(kg/s)입니다.

높이와 폭이 비교 가능한 정사각형, 직사각형 또는 고리형 덕트와 같은 형상의 경우 내부 흐름 상황에 대한 특성 치수는 다음과 같이 정의된 유압 직경_H D로 간주한다.

$\displaystyle D_{\text{H}}=440frac {4}A}{P}},}$

여기서 A는 단면적, P는 습윤 둘레입니다.채널의 습윤 둘레는 ^[9]흐름과 접촉하는 모든 채널 벽의 총 둘레입니다.즉, 공기에 노출되는 채널의 길이는 습윤 둘레에 포함되지 않습니다.

원형 파이프의 경우 유압 직경은 내부 파이프 직경과 정확히 동일합니다.

$\displaystyle D_{\text{H}}=D.}$

튜브 인 튜브 열 교환기의 외부 채널과 같은 고리형 덕트의 경우, 유압 직경은 대수적으로 나타내어 다음과 같이 줄일 수 있습니다.

$(\displaystyle D_{\text{H,annulus}}=D_{\text{o}}-D_{\text{i}}})$

어디에

• D는_o 외관의 외경이다.
• D는_i 내관의 내경이다.

비원형 덕트 내에서의 흐름과 관련된 계산에서는 덕트 단면의 석면비 AR이 1/4 < AR < ^[10]4의 범위에 머무르면 유압 직경을 적절한 정확도로 대체할 수 있다.

층상-난동 전이

평판 위의 경계층 흐름에서는 일정 길이의 흐름 후 층 경계층이 불안정하고 난류가 발생한다는 것이 실험으로 확인되었습니다.이 불안정성은 다양한 척도와 다양한 유체에^{5 [11]}걸쳐 발생하며, 보통 Re 5 5×10일 때 발생합니다_x. 여기서 x는 평판의 앞쪽 가장자리로부터의 거리이고 유속은 경계층 밖의 유체의 자유 흐름 속도입니다.

직경 D의 파이프 내 흐름의 경우 "완전 전개"^{[n 2]} 흐름의 경우 Re < 2300일 때_D 층류가 발생하고 Re ^[12][13]> 2900일 때_D 난류가 발생하는 것으로 실험 관찰 결과 나타났다.이 범위의 하단에서는 파이프 입구로부터 매우 먼 거리에서만 연속적인 난류가 형성됩니다.중간 흐름은 층류에서 난류로, 그리고 불규칙한 간격으로 층류로 다시 이동하기 시작합니다. 이를 간헐적 흐름이라고 합니다.이는 파이프 단면의 다른 영역에서 파이프 거칠기 및 흐름 균일성 등의 다른 요인에 따라 유체의 속도와 조건이 다르기 때문입니다.관의 빠르게 움직이는 중심에서 층류 흐름이 지배적인 반면 느린 난류 흐름이 벽 근처에서 지배적인 경향이 있습니다.레이놀즈 수가 증가함에 따라 연속 난류 흐름은 유입구에 더 가까이 이동하고 그 사이의 간헐성은 Re > ^[12]2900에서 흐름이_D 완전히 난류가 될 때까지 증가한다.이 결과는 유압 직경을 사용하여 비원형 채널로 일반화되므로 다른 형태의 ^[12]채널에 대한 전이 레이놀즈 수를 계산할 수 있습니다.

이러한 전이 레이놀즈 수들은 임계 레이놀즈 수라고도 불리며,^[5] 1895년경 오스본 레이놀즈가 연구했습니다.임계 레이놀즈 수치는 ^[14]기하학마다 다릅니다.

넓은 덕트에서의 흐름

두 평면 평행 표면 사이를 이동하는 유체의 경우(폭은 플레이트 사이의 공간보다 훨씬 크다), 특성 치수는 ^[15]플레이트 사이의 거리와 같다.이는 위의 고리형 덕트 및 직사각형 덕트 케이스를 제한 석면비로 적용한 것과 일치한다.

개방된 채널에서의 흐름

표면이 자유로운 액체 흐름의 경우 유압 반경을 결정해야 합니다.이것은 채널의 단면적을 습윤 둘레로 나눈 것입니다.반원형 채널의 경우 직경의 4분의 1입니다(파이프 흐름이 꽉 찬 경우).직사각형 채널의 경우 유압 반지름은 단면적을 습윤 둘레로 나눈 값입니다.그런 다음 일부 텍스트는 파이프 ^[16]흐름에서와 같은 난류 시작 시 Re 값을 제공하기 때문에 유압 반지름의 4배인 특성 치수를 사용하는 반면, 다른 텍스트는 천이 및 난류 흐름에 대해 Re 값이 다른 특성 길이 척도로 유압 반지름을 사용합니다.

에어포일 주위에 흐르다

레이놀즈 수치는 (특히) 특성을 계산/비교할 때 "스케일 효과"를 관리하기 위해 에어포일 설계에 사용됩니다(크게 조정된 작은 날개에서는 성능이 ^[17]달라집니다).유체역학자는 코드 레이놀즈수 R을 다음과 같이 정의한다.여기서 V는 비행속도, c는 코드길이, θ는 에어포일이 작동하는 유체의 운동학적 점도로 해수면 대기 ^[18]중 1.460×10m⁻⁵²/s이다.일부 특수 연구에서는 코드 이외의 고유 길이를 사용할 수 있다. 드물지만 "스판 레이놀즈 수"는 여전히 코드가 사용되는 ^[19]날개의 스판 웨이즈 스테이션과 혼동해서는 안 된다.

유체 중의 물체

입자 레이놀즈 수라고 불리며 종종 Re로 표기되는_p 유체 내에서 움직이는 물체의 레이놀즈 수는 주변 흐름의 특성과 낙하 속도를 특징짓습니다.

점성이 있는 유체 중

이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 소스되지 않은 자재는 제거될 수 있습니다. (2014년 2월) (이 템플릿 메시지 삭제 방법 및 시기에 대해 알아보기)

고분자 용액이나 고분자가 녹는 것과 같이 점도가 자연적으로 높을 경우 흐름은 일반적으로 층상입니다.레이놀즈 수치는 매우 작으며 Stokes의 법칙을 사용하여 유체의 점도를 측정할 수 있습니다.구체는 유체를 통해 낙하할 수 있으며, 점도를 결정할 수 있는 종단 속도에 빠르게 도달합니다.

고분자 용액의 층류 흐름은 물고기나 돌고래와 같은 동물들에 의해 이용되며, 그들은 수영하는 동안 그들의 몸 위로 흐르는 것을 돕기 위해 피부에서 점성이 있는 용액을 배출한다.물에 저분자량 폴리옥시에틸렌 등의 폴리머 용액을 선체 습윤 표면에 퍼올려 속도 우위를 점하려는 소유주들이 요트 레이싱에서 사용해 왔다.

그러나 고분자 혼합에는 난류가 (예를 들어) 미세한 필러를 재료를 통해 분배하기 위해 필요하기 때문에 문제가 됩니다."캐비티 트랜스퍼 믹서"와 같은 발명품은 혼합 효율을 향상시키기 위해 여러 개의 접힘을 이동 용융물로 만드는 것을 개발하였다.이 장치는 혼합을 돕기 위해 압출기에 장착할 수 있습니다.

유체 중의 구

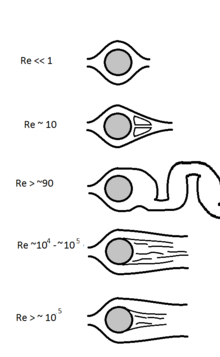
유체 중 구체의 특징적인 길이 척도는 구체의 지름이며, 특징적인 속도는 구체의 운동이 기준 유체 구획을 방해하지 않도록 구에서 다소 떨어진 유체에 대한 상대적인 속도이다.밀도와 점도는 ^[20]유체에 속하는 밀도입니다.이 정의에 따르면 순수 층류(layer flow)는 Re 。

낮은 Re 조건 하에서 힘과 운동 속도의 관계는 스톡스의 ^[21]법칙에 의해 주어진다.

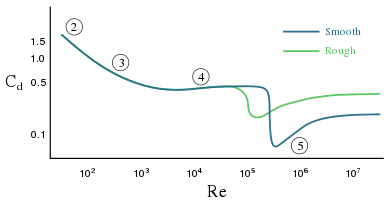
레이놀즈 수치가 높을수록 구면에서의 항력은 표면 거칠기에 따라 달라집니다.따라서 예를 들어 골프공 표면에 딤플을 추가하면 볼 상류측 경계층이 층류에서 난류로 전이된다.난류 경계층은 층계보다 훨씬 오랫동안 볼 표면에 부착되어 있을 수 있으며, 따라서 더 좁은 저압 웨이크를 생성하므로 압력 항력이 줄어듭니다.압력 항력이 감소하면 공이 ^[22]더 멀리 이동합니다.

유체 중의 직사각형 물체

직사각형 물체의 방정식은 구체의 방정식과 동일하며, 물체는 타원체로 근사되고 길이 축은 특성 길이 척도로 선택됩니다.이러한 고려사항은 완벽한 구형 입자가 거의 없는 자연 흐름에서 중요하다.각 축의 측정이 실용적이지 않은 입자의 경우, 특징적인 입자 길이 척도로 체 지름을 대신 사용한다.두 근사치 모두 임계 레이놀즈 수의 값을 변경합니다.

낙하 속도

입자 레이놀즈 수는 입자의 낙하 속도를 결정하는 데 중요합니다.레이놀즈 입자가 층류임을 나타내는 경우 스톡스의 법칙을 사용하여 낙하속도를 계산할 수 있습니다.입자 레이놀즈 수가 난류를 나타내는 경우, 적절한 침하 속도를 모델링하기 위해 난류 드래그 법칙을 구성해야 합니다.

패킹 베드

접촉하는 직경 D의 대략적인 구면 입자의 층을 통과하는 유체 흐름의 경우, 보이디지가 θ이고 표면 속도가 v이면_s 레이놀즈 수는 다음과 같이 정의될^[23] 수 있다.

$\displaystyle \mathrm {Re} = frac {rho v_{\text{s}}D}{\mu }},}$

또는

$\displaystyle \mathrm {Re} = frac {rho v_{\text{s}}D}{\mu \varepsilon }}}$

또는

$\displaystyle \mathrm {Re} = frac {rho v_{\text{s}}D}{\mu(1-\varepsilon)}}.}$

방정식의 선택은 관련된 시스템에 따라 달라집니다. 첫 번째 방법은 다양한 유형의 충전 및 유동층 데이터를 성공적으로 상관하고, 두 번째 레이놀즈 숫자는 액상 데이터에 적합하며, 세 번째 방법은 유동층 데이터를 성공적으로 상관하고, 첫 번째 방법은 액상 유동층 ^[23]시스템에 도입되었습니다.

층상 조건은 Re = 10까지 적용되며 Re = ^[20]2000부터는 완전 난류이다.

교반 용기

중심회전 패들, 터빈 또는 프로펠러에 의해 교반되는 원통형 용기에서 특성 치수는 교반기 D의 직경이다.속도 V는 ND입니다.여기서 N은 초당 rad 단위의 회전 속도입니다.레이놀즈 번호는 다음과 같습니다.

$(\displaystyle \mathrm {Re} = frac {rho ND^{2}} {\mu}} = frac {rho VD} {\mu } ).}$

Re 값이 ^[24]10000보다 클 경우 시스템은 완전 난류입니다.

파이프 마찰

파이프를^[25] 통해 완전히 발달된 유체의 흐름에 대해 나타나는 압력 강하는 레이놀즈 수 Re에 대한 Darcy-Weisbach 마찰 계수 f와 상대 거칠기 θ/D를 나타내는 Moody 다이어그램을 사용하여 예측할 수 있다.이 다이어그램은 레이놀즈 수가 증가함에 따라 층류, 전이 및 난류 흐름을 명확하게 보여줍니다.파이프 흐름의 특성은 흐름이 층류인지 난류인지에 따라 크게 좌우됩니다.

흐름의 유사성

두 흐름이 비슷하려면 기하학이 동일해야 하며 레이놀드와 오일러 수가 같아야 합니다.모델의 해당 지점과 실제 흐름에서의 유체 거동을 비교할 때 다음과 같은 조건을 충족됩니다.

${\displaystyle {\text{m}}&=\mathrm {Re},\\mathrm {Eu},=\mathrm {Eu},\end{aligned}}}$

$여기$서 ${\displaystyle {\mathrm{R}}_{}}$ ${\displaystyle {}_{}}$ m$${\$displaystyle \mathrm {Re} _{\text{m}}}$은 모델의 레이놀즈 $번호$이고, ${\displaystyle \mathrm{R}}$e {\$displaystyle \mathrm${Re$}}$은 풀 스케일 레이놀즈 번호이며, 오일러 번호도 이와 유사합니다.

모델 번호와 설계 번호는 동일한 비율이어야 합니다. 따라서

${\displaystyle {p_{\text{m}}{\rho_{\text{m}}}v_{\text{m}^{2}}=black {p}{\rho v^{2}}}.}$

이를 통해 엔지니어는 수로 또는 풍동에서 축소 축소 모델을 사용하여 실험을 수행하고 데이터를 실제 흐름과 연관시켜 실험 중 및 실험실 시간을 절약할 수 있습니다.진정한 동적 유사성은 압축 가능한 흐름에서 사용되는 마하 수나 오픈채널 흐름을 제어하는 Froude 수 등 다른 치수 없는 숫자와 일치해야 할 수도 있습니다.일부 흐름은 사용 가능한 장치 및 유체로 실질적으로 만족할 수 있는 것보다 더 많은 치수 없는 매개변수를 포함하므로 어떤 매개변수가 가장 중요한지 결정해야 합니다.실험 흐름 모델링이 유용하려면 상당한 경험과 엔지니어의 판단이 필요합니다.

단순한 레이놀즈 수로는 흐름의 유사성에 충분하지 않은 예(또는 흐름 상태 - 층류 또는 난류)는 유계 흐름, 즉 벽이나 다른 경계에 의해 제한된다.이것의 전형적인 예는 테일러-쿠엣 흐름이며, 여기에서 경계 실린더의 무차원 비율도 중요하며, 이러한 구별이 중요한 역할을 ^[26][27]하는 많은 기술적 응용 분야이다.이러한 제한의 원칙은 모리스 마리 알프레드 쿠에트와 제프리 잉그램 테일러에 의해 개발되었고 플로리스 타켄스와 데이비드 루엘에 의해 더욱 발전되었다.

레이놀즈^[28][29] 수의 일반적인 값

• 세균~ 1 × 10⁻⁴
• 섬모 ~ 1 × 10⁻¹
• 가장 작은 물고기~1마리
• 뇌의 혈류~ 1 × 10²
• 대동맥 혈류 ~ 1 × 10³
• 경계층의 경우 10으로 가는⁶ 파이프 흐름의 경우 난류 시작 ~ 2.3 × 10³ ~ 5.0 × 10⁴
• 메이저리그의 일반적인 투구 ~ 2 × 10⁵
• 사람 수영~ 4 × 10⁶
• 가장 빠른 물고기~ 1 × 10⁸
• 청고래~ 4 × 10⁸
• 큰 배 (엘리자베스 여왕 2) ~ 5 × 10⁹
• 열대 저기압~1 x 10¹²

난류 운동의 최소 척도

이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2019년 1월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

난류에서는 시변하는 유체운동의 스케일 범위가 있다.유체 운동의 가장 큰 스케일(에디라고도 함)의 크기는 흐름의 전체 형상에 따라 설정됩니다.예를 들어, 산업용 스모크 스택에서 유체 이동의 가장 큰 척도는 스택 자체의 지름만큼 큽니다.가장 작은 척도의 크기는 레이놀즈 수로 설정됩니다.레이놀즈 수치가 증가함에 따라 흐름의 규모가 점점 더 작아집니다.매연 스택에서 매연은 크고 부피가 큰 에지 외에도 매우 작은 속도 섭동 또는 에지를 많이 가지고 있는 것으로 보일 수 있습니다.이런 의미에서 레이놀즈 수는 흐름의 척도 범위를 나타내는 지표입니다.레이놀즈 값이 클수록 척도 범위가 넓어집니다.가장 큰 에디는 항상 같은 크기이며 가장 작은 에디는 레이놀즈 수로 결정됩니다.

이 현상에 대한 설명은 무엇입니까?레이놀즈 수치가 크면 흐름의 큰 규모에서 점성력이 중요하지 않다는 것을 나타냅니다.점성력보다 관성력이 우세할 경우, 유체 운동의 가장 큰 스케일은 감쇠되지 않습니다. 즉, 운동을 분산시킬 수 있는 점도가 충분하지 않습니다.운동 에너지는 점도가 중요해질 정도로 작은 수준에 도달할 때까지 이러한 큰 스케일에서 점진적으로 작은 스케일로 "캐스케이드"되어야 한다(점성력은 관성력과 같은 수준이 된다).이 작은 규모에서 마침내 점성 작용에 의한 에너지 소산이 일어납니다.레이놀즈 숫자는 이러한 점성 산산이 발생하는 척도를 나타냅니다.

생리학에서

이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2014년 12월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

체내 혈액순환에 대한 푸아세유의 법칙은 층류 ^[30]흐름에 달려있다.난류에서 유속은 층류에서 압력 구배에 대한 정비례와 대조적으로 압력 구배의 제곱근에 비례합니다.

레이놀즈 수의 정의를 사용하면 혈액의 밀도가 높은 큰 직경이 난기류를 향하고 있음을 알 수 있습니다.혈관 직경이 빠르게 변화하면 좁은 혈관이 더 큰 혈관으로 넓어지는 등 난류가 발생할 수 있습니다.또한 청진기로 가청 난류를 검출할 수 있는 난류의 원인이 아테로마의 팽대부일 수 있다.

복잡한 시스템

레이놀즈 수 해석은 임의의 복잡한 시스템 영역으로 확장되었다.금융 흐름,^[31] 비선형 네트워크 ^{[citation needed]}등후자의 경우 인공 점도는 복잡한 네트워크 미디어에서 에너지 분배의 비선형 메커니즘으로 환원된다.레이놀즈 숫자는 개방 경계 시스템에 대한 주입 에너지 흐름과 소멸 에너지 흐름 간의 균형을 나타내는 기본 제어 매개변수를 나타냅니다.레이놀즈 임계 정권은 가속기(매력기)와 감속기의 ^[32]두 가지 유형의 위상 공간 운동을 분리하는 것으로 나타났다.레이놀즈 수치가 높으면 이상한 유인기 모델의 프레임에서만 혼란스러운 정권 전이가 발생합니다.

파생

레이놀즈 수치는 압축할 수 없는 Navier의 비차원 형식을 사용할 때 얻을 수 있습니다.–라그랑주 도함수로 표현되는 뉴턴 유체에 대한 스토크스 방정식:

$\displaystyle \rho {D\mathbf {v} {Dt}}=-\nabla p+\mu \mathbf ^{2}\mathbf {v} +\rho \mathbf {f}}$

위의 방정식의 각 항은 밀도 곱하기 가속도의 동일한 치수를 갖는 "체력"(단위 부피당 힘)의 단위를 가진다.따라서 각 항은 흐름의 정확한 측정에 의존합니다.방정식을 비차원으로 표현하면, 즉 기본 방정식의 역단위를 갖는 인자에 곱하면, 물리적 크기에 직접적으로 의존하지 않는 형태를 얻을 수 있습니다.비차원 방정식을 얻을 수 있는 한 가지 가능한 방법은 전체 방정식에 인자를 곱하는 것이다.

$(\displaystyle {\frac {L}{\rho V^{2}})$

어디에

• V는 유체(m/s)에 상대적인 평균 속도, v 또는 v이다.
• L은 특성 길이(m)이다.
• θ는 유체 밀도(kg³/m)이다.

지금 설정해당장

$(\displaystyle\mathbf {v} '&=frac {mathbf {v} {V},&p' &=p{\frac {1},&\mathbf {f} {f} {f} {f} {f} {f} {f} {f},&\frac {v},&amp;frac {f},$

나비에를 다시 쓸 수 있어–차원이 없는 스토크스 방정식:

${\displaystyle {D\mathbf {v} {Dt'}=-\nabla 'p'+{\frac {mu}{\rho LV}}\nabla '{2}\mathbf {v}'+\mathbf {f},}$

여기서 μ/160LV = 1/Re이다.

마지막으로 읽기 쉽도록 소수점 삭제:

${\displaystyle {D\mathbf {v} {Dt}}=-\nabla p+{\frac {1}{\mathrm {Re}}}}\displaystyle ^{2}\mathbf {v} +\mathbf {f}}$

이것이 같은 레이놀즈 수를 가진 수학적으로 모든 뉴턴의 압축 불가능한 흐름이 비슷한 이유입니다.또한 위의 방정식에서는 Re → θ에 대해 점성 항이 사라집니다.따라서 레이놀즈 수가 높은 흐름은 자유 스트림에서 거의 무의미합니다.

다른 차원 없는 매개 변수와의 관계

유체역학에는 많은 무차원적인 수가 있다.레이놀즈 수치는 속도장 내 구조물에 대한 이류 및 확산 효과의 비율을 측정하므로, 온도 및 자기장 등 흐름에 의해 전달되는 다른 장에 대한 이러한 효과의 비율을 측정하는 Péclet 수치와 밀접한 관련이 있다.Re의 키네마틱 점도 θ = μ/μ를 열 또는 자기 확산도로 치환하면 각각 열 Péclet 수와 자기 레이놀즈 수가 된다.따라서 이것들은 확산성 비율(프란틀 수 및 자기 프란틀 수)의 Re와 관련이 있다.

「 」를 참조해 주세요.

• 레이놀즈 수송 정리 – 라이프니츠 적분 법칙의 3차원 일반화
• 드래그 계수 – 유체 저항을 정량화하기 위한 무차원 파라미터
• 퇴적물(지질) – 퇴적물, 토양, 암석이 지형 또는 육지에 첨가되는 지질학적 과정
• 켈빈-헬름홀츠 불안정성

레퍼런스

각주

인용문

원천

추가 정보

외부 링크

• 레이놀즈 숫자 at Sixty Symbols
• 레이놀즈 미니 전기사진과 맨체스터 대학의 오리지널 장비 사진.