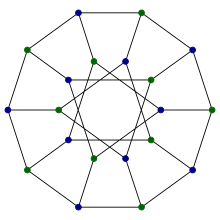
데스아게네스 그래프

데스아게네스 그래프
이름을 따서 명명됨	제라드 데사게스
정점	20
가장자리	30
반지름	5
지름	5
둘레	6
자동형성	240(S5× Z/2Z)
색수	2
색도 지수	3
속	2
책두께	3
대기열 번호	2
특성.	큐빅 거리-정규어 해밀턴어 양립자 대칭
그래프 및 모수 표

그래프 이론의 수학 분야에서 데스아게스 그래프는 20개의 정점과 30개의 가장자리를 가진 거리 변환 입방 그래프다.^[1]지라드 데스아게스의 이름을 따 지었고, 여러 가지 다른 조합 구성에서 발생하며, 대칭성이 높으며, 유일하게 알려진 비 평면 입방체 부분 큐브로서 화학 데이터베이스에 적용되었다.

"Descarges graph"라는 명칭은 또한 20 Vertex Descarges 그래프의 2분의 1로 형성될 수 있는 피터슨 그래프의 보완인 10 Verten 그래프는 20 Vertex Desarges 그래프의 2분의 1로 형성될 수도 있다.^[2]

시공

Desarguees 그래프를 구성하는 몇 가지 다른 방법이 있다.

• 일반화된 피터슨 그래프 G(10, 3)이다.이런 식으로 데스칼레스 그래프를 구성하려면 정점 중 10개를 일반 십각형으로 연결하고 나머지 열 개의 정점을 두 번째 십각형으로 거리 3의 정점 쌍을 연결하는 10점 별에 연결한다.데스아게네스 그래프는 이들 두 폴리곤의 20개 가장자리와 함께 한 데카곤의 10개 가장자리와 다른 데카곤의 해당 점으로 추가로 연결된다.
• 데스바게스의 구성을 나타낸 리바이스 그래프다.이 구성은 두 개의 원근 삼각형, 그들의 관점의 중심, 그리고 그들의 관점의 축을 설명하는 10개의 점과 10개의 선으로 구성되어 있다.Desargues 그래프는 각 점에 대해 하나의 꼭지점, 각 선에 대해 하나의 꼭지점, 모든 입사 점 선 쌍에 대해 하나의 가장자리를 가진다.17세기 프랑스의 수학자 제라드 데사게스의 이름을 딴 데사게스의 정리는 이러한 구성을 이루는 일련의 점들과 선들을 묘사하고 있으며, 그 구성과 그래프는 그것에서 그들의 이름을 따온 것이다.
• 그것은 피터슨 그래프의 초당적 이중 커버로, 각 피터슨 그래프 꼭지점을 정점 쌍으로 교체하고 각 피터슨 그래프 가장자리를 교차된 가장자리 쌍으로 교체함으로써 형성된다.
• 그것은 초당적 Kneser 그래프 H이다_5,2.그것의 정점은 10개의 2요소 부분 집합과 5요소 집합의 10개의 3요소 부분 집합으로 라벨을 붙일 수 있으며, 해당 집합 중 하나가 다른 집합의 부분 집합일 때 두 개의 정점을 연결하는 가장자리가 있다.동등하게, 데스아게스 그래프는 무게 2와 무게 3의 정점에 의해 결정되는 5차원 하이퍼큐브의 유도 서브그래프다.
• 데스칼레스 그래프는 해밀턴식이며 LCF 표기법 [5,-5,9,-9]⁵으로 구성할 수 있다.에르드제스가 k 양성으로 추측했듯이 k와 k+1의 정점에 의해 유도된 2k+1차원 하이퍼큐브의 하위그래프가 해밀턴식이라고, 데스아게스 그래프의 해밀턴성은 놀라운 것이 아니다.(몇 가지 알려진 역추정을 제외하고 모든 정점 변환 그래프에 해밀턴 사이클이 있다는 것은 로바스츠의 더 강한 추측에서도 나타난다.)

대수적 특성

데스아게네스 그래프는 대칭 그래프로서, 다른 정점에 도달하는 정점과 다른 에지에 도달하는 모든 에지를 갖는 대칭 그래프를 가지고 있다.그것의 대칭 그룹은 순서 240을 가지며, 순서 2의 그룹이 있는 5개의 점에서 대칭 그룹의 곱에 이형적이다.

이 대칭 그룹의 제품표현을 데스아게스 그래프의 구성으로 해석할 수 있다: 5개의 점에 대한 대칭집단은 데스아게스 구성의 대칭집단이며, 순서 2 하위집단은 데스아게스 구성의 포인트를 나타내는 정점들의 역할과 반복하는 정점들의 역할을 교환한다.nt 선또는, 초당적 K네서 그래프의 관점에서, 5개의 점의 대칭 집단은 5개의 점의 2-요소와 3-요소의 하위 집합에 대해 별도로 작용하며, 하위 집합의 보완은 하나의 하위 집합 유형을 다른 것으로 변환하는 순서 2의 그룹을 형성한다.5개 점의 대칭군 역시 피터슨 그래프의 대칭군이며, 순서 2 부분군은 이중 커버 구조에서 형성된 각 정점 쌍 내의 정점을 교환한다.

일반화된 피터슨 그래프 G(n, k)는 n = 10과 k = 2 또는 k k² ±1(mod n)인 경우에만 정점 변환이고 (n, k) = (4, k), (5, 2), (8, 3), (10, 3) (10, 3), (12, 5), (24, 5) 7가지 경우에 한한다.^[3]그래서 데스아게네스 그래프는 7개의 대칭적인 일반화된 피터슨 그래프 중 하나이다.이 7개의 그래프 중에는 입체 그래프 G(4, 1)와 피터슨 그래프 G(5, 2), 뫼비우스-칸토르 그래프 G(8, 3)와 도데카헤드 그래프 G(10, 2)와 나우루 그래프 G(12, 5)가 있다.

데스아게네스 그래프의 특징적인 다항식은

${\displaystyle (x-3)(x-2)^{4}(x-1)^{5}(x+1)^{5}(x+2)^{4}(x+3).\,}$

따라서 데스아게네스 그래프는 적분 그래프로서 스펙트럼은 전적으로 정수로 구성된다.

적용들

화학에서 데스아게스 그래프는 데스아게스 그래프로 알려져 있다.Levi graph; 5리간드 화합물의 스테레오이오머 시스템을 구성하는 데 사용된다.이 응용 프로그램에서 그래프의 30개 가장자리는 리간드의 유사점에 해당한다.^[4][5]

기타 속성

데스아그레스 그래프는 직선으로 교차하는 숫자 6을 가지고 있으며 교차 번호를 가진 가장 작은 입방 그래프다(OEIS에서 순서 A110507).이것은 유일하게 알려진 비 평면 입방체 부분 입방체 입니다.^[6]

Desargues 그래프는 색도 번호 2, 색도 지수 3, 반지름 5, 직경 5, 둘레 6을 가지고 있다.또한 3베르크스로 연결된 3베르크스와 3엣지로 연결된 해밀턴의 그래프이기도 하다.책 두께 3과 줄 2가 있다.^[7]

세제곱 거리-정규 그래프는 모두 알려져 있다.^[8]데스아게네스 그래프는 그러한 13개의 그래프 중 하나이다.

데스아게네스 그래프는 6속(Desargue)의 비방향성 다지관(Non-Orie)에 12각형 면의 자기-페트리 이중 정규 지도로 삽입할 수 있다.

갤러리

• 

  다양한 사이클을 강조하기 위해 색칠된 논쟁 그래프.

• 

  데스칼레스 그래프의 색지수는 3이다.

• 

  데스칼레스 그래프의 색수는 2이다.

참조