t분포 확률적 인접 매입

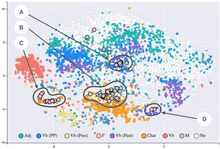
통계에 관한 시리즈의 일부
데이터 시각화
주요 치수
탐색적 데이터 분석 정보 설계 대화형 데이터 시각화 기술 통계 추리통계 통계 그래픽스 줄거리. 데이터 분석 인포그래픽 데이터 과학
중요 인물
타마라 먼즈너 벤 쉬나이더맨 존 W. 투키 에드워드 터프테 사이먼 워들리 한스 로슬링 데이비드 맥캔들리스 알렉산더 오스터발더 에드 호킨스 해들리 위컴 릴랜드 윌킨슨 마이크 보스톡 제프리 히어 이하브 일리아스
정보 그래픽 유형
꺽은선형 차트 막대 그래프 히스토그램 산점도 상자 그림 파레토 차트 파이 차트 영역도 트리 맵 버블 차트 스트라이프 그래픽스 관리도 런 차트 줄기와 잎 표시 카트로그램 스몰 멀티플 스파크라인 테이블 마리메코 차트
관련 토픽
데이터. 정보 빅데이터 데이터베이스 차트정크 시각 지각 회귀 분석 통계 모형 잘못된 그래프
v t

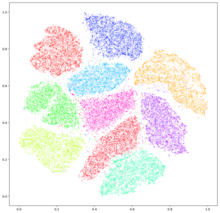
t-분산 확률 인접 임베딩(t-SNE)은 각 데이터 포인트에 2차원 또는 3차원 맵의 위치를 제공하여 고차원 데이터를 시각화하는 통계 방법이다.이것은 원래 Sam Roweis와 Geoffrey Hinton에 ^[1]의해 개발된 확률적 이웃 임베딩에 기초하고 있으며, 여기서 Laurns van der Maatten은 t-분포형 ^[2]변종을 제안했다.이 기술은 2차원 또는 3차원의 저차원 공간에 시각화를 위한 고차원 데이터를 삽입하는 데 적합한 비선형 차원 축소 기술입니다.특히, 비슷한 물체는 인근 점으로 모델링하고 다른 물체는 높은 확률로 먼 점으로 모델링하는 방식으로 각 고차원 물체를 2차원 또는 3차원 점으로 모델링합니다.

t-SNE 알고리즘은 2개의 주요 단계로 구성됩니다.첫째, t-SNE는 유사한 객체가 더 높은 확률로 할당되는 반면 다른 점은 더 낮은 확률로 할당되는 방식으로 고차원 객체의 쌍에 대한 확률 분포를 구성한다.둘째, t-SNE는 저차원 지도의 지점들에 걸쳐 유사한 확률 분포를 정의하며, 지도의 지점 위치에 관해 두 분포 사이의 쿨백-라이블러 발산(Kullback-Leibler divergence, KL divergence)을 최소화한다.원래 알고리즘은 유사성 측정 기준의 기준으로 객체 간의 유클리드 거리를 사용하지만, 이것은 적절히 변경될 수 있다.

t-SNE는 유전체학, 컴퓨터 ^[3]보안 연구, 자연어 처리, ^[4]음악 분석, 암 연구,^[5] 생물 ^[6]정보학, 지질 ^[7][8][9]영역 해석 및 생물의학 신호 ^[10]처리를 포함한 광범위한 애플리케이션에서 시각화에 사용되어 왔다.

t-SNE 그림은 종종 군집을 표시하는 것처럼 보이지만 시각 군집은 선택한 모수화의 영향을 강하게 받을 수 있으므로 t-SNE에 대한 모수를 잘 이해해야 합니다.이러한 "클러스터"는 비클러스터 데이터에도 ^[11]나타나므로 잘못된 발견일 수 있습니다.따라서 매개 변수를 선택하고 ^[12][13]결과를 검증하기 위해 대화형 탐사가 필요할 수 있습니다.t-SNE는 종종 잘 분리된 클러스터를 복구할 수 있으며, 특별한 매개 변수 선택으로 단순한 형태의 스펙트럼 ^[14]클러스터링에 가깝다는 것이 입증되었다.

세부 사항

$N개(\displaystyle$$N개$)의$$ 고차원 $객체{\displaystyle {\mathbf{}}_{}}$ x ${\displaystyle {\mathrm{}}_{}}$,${\displaystyle \dots ,}$ ${\displaystyle {\mathbf{}}_{}}$(\$displaystyle \$$mathbf {x}_{$1},\$dots,\mathbf$${x$$}_$$$${N})$가 $주어진{\displaystyle }$ 경우 t-SNE는 먼저$$${\displaystyle {}_{}}$의 $유사성$에 비례하는 ${\displaystyle {\mathrm{확률}}_{}}$을 $계산합니다.$$(\displaystyle$ \$mathbf {x} _{$j$\}),$ 다음과 같습니다.

$i{\displaystyle j}$j \ $displaystyle$i \ $neq$ j$,$ 、

${\displaystyle p_{j\mid i}=parc frac {exp(-\lVert \mathbf {x}_{j}\rVert ^{2}/2\parc_{i}}{\sum _k\neq i}\exp(-\lVert \mathbf {x}_x}_i} _xp}$

$p{\displaystyle {}_{}}$ ${\displaystyle i_{}\mathrm{i}}$ i ${\displaystyle {}_{}}$0 { $display$ style p$_$ {$i$ \ $mid$ i } =$0$。$모든{\displaystyle }$i { $display style$ i$$}에 ${\displaystyle \underset{}{대해}}{\displaystyle \underset{}{}{}_{}}$ ${\displaystyle p_{}}$ ${\displaystyle j_{}}$ ${\displaystyle \mathrm{i}}$ 1 {$displaystyle$ \$sum$_ {$j$ \ mid i } $= 1$ 입니다.

Van der Maatten과 Hinton은 다음과 같이 설명합니다.「 datappoint $x{\displaystyle {}_{}}$ ( $display$ style $x$_ {$$$j$$$} )와$$ $datappoint{\displaystyle {}_{}}$ x$$ ( $display$ style $x$_ {$$$i$$$} )의 유사성은 조건적인 $확률$입니다.${\displaystyle p_{}}$${\displaystyle j_{}}$i ( x { $display style$ $p$_ { $i$} } ） 。이웃은 $(\$i})$$^[2]에 중심을 둔 가우스에서 확률 밀도에 비례하여 선택되었다."

정의하다

${\displaystyle p_{ij}=p_{j\midi}+p_{i\mid j}}{2N}}}$

$p$ i ${\displaystyle j_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle j_{}}$ i$$${\displaystyle {}_{}}$ $p_${$ij$}$$$=$ $p_{ji$}$$$}$ , p ${\displaystyle \underset{}{}{}_{}}$$$$=$ $0{\displaystyle {}_{}}$ { ${\displaystyle {\mathrm{displaystyle}}_{}}$ p_${\displaystyle \underset{}{\{\mathrm{ii}}}$} ${\displaystyle {}_{}}$ ${\displaystyle 1}$$${ $displaystyle \sum$_ {$i,j} p_{ij$}$$=$1$.

가우스 커널$$ i \ $displaystyle \sigma$_ { $i}$의 대역폭은 조건분포의 난이도가 이분법을 사용하여 미리 정의된 난이도와 같도록 설정됩니다.그 결과 대역폭은 데이터 밀도에 맞게 조정됩니다.데이터 공간의 밀도가 높은 부분에서는 작은 값인 ${\displaystyle {\theta }_{}}$i $\sigma$ _${i}$가 사용됩니다.

가우스 커널은 유클리드 거리${\displaystyle {}_{}}$ ${\displaystyle x_{}}$i - ${\displaystyle x_{}}$ j $†$ { $displaystyle \lVert x_{i}-x_{j}\rVert$를 사용하기 때문에 차원성의 저주에 영향을 받고 거리가 식별 능력을 상실하면 ${\displaystyle {\mathrm{pi}}_{}}$ j$${ $displaystyle p_{ij}$가 매우 유사해집니다(점적으로 수렴됩니다).ge to constant).이를 ^[15]완화하기 위해 각 점의 고유 치수에 기초하여 멱변환으로 거리를 조정하는 것이 제안되었다.

t-SNE는 d$${\$displaystyle$ d$}$ 차원$$ $맵{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ 1,${\displaystyle \dots ,}$ ${\displaystyle {}_{}}$ {$style \mathbf {y}$ _${1},\dots,\mathbf$$${$y}$ _${N}$ (${\displaystyle {}_{}}$ i${\displaystyle {}_{}{}^{}}$R \ $displaystyle \mathbbf {y}$_${i}$ \$in$ \$mathbr })$ $display$ $^}$ $d$를 $학습$하는 것을 $목표$로 합니다.$({displaystyle p_{ij$$}}})$ 가능한 한 많이 사용합니다.이를 위해 매우 유사한 접근방식을 사용하여 $지도$의 두 점 $\$ $\$$mathbf {y}_$${$$ij}$와 y$$j\$displaystyle$ \$mathbf$ {$y}_{$j$\}$ 사이의 $유사성{\displaystyle {}_{}}$ $q_ij}$를 측정합니다.구체적으로는 i${\displaystyle j}$j { $display style$i \ $neq$j$$}의 경우 ${\displaystyle q_{}}$ ${\displaystyle i_{}}$j { $display$ style $q$_ { $ij$}를$$ 다음과 같이 $정의$합니다.

${\displaystyle q_{ij}=slfrac {(1+\lVert \mathbf {y}_{i}-\mathbf {y}_{j}\rVert ^{2}}{\sum _{k}\neq k}(1+\lVert \mathbf {y}_y}_mathb}_y}_mathb}$

${\displaystyle q_{}}$ ${\displaystyle i_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle 0}$ {$display$ style $q$_ { $ii$ } = 0 으로 설정합니다$.$여기서 헤비테일 Student t-분포(자유도 1도, 코시분포와 동일)는 지도에서 멀리 떨어진 다른 객체를 모델링할 수 있도록 저차원 점 사이의 유사성을 측정하는 데 사용됩니다.

맵에서 $(\$의 위치는 $분포{\displaystyle }$Q(\$displaystyle$ Q$)$에서 $분포{\displaystyle }$P(\$displaystyle$ P$)$의 (비대칭) Kullback-Leibler 차이를 최소화함으로써 결정됩니다.

$\displaystyle \mathrm {KL} \left(P\parallel Q\right)=\sum _{i\neq j}p_{ij}\log {frac {p_{ij}}{q_{ij}}}}$

$(\$ _${i$}) $지점$에 대한 쿨백-라이블러 발산 최소화는 경사 강하를 사용하여 수행된다.이 최적화의 결과는 고차원 입력 간의 유사성을 반영하는 지도입니다.

소프트웨어

• R 패키지 Rtsne은 R에 t-SNE를 실장하고 있습니다.
• ELKI에는 tSNE가 포함되어 있으며 반즈-허트 근사도 포함되어 있습니다.
• Python에서 인기 있는 기계 학습 툴킷인 Scikit-learn은 정확한 솔루션과 반즈-허트 근사치를 모두 사용하여 t-SNE를 구현합니다.
• TensorFlow와 관련된 시각화 키트인 Tensorboard도 t-SNE(온라인 버전)를 구현합니다.

레퍼런스

외부 링크

• t-SNE를 사용한 데이터 시각화, t-SNE에 대한 Google Tech Talk
• 다양한 언어로 t-SNE 구현, Laurens van der Maatten이 관리하는 링크 컬렉션