Dyck

Dyck
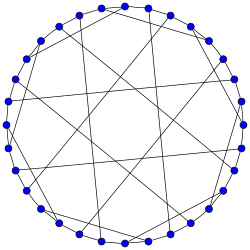Dyck 그래프
이름을 따서 명명됨	W. 다이크
정점	32
가장자리	48
반지름	5
지름	5
둘레	6
자동형성	192
색수	2
색도 지수	3
책두께	3
대기열 번호	2
특성.	대칭 큐빅 해밀턴어 양립자 케이리 그래프
그래프 및 모수 표

그래프 이론의 수학적 분야에서 Dyck 그래프는 월터 폰 다이크의 이름을 따서 32개의 정점과 48개의 가장자리를 가진 3개의 정규 그래프다.^[1][2]

120개의 뚜렷한 해밀턴 사이클을 가진 해밀턴이다.색도 2번, 색도 지수 3번, 반지름 5, 직경 5번, 둘레 6번을 가지고 있다.또한 3-Vertex 연결 그래프와 3-엣지 연결 그래프이기도 하다.책 두께 3과 줄 2가 있다.^[3]

Dyck 그래프는 토로이드 그래프이며, 대칭 토로이드 임베딩의 이중은 대칭과 해밀턴 둘 다에 강한 정규 그래프인 슈리칸데 그래프다.

대수적 특성

Dyck 그래프의 자동형성 그룹은 순서 192의 그룹이다.^[4]그것은 정점, 가장자리, 그리고 그래프의 호에서 전이적으로 작용한다.따라서 Dyck 그래프는 대칭 그래프다.그것은 어떤 정점과 어떤 가장자리로도 가져가는 자동모형을 가지고 있다.포스터 인구조사에 따르면, F32A로 참조되는 Dyck 그래프는 32 정점에 대한 유일한 입방 대칭 그래프다.^[5]

Dyck 그래프의 특성 ${\displaystyle \mathrm{다항식}}$은${\displaystyle }$( ${\displaystyle \mathrm{x}}$- 3${\displaystyle }$)${\displaystyle }$( ${\displaystyle {x\mathrm{}}^{}}$- ${\displaystyle 1{}^{}}$) ${\displaystyle {9\mathrm{}}^{}}$( ${\displaystyle x}$+ ${\displaystyle 1}$) (${\displaystyle }$x${\displaystyle 2{}^{}}$- ${\displaystyle 5{}^{}}$) ${\displaystyle {6\mathrm{}}^{}}$ ${\$)^{9}($x+1)^{9}(x^{2}-5)^{6$과 같다.

다이크 지도

Dyck 그래프는 Dyck 지도 또는 Dyck tiling으로 알려진 3x12 옥타곤 속 표면의 대칭 테셀레이션의 골격이다.이 타일링에 대한 이중 그래프는 완전한 삼분법 그래프 K이다_4,4,4.^[6][7]

갤러리

• 

  Dyck 그래프의 대체 도면.

• 

  Dyck 그래프의 색수는 2이다.

• 

  Dyck 그래프의 색지수는 3이다.

참조