일식 주기

일식은 특정 시간 간격으로 구분되어 반복적으로 발생할 수 있습니다. 이러한 간격을 일식 주기라고 합니다.^[1] 이러한 간격 중 하나의 반복에 의해 분리되는 일련의 일식을 일식 시리즈라고 합니다.

일식 조건

일식은 지구와 달이 태양과 일직선이 되고 태양에 의해 투영된 한 물체의 그림자가 다른 물체에 떨어질 때 발생할 수 있습니다. 그래서 달이 태양과 결합할 때, 달은 지구 표면의 좁은 지역에서 볼 때 태양 앞을 지나칠 수 있고 일식을 일으킬 수 있습니다. 보름달에 달이 태양과 반대일 때 달이 지구의 그림자를 통과할 수 있고, 지구의 밤반부에서 월식이 보입니다. 달의 결합과 반대는 특별한 이름을 가지고 있습니다: syzygy (그리스어로 "결합"을 뜻함) 이 달 단계의 중요성 때문입니다.

월식은 달이 태양 주위를 도는 지구 궤도의 평면(황도)에 대해 기울어져 있기 때문에 모든 달이나 보름달에 일어나는 것은 아닙니다. 따라서 지구에서 볼 때, 달이 태양에서 가장 가까운 곳에 나타나거나 달에서 가장 먼 곳에 나타날 때, 세 몸은 보통 정확히 같은 선상에 있지 않습니다.

이 기울기는 평균적으로 약 5° 9'로 태양의 겉보기 평균 직경(32' 2 ″), 달 바로 아래 지구 표면에서 볼 때 달(31' 37 ″), 달 거리에서 볼 때 지구 그림자(1° 23')보다 훨씬 큽니다.

따라서 대부분의 새로운 달에서는 지구가 달 그림자의 북쪽이나 남쪽을 너무 많이 지나가며, 대부분의 보름달에서는 달이 지구 그림자를 그리워합니다. 또한, 대부분의 일식에서 달의 겉보기 각지름은 달이 근일점 주위에 있지 않는 한, 즉 지구에 더 가깝고 평균보다 커 보이지 않는 한, 태양 원반을 완전히 가리기에는 충분하지 않습니다. 어쨌든 일식을 일으키기 위해서는 정렬이 거의 완벽해야 합니다.

일식은 달이 지구 궤도의 평면에 있거나 근처에 있을 때, 즉 황도 위도가 낮을 때에만 발생할 수 있습니다. 이것은 달이 황도에 있는 두 개의 궤도 마디 중 하나 주변에 있을 때 발생합니다. 물론 일식을 일으키기 위해서는, 그 때 태양이 한 마디 주변에 있어야 합니다. 일식과 같은 마디 또는 월식과 반대 마디입니다.

재발

일 년에 두 번, 태양이 달 궤도의 마디 근처에 있을 때 즈음에 일어나는 한 두 달의 기간인 일식 시즌 동안 최대 세 번의 일식이 일어날 수 있습니다.

일식이 일어난 지 한 달이 지나면 태양, 달, 지구의 상대적인 기하학적 구조가 바뀌기 때문에 월식이 매달 일어나는 것은 아닙니다.

지구에서 볼 때, 달이 마디로 돌아오는 데 걸리는 시간은 달이 태양과 같은 황도로 돌아오는 데 걸리는 시간보다 짧습니다. 그 주된 이유는 달이 지구 주위를 도는 궤도를 완성하는 시간 동안, 지구와 달은 대략 다음과 같이 완성되었기 때문입니다. 그들이 태양 주위를 도는 궤도의 ⁄13: 달이 다시 태양과 결합하거나 반대하기 위해서는 이것을 보충해야 합니다. 두 번째로, 달의 궤도 마디는 황도에서 서쪽으로 치우쳐 약 18.60년 만에 완전한 원을 완성하기 때문에, 드라코닉 월은 측면 달보다 짧습니다. 전체적으로, 시노딕 월과 드라코닉 월의 기간 차이는 거의 2+1 ⁄3일입니다. 마찬가지로, 지구에서 볼 수 있듯이, 태양은 황도 경로를 따라 이동할 때 양쪽 마디를 지나갑니다. 태양이 마디로 돌아오는 기간은 일식 또는 드라코닉 해라고 불리는데, 마디의 세차운동으로 인해 일 년에 비해 약 1 ⁄20년 짧은 약 346.6201일입니다.

만약 일식이 꼭 마디에 가까운 새로운 달에서 일어난다면, 다음 보름달에서 달은 이미 반대편 마디를 하루 이상 지나 지구의 그림자를 놓칠 수도 있고 놓칠 수도 있습니다. 다음 달이 되면 그것은 마디보다 훨씬 더 앞에 있기 때문에 지구 어딘가에서 일식이 일어날 가능성이 적습니다. 다음 달까지 행사는 분명히 없을 것입니다.

하지만, 약 5~6개월 후에 달은 반대쪽 마디에 가까이 떨어질 것입니다. 그 시기(반일식년)에는 태양도 반대쪽 마디로 이동할 것이므로, 상황은 다시 한 번 이상의 일식에 적합할 것입니다.

주기성

일식의 주기는 연속적인 두 일식 사이의 간격으로, 1개월, 5개월 또는 6개월입니다.^[2] 지구는 기원전 2000년에서 서기 3000년 사이에 총 11,898번의 일식을 경험할 것으로 계산됩니다. 특정 일식은 약 18년 후 11일과 8시간(6,585.32일)마다 반복되지만 동일한 지리적 지역에서는 반복되지 않습니다.^[3] 특정 지리적 지역은 54년 34일 주기로 특정 일식을 경험하게 됩니다.^[2] 개기일식은 지구 어딘가에서 평균 18개월마다 일어나지만,^[4]

일식의 반복

일식의 반복을 위해서는 지구, 달, 태양의 기하학적 정렬과 달 궤도의 일부 매개 변수가 반복되어야 합니다. 일식을 반복하려면 다음 파라미터와 기준을 반복해야 합니다.

1. 달은 새로운 단계에 있을 것입니다.
2. 근일점이나 달의 한 점의 경도는 같아야 합니다.
3. 오름차순 노드 또는 내림차순 노드의 경도는 같아야 합니다.
4. 지구는 태양으로부터 거의 같은 거리에 있을 것이고, 거의 같은 방향으로 기울어져 있을 것입니다.

이 조건들은 달의 궤도 운동의 세 시기, 즉, 대음월, 변칙월 및 드라코닉월과 관련이 있습니다. 다시 말해, 달이 대략 정수 개의 시노딕, 드라코닉, 변칙 기간(223, 242, 239)을 완료하고 지구-일월 기하학이 일식과 거의 동일할 때에만 특정 일식이 반복됩니다. 달은 지구로부터 같은 마디와 같은 거리에 있을 것입니다. 감마(일식 동안 달이 황도의 북쪽 또는 남쪽에 있는 거리)는 모든 사로스 시리즈에서 단조롭게 변화합니다. 감마선의 변화는 지구가 근일점 근처에 있을 때(12월~1월)보다 근일점 근처에 있을 때(6월~7월) 더 큽니다. 지구가 평균 거리(3~4월 또는 9~10월) 근처에 있을 때 감마의 변화는 평균적입니다.

월식의 반복

월식의 반복을 위해서는 달, 지구, 태양의 기하학적 정렬과 달 궤도의 일부 매개 변수가 반복되어야 합니다. 월식의 반복을 위해서는 다음 파라미터와 기준을 반복해야 합니다.

1. 달은 완전한 단계임에 틀림없습니다.
2. 근일점이나 달의 한 점의 경도는 같아야 합니다.
3. 오름차순 노드 또는 내림차순 노드의 경도는 같아야 합니다.
4. 지구는 태양으로부터 거의 같은 거리에 있을 것이고, 거의 같은 방향으로 기울어져 있을 것입니다.

이 조건들은 달의 궤도 운동의 세 시기, 즉, 대음월, 변칙월 및 드라코닉월과 관련이 있습니다. 다시 말해, 달이 대략 정수 개의 시노딕, 드라코닉, 변칙 기간(223, 242, 239)을 완료하고 지구-일월 기하학이 일식과 거의 동일할 때에만 특정 일식이 반복됩니다. 달은 지구로부터 같은 마디와 같은 거리에 있을 것입니다. 감마는 단일 사로스 시리즈 전반에 걸쳐 단조롭게 변화합니다. 감마선의 변화는 지구가 근일점 근처에 있을 때(12월~1월)보다 근일점 근처에 있을 때(6월~7월) 더 큽니다. 지구가 평균 거리(3~4월 또는 9~10월) 근처에 있을 때 감마의 변화는 평균적입니다.

월식은 발생하지 않습니다.

또 하나 고려해야 할 점은 달의 운동이 완벽한 원이 아니라는 것입니다. 궤도는 뚜렷하게 타원형이므로 지구로부터의 달 거리는 달 주기 내내 다양합니다. 이러한 다양한 거리는 달의 겉보기 지름을 변화시키기 때문에 일식의 발생 가능성, 지속 시간, 종류(부분, 고리, 전체, 혼합)에 영향을 미칩니다. 이 주기를 변칙적 달이라고 하며, 회음월과 함께 보름달의 시간과 출현에 약 14개의 달이 뜨는 소위 "보름달 주기"를 발생시킵니다. 달은 지구에 가까울 때(주변부 근처) 더 빠르게 움직이고, 포지 근처(가장 먼 거리)에 있을 때 더 느리게 움직이며, 따라서 주기적으로 양쪽에서 최대 14시간 정도의 시간이 변화하고, 달의 겉보기 각지름이 약 6% 증가하거나 감소합니다. 일식을 잘 예측하기 위해서는 일식 주기가 변칙 월수에 가까운 정수를 포함해야 합니다.

만약 지구가 태양을 중심으로 완벽한 원형 궤도를 가지고 있고, 달의 궤도 또한 완벽하게 원형이며 지구를 중심으로 하고, 두 궤도가 서로 동일 평면(같은 평면)에 있다면, 매달 두 번의 일식(29.53일)이 일어날 것입니다. 월식은 보름달 때마다, 일식은 초승달 때마다 일어나며, 일식은 모두 같은 종류가 될 것입니다. 사실 지구와 달 모두 타원 궤도를 가지고 있기 때문에 지구와 달 사이와 지구와 태양 사이의 거리가 다릅니다. 또한, 두 궤도 모두 같은 평면상에 있지 않습니다. 달의 궤도는 태양 주위를 도는 지구의 궤도와 약 5.14° 기울어져 있습니다. 그래서 달의 궤도는 황도를 두 지점 또는 마디로 가로지릅니다. 만약 달이 마디의 약 17° 이내에서 일어난다면, 지구의 어떤 곳에서 일식을 볼 수 있을 것입니다.^[5][6][7]

하루 평균 0.99°의 각속도로 태양은 각 마디를 중심으로 34° 폭의 일식대를 가로지르는데 34.5일이 걸립니다. 달의 태양에 대한 궤도의 평균 기간은 29.53일이기 때문에 태양이 결절일식 영역을 통과할 때 34.5일 간격으로 일식이 한 번씩 일어날 가능성이 있습니다. 이 기간을 일식 시즌이라고 합니다.^[2] 매 일식 시즌마다 두 번 또는 세 번의 일식이 일어납니다. 월식 기간 동안, 달의 궤도의 기울기는 낮으므로, 태양, 달, 그리고 지구는 일식이 일어나기에 충분히 직선으로 정렬됩니다.

수치

이는 위에서 설명한 다양한 유형의 달 길이입니다. (예: J2000.0 시대에 유효한 달의 에페메리스 ELP2000-85에 따르면, (예:)에서 가져온 것입니다.) 미어스 (1991):

SM = 29.53058853일 (음절월)

DM = 27.21 2220 817일 (드라코닉 월)

AM = 27.55454988일 (이상월)

EY = 346.620076일 (일식년)

태양, 달, 그리고 (올라가는) 마디의 세 가지 주요 이동점이 있다는 것을 주목하십시오. 그리고 세 쌍의 이동점이 각각 서로 만나는 세 가지 주요 기간이 있다는 것을 주목하십시오. 달이 태양으로 돌아오는 시노드 월, 달이 마디로 돌아오는 드라코 월, 그리고 태양이 노드로 돌아오는 일식의 해. 이 세 가지 양방향 관계는 독립적이지 않습니다(즉, 시노딕 월과 일식 년 모두 태양의 겉보기 운동에 의존하고, 드라코닉 월과 일식 년 모두 노드의 운동에 의존합니다). 실제로 일식 년은 시노딕 월과 드라코닉 월의 비트 기간으로 설명될 수 있습니다(즉, 일식 년은 시노딕 월과 드라코닉 월의 비트 기간으로 설명될 수 있습니다). 시노딕 월과 드라코닉 월의 차이의 기간), 공식:

${\displaystyle {\mbox}EY}}={\frac {{\mbox{SM}}\times{\mbox{DM}}{\mbox{SM}}-{\mbox{DM}}}}}$

위에 나열된 수치를 입력하면 확인할 수 있습니다.

일식 주기는 특정한 시노딕 월의 수가 드라코닉 월의 정수 또는 반 정수와 거의 같은 주기를 갖습니다: 일식 후에 한 번은 황도에서 달 궤도의 한 마디 근처에서 다시 신경질적인 현상(새달 또는 보름달)이 일어나고 일식이 다시 일어날 수 있습니다. 그러나, 시노딕 월과 드라코닉 월은 그들의 비율이 정수가 아니라는 점에서 부적절합니다. 우리는 이 비율을 일반적인 분수로 근사해야 합니다. 그런 다음 분자와 분모는 (약) 일식 주기를 나타내는 동일한 시간에 걸쳐 있는 두 기간의 배수인 드라코닉 월과 시노딕 월을 제공합니다.

이 분수들은 연속 분수의 방법에 의해 발견될 수 있습니다: 이 산술 기법은 적절한 분수에 의해 어떤 실제 숫자 값에 대한 일련의 더 나은 근사치를 제공합니다.

반 드라코닉 달마다 일식이 일어날 수 있기 때문에, 우리는 시노드 월마다 반 드라코닉 달의 수에 대한 근사치를 찾아야 합니다: 따라서 근사치에 대한 목표 비율은 SM / (DM/2) = 29.53058853 / (27.212220817/2) = 2.170391682입니다.

이 비율에 대한 연속 분수 팽창은 다음과 같습니다.

2.170391682 = [2;5,1,6,1,1,1,1,11,1...]: Quotients Convergents 반 DM/SM 십진법 이름 사이클(있는 경우) 2; 2/1 = 2 시노딕 달 5 11/5 = 2.2 pentalunex 1 13/6 = 2.16666667 학기 6 89/41 = 2.170731707 헵톤 1 102/47 = 2.170212766 옥톤 1 191/88 = 2.170454545 tzolkinex 1293/135 = 2.170370 트리토스 1484/223  = 2.170403587 사로스 1777/358 = 2.170391061 in 18253/3803 = 2.170391556 Uting cycle 11 9031/4161 = 2.170391732 선택비트 19808/4519 = 2.170391679 제곱년... 

반일식 년에 한 번 일어나는 시노드 월의 비율은 다음과 같습니다.

5.868831091 = [5;1,6,1,1,1,1,11,1...] 몫 수렴 SM/반 EY 십진법 SM/전체 EY 이름 사이클 5; 5/1 = 5 pentalunex 16/1 = 6 12/1학기 6 41/7 = 5.857142857 hepton 147/8 = 5.875 47/4 옥톤 188/15 = 5.866666667 tzolkinex 1 135/23 = 5.869565217 트리토스 1 223/38 = 5.868421053 223/19 사로스 1 358/61 = 5.868852459 716/61 in 1 3803/648 = 5.868846931 Utting cycle 11 4161/709 = 5.5.868829337 selebit 14519/770 = 5.868831169 4519/385 제곱년... 

이들 각각은 일식 주기입니다. 이들의 조합에 의해 덜 정확한 사이클이 구성될 수 있습니다.

일식 주기

이 표는 다양한 일식 주기의 특성을 요약한 것으로, 앞 단락들의 수치 결과로부터 계산될 수 있습니다; cf. Meeus (1997) Ch.9. 더 자세한 내용은 아래 주석에 나와 있으며 몇 가지 주목할 만한 사이클에는 자체 페이지가 있습니다. 많은 다른 사이클들이 주목을 받았는데, 그 중 일부는 이름이 붙여졌습니다.^[12]

어떤 일식 주기, 그리고 실제로 어떤 두 일식 사이의 간격은 사로스(s) 간격과 inex(i) 간격의 조합으로 표현될 수 있습니다. 이들은 "공식" 열에 나열되어 있습니다.

사이클	공식	날들	시노딕 몇달.	드라코닉 몇달.	변칙적 몇달.	이클립스 몇 해	열대 지방 몇 해	이클립스 계절들	노드
2주간	19i − 30+1⁄2s	14.77	0.5	0.543	0.536	0.043	0.040	0.086	교대하는
성대한 달	38i − 61s	29.53	1	1.085	1.072	0.085	0.081	0.17	저도.
음경의	53s − 33i	147.65	5	5.426	5.359	0.426	0.404	0.852	교대하는
학기	5i − 8s	177.18	6	6.511	6.430	0.511	0.485	1	교대하는
음력 해	10i − 16s	354.37	12	13.022	12.861	1.022	0.970	2	저도.
육각형의	13s - 8i	1,033.57	35	37.982	37.510	2.982	2.830	6	저도.
헵톤	5s − 3i	1,210.73	41	44.485	43.952	3.485	3.321	7	교대하는
옥톤의	2i − 3s	1,387.94	47	51.004	50.371	4.004	3.800	8	저도.
졸키넥스	2s − i	2,598.69	88	95.497	94.311	7.497	7.115	15	교대하는
히바르디나[12]	31s + 19i	3,277.90	111	119.975	120.457	9.457	8.975	19	교대하는
sar (하프 사로스)	1⁄2s	3,292.66	111.5	120.999	119.496	9.499	9.015	19	저도.
트리토스	이-스	3,986.63	135	146.501	144.681	11.501	10.915	23	교대하는
사로스	s	6,585.32	223	241.999	238.992	18.999	18.030	38	저도.
메토닉 사이클	10i − 15s	6,939.69	235	255.032	251.864	20.022	19.000	40	저도.
세마넥스[12]	3s - i	9,184,01	311	336.144	333.303	26.496	25.145	53	교대하는
6개의[12]	4i - 5s	9,361.20	317	342.629	339.733	27.007	25.145	54	저도.
인스펙스(i)	i	10,571.95	358	388.500	383.674	30.500	28.945	61	교대하는
비범한 사람들	3s	19,755.96	669	725.996	716.976	56.996	54.090	114	저도.
오브리 사이클[12]	i + ⁄2 1개	20,449.93	692.5	751.498	742.162	58.996	55.990	118	교대하는
유니도스[12]	i + 2s	23,742.59	804	872.497	861.658	68.497	65.005	137	교대하는
캘리픽 사이클	40i − 60s	27,758.76	940	1020.093	1007.420	80.085	76.000	160	저도.
삼합의	3i	31,715.85	1074	1165.500	1151.021	91.500	86.835	183	교대하는
팔멘 4분주기[12]	4i - 1s	35,702.48	1209	1417.266	1295.702	103.001	97.750	206	저도.
수은주[12] 사이클	2i + 3s	40,899.864	1385	1502.996	1484.323	117.996	111.980	236	저도.
트라이트릭스[12]	3i + 3s	51,471.815	1743	1891.496	1867.997	148.496	140.925	297	교대하는
데라 하이어 사이클[12]	6i	63,431.703	2148	2331.000	2302.410	183.000	173.670	366	저도.
삼육면체의[12]	3i + 6s	71,227.778	2412	2167.492	2584.973	205.492	195.015	411	교대하는
램버트 II 주기[12]	9i + s	101,732.876	3445	3738.500	3692.054	293.500	278.535	587	교대하는
맥도날드 사이클[12]	6i + 7s	109,528.951	3709	4024.991	3794.986	315.991	299.880	632	저도.
사용주기[12]	10i + s	112,304.826	3803	4127.000	4075.727	324.000	307.480	648	저도.
엄선된	11i + s	122,876.78	4161	4515.500	4459.401	354.499	336.425	709	교대하는
히파르키 사이클	25i − 21s	126,007.02	4267	4630.531	4573.002	363.531	344.996	727	교대하는
제곱년	12i + s	133,448.73	4519	4904.000	4843.074	384.999	365.371	770	저도.
그레고리아나[12]	6i + 11s	135,870.235	4601	4992.986	4930.955	391.986	372.000	784	저도.
육각형의[12]	6i + 12s	142,455.556	4824	5234.985	5169.947	410.985	390.030	822	저도.
그라탄 기네스 주기[12]	12i - 4s	142,809.923	4836	5248.007	5182.807	412.007	391.000	824	저도.
바빌로니아의	14i + 2s	161,177.95	5458	5922.999	5849.413	464.999	441.291	930	저도.
기본기	18i	190,295.109	6444	6993.001	6906.123	549.001	521.011	1098	저도.
샬레페[12]	18i + 2s	203,465.751	6,890	7476.999	7,384.107	586.999	557.071	1174	저도.
테트라디아 (Meus III)	22i − 4s	206,241.63	6984	7579.008	7484.849	595.008	564.671	1190	저도.
tetradia (Meeus I)	19i + 2s	214,037.70	7248	7865.500	7767.781	617.500	586.016	1235	교대하는
극고난도[12]	24i + 12s	332,750.665	11268	12227.987	12076.070	989.987	911.041	1920	저도.
카르투슈[12]	52i	549,741.426	18616	20202.006	19951.022	1586.006	1505.142	3172	저도.
팔레아호롤로지아[12]	55i + 3s	601,213.240	20359	22093.502	21819.0186	1734.502	1646.0673	3469	교대하는
하이브리디아[12]	55i + 4s	607,798.561	20582	22335.501	22058.0108	1753.501	1664.097	3507	교대하는
셀레노이드[12] 1	55i + 5s	614,383.883	20805	22577.499	22297.003	1772.499	1682.127	3545	교대하는
프록시마[12]	58i + 5s	646,099.734	21879	23743.000	23448.023	1864.000	1768.962	3728	저도.
헬리오트로프[12]	58i + 6s	652,685.055	22102	25923.158	23687.0155	1882.998	1786.992	3766	저도.
Megalosaros[12]	58i + 7s	659,270.376	22325	24226.997	23926.008	1901.997	1805.023	3804	저도.
이모빌리스[12]	58i + 8s	665,855.697	22548	24468.996	24165.000	1920.996	1823.052	3842	저도.
정확한[12] 시마	58i + 9s	672,441.019	22771	24710.994	24403.992	1939.994	1841.083	3880	교대하는
맥케이 사이클[12]	76i + 9s	1,076,773.829	29215	31703.996	31,310.115	2488.996	2362.093	4978	교대하는
셀레노이드[12] 2	95i+11s	1,076,773.829	36463	39569.496	39077.896	3106.496	2948.109	6213	교대하는
호롤로지아[12]	110i + 7s	1,209,011.802	40941	44429.003	43877.029	3488.003	3310.164	6976	저도.

메모들

2주

한 달 반(29.53일). 일식이 있을 때, 다음 번에 또 다른 일식이 일어날 가능성이 꽤 있습니다: 태양과 달은 마디에 대해 15° 정도 움직였을 것이지만(달은 이전에 있었던 곳과 반대이지만), 광도는 여전히 일식을 만들기에 한계 내에 있을 수 있습니다. 예를 들어, 2002년 5월 26일의 반월식은 2002년 6월 10일의 금환일식과 6월 24일의 반월식이 뒤따릅니다. 초승달과 보름달 사이의 가장 짧은 달의 2주는 약 13일과 21.5시간 동안 지속되는 반면, 가장 긴 달의 2주는 약 15일과 14.5시간 동안 지속됩니다. (이색 때문에, 이 값들은 4분의 1달마다 다릅니다. 1/4분기 달과 마지막 4분기 달 사이의 가장 짧은 달 2주는 13일 12시간 정도밖에 지속되지 않는 반면, 가장 긴 달은 16일 2시간 정도 지속됩니다.)

자세한 내용은 일식 시즌을 참조하십시오.

성음월

마찬가지로, 한 달 간격으로 발생하는 두 사건은 29° 간격으로 노드 양쪽의 두 위치에 태양과 달이 있습니다. 둘 다 부분일식을 일으킬 수 있습니다. 월식의 경우, 그것은 반월식입니다.

펜탈루넥스

5개월. 연속적인 일식이나 월식은 1개월, 5개월 또는 6개월 간격으로 발생할 수 있습니다.^[13]

학기

반년. 일식은 8번의 일식이 지속되는 주기로 교대 마디에서 정확히 한 학기 간격으로 반복됩니다. 변칙, 극월, 열대년의 반 정수에 가깝기 때문에, 각 일식은 (일반적으로) 매 학기 반구와 전체와 고리 사이에서 번갈아 가며 일어날 것입니다. 따라서 일반적으로 주어진 음력 해에는 개기일식 또는 금환일식이 각각 최대 한 번씩 발생합니다. (단, 8학기 급수의 중간에는 반구가 전환되며, 급수 중에는 홀수와 짝수 중 어느 것이 합계인지에 대한 전환이 있습니다.) 월식의 경우, 월식은 8번의 월식이 지속되는 주기로 교대하는 마디에서 정확히 한 학기 간격으로 반복됩니다. 월식은 변칙적, 극월적, 열대년의 반 정수에 가깝기 때문에 일반적으로 매 학기 지구 그림자의 가장자리를 번갈아 가며, 달의 반음영과 우산 그림자 차이가 1보다 작거나 큰 월식을 번갈아 가며 볼 수 있습니다. 따라서 달의 반음영과 우산 그림자 차이가 각각 1보다 작거나 큰 최대 1개의 월식이 있습니다.

음력

일식 해보다 약간 긴 12개월: 태양이 마디로 돌아갔기 때문에 일식이 다시 일어날 수 있습니다.

헥손

6번의 일식 계절과 상당히 짧은 일식 주기입니다. 헥손 시리즈의 각 일식은 (마지막을 제외하고) 사로스 시리즈 번호가 8보다 낮은 일식에 이어 항상 같은 노드에서 발생합니다. 이는 35개의 시노딕 월에 해당하며, 1개는 달의 3년(36개의 시노딕 월)보다 작습니다. 언제든지 6개의 헥손 시리즈가 활성화됩니다.

헵톤

7개의 일식 계절과 덜 주목할 만한 일식 주기 중 하나입니다. 헵톤의 각 일식은 이전에 항상 교대 노드에서 발생하는 일식 3 사로스 시리즈에 이어집니다. 이는 41개의 시노딕 월에 해당합니다. 간격은 거의 전체 주수(172.96)이므로 각 월식은 일반적으로 한 주 동안 같은 요일에 수행됩니다(평균 4분의 1일 정도 불규칙적으로 뒤로 이동). 언제든지 7개의 헵톤 시리즈가 활성화됩니다.

옥톤

8번의 일식 계절, 1번의 메토닉 사이클, 1번의 ⁄ 5번의 짧은 일식 주기, 그리고 꽤 괜찮은 짧은 일식 주기를 갖지만, 변칙적인 결과는 좋지 않습니다. 직렬의 각 옥톤은 2개의 사로 떨어져 있으며 항상 같은 노드에서 발생합니다. 47개의 시노딕 월과 같습니다. 언제든지 8개의 옥톤 시리즈가 활성화됩니다.

졸키넥스

반 드라코닉 월을 포함하므로 교대 노드 및 반구 사이에서 교대로 발생합니다. 각각의 연속적인 일식은 이전의 것으로부터 이전의 사로스 시리즈의 일원입니다. 거의 10개의 졸킨과 맞먹습니다. 직렬의 모든 3분의 1 tzolkinex는 변칙 월의 정수에 가깝기 때문에 유사한 특성을 갖습니다.

히바르디나

시리즈의 수명이 짧은 일식 주기(3개의 일식으로 구성됨). 1개의 LUN을 추가하면 동일한 상황을 따르는 또 다른 사이클이 생성됩니다. 두 사이클 모두 sar(반사로스)를 둘러싸고 있습니다.^[14]

Sar(하프 사로스)

홀수 2주(223)를 포함합니다. 따라서 월식은 각 주기마다 월식과 태양식을 번갈아 가며 같은 마디에서 비슷한 특징을 가지고 발생합니다. 작은 감마가 있는 일식은 매우 중심이 되는 개기월식이 뒤따를 것입니다. 달의 페넘브라가 지구의 남쪽 사지를 겨우 스치는 일식은 반 사로스 후에 달이 지구의 페넘브라의 남쪽 사지를 스치는 월식이 뒤따를 것입니다.^[15]

트리토스

평범한 주기로, inex - saros와 같습니다. 삼중 삼중항은 변칙 월의 정수에 가깝기 때문에 유사한 특성을 갖습니다.

사로스

가장 잘 알려진 일식 주기이며, 223개의 시노딕 월이 242개의 드라코닉 월과 51분의 오차로 동일한 일식을 예측하는 데 가장 적합한 주기 중 하나입니다. 그것은 또한 239개의 변칙적인 달에 매우 가까워서, 하나의 사로 사이의 두 개의 일식 사이의 상황을 매우 비슷하게 만듭니다. 전체 일수보다 하루의 3분의 1이 더 많은 일식은 지구에서 약 120° 더 서쪽으로 치우쳐 있습니다.

경운기 또는 자궁근종

거의 6940일로 정의되는 이 날은 365+1 ⁄4일의 19년에 걸쳐 단 몇 시간에 불과하며 235개의 시노드 월이지만, 또한 5개의 옥톤(octon) 주기이며 20개의 일식 년에 가깝기 때문에 동일한 달력 날짜 또는 2개의 달력 날짜에 4개 또는 5개의 일식이 발생합니다. 29일의 110 "공허월"과 30일의 125 "풀월"에 해당합니다.

세마넥스

정수 주수를 달성한다는 점에서 매우 정확합니다. 이 기간의 각 일식은 항상 교대 노드에서 발생하는 이전의 사로스 시리즈의 구성원입니다. 이는 25년 1개월 14일 또는 311번의 윤회와 같습니다.^[12]

칙스

약 36 tzolk'in의 일식 주기입니다. 이 기간의 각 일식은 4개의 사로스 계열로 나뉘며 항상 같은 노드에서 발생합니다. 이는 25년 6개월 18일 또는 317번의 윤회와 같습니다.^[12]

인스

일식 주기 분류에 매우 편리합니다. 일식 후에 또 다른 일식은 거의 같은 경도에서 일어나지만 위도는 반대입니다. 인스 시리즈는 스퍼트가 시작된 후 수천 년 동안 계속되어 29년에서 20일 간격으로 일식이 발생합니다. 인시사이클은 지속되는 동안 가장 많은 수의 일식을 일으키는 사이클입니다. 인스 시리즈 30은 사로스 시리즈 -245 (기원전 9435년)에서 처음으로 일식을 일으켰고, 사로스 시리즈 -197 (기원전 8045년) 이후 29년마다 일식을 만들어 왔으며, 서기 15,000년 훨씬 지난 시점까지 707번의 ^[16]연속 일식을 만들어낼 것입니다. 이 이름은 1951년 조지 반 덴 버그에 의해 소개되었습니다.^[12]

엑셀리그모스

세 개의 사로는 거의 정수 일수를 가지고 있어서 다음 일식은 한 개의 사로에서 발생한 일식보다 약 8시간 늦게 또는 한 개의 사로에서 발생한 일식에서 서쪽으로 약 120° 떨어진 곳에서 볼 수 있다는 장점이 있습니다.

오브리 사이클

스톤헨지에 위치한 오브리 홀스로 측정한 일식 계산에서 이름을 따왔습니다. 월식은 1385주로, 56년 만에 달과 태양이 번갈아 가며 -3.5일.^[12]

유니도스

65년에 아주 가깝습니다. 67년은 음력이고 65년은 겨우 1.3일 차이로 넘습니다. 칼 팔멘이 제안한 이름은 2개의 사로가 인젝스 위에 추가된다는 것입니다.^[12]

캘리픽 사이클

940개의 시노딕 월(synodic months), 즉 441개의 중공 월(hollow months)과 499개의 전체 월(full months)에 해당하며, 따라서 4개의 메토닉 사이클(Metonic cycle)에서 하루를 뺀 값 또는 정확히는 이는 940번의 실행 중 오류가 5.9시간에 불과합니다. 이 주기는 예를 들어 부활절 날짜를 계산할 때 유용하기는 하지만, 기껏해야 두 번의 일식(둘 다 부분적)과 기껏해야 두 번의 월식(둘 다 반월식)을 일으킬 수 있습니다. 캘리픽의 주기는 20옥톤이고, 일련의 옥톤들은 종종 21개의 일식만을 만들어내기 때문에, 그러한 일련의 첫 번째와 마지막만이 캘리픽 주기에 의해 분리됩니다. 대부분의 일식은 940번의 월식이 뒤따르는 것이 아니라 939번의 월식(두 번의 인스펙스와 사로스)이 뒤따르며, 이는 유사한 월식을 만들어냅니다.^[12]

트라이어드

3배의 ix는 거의 정수 개의 변칙적인 달을 가지고 있다는 장점을 가지고 있습니다. 이는 두 개의 일식 사이의 상황을 하나의 삼합식과 매우 유사하지만 반대 위도에 있습니다. 거의 정확하게 87년에서 2개월을 뺀 것입니다. 삼합은 모든 세 번째 사로스 시리즈가 비슷하다는 것을 의미합니다(예를 들어, 중앙식은 대부분 개기일식 또는 대부분 고리일식). 예를 들어 사로스 130, 133, 136, 139, 142, 145는 모두 주로 개기일식을 일으킵니다.

팔멘 4분주기

4inex에서 사로스를 뺀다는 점에서 칼 팔멘의 이름을 따왔습니다. 각각의 일식은 나중에 같은 노드에서 항상 발생하는 4개의 사로스 시리즈로 이어집니다. 97년 9개월 또는 1209개월의 윤회와 같습니다.^[12]

수은주 사이클

이는 수성의 약 353개의 시노드 주기와 동일하므로,^[17] 각 주기 동안 수성이 궤도에 위치하는 시점과 일치하며, 이는 112년에서 1주일 또는 1385개의 달을 뺀 시간과 동일합니다.^[12]

트리트릭스

이는 3개의 saros를 더한 3개의 saros와 동일하며, 140년 11개월 또는 1743년의 윤년으로 항상 교대 노드에서 발생합니다.^[12]

데라 하이어 사이클

1687년 필립 드 라 하이어가 자신의 타뷸라룸 천문대에서 채택한 육쌍둥이. 173년 8개월 3일 또는 2148년 달은 173년 8개월 3일이며, 179년 음력과 같고, 항상 같은 노드에서 발생하며, 2개의 삼분의 삼분의 삼분의 삼분의 삼분의 삼분의 삼분의 삼분의 삼분의 일이기 때문에 항상 같은 노드에서 발생합니다.^[12]

트리헥스

3개의 사로에 6개의 사로를 더한 값으로 195년 동안 6일 동안 지속되거나 2412번의 달이 지속되며 201개의 달이 항상 교대 노드에서 발생합니다.^[12]

램버트 II 주기

거의 정수 개의 변칙 월수가 달성됨에 따라 유사한 상황에서 일식이 발생하는 일식 주기입니다. 이는 278년 6개월 15일 또는 3445번의 윤회와 같습니다.^[12]

맥도날드 사이클

월식 주기는 299년 11개월에서 12일 또는 3709개월을 뺀 것과 같습니다. 이는 299년 10개월 18일 또는 3709번의 런닝과 동일하며 항상 동일한 노드에서 발생합니다.^[12]

사용주기

일식년과 유성월의 비율 사이의 지속적인 분수 발달에서 일곱 번째 수렴. 이는 307년 6개월에서 5일 또는 3803번의 회전을 뺀 것과 같으며, 이러한 시리즈의 기대 수명은 137,000년 이상입니다. 1827년 James Uting에 의해 처음 논의되었습니다.^[12]

셀레빗

월식 년수(354.5)가 음력 1년(354.371)의 일수(우연)와 거의 일치하는 월식 주기입니다. 이는 약 336년 5개월 6일 또는 4161번의 윤회와 같습니다. 그것은 일식 년과 일식 월 사이의 비율의 지속적인 분수 발달의 수렴이며, 수천 년의 수명과 별개로 일련의 일식을 제공합니다.

히파르키 사이클

주목할 만한 일식 주기는 아니지만, 히파르코스는 회음절 및 변칙 월, 연도(345년) 및 일의 정수 수와 일치하도록 그것을 구성했습니다. 그는 자신의 일식 관측과 345년 전 바빌론 기록을 비교함으로써 칼데아인들이 사용했던 다양한 기간의 정확성을 검증할 수 있었습니다.

제곱년

태양년(365.371)의 수가 1태양년(365.242)의 일수와 밀접하게 일치하는 일식 주기. 365년 4.5개월 또는 4519번의 윤회가 지속됩니다. 일식년과 일식월 사이의 비율의 지속적인 분수 개발에서 8번째 수렴이며, 1 제곱년 간격의 일식은 수천 년의 기대 수명을 제공합니다. 우리 시대의 많은 일식들은 13,000년 이상 지속되어 온 "평방년" 시리즈 또는 셀레비트 시리즈에 속하며, 많은 일식들은 13,000년 이상 지속될 것입니다.^[16] 제곱년 시리즈만 해도 처음부터 끝까지 총 500만 년 이상이 될 수 있습니다.^[12]

그레고리아나

한 주와 그레고리력의 동일한 날을 향해 돌아오는 것으로 유명하며, 이 기간은 372년 또는 4601번의 윤년으로 항상 같은 노드에서 발생하기 때문에 대략 정수의 연도, 월, 주, 일을 달성합니다.^[12][18]

헥스도데카

6inx + 12 saros로 390년 + 12일 또는 4824번의 달은 402년으로 항상 같은 노드에서 발생합니다. 루니솔라 접합부의 타이밍을 정확하게 계산하는 데 유용합니다.^[12]

그라탄 기네스 주기

그레고리안력과 음력 모두에서 일식을 계산하는 가장 짧은 주기입니다. 391년 또는 4836년, 즉 403년의 달과 같습니다. 헨리 그라탄 기네스가 발견했습니다.^[19][12]

바빌로니아의

칼데아인들은 5458개월 만에 위도로 돌아오는 비율 5923을 천문학 계산에 사용했습니다.

기본기

거의 정수에 가까운 달력 년수(521년 + 4일), 변칙 년수(521년 - 5일) 및 주수(521년 - 5일)를 달성합니다. 이는 음력 537년인 644개의 달수와 일치하므로 율리우스력과 주수가 같은 날에 일식으로 이어집니다. 랄랑드(Astronomie, 3th Ed., vol.)에 따르면. II, 195) 기본기는 A.G. Pingré에 의해 처음 발견되었습니다. 그것은 A에서도 언급되었습니다. 맥케이와 몽크(1902), 슈레이더(1913), 알렉산더 포고(1935)에 의해 재발견되었습니다. Torroja Menendez(1941)와 Barlow et al.(1944)에서도 Van den Bergh와 함께 언급되었습니다.^[12]

샬레페

18inx + 2 saros와 같으며, 따라서 557년 1개월에서 3일 또는 6890번의 달은 거의 정수의 변칙적인 달에서 발생합니다.^[12]

테트라디아

가끔 6개의 달(한 학기) 간격을 두고 4개의 개기월식이 연속적으로 일어나는데, 이것을 테트라라고 합니다. 지오반니 시아파렐리(Giovanni Schiaparelli)는 이러한 테트라드가 희귀한 시대에 의해 중단되어 비교적 자주 발생하는 시대가 있다는 것을 알아차렸습니다. 이 변형은 약 6세기가 걸립니다. 안토니 파네코크(Antonie Panneekoek, 1951)는 이 현상에 대한 설명을 제공했고 591년의 기간을 발견했습니다. Theodor von Opolzer의 Canon der Finsternisse의 Van den Bergh (1954)는 586년의 기간을 발견했습니다. 이것은 마침 일식 주기입니다. Meeus [I] (1997)를 참조하십시오. 이 현상은 아래에서 설명하는 것처럼 지구의 타원 궤도와 관련이 있습니다. 최근 튜더 휴즈(Tudor Hughes)는 지구 궤도의 이심률의 세속적인 변화로 인해 테트라드의 발생 기간이 가변적이며, 현재 약 565년이라고 설명했습니다. 자세한 논의는 Meeus III(2004)를 참조하십시오.

하이퍼엑셀리그모스

캘리픽 주기가 12에서 1을 뺀 것과 같으므로 911년에 15일 또는 11268년(939년)입니다. 비록 939개의 달이 떨어져 있는 일식은 (거의 정수개의 드라코닉 달이 달성됨에 따라) 비슷한 성격을 가지고 있지만, 12개의 그러한 기간은 상당한 변화를 보여줍니다.^[12]

카르투슈

52inex와 같으며, 따라서 1505년 1개월 23일 또는 18616년의 윤년입니다. 이 기간의 일식은 거의 정수 개의 변칙 월이 달성되는 것과 비슷한 거리에서 발생합니다.^[12]

팔레아호롤로지아

55에 사로 3을 더한 것과 같으며, 1646년 24일 또는 20359번의 윤년입니다. 일식의 타이밍을 계산하는 데 유용합니다.^[12]

하이브리디아

55inx에 4개의 사로를 더하면 1664년 1개월 5일 또는 20582년의 달은 정수개의 변칙적인 달에 가깝기 때문에 유사한 특성을 갖지만 반대 위도에 있습니다.^[12]

셀레노이드

서기 3천 년 동안 일식의 크기를 계산하는 데 유용한 일식 주기의 이름입니다. 조지 반 덴 버그(George van den Bergh)는 1951년 95개의 95개의 95개의 95개의 10개의 사로(2948년 1개월 9일 또는 36463개의 1개월)를 언급하기 전에 55개의 사로와 5개의 사로(1682년 1개월 17일 또는 20805개의 달)의 기간을 처음 언급했습니다.^[12]

프록시마

58 inexe + 5 saros와 같고 거의 2485 tzolkins이므로 1769년에서 15일 또는 21879년의 달을 뺀 값으로 항상 동일한 노드에서 발생하고 일정한 수의 드라코닉 및 변칙 월 및 주를 향해 발생하므로 각 일식의 상황은 성격 및 주간 반환과 같은 근접한 거리에 있습니다.^[12]

헬리오트로프

이는 58 inx 6 saros를 더한 값이므로 1787년에서 3일 또는 22102년 달을 뺀 값이므로 정수 년에 가까운 지구 표면의 일식 중심선의 종방향 위치를 계산하는 데 유용합니다.^[12]

Megalosaros

58inex + 7 saros는 95개의 메토닉 사이클이므로 1805년 + 8일 또는 22325번의 달은 항상 동일한 노드에서 발생하며 95번의 반복이 불일치를 크게 축적하기 때문에 19년부터 메토닉 사이클의 불일치를 나타냅니다. 이는 100개의 사로스 주기가 사로스 시리즈의 수명을 초과하기 때문에 100개의 사로스 주기 간격(단 25개의 달에 의해 그 값을 초과함)의 일식 기간에 비교적 가까운 근사치입니다.^[12][20]

이모빌리스

이는 1879년 음력으로 1823년에 19일 또는 22548년에 달하며, 항상 같은 노드에서 발생하는 58개의 인시온과 8개의 사로스를 더한 값입니다.^[12]

아큐라티시마

58개의 사로에 9개의 사로를 더하면 1841년 1개월 또는 22771개의 달이 되는데, 이는 대략 정수 주수이기 때문에 한 주의 같은 날에 일식이 일어날 수 있습니다. 일식의 크기와 특성을 계산하는 데에도 유용합니다.^[12]

맥케이 사이클

76에 9개의 사로를 더한 것과 같으며, 따라서 2362년 1개월 4일 또는 29215번의 달은 항상 동일한 노드에서 발생합니다. A가 언급했습니다. 1800년대의 매케이.^[12]

호롤로지아

110 inx에 7 saros를 더하면 3,310년 2개월 4일 또는 40941번의 런닝이 항상 동일한 노드에서 발생합니다. 일식의 시간과 크기를 계산하는 데 유용합니다. 일식은 대략 극과 극의 달과 주의 정수개의 간격을 가지며, 특성과 주의 시간에서 유사한 일식으로 이어지기 때문입니다.^[12]

사로스 시리즈와 인엑스 시리즈

모든 일식은 주어진 사로스 시리즈와 inex 시리즈에 할당될 수 있습니다. 일식이 일어나는 해는 대략 다음과 같습니다.^[21]

year = 28.945 × 사로스계열 번호 + 18.030 × inex계열 번호 - 2882.55

이것이 1보다 크면 정수 부분은 AD년을 주지만 음수일 때는 정수 부분을 취하고 2를 더하면 BC가 얻어집니다. 예를 들어, 사로스 시리즈 0과 인스 시리즈 0에서의 일식은 기원전 2884년 중반이었습니다. Luca Quaglia와 John Tilley는 기원전 11001년부터 서기 15000년까지 61775번의 일식을 보여주는 사로스와 인엑스에 의해 배열된 일식의 "파노라마"를 만들어냈습니다 (아래 참조).^[22] 그래프의 각 열은 부분일식에서 개기일식 또는 환상일식으로 그리고 다시 부분일식으로 매끄럽게 진행되는 완전한 사로스 계열입니다. 각 그래프 행은 inex 시리즈를 나타냅니다. 223개의 대음절 달 중 사로스는 드라코닉 달의 전체 수보다 약간 적기 때문에, 사로스 시리즈의 초기 일식은 달이 드라코닉 달의 시작과 끝을 통과한 후에 일어나는 반면, 후기 일식은 달이 드라코닉 달의 시작과 끝을 통과하기 전에 발생합니다. 18년마다 평균적으로 노드에 대해 서쪽으로 약 0.5도 더 먼 곳에서 일식이 발생하지만 진행은 균일하지 않습니다.

일식은 –11000에서 +15000까지.

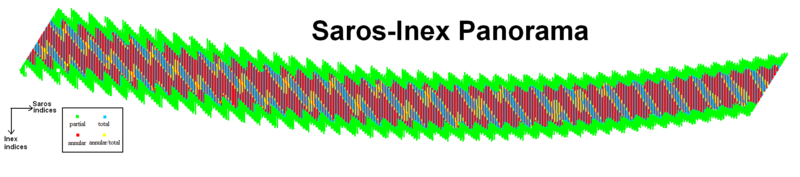사로스와 숫자는 주어진 날짜 근처의 일식에 대해 계산할 수 있습니다.

사로스와 숫자는 또한 월식에 대해 정의됩니다. 주어진 사로스와 인젝스 시리즈의 일식은 사로스 수가 26보다 낮고 인젝스 수가 18보다 높은 월식에 의해 2주 전에 선행되거나, 사로스 수가 12보다 높고 인젝스 수가 43보다 낮은 월식에 의해 2주 후에 후속될 것입니다. 일식과 마찬가지로 그레고리안의 월식은 다음과 같이 계산할 수 있습니다.

year = 28.945 × 사로스계열 번호 + 18.030 × inex계열 번호 - 2454.564

월식도 유사한 도표로 표시할 수 있는데, 이 도표는 서기 1000년에서 2500년을 대상으로 합니다. 노란색 대각선 띠는 1900년부터 2100년까지의 모든 일식을 나타냅니다. 이 그래프는 1900-2100년 기간에 인접한 다른 세기에 비해 평균 이상의 개기월식 수가 포함되어 있음을 즉시 보여줍니다.

이것은 테트라드가 다른 시기보다 현재 더 흔하다는 사실과 관련이 있습니다. 테트라드는 4개의 월식이 4개의 달의 정수에서 발생할 때 발생하며, 8개(한 학기 간격) 감소하여 상당히 중심적인 월식(작은 감마)을 제공하며, 더욱이 월식은 지구 근일점과 근일점의 중간쯤에서 발생합니다. 예를 들어, 2014-2015년의 테트라드(일명 네 개의 블러드 문)에서, 난수는 52, 44, 36, 28이었고, 일식은 4월과 9월 말에서 10월 초에 발생했습니다. 일반적으로 감마의 절대값은 감소하다가 증가하지만, 4월에는 태양이 평균경도보다 더 동쪽에 있고, 9/10월에는 평균경도보다 더 서쪽에 있기 때문에 첫 번째와 네 번째 일식에서 감마의 절대값은 감소하는 반면 두 번째와 세 번째에서는 절대값이 증가합니다. 그 결과 네 개의 감마값 모두 개기월식으로 이어질 만큼 작다는 결과가 나왔습니다. 달이 보통 평균 경도에 있지 않은 태양(또는 태양 반대 지점)과 "따라잡는" 현상은 "스턴 체이스"라고 불립니다.^[23]

인스 시리즈는 1년 동안 천천히 움직이며, 각각의 일식은 29년 후인 1년에 약 20일 먼저 발생합니다. 이는 18.2 주기(526년) 동안 날짜가 1년 내내 움직인다는 것을 의미합니다. 하지만 지구 궤도의 근일점도 서서히 움직이고 있기 때문에, 현재 테트라드를 생성하고 있는 inex 시리즈는 약 586년 후에 다시 지구 근일점과 근일점의 중간에 있게 될 것입니다.^[24]

어떤 사람은 x축이 1년 중 시간을 나타내도록 일식이나 월식에 대해 inex 대 saros의 그래프를 왜곡할 수 있습니다. (다른 사람보다 두 개의 saros 계열과 하나의 inex 계열이 늦은 일식은 1년 중에 겨우 1.8일 늦게 일어날 것입니다.) 이것은 586년의 진동을 근일점을 중심으로 상승하고 원일점을 중심으로 하강하는 진동으로 보여줍니다.

참고 항목

• 사로스 (천문학)

참고문헌

• S. 뉴컴(1882): 일식이 재발하는 것에 대해. 천문학자.파프.암.에브. vol. 딱. I. 1882년 워싱턴 해군 항해국
• J.N. Stockwell (1901): 일식-주기. 천문학자.J. 504 [vol.xx1(24)], 14-Aug-1901
• A.C.D. Crommelin (1901): 29년의 일식 주기. 천문대 xxiv nr.310, 379, Oct-1901
• A. Pannekoek (1951): 월식의 주기성. 콘 네드 프로님 카드. 긴장합니다. Ser.B vol.54 pp. 30..41 (1951)
• G. van den Bergh (1954): 기원전 2천년의 일식. Tjeenk Willink & Zn NV, Haarlem 1954
• G. van den Bergh (1955): 태양식(및 월식)의 주기와 변화, 2권. Tjeenk Willink & Zn NV, Haarlem 1955
• 장 미우스 (1991): 천문 알고리즘 (1sted). Willmann-Bell, Richmond VA 1991; ISBN 0-943396-35-2
• 장 미어스(Jean Meeus) (1997): 수학 천문학 모렐스 [I], Ch. 9 일식: 일부 주기율(49...55쪽). Willmann-Bell, Richmond VA 1997; ISBN 0-943396-51-4
• 장 미우스(2004): 수리천문학 Morlels III, Ch. 21 Lunar Tetrads (123..140쪽). Willmann-Bell, Richmond VA 2004; ISBN 0-943396-81-6

외부 링크

• 일식 주기 카탈로그(위의 내용보다 포괄적)
• 기원전 2000년에서 서기 3000년 사이의 5,000년 가치의 일식을 조사합니다.
• 일식, 고대인들의 우주 시계
• 사로스와 인젝스