달 거리(천문)

Lunar distance (astronomy)
달 거리
Lunar perigee apogee.png
달 거리인 384,399 km는 달에서 지구까지의 평균 거리이다.실제 거리는 공전 궤도에 따라 달라집니다.이 이미지는 달이 지구에서 가장 가깝고 멀리 있을 때 달의 겉보기 크기를 비교한다.
일반 정보
단위계천문학
단위거리
기호.LD 또는 L { \ _ { \ L}
변환
LD×1......와 같다
SI 베이스 유닛 384399×103 m
미터법 384399km
영어 단위 238854 mi
천문 단위 0.002569 au

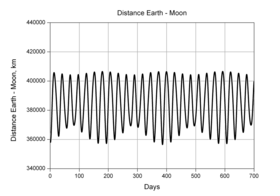
순간 지구-달 거리 또는 달까지의 거리는 지구의 중심에서 달의 중심까지의 거리입니다.달 거리(LD 또는 L { _L}})는 천문학에서 측정 단위이다.더 엄밀히 말하면, 이것은 지구 중심 달 궤도의 반장축이다.달의 거리는 약 400,000km, 즉 1.28광초이다. 이는 지구 지름의 약 30배이다.달 거리 400보다 조금 작은 것이 천문 단위를 구성합니다.

준장축의 값은 384,399km(238,854mi)[1][2]입니다.지구와 달 사이의 시간 평균 거리는 385,000.6km이다.실제 거리는 달의 궤도 궤도에 따라 변하며, 근지점에서 356,500km(221,500mi)에서 원지점에서 406,700km(252,700mi)까지 다양하며, 그 결과 50,200km(31,200mi)[3]의 차이가 난다.

달거리는 일반적으로 지구 근접 물체와의 [4]거리를 나타내기 위해 사용됩니다.달 반장축은 중요한 천문학적 기준입니다. 몇 밀리미터의 정밀도는 반장축을 몇 데시미터까지 결정합니다. 이것은 일반 상대성 [5]이론과 같은 중력 이론의 테스트와 지구의 [8]질량,[6] 반지름,[7] 회전과 같은 다른 천문학적인 값들을 정제하는 데 영향을 미칩니다.이 측정은 태양의 질량과 거리뿐만 아니라 달의 반지름을 특징짓는 데도 유용합니다.

달거리의 밀리미터 정밀 측정은 레이저 광선이 지구의 관측소와 달에 있는 역반사체 사이를 이동하는 데 걸리는 시간을 측정하여 이루어집니다.달은 달 레이저 거리 측정 실험에서 [9][10][11]검출된 바와 같이 매년 평균 3.8cm의 속도로 지구로부터 멀어지고 있다.

가치

지구와 달 사이의 거리(평균값) – 크기 및 측정할 거리.
OSIRIS-REXprobe가 촬영한 지구와 달의 사진
선택한 단위로 표현된 달 거리
구성 단위 평균값 불확실성 참조
미터링 3.84399×108 1.1mm [1]
킬로미터 384,399 1.1mm [1]
마일 238,854 0.043인치 [1]
지구 반지름 60.32 [12]
AU 1/388.6 = 0.00257 [13][14]
광초 1.282 37.5×10−12 [1]
  • AU는 389 달 [15]거리입니다.
  • 1광년은 24,611,700 달의 [15][16]거리이다.
  • 정지 지구 궤도는 지구 중심에서 42,199 km(26,199 mi) 떨어져 있습니다. 즉, 1/9.19 LD = 0.10968 LD입니다.

변화

달의 순간 거리는 끊임없이 변화하고 있다.실제로 달과 지구 사이의 실제 거리는 비원형 [17]궤도로 인해 [3]초속 75미터, 즉 단 6시간 만에 1,000킬로미터(620 mi) 이상 빠르게 변할 수 있다.달 거리에도 영향을 미치는 다른 효과들이 있다.이 섹션에서는 몇 가지 요인에 대해 설명합니다.

지구 표면에서 본 각지름으로 지구에서 달의 최소, 평균 및 최대 거리 측정

섭동 및 편심

달까지의 거리는 1시간의 샘플링 [18]기간에 걸쳐 2mm의 정확도로 측정할 수 있으며, 이는 반장축에 대한 데시미터의 전체적인 불확실성을 초래한다.그러나 이심률이 다양한 타원형 궤도로 인해 순간 거리는 월 주기에 따라 달라집니다.게다가, 거리는 다양한 천체들의 중력 효과에 의해 교란됩니다 – 가장 중요한 것은 태양이고 금성과 목성은 덜합니다.미세한 섭동을 일으키는 다른 힘으로는 태양계의 다른 행성과 소행성에 대한 중력, 조력, 상대론적 효과 [19][20]등이 있습니다.태양으로부터의 방사선 압력의 영향은 달 [18]거리에 ±3.6mm의 양을 기여한다.

순간적인 불확실성은 몇 밀리미터이지만, 측정된 달 거리는 보통 달에 걸쳐 평균값에서 21,000km(13,000mi) 이상 변할 수 있다.이러한 동요는 잘 이해되고[21] 있으며 수천 년 [19]동안 달 거리를 정확하게 모델링할 수 있습니다.

달과 지구의 거리는 2014년에 단계적으로 변화한다.
월상: 0 (1) – 초승달, 0.25 – 1분기, 0.5 – 보름달, 0.75 – 지난 분기
달과 지구의 중심 사이의 700일 동안의 거리 변화.

조수 방산

조석력의 작용을 통해 지구 자전의 각운동량이 서서히 달의 [22]궤도로 옮겨지고 있다.그 결과 지구의 자전 속도는 점차 감소하고 있으며(세기당 [23][24][25][26]2.4밀리초의 속도로), 달 궤도는 점차 확대되고 있습니다.현재의 경기후퇴율은 연간 3.830±0.008cm이다.[21][24]하지만, 이 비율은 최근에 증가했다고 믿어지는데, 이는 달의 나이가 약 40억 [27]년으로 추정되는 반면, 1년에 3.8 cm의 비율은 달이 15억 년밖에 되지 않았다는 것을 의미하기 때문이다.또한 이 비정상적으로 높은 경기 후퇴율이 계속 [28]가속화될 것으로 생각된다.

명왕성과 카론처럼 지구와 달이 조석으로 고정될 때까지 달 거리가 계속 늘어날 것으로 예상된다.이것은 달의 공전 주기의 지속 시간이 지구의 자전 주기와 같을 때 발생할 것이며, 이것은 현재 우리 날의 47개로 추정된다.그러면 두 물체는 평형을 이루게 되고 더 이상의 회전 에너지는 교환되지 않을 것이다.그러나 모형들은 태양계의 예상 수명보다 훨씬 긴 500억 년이 걸릴 [29]것으로 예측하고 있다.

궤도 역사

레이저 측정은 평균 달 거리가 증가하고 있다는 것을 보여주는데, 이는 과거 달이 더 가까웠다는 것과 지구의 낮이 더 짧았다는 것을 의미한다.캄파니아 시대의 연체동물 껍데기에 대한 화석 연구는 그 기간 동안 연간 372일(23시간 33분)이 있었다는 것을 보여주는데, 이는 달 거리가 약 60.05일(383,000km 또는 238,000mi)[22]임을 의미한다.달의 평균 거리가 약 52였다는 지질학적 증거가 있다.REarth (332,000km 또는 205,000mi) 선캄브리아 시대, 25억 년 BP.[27]

널리 받아들여지는 이론인 거대 충돌 가설은 달이 지구와 다른 행성 사이의 재앙적인 충돌의 결과로 만들어졌고, 그 결과 초기 거리 3.8에서 파편이 다시 축적되었다고 말한다.REarth (24,000km 또는 15,000mi).[30]이 이론에서, 초기 충격은 45억 [31]년 전에 일어났다고 가정합니다.

측정 이력

1950년대 후반까지 모든 달 거리 측정은 광학 각도 측정에 근거했습니다. 가장 먼저 정확한 측정은 기원전 2세기에 히파르코스에 의해 이루어졌습니다.우주시대는 이 값의 정밀도가 크게 향상되는 전환점이 되었다.1950년대와 1960년대 동안, 컴퓨터 [32]처리와 모델링의 이점을 가지고 행해진 레이더, 레이저, 그리고 우주선을 이용한 실험이 있었다.

이 섹션은 달 거리를 결정하는 역사적으로 중요하거나 다른 흥미로운 방법을 설명하기 위한 것이며, 포괄적인 목록이나 포괄적인 목록을 의도하지는 않는다.

시차

달 거리를 결정하는 가장 오래된 방법은 여러 위치에서 달과 선택된 기준점 사이의 각도를 동시에 측정하는 것이었다.동기화는 사전 결정된 시간에 측정하거나 모든 당사자가 관찰할 수 있는 이벤트 중에 조정될 수 있습니다.정확한 기계 크로노미터 이전에 동기 이벤트는 일반적으로 월식, 즉 달이 자오선을 가로지르는 순간이었다(관측자가 같은 경도를 공유하는 경우).이 측정 기술은 달 시차라고 알려져 있습니다.

정확도를 높이려면 대기를 통과하는 빛의 굴절 및 왜곡을 고려하도록 측정된 각도를 조정하는 등 특정 조정을 수행해야 합니다.

월식

달까지의 거리를 측정하려는 초기의 시도는 지구의 반지름에 대한 지식과 태양이 달보다 훨씬 더 멀리 있다는 이해와 결합된 월식의 관측을 이용했다.월식의 형상을 관측하는 것으로, 삼각법을 이용해 달 거리를 산출할 수 있다.

이 기술을 사용하여 달 거리를 측정하는 시도에 대한 최초의 설명은 기원전[33] 4세기 그리스의 천문학자이자 수학자인 아리스타르코스에 의해 그리고 나중에 히파르코스에 의해 59-67의 결과가 나왔다.REarth (376000~427000km 또는 233000~265000mi).[34]이 방법은 나중에 프톨레마이오스의 작품에서 발견되었는데,[35] 프톨레마이오스는 그 결과물을 만들었다.64+1/6 REarth ([36]409000km 또는 253000mi).

자오선 교차로

프랑스 천문학자 A.C.D.의 탐험. 크롬멜린은 같은 날 밤 두 곳에서 달의 자오선이 지나가는 것을 관찰했다.1905년부터 1910년까지의 세심한 측정은 그리니치와 [37]희망봉에서 특정 달 분화구(뫼스팅 A)가 지역 자오선을 가로지르는 순간의 표고 각도를 측정했다.거리는 30km의 불확실성으로 계산되었고, 이것은 다음 반세기 동안 달 거리 값으로 남아있었다.

엄폐

달이 배경별을 가리는 순간(또는 이와 유사하게, 달과 배경별 사이의 각도를 미리 정해진 순간에 측정함)을 기록함으로써, 달 거리는 알려진 여러 곳에서 측정되는 한 결정될 수 있다.

천문학자 오키프와 앤더슨은 1952년 [38]9개 지점에서 4개의 엄폐물을 관측함으로써 달 거리를 계산했다.그들은 384407.6±4.7km(238,859.8±2.9mi)의 반장축을 계산했다.이 값은 Irene Fischer에 의해 1962년에 개량되었으며, Irene Fischer는 업데이트된 측지 데이터를 통합하여 384403.7±2km(238,857.4±1mi)[7]의 값을 산출했다.

레이더

1957년 미국 해군 연구소에서 레이더 신호의 반향을 이용해 지구와 달의 거리를 측정하는 실험이 실시되었다.2μs에 이르는 레이더 펄스는 50피트(15m) 직경의 라디오 접시에서 방송되었다.전파가 달 표면에서 메아리친 후, 귀환 신호가 감지되고 지연 시간이 측정되었다.그 측정으로 거리를 계산할 수 있었다.그러나 실제로는 신호 대 잡음비가 너무 낮았기 때문에 정확한 측정을 [39]신뢰할 수 없었습니다.

이 실험은 1958년 영국의 왕립 레이더 연구소에서 반복되었다.5μs 지속 레이더 펄스는 초당 260펄스의 반복 속도로 2메가와트의 피크 전력으로 전송되었다.전파가 달 표면에서 메아리친 후, 귀환 신호가 감지되고 지연 시간이 측정되었다.오실로스코프 트레이스를 사진 필름에 겹쳐 신뢰성 높은 신호를 얻기 위해 여러 신호를 함께 추가했습니다.측정에서 거리는 1.25km(0.777mi)[40]의 불확실성으로 계산되었다.

이러한 초기 실험은 개념 증명 실험으로 의도되었으며 하루만 지속되었습니다.한 달 동안 진행된 후속 실험에서 384402±1.2km(238,856±0.75mi)[41]의 반지름이 나왔는데, 이는 당시 달 거리를 가장 정확하게 측정한 것이었다.

레이저 측거

아폴로 11호의 달 레이저 거리 측정 실험

달 표면에서 반사된 레이저 펄스의 왕복 시간을 측정하는 실험은 1962년 미국 매사추세츠공대(MIT)와 크림 천체물리관측소([42]소련) 팀이 함께 했다.

1969년 아폴로호 임무 중 우주비행사들은 이 기술의 정확성과 정밀성을 개선하기 위해 역반사기를 달 표면에 설치했다.측정은 계속 진행 중이며 여러 레이저 설비를 포함합니다.달 레이저 거리 측정 실험의 순간 정밀도는 몇 밀리미터 분해능을 얻을 수 있으며, 지금까지 달 거리를 측정하는 가장 신뢰할 수 있는 방법입니다.반장축은 384,399.[2]0km로 결정되었다.

아마추어 천문학자 및 시민 과학자

정확한 타이밍 장치, 고해상도 디지털 카메라, GPS 수신기, 강력한 컴퓨터, 그리고 거의 즉각적인 통신의 현대적 접근성 덕분에 아마추어 천문학자들은 달 거리를 고정밀로 측정할 수 있게 되었다.

2007년 5월 23일, 레귤러스가 거의 관측되고 있는 동안 달의 디지털 사진이 그리스와 영국의 두 곳에서 촬영되었다.달과 선택된 배경별 사이의 시차를 측정함으로써, 달 거리가 [43]계산되었다.

2014년 [17]4월 15일 월식 기간 동안 "아리스타르쿠스 캠페인"이라고 불리는 보다 야심찬 프로젝트가 수행되었다.이 행사 기간 동안, 참가자들은 달이 뜨는 순간부터 최고 고도가 되는 지점(최고점)까지 5장의 디지털 사진을 녹화하도록 초대받았다.

이 방법은 달이 지평선에 있을 때보다 하늘에서 가장 높은 지점에 있을 때 관측자와 가장 가깝다는 사실을 이용했다.비록 달이 지평선 근처에 있을 때 가장 큰 것처럼 보이지만, 그 반대는 사실이다.이 현상은 달의 착각으로 알려져 있다.거리의 차이가 나는 이유는 달의 중심에서 지구의 중심까지의 거리는 거의 밤 내내 일정하지만, 지구 표면의 관측자는 실제로 지구 중심에서 지구 반경 1에 있기 때문이다.이 간격띄우기는 달이 머리 위에 있을 때 달과 가장 가깝게 접근합니다.

현대 카메라는 이제 달을 감지하기에 충분한 정밀도로 포착할 수 있는 해상도 수준에 도달했고, 더 중요한 것은 겉으로 보이는 이 작은 크기의 변화를 측정할 수 있다.이 실험의 결과는 LD = 60.51+3.91-4
.19로 계산되었다. R그날 밤 허용치는 60.61이었다Earth.R이는 3%의 정확도를 의미합니다Earth.이 방법의 장점은 측정 장비만 필요한 현대식 디지털 카메라(정확한 시계와 GPS 수신기가 장착됨)라는 것입니다.

아마추어 천문학자들이 수행할 수 있는 달 거리 측정의 다른 실험 방법에는 다음이 포함됩니다.

  • 달이 페넘브라에 들어가기 전과 완전히 일식된 후의 사진을 찍는 것.
  • 가능한 한 정확하게 일식 시간을 측정합니다.
  • 지구 그림자의 모양과 크기가 선명하게 보이는 부분일식 사진을 잘 찍습니다.
  • 같은 시야에서 스피카와 화성을 포함한 달의 사진을 다양한 장소에서 촬영.

「 」를 참조해 주세요.

레퍼런스

  1. ^ a b c d e Battat, J. B. R.; Murphy, T. W.; Adelberger, E. G. (January 2009). "The Apache Point Observatory Lunar Laser-ranging Operation (APOLLO): Two Years of Millimeter-Precision Measurements of the Earth-Moon Range". Astronomical Society of the Pacific. 121 (875): 29–40. Bibcode:2009PASP..121...29B. doi:10.1086/596748. JSTOR 10.1086/596748.
  2. ^ a b Williams, James G.; Dickey, Jean O. (2002). "Lunar geophysics, geodesy and dynamics". 13th International Workshop on Laser Ranging. Goddard Space Flight Center.{{cite web}}: CS1 maint :url-status (링크)
  3. ^ a b Murphy, T W (1 July 2013). "Lunar laser ranging: the millimeter challenge" (PDF). Reports on Progress in Physics. 76 (7): 2. arXiv:1309.6294. Bibcode:2013RPPh...76g6901M. doi:10.1088/0034-4885/76/7/076901. PMID 23764926. S2CID 15744316.
  4. ^ "NEO Earth Close Approaches". Neo.jpl.nasa.gov. Archived from the original on 2014-03-07. Retrieved 2016-02-22.
  5. ^ Williams, J. G.; Newhall, X. X.; Dickey, J. O. (15 June 1996). "Relativity parameters determined from lunar laser ranging" (PDF). Physical Review D. 53 (12): 6730–6739. Bibcode:1996PhRvD..53.6730W. doi:10.1103/PhysRevD.53.6730. PMID 10019959.
  6. ^ Shuch, H. Paul (July 1991). "Measuring the mass of the earth: the ultimate moonbounce experiment" (PDF). Proceedings, 25th Conference of the Central States VHF Society: 25–30. Retrieved 28 February 2016.
  7. ^ a b Fischer, Irene (August 1962). "Parallax of the moon in terms of a world geodetic system" (PDF). The Astronomical Journal. 67: 373. Bibcode:1962AJ.....67..373F. doi:10.1086/108742.
  8. ^ Dickey, J. O.; Bender, P. L.; et al. (22 July 1994). "Lunar Laser Ranging: A Continuing Legacy of the Apollo Program" (PDF). Science. 265 (5171): 482–490. Bibcode:1994Sci...265..482D. doi:10.1126/science.265.5171.482. PMID 17781305. S2CID 10157934.
  9. ^ "Is the Moon moving away from the Earth? When was this discovered? (Intermediate) - Curious About Astronomy? Ask an Astronomer". Curious.astro.cornell.edu. Retrieved 2016-02-22.
  10. ^ C.D. Murray & S.F. Dermott (1999). Solar System Dynamics. Cambridge University Press. p. 184.
  11. ^ Dickinson, Terence (1993). From the Big Bang to Planet X. Camden East, Ontario: Camden House. pp. 79–81. ISBN 978-0-921820-71-0.
  12. ^ Lasater, A. Brian (2007). The dream of the West : the ancient heritage and the European achievement in map-making, navigation and science, 1487–1727. Morrisville: Lulu Enterprises. p. 185. ISBN 978-1-4303-1382-3.
  13. ^ Leslie, William T. Fox ; illustrated by Clare Walker (1983). At the sea's edge : an introduction to coastal oceanography for the amateur naturalist. Englewood Cliffs, N.J.: Prentice-Hall. p. 101. ISBN 978-0130497833.
  14. ^ Williams, Dr. David R. (18 November 2015). "Planetary Fact Sheet - Ratio to Earth Values". NASA Goddard Space Flight Center. Retrieved 28 February 2016.
  15. ^ a b Groten, Erwin (1 April 2004). "Fundamental Parameters and Current (2004) Best Estimates of the Parameters of Common Relevance to Astronomy, Geodesy, and Geodynamics by Erwin Groten, IPGD, Darmstadt" (PDF). Journal of Geodesy. 77 (10–11): 724–797. Bibcode:2004JGeod..77..724.. doi:10.1007/s00190-003-0373-y. S2CID 16907886. Retrieved 2 March 2016.
  16. ^ "International Astronomical Union IAU". www.iau.org. Retrieved 5 May 2019.
  17. ^ a b Zuluaga, Jorge I.; Figueroa, Juan C.; Ferrin, Ignacio (19 May 2014). "The simplest method to measure the geocentric lunar distance: a case of citizen science": (page needed). arXiv:1405.4580. Bibcode:2014arXiv1405.4580Z. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
  18. ^ a b Reasenberg, R.D.; Chandler, J.F.; et al. (2016). "Modeling and Analysis of the APOLLO Lunar Laser Ranging Data". arXiv:1608.04758 [astro-ph.IM].
  19. ^ a b Vitagliano, Aldo (1997). "Numerical integration for the real time production of fundamental ephemerides over a wide time span" (PDF). Celestial Mechanics and Dynamical Astronomy. 66 (3): 293–308. Bibcode:1996CeMDA..66..293V. doi:10.1007/BF00049383. S2CID 119510653.
  20. ^ Park, Ryan S.; Folkner, William M.; Williams, James G.; Boggs, Dale H. (2021). "The JPL Planetary and Lunar Ephemerides DE440 and DE441". The Astronomical Journal. 161 (3): 105. doi:10.3847/1538-3881/abd414. ISSN 1538-3881.
  21. ^ a b Folkner, W. M.; Williams, J. G.; et al. (February 2014). "The Planetary and Lunar Ephemerides DE430 and DE431" (PDF). The Interplanetary Network Progress Report. 42–169.
  22. ^ a b Winter, Niels J.; Goderis, Steven; Van Malderen, Stijn J.M.; et al. (18 February 2020). "Subdaily-Scale Chemical Variability in a Rudist Shell: Implications for Rudist Paleobiology and the Cretaceous Day-Night Cycle". Paleoceanography and Paleoclimatology. 35 (2). doi:10.1029/2019PA003723.
  23. ^ Choi, Charles Q. (19 November 2014). "Moon Facts: Fun Information About the Earth's Moon". Space.com. TechMediaNetworks, Inc. Retrieved 3 March 2016.
  24. ^ a b Williams, James G.; Boggs, Dale H. (2016). "Secular tidal changes in lunar orbit and Earth rotation". Celestial Mechanics and Dynamical Astronomy. 126 (1): 89–129. doi:10.1007/s10569-016-9702-3. ISSN 1572-9478. S2CID 124256137.
  25. ^ Stephenson, F. R.; Morrison, L. V.; Hohenkerk, C. Y. (2016). "Measurement of the Earth's rotation: 720 BC to AD 2015". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 472 (2196): 20160404. doi:10.1098/rspa.2016.0404. PMC 5247521. PMID 28119545.
  26. ^ Morrison, L. V.; Stephenson, F. R.; Hohenkerk, C. Y.; Zawilski, M. (2021). "Addendum 2020 to 'Measurement of the Earth's rotation: 720 BC to AD 2015". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 477 (2246): 20200776. doi:10.1098/rspa.2020.0776. S2CID 231938488.
  27. ^ a b Walker, James C. G.; Zahnle, Kevin J. (17 April 1986). "Lunar nodal tide and distance to the Moon during the Precambrian" (PDF). Nature. 320 (6063): 600–602. Bibcode:1986Natur.320..600W. doi:10.1038/320600a0. hdl:2027.42/62576. PMID 11540876. S2CID 4350312.
  28. ^ Bills, B.G. & Ray, R.D. (1999), "Lunar Orbital Evolution: A Synthesis of Recent Results", Geophysical Research Letters, 26 (19): 3045–3048, Bibcode:1999GeoRL..26.3045B, doi:10.1029/1999GL008348
  29. ^ Cain, Fraser (2016-04-12). "WHEN WILL EARTH LOCK TO THE MOON?". Universe Today. Universe Today. Retrieved 1 September 2016.
  30. ^ Canup, R. M. (17 October 2012). "Forming a Moon with an Earth-like Composition via a Giant Impact". Science. 338 (6110): 1052–1055. Bibcode:2012Sci...338.1052C. doi:10.1126/science.1226073. PMC 6476314. PMID 23076098.
  31. ^ "The Theia Hypothesis: New Evidence Emerges that Earth and Moon Were Once the Same". The Daily Galaxy. 2007-07-05. Retrieved 2013-11-13.
  32. ^ Newhall, X.X; Standish, E.M; Williams, J. G. (Aug 1983). "DE 102 - A numerically integrated ephemeris of the moon and planets spanning forty-four centuries". Astronomy and Astrophysics. 125 (1): 150–167. Bibcode:1983A&A...125..150N. ISSN 0004-6361. Retrieved 28 February 2016.
  33. ^ Gutzwiller, Martin C. (1998). "Moon–Earth–Sun: The oldest three-body problem". Reviews of Modern Physics. 70 (2): 589–639. Bibcode:1998RvMP...70..589G. doi:10.1103/RevModPhys.70.589.
  34. ^ Sheehan, William; Westfall, John (2004). The transits of Venus. Amherst, N.Y.: Prometheus Books. pp. 27–28. ISBN 978-1-59102-175-9.
  35. ^ 특히 페이지 33을 참조하십시오: "히파르코스에 대해 우리가 아는 거의 모든 것은 프톨레마이오스를 통해 우리에게 전해집니다Webb, Stephen (1999), "3.2 Aristarchus, Hipparchus, and Ptolemy", Measuring the Universe: The Cosmological Distance Ladder, Springer, pp. 27–35, ISBN 978-1-85233-106-1."
  36. ^ Helden, Albert van (1986). Measuring the universe : cosmic dimensions from Aristarchus to Halley (Repr. ed.). Chicago: University of Chicago Press. p. 16. ISBN 978-0-226-84882-2.
  37. ^ Fischer, Irène (7 November 2008). "The distance of the moon". Bulletin Géodésique. 71 (1): 37–63. Bibcode:1964BGeod..38...37F. doi:10.1007/BF02526081. S2CID 117060032.
  38. ^ O'Keefe, J. A.; Anderson, J. P. (1952). "The earth's equatorial radius and the distance of the moon" (PDF). Astronomical Journal. 57: 108–121. Bibcode:1952AJ.....57..108O. doi:10.1086/106720.
  39. ^ Yaplee, B. S.; Roman, N. G.; Scanlan, T. F.; Craig, K. J. (30 July – 6 August 1958). "A lunar radar study at 10-cm wavelength". Paris Symposium on Radio Astronomy. IAU Symposium no. 9 (9): 19. Bibcode:1959IAUS....9...19Y.
  40. ^ Hey, J. S.; Hughes, V. A. (30 July – 6 August 1958). "Radar observation of the moon at 10-cm wavelength". Paris Symposium on Radio Astronomy. 9 (9): 13–18. Bibcode:1959IAUS....9...13H. doi:10.1017/s007418090005049x.
  41. ^ Yaplee, B. S.; Knowles, S. H.; et al. (January 1965). "The mean distance to the Moon as determined by radar". Symposium - International Astronomical Union. 21: 2. Bibcode:1965IAUS...21...81Y. doi:10.1017/S0074180900104826.
  42. ^ Bender, P. L.; Currie, D. G.; Dicke, R. H.; et al. (October 19, 1973). "The Lunar Laser Ranging Experiment" (PDF). Science. 182 (4109): 229–238. Bibcode:1973Sci...182..229B. doi:10.1126/science.182.4109.229. PMID 17749298. S2CID 32027563. Retrieved April 27, 2013.
  43. ^ Wright, Ernie. "Overhead view of the Earth-Moon system, to scale Lunar Parallax: Estimating the Moon's Distance". Retrieved 29 February 2016.

외부 링크