사각형 디스테노이드 벌집
Tetragonal disphenoid honeycomb| 사각형 디셰노이드 사면체 벌집 | |
|---|---|
 | |
| 유형 | 볼록 균일한 벌집 쌍대 |
| 콕서터-딘킨 도표 | |
| 셀 타입 |  사각형 디스포이드 |
| 얼굴형 | 이등변 삼각형 {3} |
| 꼭지점 도형 |  사각형 육면체 |
| 스페이스 그룹 | Im3m (229) |
| 대칭 | [[4, 3, 4]] |
| 콕서터군 | ~ 3 스타일 [4, 3, 4] |
| 듀얼 | 비트런치 큐빅 벌집 |
| 특성. | 세포 전이, 안면 전이, 정점 전이 |
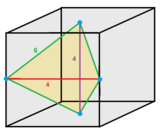
사각형 디스포이드 사면체 벌집은 동일한 사각형 디스포이드 셀로 구성된 유클리드 3공간의 공간을 채우는 테셀레이션(또는 벌집)이다.셀은 4개의 동일한 이등변 삼각형 면으로 면 전이됩니다.존 호튼 콘웨이는 그것을 사방정계라고 부르거나 사방정계라고 [1]줄인다.
셀은 정점이 두 면과 두 모서리를 중심으로 하는 변환 큐브의 1/12로 볼 수 있습니다.가장자리 중 4개는 6셀에 속하고, 2개는 4셀에 속합니다.
사면체 디셰노이드 벌집은 균일한 비트런치 큐빅 벌집 중 쌍대이다.
정점은 A/D*
3 격자를*
3 형성하며, 이는 체심 입방 격자라고도 합니다.
기하학.
이 벌집 모양의 꼭지점 도형은 테트라키스 입방체입니다. 각 꼭지점에서 24개의 디셰노이드가 만나죠.이 24개의 디셰노이드의 결합은 마름모꼴 12면체를 형성한다.테셀레이션의 각 가장자리는 각각 인접한 이등변 삼각면의 밑면 또는 변의 한쪽을 형성하는지 여부에 따라 4개 또는 6개의 디셰이드에 의해 둘러싸여 있다.모서리가 인접한 이등변 삼각형의 밑면을 형성하고 4개의 이등변으로 둘러싸이면 불규칙한 8면체를 형성합니다.가장자리가 인접한 이등변 삼각형 면의 동일한 두 변 중 하나를 형성할 때, 모서리를 둘러싼 6개의 이등변체는 삼각삼각형이라고 불리는 특별한 형태의 평행입방체를 형성합니다.
정방정방정형 벌집의 배향은 입방정형 벌집을 시작으로 x x x 및 y즉, 각 입방정체를 대각선 경로 사면으로 분할할 때까지 분할)로 분할하여 얻을 수 있다.(0, 0, 0)과 (1, 1, 1) 사이의 거리가 (0, 0, 0)과 (0, 0, 1) 사이의 거리와 같아집니다.
헥사키스 큐빅 벌집
| 헥사키스 큐빅 벌집 피라미디유[2] | |
|---|---|
 | |
| 유형 | 듀얼 균일한 벌집 |
| 콕서터-딘킨 도표 | |
| 감방 | 이등각뿔 |
| 얼굴 | 삼각형 광장 |
| 스페이스 그룹 파이버폴드 표기법 | PM3m (221) 4−:2 |
| 콕서터군 | ~ 3 스타일 [4, 3, 4] |
| 꼭지점 도형 | |
| 듀얼 | 잘린 입방체 벌집 |
| 특성. | 세포 전이 |
육각형 벌집은 유클리드 3-공간에서 균일한 공간 채우기 테셀레이션(또는 벌집)이다.존 호튼 콘웨이는 그것을 피라미디유라고 [2]부른다.
셀은 한 면에 4개의 정점을 사용하여 큐브 중심에 있는 변환 큐브에서 볼 수 있습니다.가장자리는 각각의 주위에 있는 셀 수에 따라 색칠됩니다.
이것은 각 입방체가 중앙점에 의해 6개의 정사각형 피라미드 셀로 세분된 입방체 벌집처럼 보일 수 있습니다.
면에는 정사각형 타일링과 삼각형의 절반이 제거된 평평한 삼각형 타일링의 두 가지 유형이 있습니다.
| 타일링 비행기 |  |  |
|---|---|---|
| 대칭 | p4m, [4,4] (*442) | ppmm, [12,2,128](*222) |
관련 벌집
이는 팔면체와 잘린 입방체 셀이 있는 잘린 입방체 벌집과 이중적입니다.
피라미드실의 정사각형 피라미드가 베이스에 결합되면, 정사각형 2각형 벌집 또는 정류된 입방체 벌집의 쌍대라고 불리는 동일한 정점과 모서리를 가진 또 다른 벌집이 만들어집니다.
이는 2차원 테트라키스 정사각형 타일링과 유사합니다.
네모난 이원뿔 벌집
| 네모난 이원뿔 벌집 타원형 옥타헤드리유[2] | |
|---|---|
 | |
| 유형 | 듀얼 균일한 벌집 |
| 콕서터-딘킨 도표 | |
| 감방 | 사각형 이면체 |
| 얼굴 | 삼각형 |
| 스페이스 그룹 파이버폴드 표기법 | PM3m (221) 4−:2 |
| 콕서터군 | ~ 3 스타일 [4, 3, 4] |
| 꼭지점 도형 | |
| 듀얼 | 정류된 큐빅 벌집 |
| 특성. | 셀 전이성, 페이스 전이성 |
정사각형 2각형 벌집은 유클리드 3-공간에서 균일한 공간 채우기 테셀레이션(또는 벌집)이다.존 호튼 콘웨이는 그것을 타원형 옥타헤드리유 [1]또는 오복타헤드리유라고 부른다.
셀은 중앙 모서리에 4개의 정점이 있고 반대 면에 2개의 정점이 있는 변환 큐브 내에 배치되어 있습니다.가장자리는 가장자리 주변의 셀 수로 색칠되고 레이블이 지정됩니다.
이것은 각 입방체가 중앙점에 의해 6개의 정사각형 피라미드 셀로 세분된 입방체 벌집처럼 보일 수 있습니다.원래의 입방체 벌집 벽이 제거되어 정사각형 피라미드 쌍이 정사각형 쌍체(옥타헤드라)로 결합됩니다.정점과 모서리 골격은 육각형 벌집과 동일합니다.
면이 있는 평면에는 한 가지 유형이 있습니다: 삼각형의 절반이 구멍으로 되어 있는 평평한 삼각형 타일링입니다.이것들은 원래의 큐브를 얼굴 모양으로 잘라냅니다.또한 팔면체 셀의 중심을 통과하는 비면 구멍으로 존재하는 정사각형 타일링 평면도 있습니다.
| 타일링 비행기 |  정사각형 타일 "구멍" |  편평한 삼각형 타일링 |
|---|---|---|
| 대칭 | p4m, [4,4] (*442) | ppmm, [12,2,128](*222) |
관련 벌집
이는 팔면체 및 육면체 셀이 있는 정류된 입방체 벌집과 이중적입니다.
박엽성 디스포이덜 벌집
| 박엽성 디스포이덜 벌집 여덟 번째 피라미디유[3] | |
|---|---|
| (이미지 없음) | |
| 유형 | 듀얼 균일한 벌집 |
| 콕서터-딘킨 도표 | |
| 감방 | 필릭 디스테노이드 |
| 얼굴 | 마름모꼴 삼각형 |
| 스페이스 그룹 파이버폴드 표기법 콕서터 표기법 | Im3m (229) 8o:2 [[4,3,4]] |
| 콕서터군 | [4, 3, 4], ~ 3({스타일 }) |
| 꼭지점 도형 | |
| 듀얼 | 잡동사니 큐빅 벌집 |
| 특성. | 세포 전이성, 안면 전이성 |
엽상분사 벌집은 유클리드 3공간에서 균일한 공간을 채우는 테셀레이션(또는 벌집)이다.존 호튼 콘웨이는 이걸 8번째 [3]피라미드라고 불러요
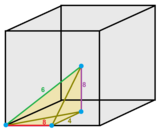
셀은 정점이 배치된 변환 큐브의 1/48로 볼 수 있습니다. 즉, 한 모서리, 한 모서리 중심, 한 면 중심 및 큐브 중심입니다.가장자리 색상과 레이블은 가장자리 주위에 존재하는 셀 수를 지정합니다.6개의 엽상세포가 공통의 대각선축을 공유하고 있는 작은 입방체의 1/6입니다.
관련 벌집
「 」를 참조해 주세요.
레퍼런스
- Gibb, William (1990), "Paper patterns: solid shapes from metric paper", Mathematics in School, 19 (3): 2–4, 에 재인쇄되었습니다.
- 를 클릭합니다Senechal, Marjorie (1981), "Which tetrahedra fill space?", Mathematics Magazine, Mathematical Association of America, 54 (5): 227–243, doi:10.2307/2689983, JSTOR 2689983.
- Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). "21. Naming Archimedean and Catalan Polyhedra and Tilings". The Symmetries of Things. A K Peters, Ltd. pp. 292–298. ISBN 978-1-56881-220-5.