소산

기초 산술은 덧셈, 뺄셈, 곱셈, 나눗셈과 같은 기본적인 숫자 연산을 포함하는 수학의 한 분야입니다. 추상화 수준이 낮고 적용 범위가 넓으며 모든 수학의 기초가 되는 위치로 인해 초등 산술은 일반적으로 학교에서 가르치는 수학의 첫 번째 분야로 알려져 있습니다.^[1]^[2]

자리수

숫자는 숫자 체계에서 숫자의 값을 나타내는 데 사용됩니다. 가장 많이 사용되는 숫자는^[3] 0에서 9까지의 아라비아 숫자입니다. 힌두 아라비아 숫자 체계는 가장 일반적으로 사용되는 숫자 체계로, 이 숫자들을 사용하여 숫자를 나타내는 데 사용되는 위치 표기 체계입니다.^[4] 그러나 알래스카, 캐나다, 그린란드의 에스키모-알류트 언어의 베이스 20과 같은 다른 시스템이 사용됩니다. 이것은 다른 숫자들을 필요로 합니다 - 이 언어들은 일반적으로 Kaktovik 숫자를 사용합니다. 텔레폴 언어는 베이스-27을 사용하는 것으로 알려져 있고, 컴퓨터는 바이너리(베이스-2)를 사용하는 것으로 알려져 있습니다.^{[citation needed]} 그 외에는 로마 숫자와 같은 비위치 숫자 체계가 사용되기도 합니다.^[5] 비위치 시스템의 단점은 일반적으로 표현 가능한 수가 가장 많다는 것입니다.

후계자 기능 및 순서

초등 산술에서 자연수(0 포함)의 계승은 그 수에 1의 값을 더한 결과입니다. 자연수(0은 제외)의 선행은 그 수에서 1의 값을 뺀 결과입니다. 예를 들어, 0의 계승자는 1이고 11의 이전 계승자는 10입니다( $0+1=1$ + $0+1=1$ = $0+1=1$ ${\displaystyle$ 0 + 1 = $1}$ 및 $11-1=10$ - $11-1=10$ = $11-1=10$ ${\displaystyle 11-1$ = $10}).$ 모든 자연수에는 계승자가 있고, 첫 번째 자연수(0 또는 1)를 제외한 모든 자연수에는 계승자가 있습니다.^[6]

자연수에는 총 주문이 있습니다. 하나의 숫자가 다른 숫자보다 크면 $>$ ${\displaystyle$ $>$ 후자가 전자보다 작습니다 $<$ ${\displaystyle$ $<$ 예를 들어 3이 8보다 작으면( $3<8$ < $3<8$ ${\displaystyle$ $3$ $< 8}),$ 8이 3보다 큽니다( $8>3$ > $8>3$ ${\displaystyle 8>$ 3 $}).$ 자연수도 잘 정리되어 있습니다.

계산

카운트에는 집합의 각 개체에 자연수를 할당하는 것이 포함되며, 첫 번째 개체에 대해 하나로 시작하여 후속 개체에 대해 하나씩 증가합니다. 집합의 개체 수는 집합의 개체에 할당된 가장 높은 자연수와 동일한 카운트입니다. 이 카운트는 세트의 카디널리티라고도 합니다. 수많은 집합이 아닌 집합이라고 알려진 일부 집합은 주문할 수 없습니다. 예를 들어, 유리수를 열거(순서)할 수 있지만 실수는 셀 수 없습니다.

카운트는 집계 표시를 사용하여 집계하는 과정, 집합 내의 각 개체에 대해 표시를 그리는 과정일 수도 있습니다.

비공식적으로 두 세트의 요소를 모두 일대일 대응으로 맞출 수 있다면 두 세트는 동일한 카디널리티를 가집니다. (예를 들어 사과 4개와 바나나 4개는 각 사과가 남은 것 없이 각 바나나에 매칭될 수 있으므로 동일한 카디널리티를 갖습니다.)

추가

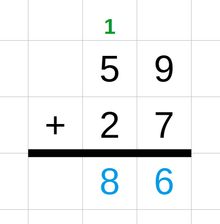
덧셈은 덧셈 또는 합이라고 불리는 두 개 이상의 숫자를 결합하여 합이라고 불리는 결합된 숫자를 산출하는 수학적 연산입니다. 숫자 2개의 덧셈은 더하기 기호 " $+$ + ${\displaystyle +}"$ 을 사용하여 표현됩니다. $+$ ^[7] 다음 규칙에 따라 수행됩니다.

두 숫자의 합은 개별 값을 더한 숫자와 같습니다.^[8]
덧셈이 추가되는 순서는 합에 영향을 미치지 않습니다. 이것은 덧셈의 교환 속성으로 알려져 있습니다. 예를 들어, (a + b)와 (b + a)는 동일한 출력을 생성합니다.^[9]^[8]
두 숫자의 합은 고유하며, 이는 주어진 숫자의 합에 대한 정답이 하나뿐이라는 것을 의미합니다.^[8]
덧셈에는 뺄셈이라는 역연산이 있는데, 둘 이상의 수 사이의 차이를 찾는 데 사용할 수 있습니다.

덧셈은 수량 비교, 수량 결합, 측정 등 다양한 맥락에서 사용됩니다.^{[citation needed]} 덧셈 알고리즘에서 "텐스" 숫자는 한 쌍의 숫자의 합이 두 자리 숫자가 될 때 "캐리 숫자"라고 합니다.^[10] 초등 산술에서 학생들은 일반적으로 정수를 더하는 법을 배우며 음수와 분수와 같은 주제에 대해 배울 수도 있습니다.

뺄셈

뺄셈은 두 숫자의 차이를 평가하는 데 사용되며, 여기서 뺄셈은 뺄셈이 되는 숫자이고, 뺄셈은 뺄셈이 되는 숫자입니다. 빼기 기호( $-$ - ${\displaystyle -})$ 를 사용하여 표시됩니다. $-$ 마이너스 부호는 음수를 표기하는 데에도 사용되며, 이들은 0에서 뺀 숫자로 간주될 수 있습니다.

뺄셈은 가환적이지 않으므로 숫자의 순서가 최종 값을 변경할 수 있습니다. $3-5$ - 5 $3-5$ 은 $3-5$ (는) $5-3$ - $5-3$ $5-3$ 과(는) 같지 않습니다 $5-3$ 기본 산술에서 미뉴엔드는 항상 서브엔드보다 커야 긍정적인 결과를 얻을 수 있습니다. 그러나 a-b와 b-a의 절대값은 같습니다(a-b = b-a).

뺄셈은 또한 분리, 결합(예: 관심 있는 집합의 부분 집합의 크기를 찾는 것) 및 다른 맥락에서 수량을 찾는 데 사용됩니다. 예를 들어, "톰은 8개의 사과를 가지고 있습니다. 사과 3개를 나눠줍니다. 몇 개나 남았나요?"는 분리를 의미하고, "톰은 8개의 사과를 가지고 있습니다. 사과 중 세 개는 녹색이고 나머지는 빨간색입니다. 빨간색은 몇 개입니까?"는 조합을 나타냅니다. 어떤 경우에는 뺄셈을 사용하여 "톰에게 사과가 좀 있었습니다."와 같이 그룹의 전체 개체 수를 찾을 수도 있습니다. 제인은 그에게 3개의 사과를 더 주어서 지금은 8개의 사과를 가지고 있습니다. 그는 몇 명으로 시작했습니까?"

뺄셈을 수행하는 몇 가지 방법이 있습니다. 전통적인 수학 방법은 손으로 계산하기에 적합한 방법을 사용하여 초등학생에게 뺄셈을 가르칩니다.^[11] 리폼 수학은 일반적으로 특정한 기술에 대한 선호가 부족하다는 것으로 구별되며, TERC의 경우 음수의 속성을 사용하는 것과 같은 2학년 학생들이 자신만의 계산 방법을 개발하도록 안내하는 것으로 대체됩니다.

현재 미국 학교에서는 차용을^{[citation needed]} 사용하여 뺄셈 방법을 가르치고 있습니다. 그러나 이전 교과서에는 차용 방법이 알려져 있었고 출판되었습니다. 목발은 윌리엄 A의 발명품입니다. 1937년 11월 연구에서 그것들을 사용한 브라우넬.^[12] 빌리는 방법은 뺄셈을 쉽게 하기 위해 십 자리에서 십 자리를 빌려 십 자리에 덧셈할 십 자리에서 십 자리를 빌려 $86-39$ - $86-39$ $86-39$ 와 같은 뺄셈 문제를 해결할 $86-39$ 수 있습니다. 예를 들어, 6에서 9를 빼면 10자리에서 10을 빌려 문제를 $70+16-39$ + $70+16-39$ - $70+16-39$ ${\displaystyle 70$ + $16-39}$ 로 만듭니다 $70+16-39$ 이것은 8을 건너서 그 위에 7을 쓰고 6 위에 1을 적음으로써 표시됩니다. 이러한 표시를 "목발"이라고 합니다.

덧셈 방법이라고도 알려진 오스트리아 방법은 특정 유럽 국가에서 가르치고 있으며 이전 세대의 일부 미국인들이 사용하고 있습니다. 목발을 사용하는 것과 달리 이 방법에서는 차입이 없습니다. 나라에 따라 다른 목발도 있습니다.^[13]^[14] 덧셈 방법은 차입 방법에서와 같이 미뉴엔드를 줄이는 것이 아니라 하위 범위를 늘리는 것을 포함합니다. 그러면 문제가 $(80+16)-(39+10)$ + $(80+16)-(39+10)$ - $(80+16)-(39+10)$ + $(80+16)-(39+10)$ ${\displaystyle (80$ + $16)$ - ( $39$ + $10)}$ {\displaystyle (80 + 16) - (39 + 10)}(으)로 변환됩니다 $(80+16)-(39+10)$ 하위 끝 자리 아래에 작은 1이 알림으로 표시됩니다.

예

숫자 792와 308을 빼면 1열부터 2는 8보다 작으며, 90에서 10을 빌리면 90이 80이 됩니다. 이 10 대 2를 더하면 문제가 $12-8$ - 8 ${\displaystyle 12-8$ 4)로 변경됩니다.

	수백	텐스	하나
		8	¹2
	7	9	2
−	3	0	8
			4

열 열에서 80과 0의 차이는 80입니다.

	수백	텐스	하나
		8	¹2
	7	9	2
−	3	0	8
		8	4

수백 열에서 700과 300의 차이는 400입니다.

	수백	텐스	하나
		8	¹2
	7	9	2
−	3	0	8
	4	8	4

결과:

$792-308=484$

곱셈

곱셈은 반복되는 덧셈의 수학적 연산입니다. 두 개의 숫자를 곱하면 그 결과 값은 곱이 됩니다. 곱해지는 수를 곱셈과 곱셈이라고 하며 모두 요인으로 알려져 있습니다. 예를 들어, 5개의 봉지가 있는데, 각각 3개의 사과가 들어 있고, 5개의 봉지 모두의 사과가 빈 봉지에 담겨 있다면, 빈 봉지에는 15개의 사과가 들어 있을 것입니다. 이는 "5 곱하기 3은 15", "5 곱하기 3은 15" 또는 "15는 5와 3의 곱"으로 표현할 수 있습니다.

곱셈은 곱셈 기호(x), 별표(*), 괄호() 또는 점(⋅)을 사용하여 표시됩니다. 따라서 "5 곱하기 3은 15"는 " $5\times 3=15$ × $5\times 3=15$ = $5\times 3=15$ ${\displaystyle$ 5 $\times$ 3= $15}",$ " $5\ast 3=15$ ∗ $5\ast 3=15$ = $15 {\displaystyle$ 5\ast $3$ =15 $(5)(3)=15$ $(5)(3)=15$ ( $(5)(3)=15$ ) = $15 {\displaystyle$ (5)(3)=15}" $5\cdot 3=15$ $5\cdot 3=15$ ⋅ $3$ = $15$ {\ $displaystyle$ 5 $\cdot$ 3=15}"와 같이 쓸 수 있습니다. 곱셈 기호는 단연코 곱셈에 가장 많이 사용되는 기호이며, 별표 표기법은 컴퓨터 프로그래밍 언어에서 가장 많이 사용됩니다. 대수학에서 곱셈 기호는 생략될 수 있습니다. 예를 들어 $xy$ $xy$ 는 $x\times y$ × y ${\displaystyle x\times$ y $}$ 를 나타냅니다 $xy$ $x\times y$

두 수가 곱해지는 순서는 결과에 영향을 미치지 않습니다. 이것은 곱셈의 교환 속성으로 알려져 있습니다. 괄호 안에 3개 이상의 숫자를 그룹화해도 결과에 영향을 미치지 않습니다. 이것은 곱셈의 연관성으로 알려져 있습니다.

곱셈 알고리즘에서 한 쌍의 자릿수의 곱의 "텐스" 자릿수를 "캐리 자릿수"라고 합니다. 표를 사용하여 한 쌍의 숫자를 곱하려면 첫 번째 숫자 행과 두 번째 숫자 열의 교차점을 찾아야 하며, 두 숫자의 곱이 포함됩니다. 대부분의 숫자 쌍은 곱하면 두 자리 숫자가 됩니다.

한 자릿수 요인에 대한 곱셈 예제

729와 3을 곱하면 1열에서 시작하여 9와 3의 곱은 27입니다. 7은 1열 아래에 쓰여지고 2는 10열 위에 캐리 숫자로 쓰여집니다.

	수백	텐스	하나
		2
	7	2	9
×			3
			7

2와 3의 곱은 6이고, 휴대 숫자는 6에 2를 더하므로 10칸 아래에 8을 적습니다.

	수백	텐스	하나
	7	2	9
×			3
		8	7

7과 3의 곱은 21이고, 이것이 마지막 자리이기 때문에 2는 캐리 자리가 아니라 1 옆에 쓰여질 것입니다.

	수백	텐스	하나
	7	2	9
×			3
2	1	8	7

결과:

3\times 729=2187

여러 자리 요인에 대한 곱셈 예제

789와 345를 곱하면 789와 5의 곱은 3945입니다.

	7	8	9
×	3	4	5
3	9	4	5

4는 10자리 숫자입니다. 승수는 4가 아니라 40입니다. 789와 40의 제품은 31560입니다.

		7	8	9
	×	3	4	5
	3	9	4	5
3	1	5	6	0

3은 수백 자리입니다. 승수는 300입니다. 789와 300의 제품은 236700입니다.

			7	8	9
		×	3	4	5
		3	9	4	5
	3	1	5	6	0
2	3	6	7	0	0

모든 제품을 추가하면,

				7	8	9
×				3	4	5
			3	9	4	5
		3	1	5	6	0
+	2	3	6	7	0	0
	2	7	2	2	0	5

결과:

$789\times 345=272205$

나누기

나눗셈은 곱셈의 역수인 산술 연산입니다.

구체적으로, 숫자 a와 0이 아닌 숫자 b가 주어졌을 때, 다른 숫자 c 곱하기 b가 a, 즉 $c\times b=a$ × $c\times b=a$ = ${\displaystyle$ c $\times$ b= $a}$ 인 경우 $c\times b=a$ b로 나눈 a는 c와 같습니다.

${\frac {a}{b}}=c$ , ${\frac {a}{b}}=c$ = ${\frac {a}{b}}=c$ ${\displaystyle {\frac {a}{b$ }= $c}$ 입니다 ${\frac {a}{b}}=c$ 예를 들어 ${\frac {6}{3}}=2$ = 2 ${\displaystyle {\frac {6}{3$ }= $2}$ 입니다 ${\frac {6}{3}}=2$

숫자 a는 배당, b는 약수, c는 몫이라고 합니다. 0으로 나누는 것은 기본 연산 수준에서는 불가능한 것으로 간주되며 일반적으로 무시됩니다.

나눗셈은 그들 사이에 빈쿨럼이라고도 불리는 수평선이 있는 약수 위에 배당금을 놓음으로써 보여질 수 있습니다. 예를 들어, b로 나눈 a는 다음과 같이 기록됩니다.

{\frac {a}{b}

이것은 구두로 "a를 b로 나눈 것" 또는 "a over b"로 읽을 수 있습니다.

나눗셈을 한 줄에 모두 표현하는 또 다른 방법은 다음과 같이 배당금을 쓴 다음에 슬래시를 쓴 다음에 약수를 쓴다는 것입니다.

a/b

이것은 대부분의 컴퓨터 프로그래밍 언어에서 분할을 지정하는 일반적인 방법입니다.

필기 또는 활자 변형은 솔리더스(분수 슬래시)를 사용하지만 배당금을 높이고 약수를 낮춥니다.

⁄ b

이러한 양식을 사용하여 분수를 표시할 수 있습니다. 공통분수는 배당과 나눗셈이 모두 숫자(일반적으로 분자와 분모라고 불리지만)인 나눗셈 표현식이며, 나눗셈을 더 평가할 필요가 있다는 의미는 없습니다.

나눗셈을 보여주는 더 기본적인 방법은 다음과 같은 방식으로 오벨루스(÷)를 사용하는 것입니다.

a\div b.

영어를 사용하지 않는 일부 문화권에서는^[which?] "a를 b로 나눈다"가 a: b로 표기됩니다. 그러나 영어 용법에서 콜론은 비율("a is to b")의 개념으로 제한됩니다.

종이 위에서 두 개의 숫자는 긴 나눗셈의 방법을 사용하여 나눗셈할 수 있습니다. 긴 나눗셈의 축약형인 짧은 나눗셈은 더 작은 나눗셈에도 사용할 수 있습니다.

덜 체계적인 방법은 각 단계에서 부분 나머지에서 더 많은 배수를 빼는 청킹의 개념을 포함합니다.

분수로 나누려면 해당 분수의 역수(위 부분과 아래 부분의 위치를 반대로)를 곱하면 됩니다. 예:

\textstyle {5\div {1 \over 2}=5\times {2 \over 1}=5\times 2=10

\textstyle {{2 \over 3}\div {2 \over 5}={2 \over 3}\times {5 \over 2}={10 \over 6}={5 \over 3}}

예

272와 8을 나누면 100자리 숫자로 시작하여 2는 8로 나눌 수 없고 20에 7을 더하면 27이 됩니다. 나눗셈 8이 27을 넘지 않고 곱할 수 있는 가장 큰 수는 3이므로, 십자열 아래에 숫자 3을 적어 몫을 구성하기 시작합니다. 27에서 24(3과 8의 곱)를 빼면 3이 나머지로 나옵니다.

	2	7	2
÷			8
		3

8은 반드시 나머지 3보다 커야 합니다. 나눗셈을 계속하기 위해 한 자리로 가면 숫자는 2입니다. 30과 2를 더하면 32가 나오는데, 이는 8로 나눗셈할 수 있고, 32와 8의 몫은 4.4입니다.

	2	7	2
÷			8
		3	4

결과:

272\div 8=34

버스정류장방법

일부 학교에서 가르치는 나눗셈의 또 다른 방법은 버스 정류장 방법인데, 때로는 다음과 같이 표기하기도 합니다.

   실적(배당)배당

위와 동일한 예를 사용하여 다음 단계를 보여 줍니다.

  034 (설명) 8) 2720 (8 × 0 = 0) 27 (2 - 0 = 2) 24 (8 × 3 = 24) 32 (27 - 24 = 3) 32 (8 × 4 = 32) 0 (32 - 32 = 0)

결론:

$272\div 8=34$

교육기준

초등 산술은 일반적으로 초등학교 또는 중등학교 수준에서 가르치고 있으며 지역 교육 기준에 의해 통제됩니다. 미국과 캐나다에서는 초등 산수를 가르칠 때 사용하는 내용과 방법에 대한 논쟁이 있었습니다.^{[citation needed]}^[15]^[16] 한 가지 문제는 계산기 대 수동 계산의 사용이었고, 일부는 계산기 사용이 암산 기술을 촉진하기 위해 제한되어야 한다고 주장했습니다. 또 다른 논쟁은 전통 수학과 개혁 수학의 구별에 초점을 맞추고 있으며, 전통적인 방법은 종종 기본 계산 기술에 더 초점을 맞추고 개혁 방법은 대수학, 통계학 및 문제 해결과 같은 상위 수준의 수학 개념에 더 중점을 둡니다.

미국에서는 1989년 전국 수학교사협의회 표준이 전통적으로 초등 산술의 일부로 간주되는 특정 주제를 대수학과 통계학과 같은 대학 수준의 개념에 더 중점을 두도록 강조하거나 생략하는 초등학교 교육과정의 변화로 이어졌습니다. 이러한 변화는 논란의 여지가 있으며, 일부에서는 이후 수학 수업에서 성공에 중요한 기본 계산 능력에 대한 강조가 부족하다고 주장합니다.

참고 항목

참고문헌

^ Mitchelmore, Michael C.; White, Paul (2012). Seel, Norbert M. (ed.). Abstraction in Mathematics Learning. Boston, MA: Springer US. pp. 31–33. doi:10.1007/978-1-4419-1428-6_516. ISBN 978-1-4419-1428-6.{{cite book}}: CS1 maint : url-status (링크)
^ Björklund, Camilla; Marton, Ference; Kullberg, Angelika (2021). "What is to be learnt? Critical aspects of elementary arithmetic skills". Educational Studies in Mathematics. 107 (2): 261–284. doi:10.1007/s10649-021-10045-0. ISSN 0013-1954.
^ "numeral system mathematics Britannica". www.britannica.com. Paragraph 2, sentence 4. Archived from the original on 2023-08-10. Retrieved 2022-11-24.
^ Tillinghast-Raby, Amory. "A Number System Invented by Inuit Schoolchildren Will Make Its Silicon Valley Debut". Scientific American. Archived from the original on 19 July 2023. Retrieved 24 July 2023.
^ ITL Education Solutions Limited (2011). Introduction to Computer Science. Pearson Education India. p. 28. ISBN 978-81-317-6030-7.
^ Madden, Daniel J.; Aubrey, Jason A. (2017). An Introduction to Proof through Real Analysis. John Wiley & Sons. p. 3. ISBN 97811199314738. {{cite book}}: 확인. isbn= 값: 길이(도움말)
^ Musser, Gary L.; Peterson, Blake E.; Burger, William F. (2013). Mathematics for Elementary Teachers: A Contemporary Approach. John Wiley & Sons. p. 87. ISBN 978-1-118-48700-6.
^ ^a ^b ^c Hall, F. M. (1972). An Introduction to Abstract Algebra. Cambridge University Press. p. 171.
^ Rosen, Kenneth (2013). Discrete Maths and Its Applications Global Edition. McGraw Hill. ISBN 978-0-07-131501-2. 부록 I 참조.
^ Resnick, L. B.; Ford, W. W. (2012). Psychology of Mathematics for Instruction. Routledge. p. 110. ISBN 978-1-136-55759-0.
^ "Everyday Mathematics4 at Home". Everyday Mathematics Online. Retrieved December 26, 2022.
^ Ross, Susan. "Subtraction in the United States: An Historical Perspective" (PDF). Microsoft Word - Issue 2 -9/23/. Archived from the original (PDF) on August 11, 2017. Retrieved June 25, 2019.
^ Klapper, Paul (1916). "The Teaching of Arithmetic: A Manual for Teachers. pp. 177". Retrieved 2016-03-11.
^ Smith, David Eugene (1913). "The Teaching of Arithmetic. pp. 77". Retrieved 2016-03-11.
^ "Debate about Teaching style of Maths". edmontonjournal.com.
^ Gollom, Mark (April 10, 2016). "Educators debate whether some math basics are 'a dead issue in the year 2016'".

외부 링크

"산술의 과학에 대한 친절한 선물" – 기본적인 산술에 대해 이야기하는 15세기 아랍 문서입니다.

[mw-1] Mitchelmore, Michael C.; White, Paul (2012). Seel, Norbert M. (ed.). Abstraction in Mathematics Learning. Boston, MA: Springer US. pp. 31–33. doi:10.1007/978-1-4419-1428-6_516. ISBN 978-1-4419-1428-6.{{cite book}}: CS1 maint : url-status (링크)

[bmk-2] Björklund, Camilla; Marton, Ference; Kullberg, Angelika (2021). "What is to be learnt? Critical aspects of elementary arithmetic skills". Educational Studies in Mathematics. 107 (2): 261–284. doi:10.1007/s10649-021-10045-0. ISSN 0013-1954.

[3] "numeral system mathematics Britannica". www.britannica.com. Paragraph 2, sentence 4. Archived from the original on 2023-08-10. Retrieved 2022-11-24.

[4] Tillinghast-Raby, Amory. "A Number System Invented by Inuit Schoolchildren Will Make Its Silicon Valley Debut". Scientific American. Archived from the original on 19 July 2023. Retrieved 24 July 2023.

[5] ITL Education Solutions Limited (2011). Introduction to Computer Science. Pearson Education India. p. 28. ISBN 978-81-317-6030-7.

[ma-6] Madden, Daniel J.; Aubrey, Jason A. (2017). An Introduction to Proof through Real Analysis. John Wiley & Sons. p. 3. ISBN 97811199314738. {{cite book}}: 확인. isbn= 값: 길이(도움말)

[mpb-7] Musser, Gary L.; Peterson, Blake E.; Burger, William F. (2013). Mathematics for Elementary Teachers: A Contemporary Approach. John Wiley & Sons. p. 87. ISBN 978-1-118-48700-6.

[hall-8] Hall, F. M. (1972). An Introduction to Abstract Algebra. Cambridge University Press. p. 171.

[rosen-9] Rosen, Kenneth (2013). Discrete Maths and Its Applications Global Edition. McGraw Hill. ISBN 978-0-07-131501-2. 부록 I 참조.

[rf-10] Resnick, L. B.; Ford, W. W. (2012). Psychology of Mathematics for Instruction. Routledge. p. 110. ISBN 978-1-136-55759-0.

[11] "Everyday Mathematics4 at Home". Everyday Mathematics Online. Retrieved December 26, 2022.

[12] Ross, Susan. "Subtraction in the United States: An Historical Perspective" (PDF). Microsoft Word - Issue 2 -9/23/. Archived from the original (PDF) on August 11, 2017. Retrieved June 25, 2019.

[13] Klapper, Paul (1916). "The Teaching of Arithmetic: A Manual for Teachers. pp. 177". Retrieved 2016-03-11.

[14] Smith, David Eugene (1913). "The Teaching of Arithmetic. pp. 77". Retrieved 2016-03-11.

[15] "Debate about Teaching style of Maths". edmontonjournal.com.

[16] Gollom, Mark (April 10, 2016). "Educators debate whether some math basics are 'a dead issue in the year 2016'".

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

Search

소산

네임스페이스

더

목차

자리수