Large Edy Simulation(LES; 대규모 와동 시뮬레이션)의 맥락에서 필터링하는 것은 Navier-Stokes 방정식에 대한 작은 스케일 범위를 솔루션에서 제거하기 위한 수학적 연산입니다.난류 시뮬레이션의 주요 어려움은 길이와 시간 척도의 넓은 범위에서 발생하기 때문에 이 작업을 통해 해결해야 할 스케일 범위를 줄임으로써 난류 시뮬레이션 비용을 절감할 수 있습니다.LES 필터 동작은 저역 통과입니다.즉, 고주파수와 관련된 스케일을 필터링 합니다.
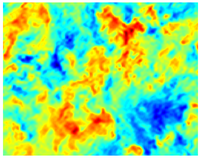
균일한 필터
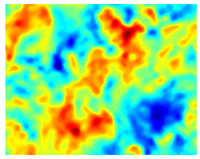
상자 필터 및 δ = /32를 사용하여 필터링된 동일한 DNS 속도 필드 
박스 필터 및 δ = /16을 사용하여 필터링된 동일한 DNS 속도 필드 물리적 공간에서의 정의
LES에서 사용되는 로우패스필터링 조작은 공간 필드 및 시간 필드에 적용할 수 있습니다: ( ) {  LES 필터 조작은 공간 또는 시간 또는 둘 다입니다.막대로 표시된 필터링된 필드는 다음과 [1][2]같이 정의됩니다.
LES 필터 조작은 공간 또는 시간 또는 둘 다입니다.막대로 표시된 필터링된 필드는 다음과 [1][2]같이 정의됩니다.

서G {\ G는 사용되는 필터 유형에 고유한 컨볼루션 커널입니다.이는 컨볼루션 연산이라고 할 수 있습니다.
사용되는 필터 유형에 고유한 컨볼루션 커널입니다.이는 컨볼루션 연산이라고 할 수 있습니다.

필터 G G는
 컷오프 길이와 시간 스케일을 사용합니다.
컷오프 길이와 시간 스케일을 사용합니다. { \} , , \ \_ { } 。Scales smaller than these are eliminated from
{ \} , , \ \_ { } 。Scales smaller than these are eliminated from  Using this definition, any field
Using this definition, any field  may be split up into a filtered and sub-filtered (denoted with a prime) portion, as
may be split up into a filtered and sub-filtered (denoted with a prime) portion, as

이것은 컨볼루션 연산이라고도 할 수 있습니다.

스펙트럼 공간의 정의
필터링 연산은 고주파와 관련된 스케일을 제거하므로 푸리에 공간에서 연산을 해석할 수 있습니다.스칼라 ( ,)、 \ ( \ symbol { } , )의

 푸리에 은 ( , \ } ( \ {} 시간
푸리에 은 ( , \ } ( \ {} 시간 주파수.{\ {\phi
주파수.{\ {\phi 의 대응하는 푸리에 변환 ) :{\ {k에 의해 필터링할 수 .
의 대응하는 푸리에 변환 ) :{\ {k에 의해 필터링할 수 .

또는,

 폭 { style \ } 에는 번호k
폭 { style \ } 에는 번호k c , { _{ c } 및 시간 필터 폭 c {\ _ { c에는
c , { _{ c } 및 시간 필터 폭 c {\ _ { c에는 컷오프 주파수 c .{ \ \도 있습니다. \phi})의
컷오프 주파수 c .{ \ \도 있습니다. \phi})의
 필터링되지 않은 부분은 다음과 같습니다
필터링되지 않은 부분은 다음과 같습니다

난류 흐름의 스펙트럼이 하위 필터 척도(최고 주파수)의 영향을 재구성하는 LES 하위 그리드 척도 모델에 중심적이기 때문에 필터링 연산의 스펙트럼 해석은 대형 와류 시뮬레이션에서 필터링 작업에 필수적이다.서브 그리드 모델링의 과제 중 하나는 낮은 주파수에서 높은 주파수로 이어지는 운동 에너지의 캐스케이드를 효과적으로 모방하는 것이다.이는 구현된 LES 필터의 스펙트럼 특성을 서브 그리드 모델링 노력에 매우 중요하게 만든다.
균질 필터 속성
균질 LES 필터는 Navier-Stokes [1]방정식에 적용할 때 다음 속성 세트를 충족해야 합니다.
- (1) 상수의 보존
- 필터링된 상수의 값은 상수와 같아야 합니다.

- 즉,

- 2. 직선성

- 3. 파생상품과의 교환

- 2개의 임의의 f displaystyle
 g\ f\ g
g\ f\ g 에
에![[f,g]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6d19d70e6a63d3650c33b1e58d1f69bbb956072) 대해 연산자communation [f에 이도입된 경우, 여기서
대해 연산자communation [f에 이도입된 경우, 여기서
![[f,g]\phi =f\circ g(\phi )-g\circ f(\phi )=f(g(\phi ))-g(f(\phi )),](https://wikimedia.org/api/rest_v1/media/math/render/svg/c16f02f51de3e6ea23348440769390f4ee0e1ea5)
- 그러면 이 세 번째 특성은 다음과 같이 표현될 수 있다.
![\left[G\star ,{\frac {\partial }{\partial s}}\right]=0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ffc45070eaa4ca1d242e99c812ab5cb6d39c772)
이러한 특성을 충족하는 필터는 일반적으로 레이놀즈 연산자가 아닙니다. 즉, 첫째,

그리고 둘째,

불균일한 필터
가장 단순한 흐름을 제외한 모든 흐름의 필터링 조작 구현은 불균일한 필터 조작입니다.즉, 흐름에 비주기적 경계가 있어 특정 유형의 필터에 문제가 발생하거나 필터 폭(\ 가 일정하지 않거나 둘 다 있음을 의미합니다.이것에 의해, 필터가 파생 기종과 함께 이동하는 것을 방지해, 정류 연산을 실시하면, 다음의 몇개의 에러 용어가 추가됩니다.
가 일정하지 않거나 둘 다 있음을 의미합니다.이것에 의해, 필터가 파생 기종과 함께 이동하는 것을 방지해, 정류 연산을 실시하면, 다음의 몇개의 에러 용어가 추가됩니다.
![{\begin{array}{rcl}\left[{\frac {\partial }{\partial {\boldsymbol {x}}}},G\star \right]\phi &=&{\frac {\partial }{\partial {\boldsymbol {x}}}}\left(G\star \phi \right)-G\star {\frac {\partial \phi }{\partial {\boldsymbol {x}}}}\\&=&{\frac {\partial }{\partial {\boldsymbol {x}}}}\int _{{\Omega }}G({\boldsymbol {x}}-{\boldsymbol {r}},\Delta ({\boldsymbol {x}},t))\phi ({\boldsymbol {r}},t)d{\boldsymbol {r}}-G\star {\frac {\partial \phi }{\partial {\boldsymbol {x}}}}\\&=&\left({\frac {\partial G}{\partial \Delta }}\star \phi \right){\frac {\partial \Delta }{\partial x}}+\int _{{d\Omega }}G(x-r,\Delta (x,t))\phi (r,t){\boldsymbol {n}}dS\end{array}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e57745aa7084e0d0022df94ab931e87a98445e8)
서n {\은 \ \ 및
\ \ 및 의 표면에 수직인 벡터입니다 d\. }
의 표면에 수직인 벡터입니다 d\. }
이 두 항은 둘 다 불균일성으로 인해 나타납니다.첫 번째는 필터 크기 \ \ \displaystyle, \displaystyle \Delta.로 필터 G G와
\displaystyle, \displaystyle \Delta.로 필터 G G와 시간적 도함수의 교락은 필터 크기의 시간적 변화로 인한 오차항으로 이어진다.
시간적 도함수의 교락은 필터 크기의 시간적 변화로 인한 오차항으로 이어진다.
![\left[{\frac {\partial }{\partial t}},G\star \right]=\left({\frac {\partial G}{\partial \Delta }}\star \phi \right){\frac {\partial \Delta }{\partial t}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/924c69bb805ddb80ca5ad23979fb9d5c77c964ac)
이러한 오류 용어를 제거하거나 최소화하는 필터 연산이 제안되었습니다.[citation needed]
고전적인 대형 와류 시뮬레이션 필터
![[icon]](//upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | 이 섹션은 플롯의 적절한 정렬을 사용하여 확장해야 합니다.추가해서 도움을 드릴 수 있습니다. (2020년 1월) |
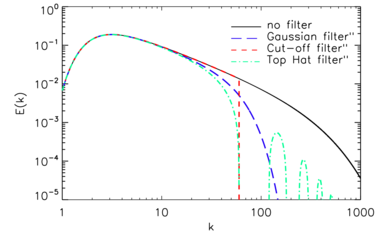
일반적으로 대형 와류 시뮬레이션에서 공간 필터링에 사용되는 세 가지 필터가 있습니다.G( ,) { G ( { \ symbol {} , } ) G( ,)), { { ( { \ symbol { , \ } )의
G( ,)), { { ( { \ symbol { , \ } )의 정의와 중요한 속성에 대한 설명이 [2]제시되어 있습니다.
정의와 중요한 속성에 대한 설명이 [2]제시되어 있습니다.
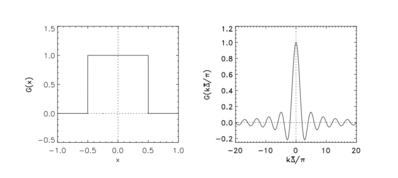
박스 필터
물리적 공간의 필터 커널은 다음과 같이 제공됩니다.

스펙트럼 공간의 필터 커널은 다음과 같이 주어진다.

가우스 필터
물리적 공간의 필터 커널은 다음과 같이 제공됩니다.

스펙트럼 공간의 필터 커널은 다음과 같이 주어진다.

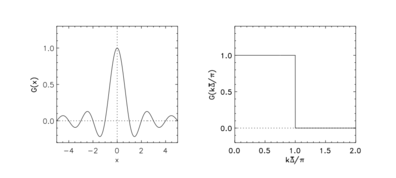
물리적 및 스펙트럼 공간의 날카로운 스펙트럼 필터 샤프 스펙트럼 필터
물리적 공간의 필터 커널은 다음과 같이 제공됩니다.

스펙트럼 공간의 필터 커널은 다음과 같이 주어진다.

「 」를 참조해 주세요.
레퍼런스




 사용되는 필터 유형에 고유한 컨볼루션 커널입니다.이는 컨볼루션 연산이라고 할 수 있습니다.
사용되는 필터 유형에 고유한 컨볼루션 커널입니다.이는 컨볼루션 연산이라고 할 수 있습니다.
 컷오프 길이와 시간 스케일을 사용합니다.
컷오프 길이와 시간 스케일을 사용합니다.











 컷오프 주파수
컷오프 주파수 







![[f,g]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6d19d70e6a63d3650c33b1e58d1f69bbb956072) 대해 연산자
대해 연산자![[f,g]\phi =f\circ g(\phi )-g\circ f(\phi )=f(g(\phi ))-g(f(\phi )),](https://wikimedia.org/api/rest_v1/media/math/render/svg/c16f02f51de3e6ea23348440769390f4ee0e1ea5)
![\left[G\star ,{\frac {\partial }{\partial s}}\right]=0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ffc45070eaa4ca1d242e99c812ab5cb6d39c772)


![{\begin{array}{rcl}\left[{\frac {\partial }{\partial {\boldsymbol {x}}}},G\star \right]\phi &=&{\frac {\partial }{\partial {\boldsymbol {x}}}}\left(G\star \phi \right)-G\star {\frac {\partial \phi }{\partial {\boldsymbol {x}}}}\\&=&{\frac {\partial }{\partial {\boldsymbol {x}}}}\int _{{\Omega }}G({\boldsymbol {x}}-{\boldsymbol {r}},\Delta ({\boldsymbol {x}},t))\phi ({\boldsymbol {r}},t)d{\boldsymbol {r}}-G\star {\frac {\partial \phi }{\partial {\boldsymbol {x}}}}\\&=&\left({\frac {\partial G}{\partial \Delta }}\star \phi \right){\frac {\partial \Delta }{\partial x}}+\int _{{d\Omega }}G(x-r,\Delta (x,t))\phi (r,t){\boldsymbol {n}}dS\end{array}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e57745aa7084e0d0022df94ab931e87a98445e8)



![\left[{\frac {\partial }{\partial t}},G\star \right]=\left({\frac {\partial G}{\partial \Delta }}\star \phi \right){\frac {\partial \Delta }{\partial t}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/924c69bb805ddb80ca5ad23979fb9d5c77c964ac)

 정의와 중요한 속성에 대한 설명이
정의와 중요한 속성에 대한 설명이