일반 틀

이 글에는 여러 가지 문제가 있다.이 문제를 개선하거나 대화 페이지에서 토의하십시오.(이러한 템플릿 메시지를 제거하는 방법 및 시기 알아보기) 이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "일반 프레임" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2020년 11월) (이 템플릿 메시지를 제거하는 방법과 시기 학습) 이 글에는 참고문헌, 관련 독서 또는 외부 링크 목록이 수록되어 있으나 인라인 인용구가 부족하여 출처가 불분명하다. 좀 더 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오.(2020년 11월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

논리학에서 일반 프레임(또는 단순 프레임)은 추가 구조를 가진 Kripke 프레임으로, 모달 및 중간 로직의 모델링에 사용된다.일반적인 프레임 의미론들은 크립케 의미론과 대수적 의미론들의 주요 덕목을 결합한다: 그것은 전자의 투명한 기하학적 통찰과 후자의 견고한 완성도를 공유한다.

정의

A modal general frame is a triple ${\displaystyle \mathbf {F} =\langle F,R,V\rangle }$, where ${\displaystyle \langle F,R\rangle }$ is a Kripke frame (i.e., R is a binary relation on the set F), and V is a set of subsets of F that is closed under the following:

• (이진) 교차로, 유니언 및 보어의 부울 연산
• $◻{\displaystyle }$ ${\displaystyle A}$=${\displaystyle }${ x ${\displaystyle \in }$ ${\displaystyle F;}$$$${\displaystyle \forall \mathrm{}}$ ${\displaystyle y}$ ${\displaystyle \in }$ ${\displaystyle F}$( x ${\displaystyle R}$ y${\displaystyle }$→ y ${\displaystyle \in }$ ${\displaystyle A)\}}$ ${\displaystyle \box$ A$=\{x\in F;\,\all y\in F\,$ ($x\,R\,y\to,y\$$to$ y$\)\$로 정의된 작업$.$

따라서 그들은 추가적인 구조를 가진 집합의 특별한 경우다.V의 목적은 프레임에 허용되는 평가를 제한하는 것이다: ${\displaystyle \mathrm{크립케}}$ 프레임 $⟨{\displaystyle }$ ${\displaystyle F}$${\displaystyle }$, $R$,${\displaystyle ⊩}$ ${\displaystyle ⟩}$ \ $\$ \ \ \ $F$ ,${\displaystyle R}$ ${\displaystyle ⟩}$ { { ${$$$\$dash$ \$rangle }이(가$) 일반 프레임 F에서 허용된다.

${\displaystyle \mathrm{모든}}$ 명제 변수 p에 ${\displaystyle 대해}$${\displaystyle }${ x ${\displaystyle \in }$ ${\displaystyle F;}$ x ${\displaystyle ⊩}$ ${\displaystyle p}$ ${\displaystyle \}}$ ${\displaystyle V}$ ${\displaystyle \{x\in$ F$;\,x\Vdash p\}\in V}.$

그런 다음 V의 폐쇄 조건은 모든 공식 A(변수뿐만 아니라${\displaystyle )}$에 대해 V에${\displaystyle \mathrm{속하는지}}$ 확인하십시오$.$ $displaystyle \{x\in F;\,x\Vdash A\}}$이(가) V에 속하는지$$ 확인하십시오.

A formula A is valid in F, if ${\displaystyle x\Vdash A}$ for all admissible valuations ${\displaystyle \Vdash }$, and all points ${\displaystyle x\in F}$. A normal modal logic L is valid in the frame F, if all axioms (or equivalently, all theorems) of L are valid in F.이 경우에 우리는 F를 L-프레임이라고 부른다.

A Kripke frame ${\displaystyle \langle F,R\rangle }$ may be identified with a general frame in which all valuations are admissible: i.e., ${\displaystyle \langle F,R,{\mathcal {P}}(F)\rangle }$, where ${\displaystyle {\mathcal {P}}(F)}$ denotes the power set of F.

프레임의 종류

일반적으로 일반 프레임은 Kripke 모델의 화려한 이름 이상일 수 없으며, 특히 접근성 관계에 대한 속성에 대한 모달 공리의 일치성은 상실된다.이는 허용 가능한 평가 집합에 추가 조건을 부과함으로써 해결할 수 있다.

프레임 $F{\displaystyle \mathbf{}}$= ${\displaystyle ⟨}$ ${\displaystyle F}$, ${\displaystyle R}$, ${\displaystyle V}$ ${\displaystyle ⟩}$ ${\displaystyle \mathbf {F} =\langle F,R,V\angle }$을(를) 호출한다$$.

• 구별되는 ${\displaystyle \mathrm{경우}}$,${\displaystyle \mathrm{}\in }$ A ${\displaystyle (}$ ${\displaystyle V}$ ${\displaystyle (x}$ ${\displaystyle y}$A ${\displaystyle y}$y ${\displaystyle )}$ ${\displaystyle A}$ ) {\$all A\in$ V$\, (x\in$A$\Leftrightarrow$ y$\in A)}$에서 $x{\displaystyle }$= ${\displaystyle y}$ ${\displaysty$ x$=y$
• 타이트한 ${\displaystyle \mathrm{경우}}$, $\forall {\displaystyle \mathrm{}}$A ${\displaystyle (}$ ${\displaystyle V}$ (${\displaystyle x}$ ${\displaystyle ◻}$ ${\displaystyle y}$A ${\displaystyle y}$y ${\displaystyle )}$ ${\displaystyle A}$ ) ${\displaystyle \for all$A$\in$ V$\(x\in$ \$Box$A\$Rightarrow y\in$ A$)}$이(${\displaystyle 가}$) x$$R {\$displaystysty x\,R$\,y$$}을 의미하며$,$$y}$은 다음과 같다.
• 압축, 유한 교차 특성을 가진 V의 모든 부분 집합이 비어 있지 않은 교차점을 갖는 경우,
• 원자, V가 단골격을 모두 포함하면
• 정제, 차별화, 조여진다면
• 정교하고 압축된 경우 기술적으로 설명해야 한다.

크립크 틀은 정제되고 원자적이다.그러나 무한의 크립키 프레임은 결코 소형화되지 않는다.모든 유한한 차별화 또는 원자 프레임은 크립케 프레임이다.

서술형 프레임은 이중성 이론 때문에 프레임의 가장 중요한 등급이다(아래 참조).정제된 프레임은 서술형 프레임과 크립키 프레임의 일반적인 일반화로 유용하다.

프레임의 작동 및 형태

${\displaystyle \mathrm{모든}}$ Kripke 모델 $⟨{\displaystyle }$ ${\displaystyle F}$, R ,${\displaystyle ⊩}$ ${\displaystyle ⟩}$ \${\displaystyle$ \$langle$ F$,$${\displaystyle R}$$,{\Vdash }\langle }}$은(는) ${\displaystyle \mathrm{일반}}$ 프레임 $⟨{\displaystyle }$ F${\displaystyle }$, R${\displaystyle ,}$ ${\displaystyle V}$ ${\displaystyle ⟩}$ ${\displaystyle \langle F,R,V\rangele}$을 유도하며, 여기서 V는 V로 정의된다$.$

${\displaystyle V={\big \{}\{x\in F;\,x\vdash A\};\,A{\hbox{은 공식}{\big \}}}}.}$

생성된 서브프레임, p-모르픽 영상 및 Kripke 프레임의 불연속 조합의 기본적인 진실 보존 운영은 일반 프레임에서 유사하다.A frame ${\displaystyle \mathbf {G} =\langle G,S,W\rangle }$ is a generated subframe of a frame ${\displaystyle \mathbf {F} =\langle F,R,V\rangle }$, if the Kripke frame ${\displaystyle \langle G,S\rangle }$ is a generated subframe of the Kripke frame ${\displaystyl$$e{\displaystyle }$ $\langle F,R\rangele }($즉, $G{\displaystyle }$ ${\displaystyle G}$은$($는) $R{\displaystyle }$ ${\displaystyle R}$에서 위쪽으로${\displaystyle \mathrm{닫힌}}$ $F{\displaystyle }$ ${\displaystyle$ ${\displaystyle F}$$}$의 하위 집합이며, S = R ×${\displaystyle G}$ ${\displaystyle S=R\cap G\time G}$이다.)$$ 및

$W=\{A\cap G;\,A\in V\}}$

A p-morphism (or bounded morphism) ${\displaystyle f\colon \mathbf {F} \to \mathbf {G} }$ is a function from F to G that is a p-morphism of the Kripke frames ${\displaystyle \langle F,R\rangle }$ and ${\displaystyle \langle G,S\rangle }$, and satisfies the additional constraint

${\displaystyle {}^{}}$${\displaystyle f}$${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$[ ${\displaystyle A}$ ${\displaystyle ]}$ ${\displaystyle \in }$ ${\displaystyle V}$ ${\displaystyle$ f$^{1}[A]-\in$ V$}$ 모든$$ $A{\displaystyle }$ ${\displaystyle \in }$ W ${\displaystyle A\in W$

The disjoint union of an indexed set of frames ${\displaystyle \mathbf {F} _{i}=\langle F_{i},R_{i},V_{i}\rangle }$, ${\displaystyle i\in I}$, is the frame ${\displaystyle \mathbf {F} =\langle F,R,V\rangle }$, where F is the disjoint union of ${\displaystyle \{F_i;i}$${\displaystyle \in }$ ${\displaystyle I\}}$ ${\displaystyle \{F_{i};\,i\in$ I$\backslash \},$ R은${\displaystyle }${${\displaystyle {Ri}_{}}$ ${\displaystyle I}$ ${\displaystyle \in }$ ${\displaystyle I\}}$ ${\displaystyle \{R_{i};\,i\}$의 조합이며$,$

${\displaystyle V=\{A\subseteq F;\,\all I\, (A\cap F_{i}\in V_{i}\}).}$

The refinement of a frame ${\displaystyle \mathbf {F} =\langle F,R,V\rangle }$ is a refined frame ${\displaystyle \mathbf {G} =\langle G,S,W\rangle }$ defined as follows.우리는 동등성 관계를 고려한다.

$(x\displaystyle x\sim y\iff \all A\in V\, (x\in A\Leftrightarrow y\in A))}$

$그리고{\displaystyle }$ G${\displaystyle }$= ${\displaystyle F}$/${\displaystyle }$~ ${\$을$({\displaystyle }$를) ~ ${\displaystyle \sim }$의 동등성 클래스의 집합으로$$ 한다$.$ 그런 다음,

${\displaystyle \langle x/{\sim }y/{\sim }\in S\iff \f \f forall A\in V\, (x\in \Box A\Rightarrow y\in),}$

$A/{\sim }\in W\iff A\in V.}$

완성도

Kripke 프레임과는 달리, 모든 정상적인 모달 논리 L은 일반 프레임의 클래스에 관하여 완전하다.This is a consequence of the fact that L is complete with respect to a class of Kripke models ${\displaystyle \langle F,R,{\Vdash }\rangle }$: as L is closed under substitution, the general frame induced by ${\displaystyle \langle F,R,{\Vdash }\rangle }$ is an L-frame.더욱이 모든 논리 L은 하나의 서술적 틀에 관해서 완전하다.실제로 L은 그 규범적 모델에 관해서 완전하며, 규범적 모델(L의 규범적 프레임이라고 함)에 의해 유도된 일반적 프레임은 서술적이다.

욘손-타르스키 이중성

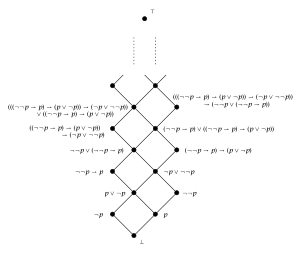
일반 프레임은 모달 알헤브라와 밀접한 관련이 있다.${\displaystyle \mathrm{Let}}$ $F{\displaystyle \mathbf{}}$= ${\displaystyle ⟨}$ F${\displaystyle }$, ${\displaystyle R}$, ${\displaystyle V}$ ${\displaystyle ⟩}$ ${\displaystyle \mathbf {F} =\langle F,R,V\angle }$은(는) 일반적인 프레임이다$$.The set V is closed under Boolean operations, therefore it is a subalgebra of the power set Boolean algebra ${\displaystyle \langle {\mathcal {P}}(F),\cap ,\cup ,-\rangle }$. It also carries an additional unary operation, ${\displaystyle \Box }$. The combined structure ${\display$$스타일 \langle V,\cap,\cup,-,\Box \rangle$}}은$($는) 모달 대수학으로$$ F의 이중 대수라고 하며 $F{\displaystyle {\mathbf{}}^{}}$ +${\$ {$F} ^{+}}$로 표시된다$.$

In the opposite direction, it is possible to construct the dual frame ${\displaystyle \mathbf {A} _{+}=\langle F,R,V\rangle }$ to any modal algebra ${\displaystyle \mathbf {A} =\langle A,\wedge ,\vee ,-,\Box \rangle }$. The Boolean algebra ${\displaystyle \lang$$Le A,\wedge,\vee,-\rangele }$에는 스톤 공간이 있으며$$, 그 기본 집합 F는 A의 모든 초여광 필터의 집합이다.$A{\displaystyle {\mathbf{}}_{}}$+ ${\$에 허용되는 가치의 V 집합은 F의 열린 하위 집합으로 구성되며$$, 접근성 관계 R은 다음과 같이 정의된다.

$\displaystyle x\,R\,y\iff \fall a\in a\,(\Box a\in x\Rightarrow a\in y)}$

모든 울트라필터용 x와 y.

프레임과 프레임의 이중은 동일한 공식을 검증하므로 일반적인 프레임 의미론과 대수적 의미론은 어떤 의미에서 동등하다.모든 모달 대수의 이중$$ 이중$({\displaystyle {}_{}}$+${\displaystyle {}_{}{}^{}}$)${\displaystyle {}^{}}$+ ${\$은 그 $자체$로$$A {\$displaystyle$ \$mathbf {A}$에 이형적이다.모든 대수의 이중은 서술적이기 때문에 프레임의 이중의 경우 일반적으로 이것은 사실이 아니다.실제로 $프레임{\displaystyle \mathbf{}}$ F$${\$displaystyle \mathbf {F}}$은(는$)$ 이중${\displaystyle {(}_{}}$F$$+ ) + {\$displaystyle$(\$mathbf$ {F}$^{+}_{+}}})$에 대해 이형인 경우에만 설명된다$.$

p-모형성의 이중성을 한 편으로는 정의할 수 있고, 다른 한편에서는 모달 대수 동형성의 이중성을 정의할 수도 있다.이렇게 하여 연산자${\displaystyle (\cdot {}^{}}$)${\displaystyle {}^{}}$+ ${\$ ${\displaystyle (\cdot {}_{}}$)${\displaystyle {}_{}}$+ ${\$는 일반 프레임의 범주, 모달 알헤브라의 범주 사이에 한 쌍의 상반된 펑커가 된다$$.이러한 functors는 서술형 프레임과 모달 알헤브라의 범주 사이에 이중성(Bjarni Jonsson과 Alfred Tarski의 이름을 따서 Jonsson-Tarski라고 함)을 제공한다.이것은 복잡한 알헤브라와 관계 구조물의 세트장 사이에 더 일반적인 이중성의 특별한 경우다.

직감 프레임

직관적 및 중간 로직의 프레임 의미론은 모달 로직의 의미론과 병렬로 개발될 수 있다.직관적인 일반 프레임은 3중 $⟨{\displaystyle }$ ${\displaystyle F}$, ${\displaystyle \le }$, ${\displaystyle V}$ ${\displaystyle ⟩}$ ${\displaystyle \langle$ F$,\leq ,V\rangele }$이며$,$ 여기서 $\le {\displaystyle }$ ${\displaystyle \leq }$은 F의 부분적인 주문이며$$, V는 빈 세트를 포함하는 F의 상부 서브셋(콘) 집합이며, 아래에서 닫힌다.

• 교차로와 조합,
• 작업 $A{\displaystyle }$→ ${\displaystyle B}$ =${\displaystyle ◻}$(${\displaystyle }$- ${\displaystyle A}$ ${\displaystyle \cup }$ B${\displaystyle }$) ${\displaystyle A\to$ B$=\Box(-A\cup B$

타당성 및 기타 개념은 모달 프레임과 유사하게 도입되며, 허용 가능한 평가 집합의 취약한 폐쇄 특성을 수용하기 위해 몇 가지 변경이 필요하다.특히 직감 프레임 $F{\displaystyle \mathbf{}}$= ${\displaystyle ⟨}$ ${\displaystyle F}$, ${\displaystyle \le }$, ${\displaystyle V}$ ${\displaystyle ⟩}$ ${\displaystyle \mathbf {F} =\langle F,\leq ,V\rangele }$을(를) 부른다.

• ${\displaystyle \mathrm{tight}}$ A ${\displaystyle \in }$ ${\displaystyle V}$ ${\displaystyle (x}$ ${\displaystyle \in }$ ${\displaystyle A}$ ${\displaystyle \iff }$ ${\displaystyle y}$ ${\displaystyle \in }$ ${\displaystyle A}$) ${\all A\in V\$에 대해 \$displaystyle$\for \$frontrightarrow$ y$\in$ A)}이$(가$) $x{\displaystyle }$ ${\displaystyle \le }$ ${\displaystyle y}$ ${\displaysty x\leq$ y$}$을 의미한다면$,$
• 콤팩트, 유한 교차로 속성이 있는$$ $V{\displaystyle }$ ${\displaystyle \cup \{F}$- ${\displaystyle A;}$ ${\displaystyle A}$ ${\displaystyle \in }$ ${\displaystyle V}$ ${\displaystyle \}}$ ${\displaystyle$ V$\cup \{F-A;\,A\in$ V$\}}$의 모든 부분 집합이 비어 있지 않은 교차점을 갖는 경우.

촘촘한 직감 프레임은 자동으로 차별화돼 정교해진다.

The dual of an intuitionistic frame ${\displaystyle \mathbf {F} =\langle F,\leq ,V\rangle }$ is the Heyting algebra ${\displaystyle \mathbf {F} ^{+}=\langle V,\cap ,\cup ,\to ,\emptyset \rangle }$. The dual of a Heyting algebra ${\displaystyle \mathbf$${A} =\langle A,\wedge ,\vee ,\to ,0\rangle }$ is the intuitionistic frame ${\displaystyle \mathbf {A} _{+}=\langle F,\leq ,V\rangle }$, where F is the set of all prime filters of A, the ordering ${\displaystyle \leq }$ is inclusion, and V consists of all subsets of F of the form

${\displaystyle \{x\in F;\,a\in x\}}$

$여기$서 ${\displaystyle \in }$ ${\displaystyle A}$ ${\displaystyle a\in$ A$\}.$ 모달 케이스에서처럼 ${\displaystyle (\cdot {}^{}}$)${\displaystyle {}^{}}$+ ${\$${\displaystyle {}_{}}$+ ${\$은 반투명 펑커의 한 쌍으로$$, 헤이팅알헤이스트레이브라의 범주를 기술직주의 프레임의 범주와 사실상 동일하다.

전이적 반사적 모달 프레임에서 직관적 일반 프레임을 구성할 수 있으며, 그 반대의 경우도 모달 동반자를 참조한다.

참조

• 알렉산더 차그로프와 마이클 자카리아셰프, 모달 로직, 옥스퍼드 대학 출판부, 1997년 옥스퍼드 로직 가이드 35권.
• 2001년 캠브리지 대학 출판부의 이론 컴퓨터 과학의 패트릭 블랙번, 마아텐 드 리케, 그리고 모달 로직 이데 베네마, 모달 로직, 케임브리지 대학 출판부의 이론 컴퓨터 과학의 53권.