히그만-심스 그래프

Higman–Sims graph
히그만-심스 그래프
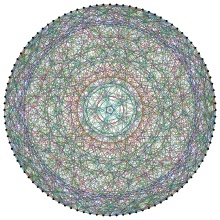Higman Sims Graph.svg
Paul R을 바탕으로 그린 그림.하프너의 공사.[1]
이름을 따서 명명됨도널드 G.히그만
찰스 C.심스
정점100
가장자리1100
반지름2
지름2
둘레4
자동형성88,704,000 (HS:2)
특성.강력정규
에지 변환
해밀턴어
오일러어
그래프 및 모수 표
하프너 건설의 분리된 부분들.

수학 그래프 이론에서 히그만-심스 그래프는 정점 100개와 가장자리 1100개를 가진 22개의 정규 비방향 그래프다.인접 쌍의 정점이 공통 이웃을 공유하지 않고 각 비근접 쌍의 정점 쌍이 6개의 공통 이웃을 공유하는 고유한 정규 그래프 srg(100,22,0,6)이다.[2]메스너(1956년)가 처음 건설했고 1968년 도널드 G가 재발견했다.히그만과 찰스 C.Sims는 Higman-Sims 그룹을 정의하기 위한 방법으로, Higman-Sims 그룹의 자동화 그룹에서 지수 2의 하위그룹이다.[3]

건설

M22 그래프에서

M22 그래프, 매우 정규적인 그래프 srg(77,16,0,4)를 취하여 S(3,6,22)의 점에 해당하는 22개의 정점, 각 블록이 그 점에 연결되는 22개의 새로운 정점, 22점에 연결된 1개의 정점 C로 증가시킨다.

From Hoffman-Singleton 그래프

호프만-싱글턴 그래프에는 크기 15의 독립형 세트 100개가 있다.100개의 해당 정점이 있는 새 그래프를 만들고, 해당 독립 집합이 정확히 0 또는 8개의 요소를 공통으로 갖는 정점을 연결한다.결과적인 Higman-Sims 그래프는 352가지 방법으로 Hoffman-Singleton 그래프의 두 복사본으로 분할할 수 있다.

큐브에서

000, 001, 010, ..., 111이라는 정점이 있는 큐브를 취한다.70개의 가능한 4-set의 정점만 유지하고 XOR가 000으로 평가되는 정점만 유지하십시오. 이러한 4-set은 6면 + 6 대각선 사각형 + 2 패리티 4-setra에 해당하는 14개입니다.이는 8개 지점에 3-(8,4,1) 블록 설계로, 블록 크기 4의 블록 14개가 각각 7개 블록으로 나타나며, 각 한 쌍의 점이 3회씩 나타나며, 각 점의 3배는 정확히 한 번 발생한다.원래 8 정점을 8! = 40320방향으로 허용하고 중복된 정점은 폐기하십시오.그리고 정점에 다시 라벨을 붙이는 30가지 방법(즉, 점의 순열에 의해 서로 모두 이형화된 30가지 설계)이 있다.1344개의 자동형이 있고, 40320/1344 = 30이 있기 때문이다.

30개의 설계 각각에 대해 그리고 모든 설계의 각 행에 대해 꼭지점을 만드십시오(총 70개의 해당 행이 있으며, 각 행은 4-set 8이고 6개의 설계에 표시됨).각 설계를 14개의 행에 연결하십시오.분리 설계(각 설계는 다른 8개 설계와 분리됨)를 서로 연결하십시오.같은 요소가 정확히 하나 있다면 행을 서로 연결하십시오(4x4 = 16 그러한 인접 요소가 있음).결과 그래프는 Higman-Sims 그래프다.행은 16개의 다른 행과 6개의 설계 == 도 22에 연결된다.설계는 14개의 행과 8개의 불연속 설계 == 도 22에 연결된다.따라서 100개의 꼭지점들은 각각 22도를 가진다.

대수적 특성

히그만-심스 그래프의 자동형 집단은 히그만-심스 그룹의 반간접 생산물에 대해 8870만4천개의 이형집단을 순서 2의 순환집단을 갖는 그룹이다.[4]그것은 어떤 다른 가장자리에도 도달하는 자동화 기능을 가지고 있어, Higman-Sims 그래프를 가장자리 변환 그래프로 만든다.[5]

Higman-Sims 그래프의 특성 다항식은 (x - 22)(x - 2)(77x + 8)이다.22따라서 Higman-Sims 그래프는 정수 그래프로서 스펙트럼은 전적으로 정수로 구성된다.또한 이 특성 다항식을 가진 유일한 그래프로, 스펙트럼에 의해 결정되는 그래프가 된다.

리치 격자 내부

리치 격자 내부의 히그만-심스 그래프의 투영.

The Higman–Sims graph naturally occurs inside the Leech lattice: if X, Y and Z are three points in the Leech lattice such that the distances XY, XZ and YZ are respectively, then there are exactly 100 Leech lattice points T such that all the distances XT, YT and ZT are equal to 2, and 이들 사이의 거리가 일 때 두 개의 그러한 점 T와 T′을 연결하면 결과 그래프가 Higman-Sims 그래프에 이형화된다또한 X, Y, Z를 각각 고정하는 리치 격자(즉, 이를 고정하는 유클리드 화합물)의 모든 자동화 집합은 히그만-심스 그룹이다(X와 Y를 교환할 수 있으면 모든 그래프 자동화의 순서 2 확장이 얻어진다).이는 히그만-심스 그룹이 콘웨이 그룹 Co2(주문 2 확장)와 Co, 그리고3 결과적으로 Co에서1 발생한다는 것을 보여준다.[6]

참조

  1. ^ Hafner, P. R. (2004). "On the Graphs of Hoffman–Singleton and Higman–Sims" (PDF). the Electronic Journal of Combinatorics. 11 (1): R77(1–32). doi:10.37236/1830.{{cite journal}}: (도움말)의 외부 링크
  2. ^ Weisstein, Eric W. "Higman–Sims Graph". MathWorld.
  3. ^ Higman, Donald G.; Sims, Charles C. (1968). "A simple group of order 44,352,000" (PDF). Mathematische Zeitschrift. 105 (2): 110–113. doi:10.1007/BF01110435. hdl:2027.42/46258..
  4. ^ Brouwer, Andries E. "Higman–Sims graph".
  5. ^ 브루워, A. E.와 해머, W. H. "게위츠 그래프: 그래프 스펙트럼 이론의 연습"유로. J. 콤빈. 14, 397–407, 1993.
  6. ^ Conway, John H.; Sloane, Neil J. A. Sphere Packings, Lattices and Groups. Grundlehren der mathematischen Wissenschaften (3rd ed.). Springer-Verlag. ISBN 1-4419-3134-1. 제10장(John H. Conway, "특출한 그룹에 대한 세 개의 강의"), §3.5("The Higman-Sims and McLaughlin 그룹"), 페이지 292–293.
  • Mesner, Dale Marsh (1956), An investigation of certain combinatorial properties of partially balanced incomplete block experimental designs and association schemes, with a detailed study of designs of Latin square and related types, Doctoral Thesis, Department of Statistics, Michigan State University, MR 2612633