더미 변수(통계)

통계와 계량학, 특히 회귀 분석에서 더미 변수는^[a] 결과를 변화시킬 것으로 예상할 수 있는 어떤 범주형 효과의 부재 또는 존재를 나타내기 위해 값 0 또는 1만 취하는 변수다.^[2][3] 그것들은 데이터를 흡연자와 비흡연자와 같이 상호 배타적인 범주로 분류하면서 회귀 모델에서 질적 사실에 대한 숫자적 스탠드로 생각할 수 있다.^[4]

일부 관측치의 값이 0인 더미 독립 변수(더미 설명 변수라고도 함)는 더미가 값 1을 인수할 때 그 계수가 절편을 변경하기 위해 작용하는 동안 해당 변수의 계수가 종속 변수에 영향을 미치는 역할을 하지 못하게 한다. 예를 들어 그룹의 멤버십이 회귀와 관련된 질적 변수 중 하나라고 가정해 보십시오. 만약 그룹 멤버쉽이 임의로 1의 값을 할당한다면, 다른 모든 멤버들은 0의 값을 얻게 될 것이다. 그런 다음 절편은 비회원의 상수 항이지만, 그룹 멤버의 경우 멤버쉽 더미의 계수를 더한 상수 항이 될 것이다.^[5]

더미 변수는 시스템 스위칭, 계절 분석 및 정성적 데이터 적용과 함께 시계열 분석에서 자주 사용된다.

더미 독립형 통합

더미 변수는 회귀 모형에 (설명 변수로) 포함된 양적 변수와 같은 방식으로 통합된다. 예를 들어, 임금 결정의 Mincer형 회귀 모델을 고려할 때, 임금은 성별(정량적)과 교육연수(정량적)에 따라 달라진다.

${\displaystyle \ln {\text{warden}=\reason_{0}+\reason_{0}{\text{women}\reason_{1}{\text{교육}+u}$

여기서 $u{\displaystyle }$~ ${\displaystyle N}$( ${\displaystyle 0}$ ,${\displaystyle {\sigma \mathrm{}}^{}}$ 2${\displaystyle {}^{}}$) ${\displaystyle u\sim N(0,\sigma ^{2$})은$$오류 용어다. 모형에서, 여자가 여자일 때는 1이고, 여자가 남자일 때는 0이다. ${\displaystyle {\Delta }_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$은 교육을 일정하게 유지하는 여성과 남성의 임금 차이로 해석할 수 있다$$. 따라서 Δ는₀ 남성과 여성 사이에 임금에 차별이 있는지를 판단하는 데 도움이 된다. 예를 들어 Δ₀>0(양수 계수)이 되면, 여성이 남성보다 더 높은 임금을 받는다(다른 요인을 일정하게 유지). 더미 변수에 부착된 계수를 미분 절편 계수라고 한다. 이 모델은 여성과 남성 사이의 가로채기 이동으로 그래픽으로 묘사될 수 있다. 이 수치에는 (남성이 여성보다 더 높은 임금을 받는) Δ₀<0이 표시된다.^[6]

더미 변수는 더 복잡한 경우로 확장될 수 있다. 예를 들어, 계절 효과는 각 계절에 대한 더미 $변수$를 생성하여 포착할 수 있다: D${\displaystyle {}_{}}$1 = ${\displaystyle 1}$ $[\displaystyle D_{1}=1}$ 관측치가 여름용이고 그렇지 않으면 0인 경우$$ $D{\displaystyle {}_{}}$ ${\displaystyle 2{}_{}}$= 1 ${\displaystyle D_{2}=1},$ 그렇지 않으면 0인 경우$$ D ${\displaystyle {3\mathrm{}}_{}}$= 1 ${\displaystystyle D_{3}=1$}=$}$만 해당된다$$. 겨울인 경우, 그렇지 않으면 0이고, 봄인 ${\displaystyle {경우}_{}}$에만 D ${\displaystyle 4{}_{}}$= 1 ${\displaystyle D_{4}=1}.$ 패널 데이터에서 고정 효과 추정기 더미는 단면 데이터(예: 회사 또는 국가) 또는 풀링된 시계열에서 각 단위에 대해 생성된다. 단, 그러한 퇴행에서는 상수 항을 제거하거나 더미 중 하나를 제거해야 하며, 관련 범주는 더미 변수 트랩을 피하기 위해 다른 범주가 평가되는 기본 범주가 된다.

모든 회귀 방정식의 상수 항은 1과 동일한 회귀 방정식을 곱한 계수다. 회귀가 행렬 방정식으로 표현되는 경우, 회귀 분석기의 행렬은 한 열(상수 항), 0과 1의 벡터(더미) 및 다른 회귀 분석기로 구성된다. 만약 어떤 사람이 남성과 여성 인체모형을 모두 포함한다면, 예를 들어, 모든 관찰은 남성 또는 여성으로 분류되기 때문에 이 벡터의 합은 하나의 벡터다. 따라서 이 합은 상수 항의 퇴행인 1의 첫 번째 벡터와 같다. 그 결과, 회귀 방정식은 일반적인 의사역전법에 의해서도 해석할 수 없을 것이다. 즉, 원점 벡터(정수 용어) 리렉터와 모든 인체모형의 집합이 모두 존재하면 완벽한 다중 공선성이 발생하며,^[7] 회귀에 의해 형성된 방정식의 시스템에는 고유한 해법이 없다. 이것을 더미 변수 트랩이라고 한다. 이 함정은 상수 용어 또는 불쾌감을 주는 더미 중 하나를 제거함으로써 피할 수 있다. 제거된 더미는 다른 범주를 비교하는 기본 범주가 된다.

분산 분석 모형

종속 변수가 본질적으로는 양적이지만 모든 설명 변수가 더미(본질에서는 양적)인 회귀 모형을 분산 분석(ANOVA) 모형이라고 한다.^[4]

정성적 변수가 하나인 분산 분석 모형

공립학교 교사의 평균 연봉이 (1) 북방(21개 주) (2) 남방(17개 주) 서방(13개 주)의 51개 주에 있는 국가 A의 3개 지리적 지역 간에 차이가 있는지 알아보기 위해 회귀 분석을 수행한다고 가정합시다. 단순 산술평균 급여는 24,424.14달러(북쪽), 22,894달러(남쪽), 26,158.62달러(서쪽)라고 한다. 산술 평균은 다르지만 통계적으로 서로 다른가? 평균 값을 비교하기 위해 분산 분석 기법을 사용할 수 있다. 회귀 모형은 다음과 같이 정의할 수 있다.

${\displaystyle {Yi}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$+ ${\displaystyle {}_{}}$ 2 ${\displaystyle {D\mathrm{}}_{}}$ ${\displaystyle 2_{}}$ ${\displaystyle {i\mathrm{}}_{}}$+ ${\displaystyle {}_{}}$ ${\displaystyle {3\mathrm{}}_{}}$ D ${\displaystyle 3_{}}$ ${\displaystyle {i\mathrm{}}_{}}$+ ${\displaystyle u_{}}$ i ${\$2}$d_{3i$}+\alpha $_{3}D_{3i}+u_{i$

어디에

${\displaystyle {Yi}_{}}$= ${\displaystyle Y_{i}=}$주 i에 있는 공립학교 교사의 평균$$ 연봉

${\displaystyle D_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle i_{}}$= ${\displaystyle 1}$ ${\displaystyle D_{2i}=1}($이(가) 북부 지역에 있는 경우$$)

${\displaystyle D_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle i_{}}$= ${\displaystyle 0}$ ${\displaystyle D_{2i}=0}($북부를 제외한 모든 지역)

${\displaystyle {}_{}}$D ${\displaystyle 3_{}}$ i${\displaystyle {}_{}}$= ${\displaystyle 1}$ ${\displaystyle D_{3i}=1}$ 상태 i가 남부 영역에 있는 경우$$

${\displaystyle D_{}}$ ${\displaystyle {3\mathrm{}}_{}}$ ${\displaystyle i_{}}$= ${\displaystyle 0}$ ${\displaystyle D_{3i}=0}$ 그렇지$$ 않으면

이 모형에서는 관측치가 특정 범주에 속할 경우 1의 값을, 다른 범주에 속할 경우 0의 값을 갖는 질적 회귀 분석만 가지고 있다. 이것은 그것을 분산 분석 모델로 만든다.

이제 쌍방의 기대를 받아 다음과 같은 것을 얻는다.

북부지역 공립학교 교사의 평균 급여:

E(Y_i D_2i = 1, D_3i = 0) = α₁ + α₂

남부지역 공립학교 교사의 평균 급여:

E(Y_i D_2i = 0, D_3i = 1) = α₁ + α₃

서부지역 공립학교 교사의 평균 급여:

E(Y_i D_2i = 0, D_3i = 0) = α₁

(오류 항은 통상적인 OLS 조건, 즉 E(u_i) = 0을 만족한다고 가정하므로 기대 값에 포함되지 않는다.)

기대값은 다음과 같이 해석할 수 있다. 서양의 공립학교 교사의 평균 급여는 복수 회귀 방정식의 절편 용어 α와₁ 차등 절편 계수 α와₂₃ 동일하며, 남북 지역 교사의 평균 급여가 서양의 교사와 얼마나 다른지 설명한다. 따라서, 남북한 교사의 평균 급여는 서양의 교사들의 평균 급여와 비교된다. 따라서 서구는 기준 그룹 또는 벤치마크 그룹, 즉 비교가 이루어지는 그룹이 된다. 생략된 범주, 즉 더미가 할당되지 않은 범주는 기본 그룹 범주로 간주된다.

주어진 데이터를 사용하여 회귀 분석의 결과는 다음과 같다.

ŷ_i = 26,158.62 - 1734.473D_2i - 3264.615D_3i

se = (1128.523) (1435.953) (1499.615)

t = (23.1759) (-1.2078) (-2.1776)

p = (0.0000) (0.2330) (0.0349)

R² = 0.0901

여기서, se = 표준 오차, t = t-message, p = p 값

회귀 결과는 다음과 같이 해석할 수 있다. 서부지역 교사들의 평균 연봉은 약 2만6,158달러, 북한지역 교사들의 평균 연봉은 약 1734달러(2만6,158.62달러 - 1734달러)가 더 낮다.473 = 24,424.14달러, 이는 북한 교사들의 평균 연봉이다.)와 남한 교사들의 평균 연봉은 약 3265달러(2만6,158.62달러 - 3264.615달러)가 더 낮다.

남북 교사의 평균 급여가 서양의 교사와 통계적으로 다른지(비교 부문)를 알아내기 위해서는 회귀 결과의 기울기 계수가 통계적으로 유의한지 알아내야 한다. 이를 위해 p 값을 고려할 필요가 있다. 북측의 추정경사계수는 p값이 23%여서 통계적으로 유의하지 않지만 남측의 경우 p값이 3.5% 안팎에 불과해 통계적으로 유의미하지 않다. 따라서 전반적인 결과는 서구와 북부의 교사들의 평균 임금은 통계적으로 서로 다르지 않지만, 남한의 교사들의 평균 임금은 서구의 평균 임금은 약 3265달러 정도로 통계적으로 낮다는 것이다. 모델은 그림 2에 도해로 표시되어 있다. 이 모형은 하나의 질적 변수가 3개의 범주를 갖는 분산 분석 모델이다.^[4]

두 가지 정성적 변수가 있는 분산 분석 모형

분산 분석 모형에 두 가지 질적 변수가 있고, 각각 두 가지 범주가 있다고 가정합시다. 시간당 임금은 질적 변수인 '혼인 상태'(결혼/미혼)와 '지리적 지역'(북/비북)을 기준으로 설명해야 한다. 여기서, 혼인 상태와 지리적 영역이 두 개의 설명 더미 변수다.^[4]

주어진 일부 데이터에 기반한 회귀 출력이 다음과 같이 나타난다고 가정하자.

ŷ_i = 8.8148 + 1.0997D₂ - 1.6729D₃

어디에

Y = 시간당 임금(달러 단위)

D₂ = 결혼 상태, 1 = 결혼, 0 = 기타

D₃ = 지리적 영역, 1 = 북쪽, 0 = 기타

이 모델에서 단일 더미는 각 질적 변수에 할당되며, 각 변수에 포함된 범주 수보다 1개 작다.

여기서 기준 그룹은 생략된 범주: 미혼, 비북 지역 사람들이다. 모든 비교는 이 기준 그룹 또는 생략 범주와 관련하여 이루어질 것이다. 기본 범주의 시간당 평균 임금은 약 8.81달러(간격조건)이다. 이에 비해 결혼한 사람들의 시간당 평균 임금은 약 1.10달러 더 높고 약 9.91달러(8.81달러+1.10달러)에 해당한다. 이와는 대조적으로, 북한에 살고 있는 사람들의 시간당 평균 임금은 약 1.67달러 낮으며 약 7.14달러(8.81달러 - 1.67달러)이다.

일반적으로 둘 이상의 질적 변수가 회귀에 포함되는 경우 누락된 범주를 벤치마크 범주로 선택해야 한다. 모든 비교는 그 범주와 관련하여 이루어질 것이다. 절편 항은 벤치마크 범주의 기대를 나타내며 기울기 계수는 다른 범주가 벤치마크(내장) 범주와 얼마나 다른지 보여준다.^[4]

ANCOVA 모델

양적 변수와 질적 변수를 모두 포함하는 회귀 모형을 공분산 분석(ANCOVA) 모형이라고 한다. ANCOVA 모델은 분산 분석 모델의 확장이다. 이들은 양적 설명 변수(공변량 또는 제어 변수라고도 함)의 효과를 통계적으로 제어한다.^[4]

ANCOVA 모델을 형성하기 위해 질적 및 양적 회귀 분석기가 어떻게 포함되는지 설명하기 위해, A국가의 세 지역 공립학교 교사의 평균 연봉이라는 하나의 질적 변수를 가진 분산 분석 모델에서 사용되는 동일한 예를 고려한다고 가정합시다. 만약 우리가 학생당 공립학교에 대한 주정부의 지출이라는 양적 변수를 포함한다면, 우리는 다음과 같은 모델을 얻을 수 있다.

Y_i = α₁ + α₂D_2i + α₃D_3i + α₄X_i + U_i

어디에

Y_i = 주 i에 있는 공립학교 교사의 평균 연봉

X_i = 학생당 공립학교에 대한 주 지출

D_2i = 1, state i가 북부 지역에 있는 경우

D_2i = 0, 그렇지 않으면

D_3i = 1, state i가 남부 지역에 있는 경우

D_3i = 0, 그렇지 않으면

이 모형에 대한 회귀 분석 출력이

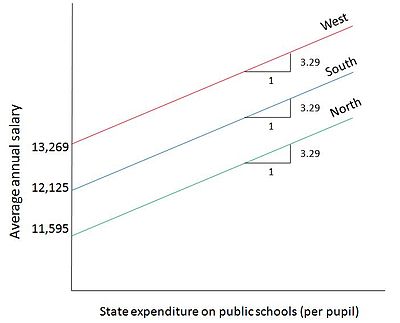
ŷ_i = 13,269.11 - 1673.514D_2i - 1144.157D_3i + 3.2889X_i

그 결과는 공립학교에 대한 학생 1인당 주 지출이 1달러 증가할 때마다 공립학교 교사의 평균 급여는 약 3.29달러씩 오른다는 것을 시사한다. 또한 북부지역의 한 주는 교사들의 평균임금이 서부지역보다 약 1673달러 낮으며, 남부지역의 한 주는 교사들의 평균임금이 서부지역보다 약 1144달러 낮다. 그림 3은 이 모델을 도식적으로 묘사하고 있다. 평균 급여 라인은 주별로 지출 계수가 달라지지 않는다는 모형의 가정으로 서로 평행하다. 각 범주에 대해 그래프에 별도로 표시된 트레이드오프(Trade off)는 두 가지 양적 변수인 공립학교 교사 급여(Y)와 공립학교 학생 1인당 국가 지출(X) 사이에 있다.^[4]

더미 변수 간의 상호작용

회귀 모형의 양적 회귀 분석기는 종종 서로 상호작용을 한다. 같은 방법으로 질적 퇴행기, 즉 더미도 서로 상호작용 효과를 가질 수 있으며, 이러한 상호작용을 회귀 모형에서 나타낼 수 있다. 예를 들어, 임금 결정을 수반하는 회귀 분석에서, 두 가지 질적 변수, 즉 성별과 결혼 여부 등을 고려한다면, 혼인 상태와 성별 사이에 상호작용이 있을 수 있다.^[6] 이러한 상호작용은 아래의 예에서와 같이 회귀 방정식에 나타낼 수 있다.

두 가지 질적 변수가 성별과 결혼 여부이고 양적 설명자가 수년간의 교육 기간인 상황에서 설명자에 있어 순전히 선형적인 회귀는 다음과 같다.

Y_i = β₁ + β₂D_2,i + β₃D_3,i + αX_i + U_i

어디에

나는 특정 개인을 가리킨다.

Y = 시간당 임금(달러 단위)

X = 교육 년수

D₂ = 여성인 경우 1, 그렇지 않은 경우 0

D₃ = 결혼한 경우 1, 그렇지 않은 경우 0

이 규격은 두 질적₃ 변수인 D와₂ D 사이에 교호작용이 발생할 가능성을 허용하지 않는다. 예를 들어, 결혼한 여성은 결혼하지 않은 남성의 그것과 다른 임금을 단지 여성일 뿐이고 결혼만 했다는 이유로 미분류의 합과 같지 않은 금액으로 벌 수 있다. 이러한 가능성을 포착하기 위해 임금의 결정을 다음과 같이 명시할 수 있다.

Y_i = β₁ + β₂D_2,i + β₃D_3,i + β₄(D_2,iD_3,i) + αX_i + U_i

여기,

β₂ = 암컷이 되는 것의 차등 효과

β₃ = 결혼의 차등 효과

β₄ = 여성 및 유부남의 추가 차이 효과

이 방정식까지가 0은 아닌 오류가 없는 경우, 결혼을 하지 않은 남성의 임금은β1+ αXi, 미혼 여성은 저것이다β1+β2+αXi, 중 결혼한 남성은β1+β3+αXi고 결혼한 여성의β1은+β2+β3+β4+ αXi(어디서의 추정치의 계수의 인체 모형 수 있게 판매했고 긍정적인, 0, 또는 )부정적인.

따라서 상호작용 인체모형(두 인체모형의 제품)은 두 인체모형을 개별적으로 고려할 때 얻는 값에서 종속 변수를 변경할 수 있다.^[4]

또는 상호작용을 포착하기 위한 더미 변수의 산물은 데이터 분류에 다른 방법(특성 조합의 관점에서 범주를 지정하는 방법)을 사용함으로써 피할 수 있다. 허락한다면

D₄ = 미혼 여성이면 1이고, 그렇지 않으면 0

D₅ = 결혼한 남자일 경우 1, 그렇지 않을 경우 0

D₆ = 기혼 여성이면 1, 그렇지 않으면 0

회귀 분석을 명시하는 것으로 충분하다.

Y_i = Δ₁ + ΔD_44,i + ΔD_55,i + ΔD_66,i + αX_i + U_i.

그 다음, 0의 충격 조건을 갖는 경우, 종속 변수의 값은 미혼 남성의 경우 Δ₁+αX_i, 미혼 여성의 경우 Δ₁+ Δ₄+ αX_i, 결혼한 여성의 경우 Δ₁₁+ Δ₅₆+ αX이다_ii. 이 규격은 교호작용 항을 사용한 이전 규격과 동일한 수의 우측 변수를 포함하며, 질적 특성의 조합에 대해 X에_i 따른 종속변수의 예측 값에 대한 회귀 결과는 이 규격과 교호작용 규격 간에 동일하다.

더미 종속 변수

종속 변수가 더미일 경우 어떻게 되는가?

더미 종속 변수(질적 종속 변수라고도 함)를 가진 모델은 설명 변수의 영향을 받은 종속 변수가 질적인 변수인 모델이다. 예를 들어, 수행 행위의 '얼마'에 관한 일부 결정은 수행 여부에 대한 사전 결정을 수반한다. "사전 결정"에 대한 회귀 분석 모델에는 종속적인 더미 변수가 있다.^[8]

예를 들어 노동력의 일부가 될 잠재적 노동자의 결정은 더미 의존 변수가 된다. 그 결정은 이분법적이다. 즉, 그 결정은 두 가지 가능한 결과를 가지고 있다: 예와 아니오. 따라서 종속적인 더미 변수 참여는 참여하면 값 1을, 참여하지 않으면 값 0을 차지한다.^[4] 이분법 종속 더미의 다른 예는 다음과 같다.

결정: 직업의 선택. 종속 더미: 감독자 = 감독자일 경우 1개, 감독자가 아닐 경우 0개.

결정: 정당에의 가입. Dependent Dummy: Party에 소속되어 있는 경우 Party = 1, 소속되어 있지 않은 경우 0.

결정: 은퇴 종속 더미: 은퇴한 경우 = 은퇴한 경우 1이고, 은퇴하지 않은 경우 0이다.

질적 의존적 더미 변수가 세 개 이상의 값(많은 정당에 대한 소속 등)을 갖는 경우, 그것은 다당형 또는 다당형 또는 다당형 모델이 된다.^[8]

종속 더미 변수 모델

종속적인 더미 변수 모델의 분석은 다양한 방법을 통해 수행될 수 있다. 그러한 방법 중 하나는 일반적인 OLS 방법인데, 이 맥락에서 선형 확률 모델이라고 한다. 다른 방법은 관측할 수 없는 연속 잠복 변수 Y가^* 있고 관측된 이분법 변수 Y가 0보다^* 크면 1이 된다고 가정하는 것이다. 이것은 로짓과 프로빗 모델의 기본 개념이다. 이 모델들은 아래에 간략히 설명되어 있다.^[9]

선형확률모형

종속 변수 Y가 0과 1의 값을 갖는 이분법적 더미인 일반적인 최소 제곱 모형은 선형 확률 모형(LPM)이다.^[9] 다음 회귀 분석을 고려한다고 가정하자.

${\displaystyle Y_{i}=\alpha _{1}+\alpha _{2}X_{i}+u_{i}}}}}}}$

어디에

${\displaystyle X}$ ${\displaystyle X}$ $$= 가족 소득

${\displaystyle Y}$= ${\displaystyle 1}$ ${\displaystyle Y=1}$ 가족이 집을 소유하고 있는 경우$$, 가족이 집을 소유하고 있지 않은 경우 0

회귀가 선형이기 때문에 이 모형을 선형 확률 모형이라고 한다. $E{\displaystyle \mathbb{}({Yi}_{}}$ ${\displaystyle X{}_{}{}_{}}$ ${\displaystyle i_{}}$) ${\displaystyle \mathb {E}(Y_{i} X_{i$로 기록된 Y_i given X의_i 조건부 평균은 X의_i 해당 값, 즉 Pr(Y_i = 1 X_i)에 대해 사건이 발생할 조건부 확률로 해석된다. 이 예에서 $E{\displaystyle \mathbb{}({Yi}_{}}$ ${\displaystyle X{}_{}{}_{}}$ ${\displaystyle i_{}}$) ${\displaystyle \mathb {E}(Y_{i}X_{i})$는 X가_i 수입을 주는 가족이 집을 소유할 확률을 제공한다$$.

이제 OLS 가정 $E{\displaystyle ({}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle X_{}}$ i${\displaystyle {}_{}}$)${\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle E(u_{i} X_{i}=0}$을$($를) 사용하여 다음과 같은 결과를 얻는다.

${\displaystyle \mathb {E}(Y_{i}X_{i}=\alpha _{1}+\alpha _{2}X_{i}}).$

LPM 모델에는 다음과 같은 몇 가지 문제가 내재되어 있다.

1. 회귀선은 잘 맞는 선이 아니므로 R과² 같은 유의성 측도는 신뢰할 수 없을 것이다.
2. LPM 접근방식을 사용하여 분석되는 모델은 이질적 장애를 갖게 될 것이다.
3. 오차항은 비정규 분포를 가질 것이다.
4. LPM은 종속 변수의 예측 값을 1보다 크거나 0보다 작을 수 있다. 예측 값은 0과 1 사이에 있어야 하는 확률이기 때문에 해석하기 어려울 것이다.
5. LPM 모델의 변수 사이에 비선형 관계가 존재할 수 있으며, 이 경우 선형 회귀 분석은 데이터를 정확하게 적합시키지 못한다.^[4][10]

LPM에 대한 대안

LPM의 한계를 피하기 위해 필요한 것은 설명 변수 X가_i 증가함에 따라 P_i = E(Y_i = 1 X_i)가 0과 1 사이의 범위 내에 있어야 한다는 특징을 가진 모델이다. 따라서 독립변수와 종속변수의 관계는 반드시 비선형이다.

이를 위해 누적분포함수(CDF)를 사용하여 종속적인 더미 변수 회귀 분석을 추정할 수 있다. 그림 4는 랜덤 변수의 CDF와 유사한 'S'자 모양의 곡선을 보여준다. 이 모형에서 확률은 0과 1 사이고 비선형성은 포착되었다. 사용할 CDF의 선택이 이제 의문이다.

로지스틱과 일반 CDF의 두 가지 대체 CDF를 사용할 수 있다. 로지스틱 CDF는 로짓 모델을 만들고 일반 CDF는 프로빗 모델을 만든다.^[4]

로짓 모형

LPM의 단점은 로짓 모델이라 불리는 보다 정교하고 개선된 모델의 개발로 이어졌다. 로짓 모형에서 회귀 방정식의 오차 항의 누적 분포는 로지스틱 분포다.^[9] 회귀는 비선형적이라는 점에서 더 현실적이다.

로짓 모형은 최대우도 접근법을 사용하여 추정한다. 이 모델에서 $P{\displaystyle (Y}$= ${\displaystyle 1}$ ${\displaystyle X}$) ${\displaystyle P(Y=1 X$은 독립 변수가 1인 경우 종속 변수가 1 값을 가질 확률이다.

${\displaystyle P_{i}={\frac {1}{1}{1+e^{-z_{i}}\{\frac {e^{z_{i}}}{1+e^{i}}\}}}}}$

여기서 $z{\displaystyle {}_{}}$ ${\displaystyle i_{}}$= ${\displaystyle {\alpha \mathrm{}}_{}}$ 1${\displaystyle {}_{}}$+ ${\displaystyle {}_{}}$ 2 ${\displaystyle X_{}}$ ${\displaystyle {}_{}{}_{}}$+ ${\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$

그런 다음 모델을 승산비의 형태로 표현한다: 로지스틱 회귀 분석에서 모델링된 것은 오즈의 자연 로그이며, 오즈는 $P{\displaystyle }$/${\displaystyle }$( ${\displaystyle 1}$- ${\displaystyle \mathrm{P}}$) ${\$디스플레이 스타일 $P/(1-P)}$로 정의된다$.$ 오즈의 자연 로그를 취하면 로짓(L_i)은 로지트(L)

${\displaystyle L_{i}=\ln \left({p_{i}}{1-P_{i}}}}\right)=z_{i}=\alpha _{1}+\alpha_{2}X_{i}.}$

이 관계는 L이_i X에_i 대해 선형이라는 것을 보여주지만, 확률은 X에_i 대해 선형적이지 않다.^[10]

프로빗 모델

LPM의 단점을 상쇄하기 위해 개발된 또 다른 모델은 프로빗 모델이다. 프로빗 모델은 로짓 모델과 마찬가지로 비선형성에 대한 접근법을 사용하지만 로지스틱 CDF 대신에 일반 CDF를 사용한다.^[9]

참고 항목

• 이항 회귀 분석
• 차우 테스트
• 가설 검정
• 지시함수
• 선형판별함수
• 다중 공선성

참조

추가 읽기

• Asteriou, Dimitrios; Hall, S. G. (2015). "Dummy Variables". Applied Econometrics (3rd ed.). London: Palgrave Macmillan. pp. 209–230. ISBN 978-1-137-41546-2.
• Kooyman, Marius A. (1976). Dummy Variables in Econometrics. Tilburg: Tilburg University Press. ISBN 90-237-2919-6.

외부 링크

위키다양성은 더미 변수에 대한 학습 자원을 가지고 있다(통계)

• Maathuis, Marloes (2007). "Chapter 7: Dummy variable regression" (PDF). Stat 423: Applied Regression and Analysis of Variance. Archived from the original (PDF) on December 16, 2011.
• Fox, John (2010). "Dummy-Variable Regression" (PDF).
• Baker, Samuel L. (2006). "Dummy Variables" (PDF). Archived from the original (PDF) on March 1, 2006.