공분산 분석

공분산 분석(ANCOVA)은 분산 분석과 회귀 분석을 혼합한 일반 선형 모형입니다.ANCOVA는 종속 변수(DV)의 평균이 종종 처리라고 불리는 범주형 독립 변수(IV)의 여러 수준에서 동일한지 여부를 평가하는 동시에 일차 관심사가 아닌 공변량(CV) 또는 방해 변수라고 알려진 다른 연속 변수의 효과를 통계적으로 제어합니다.수학적으로 ANCOVA는 DV의 분산을 CV에 의해 설명되는 분산, 범주형 IV에 의해 설명되는 분산 및 잔차 분산으로 분해합니다.직관적으로 ANCOVA는 CV의 그룹 수단으로 DV를 '조정'^[1]하는 것으로 간주할 수 있습니다.

ANCOVA 모형은 반응(DV)과 공변량(CV) 사이의 선형 관계를 가정합니다.

${\displaystyle y_{ij}=\mu +\mathrm {B} (x_{ij}-{\overline {x})+\ilon _{ij}.}$

이 방정식에서 DV, ${\displaystyle y_{}}$ i$$(\$displaystyle y_{ij})$는 ih 범주형 그룹 아래의 j번째 관측치이며, CV, ${\displaystyle x_{}}$ i$$(\$display$ style $x_{ij})$는 ih 그룹 아래의 공변량의 j번째 관측치입니다.관측된 데이터에서 파생된 모델의 변수는$$μ {\$displaystyle \mu}($최대 평균) $및{\displaystyle \stackrel{}{}}$ x$$μ {\$displaystyle {x}($$공변량{\displaystyle }$ x$\displaystyle$x}$$의 글로벌 평균)입니다.적합 변수는 ${\displaystyle i_{}}$i \ $displaystyle$\ $tau$_ {$i$ $$} ($IV$의 ih 수준의 효과),$display$ B \ $displaystyle$ B$$（ 라인의 기울기) $및{\displaystyle {}_{}}$ ${\$ ${\displaystyle i_{}}$ j \ $displaystyle$\$epsilon$_ { $ij$} (it 그룹의 j번째 관측치를 나타내는 관련 미검출 오차항)이다.

이 규격에서 범주형 처리 효과는 0$({\displaystyle \underset{i}{\overset{}{}}}$ i ${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle i_{}}$ i $=$)이 된다$.$ \$style \left(\sum$ _${i}^{a}\display _{$i}=$0\$right$).$} 다음과$$ 같이 ^[2]선형 회귀 모형의 표준 가정도 유지된다고 가정한다$.$

사용하다

파워를 높이다

ANCOVA를 사용하면 그룹 내 오차 ^[3]분산을 줄임으로써 통계 검정력을 높일 수 있습니다(그룹 간 유의한 차이가 발견될 확률).이를 이해하려면 그룹 간의 차이를 평가하는 데 사용되는 검정인 F-검정을 이해해야 합니다.F-검정은 그룹 간 설명되는 분산(예: 의료 회복 차이)을 그룹 내 설명되지 않은 분산으로 나누어 계산한다.따라서,

${\displaystyle F=syslogfrac {MS_{between}}{MS_{within}}}}:$

이 값이 임계값보다 크면 그룹 간에 유의한 차이가 있다는 결론을 내립니다.설명되지 않은 분산에는 오차 분산(예: 개별 차이)과 다른 요인의 영향이 포함됩니다.따라서 CV의 영향은 분모로 분류된다.DV에 대한 CV의 효과를 제어할 때 분모에서 CV를 제거하여 F를 크게 함으로써 CV가 존재하는 경우 상당한 효과를 찾을 수 있도록 힘을 증가시킵니다.

기존 차이 조정

ANCOVA의 또 다른 용도는 무가(정밀) 그룹의 기존 차이를 조정하는 것이다.이 논란의 여지가 있는 어플리케이션은 여러 온전한 그룹 간의 DV에 존재하는 초기 그룹 차이(그룹 할당 전)를 수정하는 것을 목적으로 합니다.이 상황에서는 무작위 할당을 통해 참가자를 평등하게 만들 수 없기 때문에 CV가 없는 경우보다 점수를 조정하고 참가자를 더 비슷하게 만드는 데 CV가 사용됩니다.그러나 공변량을 사용하더라도 불평등한 그룹을 동일시할 수 있는 통계 기법은 없습니다.또한 CV는 IV와 매우 밀접하게 관련되어 있기 때문에 CV와 관련된 DV의 분산을 제거하면 DV의 상당한 분산을 제거하여 결과를 ^[4]무의미하게 만들 수 있습니다.

전제 조건

ANCOVA의 기초가 되고 결과의 ^[2]해석에 영향을 미치는 몇 가지 핵심 가정이 있다.표준 선형 회귀 가정은 유지되며, 공변량의 기울기가 모든 처리 그룹(회귀 기울기의 동질성)에서 동일하다고 가정합니다.

가정 1: 회귀의 선형성

종속 변수와 수반 변수 사이의 회귀 관계는 선형이어야 합니다.

가정 2: 오차 분산의 균질성

오차는 서로 다른 처리 클래스 및 관측치에 대한 조건부 0 평균 및 등분산을 갖는 랜덤 변수입니다.

가정 3: 오차항의 독립성

오류는 상관없습니다.즉, 오차 공분산 행렬은 대각 행렬입니다.

가정 4: 오차 항의 정규성

잔차(오류항)는 i$$ \$displaystyle \epsilon$ _${ij}$ ~${\displaystyle }$N (${\displaystyle 0}$ , ${\displaystyle {2\mathrm{}}^{}}$ 2)$${ $displaystyle$N ( $0$, \$sigma ^{2}$)으로 정규 분포를 따라야 합니다.

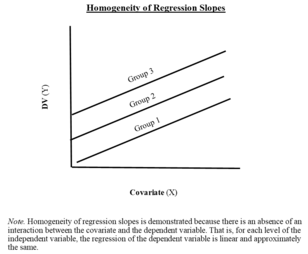
가정 5: 회귀 기울기의 균질성

서로 다른 회귀선의 기울기는 같아야 합니다. 즉, 회귀선은 그룹 간에 평행해야 합니다.

다른 처리 회귀 기울기의 균질성에 관한 다섯 번째 문제는 ANCOVA 모델의 적합성을 평가하는 데 특히 중요하다.또한 오차항만 정규 분포하면 됩니다.사실 대부분의 경우 독립 변수와 부수 변수 모두 정규 분포를 따르지 않습니다.

ANCOVA의 실행

다중 공선성 테스트

CV가 다른 CV와 높은 상관 관계(0.5 이상의 상관 관계)인 경우 DV를 다른 CV보다 높게 조정하지 않습니다.통계적으로 장황하기 때문에 한쪽은 삭제해야 합니다.

분산 가정의 균질성 검정

Levene의 오차 분산 동일성 검정에 의해 검정되었습니다.이것은 조정이 이루어진 후에 가장 중요하지만, 조정 전에 가지고 있는 경우에는 그 후에 가지고 있을 가능성이 높습니다.

회귀 기울기 가정의 균일성 검정

CV가 IV와 유의하게 상호작용하는지 여부를 확인하려면 IV와 CVxIV 상호작용 항을 모두 포함하는 ANCOVA 모델을 실행합니다.CVxIV 상호작용이 중요한 경우 ANCOVA를 수행하지 마십시오.대신, Green & Salkind는^[5] CV의 특정 수준에서 DV의 그룹 차이를 평가할 것을 제안한다.또한 CV와 CV의 교호작용을 다른 IV로 처리하여 감속 회귀 분석을 사용하는 것도 고려해 보십시오.또는 조정 분석을 사용하여 CV가 DV에 미치는 IV의 영향을 설명하는지 여부를 결정할 수 있다.

ANCOVA 분석 실행

CV×가IV 상호 작용은 중요하지 않습니다. CV× 없이 ANCOVA를 다시 실행합니다.IV 상호작용 항.이 분석에서는 수정된 평균과 수정된 MS오차를 사용해야 합니다.조정된 평균(최소 제곱 평균, LS 평균, 추정 한계 평균 또는 EMM이라고도 함)은 DV에 대한 CV의 영향을 제어한 후 그룹 평균을 나타냅니다.

후속 분석

유의한 주효과가 있으면 다른 ^[6]모든 요인을 무시하고 하나의 IV 수준 간에 유의한 차이가 있음을 의미합니다.서로 유의하게 다른 수준을 정확하게 찾으려면 분산 분석과 동일한 추적 검정을 사용할 수 있습니다.IV가 두 개 이상 있으면 유의한 교호작용이 있을 수 있습니다. 즉, DV에 대한 IV의 효과는 다른 요인의 수준에 따라 달라집니다.요인 분산 분석과 동일한 방법을 사용하여 단순 주효과를 조사할 수 있습니다.

전력에 관한 고려 사항

일반적으로 공변량을 분산 분석에 포함하면 종속 변수의 분산 중 일부를 고려하여 통계적 검정력이 증가하므로 독립 변수에 의해 설명되는 분산 비율이 증가하지만 분산 분석에 공변량을 추가하면 자유도도 감소합니다.따라서 종속 변수의 분산을 거의 고려하지 않는 공변량을 추가하면 실제로 검정력이 감소할 수 있습니다.

「 」를 참조해 주세요.

• MANCOVA(다변량 공분산 분석)

레퍼런스

외부 링크

• 랜덤화 블럭, 분할도, 반복 측도, 라틴 제곱 등 처리 요인이 최대 3개인 모든 분산 분석 및 ANCOVA 모형과 R(사우스햄튼 대학)의 분석 예제
• 독립 표본에 대한 일원 공분산 분석
• 공분산 분석은 무엇에 사용됩니까?
• G.J.P. Van Breukelen 및 K.R.A. Van Dik(2007)의 무작위 대조 시험에서 공변량 사용