곤충 비행

곤충은 날개와 비행을 진화시킨 무척추동물의 유일한 집단이다.곤충들은 약 3억 5천만에서 4억년 전에 카본리퍼스에서 처음 날았고, 그들은 비행을 진화한 최초의 동물이 되었다.날개는 이미 다른 용도로 사용되는 신경, 관절, 근육을 가지고 있던 기존 팔다리의 옆구리에 붙이는 것에서 진화했을지도 모른다.이것들은 처음에 물 위를 항해하거나 미끄러질 때 하강 속도를 늦추기 위해 사용되었을 수 있다.

두 곤충 집단인 잠자리들과 잠자리들은 날개에 직접 붙어 있는 비행 근육을 가지고 있다.다른 날개가 달린 곤충들에서는 비행근육이 흉부에 붙어 날개가 뛰도록 유도하기 위해 가슴이 진동하게 만든다.이러한 곤충들 중 일부(파리와 딱정벌레)는 '비동기' 신경계의 진화를 통해 매우 높은 윙비트 주파수를 달성하는데, 이 신경계의 진화는 흉부가 신경 자극 속도보다 더 빠르게 진동하는 것이다.

일부 매우 작은 곤충들은 정상 상태의 공기역학으로 사용하지 않고 Weis-Foh의 박수와 날리기 메커니즘을 사용하여 날개의 마모나 찢어지는 희생을 감수하면서 큰 상승력을 발생시킨다.많은 곤충들이 키를 유지하고 그들의 위치를 조절하면서 맴돌 수 있다.나방과 같은 몇몇 곤충들은 후추와 결합되어 있어서 이러한 곤충들이 한마음으로 작동할 수 있다.

메커니즘

직항편

다른 곤충과는 달리 에페메로프테라(파리지)와 오도나타(잠자리·담자체)의 날개근육은 날개기지에 직접 삽입하는데, 날개기지의 작은 하향운동이 날개 자체를 위로 들어 올리도록 경첩이 달려 있어 마치 공중에서 노를 젓듯이 말이다.잠자리와 잠자리들은 모양과 크기가 비슷한 앞뒤 날개를 가지고 있다.각각은 독립적으로 작동하며, 이것은 다른 날아다니는 곤충에서 볼 수 없는 방향과 속도를 바꿀 수 있는 갑작스러움 측면에서 어느 정도의 미세한 제어와 이동성을 제공한다.오도나이트들은 모두 항공 포식자들로, 그들은 항상 다른 공수 곤충들을 사냥해왔다.^[1]

• 

  직접 비행: 날개에 붙어 있는 근육.큰 곤충만 해당

• 

  오도나타(잠자리, 잠자리)는 파리와 마찬가지로 직접 비행 근육 조직을 가지고 있다.

• 미디어 재생

  잠자리의 느린 움직임 비행

간접비행

직접 비행근육을 가진 두 가지 명령 외에, 다른 모든 살아있는 날개 곤충들은 간접 비행근육을 포함하는 다른 메커니즘을 사용하여 비행한다.이 메커니즘은 한 번 진화했고 인트라클라스 네오프테라의 정의적 특징(시나포모르피)이다; 그것은 아마도 우연히도 아닌 날개 접힘 메커니즘의 출현과 일치한다. 이것은 네오프테란 곤충들이 쉴 때 날개를 복부 위로 다시 접을 수 있게 한다(이 능력은 비록 2차적으로 상실되었지만, 예를 들어, 일부 그룹에서는 두 번째로 상실되었다).안절부절못하여^[1]

그러나 모든 네오프테라가 공유하는 것은 흉곽의 근육이 작용하는 방법이다: 이 근육들은 날개에 붙이기 보다는 흉부에 붙어서 변형시킨다; 날개가 흉부 외골격의 확장이기 때문에 흉곽의 변형 역시 날개가 움직이게 한다.등을 따라 종방향 근육 세트가 흉부를 앞쪽에서 뒤쪽으로 압박해 흉부(공지)의 등측면이 위로 굽혀져 날개가 아래로 뒤집힌다.테르굼에서 흉골에 이르는 또 다른 근육 세트가 노툼을 다시 아래로 잡아당겨 날개가 위로 뒤집히게 한다.^[1][2]

• 

  간접비행: 근육은 대부분의 곤충에서 흉곽을 진동시킨다.

• 

  나비 등 대부분의 곤충을 포함한 네오프테라는 간접 비행 근육 조직을 가지고 있다.

초속 100회 이하로 날개를 치는 곤충은 동기근육을 사용한다.동기근육은 모든 신경충동에 대해 한 번 수축되는 근육의 일종이다.이것은 일반적으로 비동기 근육보다 적은 전력을 생산하고 효율이 낮으며, 이것은 여러 개의 분리된 곤충 군락에서 비동기 비행 근육의 독립적 진화를 설명한다.^[3]

범블비와 같이 날개를 더 빨리 치는 곤충은 비동기 근육을 사용한다; 이것은 신경 충동 당 한 번 이상 수축되는 근육의 일종이다.이것은 근육의 긴장에서의 해소에 의해 근육이 자극을 받아 다시 수축함으로써 이루어지는데, 단순한 신경 자극만으로 이루어지는 것보다 더 빠르게 일어날 수 있다.^[4]이를 통해 날개 박동의 주파수가 신경계가 자극을 보낼 수 있는 속도를 초과할 수 있다.비동기근은 일부 상위 네오프테라(Coleoptera, Diptera, Hymenoptera)에서 나타난 최종 정제 중 하나이다.전체적인 효과는 높은 네오프테라가 직접적인 비행 근육을 가진 곤충보다 훨씬 더 빨리 날개를 칠 수 있다는 것이다.^[1]

공기역학

곤충의 비행에는 두 가지 기본적인 공기역학적 모델이 있다: 선도적인 가장자리 소용돌이를 만드는 것과 박수와 플링의 사용이다.^[5][6]

선행 에지 소용돌이

대부분의 곤충들은 소용돌이치는 가장자리 소용돌이를 만드는 방법을 사용한다.이 펄럭이는 날개는 두 개의 기본적인 반 스트로크를 통해 움직인다.다운 스트로크는 위아래로 그리고 뒤로 시작되어 아래로 그리고 앞으로 곤두박질친다.그러면 날개가 빠르게 뒤집혀(흡수) 앞쪽 가장자리가 뒤로 향하도록 한다.그리고 나서 업 스트로크는 날개를 위아래로 밀어낸다.그러면 다시 날개가 뒤집히고(프론테이션) 또 한 번의 다운 스트로크가 발생할 수 있다.동기식 비행 근육을 가진 곤충의 주파수 범위는 일반적으로 5에서 200 헤르츠(Hz)이다.비동기 비행 근육을 가진 사람들은 날개 비트 주파수가 1000Hz를 초과할 수 있다.곤충이 맴돌 때는 두 획이 같은 시간이 걸린다.그러나 느린 다운 스트로크는 추력을 제공한다.^[5][6]

곤충의 비행을 이해하는 데는 주요 힘의 식별이 중요하다.펄럭이는 날개를 이해하려는 첫 번째 시도는 준안정적인 상태를 가정했다.이것은 어떤 주어진 시간에 날개 위의 공기 흐름은 같은 공격 각도에서 비플래시, 안정 상태 날개 위로 흐르는 흐름과 같다고 가정했다는 것을 의미한다.펄럭이는 날개를 다수의 움직이지 않는 위치로 나눈 다음 각 위치를 분석하면, 매 순간 날개에 가해지는 순간의 힘의 타임라인을 만들 수 있을 것이다.계산된 리프트는 3배수로 너무 작다는 것이 밝혀졌기 때문에 연구자들은 공기역학적 힘을 제공하는 불안정한 현상이 반드시 존재해야 한다는 것을 깨달았다.펄럭이는 날개에 가까운 흐름의 근사치를 시도하는 몇몇 분석 모델들이 개발되고 있었다.일부 연구자들은 힘이 정점에 달할 것이라고 예측했다.동적으로 확장된 초파리의 모델로, 이러한 예측된 힘은 나중에 확인되었다.다른 이들은 복수와 발음을 하는 동안 힘이 정점을 이루는 것은 근본적으로 번역적 현상과 다른 알 수 없는 회전 효과에 의해 발생한다고 주장했다.이 주장에는 약간의 이견이 있다.컴퓨터 유체 역학을 통해 일부 연구자들은 회전 효과가 없다고 주장한다.그들은 높은 힘이 이전 뇌졸중으로 인한 웨이크 헛간과의 상호작용에 의해 발생한다고 주장한다.^[5][6]

위에서 언급한 회전 효과와 유사하게 날개가 펄럭이는 것과 관련된 현상은 완전히 이해되거나 합의되지 않는다.모든 모형은 근사치이기 때문에, 서로 다른 모형은 무시할 수 있는 것으로 추정되는 효과를 배제한다.예를 들어, 허버트 A가 제안한 바그너 효과. 1925년 바그너는 기울어진 날개가 정지 상태에서 가속될 때 점도로 인해 순환이 서서히 안정된 상태로 상승한다고 말한다.^[7]이 현상은 예측한 값보다 적은 리프트 값을 설명할 것이다.일반적으로, 추가 리프트에 대한 공급원을 찾는 것이 사례였다.곤충 비행의 전형인 레이놀즈 숫자를 가진 흐름에는 이 효과가 미미하다는 주장이 제기되어 왔다.레이놀즈 수는 난류의 척도로, 레이놀즈 수가 낮을 때는 층류(스무스름)이고, 높을 때는 난류(스무스)이다.^[8]바그너 효과는 적어도 하나의 모델에서 의식적으로 무시되었다.^[6]곤충이 날아가는 동안 발생하는 가장 중요한 현상 중 하나는 납 가장자리 흡인이다.이 힘은 효율 계산에 중요하다.선행 가장자리 흡착의 개념은 1988년 D. G. 엘리스와 J. L. 스톨리에 의해 첨예한 끝의 델타 날개에 있는 소용돌이의 양력을 묘사하기 위해 처음 제시되었다.^[9]높은 각도의 공격에서는 흐름이 선행 가장자리 위로 분리되지만, 후행 가장자리에 도달하기 전에 다시 부착한다.분리된 흐름의 이 거품 안에는 소용돌이가 있다.공격 각도가 워낙 높기 때문에 많은 추진력이 흐름으로 하향 전달된다.이 두 가지 특징은 많은 양의 리프트 힘뿐만 아니라 약간의 추가적인 드래그도 만들어낸다.그러나 중요한 특징은 리프트다.흐름이 분리되었지만 여전히 많은 양의 양력을 제공하기 때문에, 이 현상을 H에 의해 항공기 프로펠러에서 처음 알려진 스톨 지연이라고 한다.1945년 ^[10]히멜스캄프이러한 효과는 펄럭이는 곤충 비행에서 관찰되었으며 준안정 상태 모델의 결함을 설명하기 위해 충분한 양력을 제공할 수 있는 것으로 입증되었다.이 효과는 카누 선수들이 도태하는 무승부 스트로크에 사용된다.^[5][6]

펄럭이는 날개에 대한 모든 영향은 공기역학 현상의 세 가지 주요 원천으로 축소될 수 있다: 선두 가장자리 소용돌이, 날개의 안정 상태 공기역학적 힘, 그리고 이전 스트로크에서 깨어나 날개가 접촉하는 것이다.날아다니는 곤충의 크기는 약 20마이크로그램에서 약 3그램이다.곤충 체적이 증가하면 날개 면적이 증가하고 날개 박동수가 감소한다.더 큰 곤충의 경우, 레이놀즈 수(Re)는 흐름이 격변하기 시작하는 10000까지 될 수 있다.더 작은 곤충의 경우, 10마리 정도로 낮을 수 있다.이것은 점성 효과가 작은 곤충들에게 훨씬 더 중요하다는 것을 의미한다.^[6][11][12]

다운 스트로크

고공행진행

곤충 비행의 또 다른 흥미로운 특징은 몸의 기울기입니다.비행 속도가 빨라질수록 곤충의 몸은 코 아래로 기울어져 수평이 되는 경향이 있다.이것은 전두부를 감소시키고 따라서 신체 항력을 감소시킨다.항력 또한 전진 속도가 증가함에 따라 증가하기 때문에, 곤충은 이러한 효율이 더욱 필요하게 되면서 비행을 더욱 효율적으로 만들고 있다.또한 다운 스트로크에 대한 공격의 기하학적 각도를 변경함으로써 곤충은 가능한 한 많은 기동을 통해 최적의 효율로 비행을 유지할 수 있다.일반적인 추력의 발달은 리프트 힘에 비해 상대적으로 적다.리프트 힘은 곤충의 무게의 3배 이상일 수 있고, 최고 속도의 추진력은 무게의 20%까지 낮을 수 있다.이 힘은 주로 펄럭이는 동작의 힘이 덜한 업 스트로크를 통해 개발된다.^[6][13]

박수를 치고 던지다

덴마크 동물학자 토르켈 웨이스포그가 발견한 박수와 날림, 또는 위스포그 메커니즘은 작은 곤충 비행 중에 이용하는 리프트 생성 방법이다.^[14]곤충의 크기가 1mm 미만이 되면 점성력이 우세해지고 에어포일로부터의 리프트 생성효율이 급격히 감소한다.박수를 치는 자세에서 시작하여 두 날개가 휙 날아가 후행 가장자리를 중심으로 회전한다.그리고 나서 날개는 분리되어 다운 스트로크가 끝날 때까지 수평으로 쓸린다.다음으로, 날개는 고공 줄타기 동작 중에 앞쪽 가장자리를 발음하고 활용한다.박수 동작이 시작되면 선두 가장자리가 만나 갭이 사라질 때까지 함께 회전한다.처음에는 날개가 닿는다고 생각했지만, 몇몇 사건들은 날개의 간극을 나타내며 공기역학적 이점을 제공한다는 것을 암시한다.^[15][16]

클랩과 플링 메커니즘으로부터의 리프트 생성은 모션 전체에 걸쳐 여러 프로세스 중에 발생한다.첫째로, 이 메커니즘은 날개-날개 상호작용에 의존하는데, 이는 단일 날개 운동이 충분한 양력을 만들어내지 못하기 때문이다.^[17][18][19]날개가 튕기는 동작에서 후행 가장자리를 중심으로 회전할 때, 공기는 생성된 틈새로 돌진하여 강한 선행 가장자리 소용돌이를 생성하며, 두 번째 가장자리는 윙팁에서 발달한다.세번째, 약한 소용돌이는 후행 가장자리에서 발생한다.^[16]개발 중인 vortices의 강도는 플링 모션 시작 시 날개 간 분리의 초기 간격에 부분 내 의존한다.날개 사이의 간격이 감소하면 더 큰 드래그 힘의 비용으로 더 큰 리프트 발생을 나타낸다.플라이 중 무게중 운동,^[20] 유연한 날개,^[18] 지연된 스톨 메커니즘의 구현은 소용돌이 안정성과 부착력을 강화하는 것으로 밝혀졌다.^[21]마지막으로, 낮은 레이놀즈 수 비행 중 전체적인 낮은 리프트 생산량을 보상하기 위해( 층류 흐름으로), 작은 곤충들은 종종 더 큰 곤충에 필적하는 날개 끝 속도를 생성하기 위해 더 높은 스트로크 빈도를 가진다.^[21]

날개가 분리되고 회전해야 하기 때문에 등날개 플링 동작 중에 예상되는 전체 최대 드래그 힘이 발생한다.^[19]큰 드래그 힘의 감쇠는 몇 가지 메커니즘을 통해 발생한다.플렉시블 날개는 날갯짓 동작의 드래그를 최대 50%까지 줄이고, 단단한 날개에 비해 날개 스트로크 전체를 통한 전체적인 드래그를 더욱 줄이는 것으로 나타났다.^[18]Encarsia formosa에서 볼 수 있듯이 날개 가장자리에 있는 칫솔은 낮은 리프트 생성 비용으로 드래그력을 증가시키고 감소시키는 흐름의 다공성을 유발한다.^[22]또한, 던지기 전의 윙 간 분리는 드래그의 전체적인 효과에 중요한 역할을 한다.날개 사이의 거리가 늘어나면 전체적인 드래그도 줄어든다.^[15]

박수와 날림 메커니즘은 바다나비인 해양 연체동물 리마시나 헬리키나에도 사용된다.^[23][24]식물 잎 채굴자인 리리오미자 사티바에(파리)와 같은 일부 곤충은 부분적인 박수와 휙휙 날아다니며 날개의 바깥쪽에만 있는 메커니즘을 이용하여 맴돌 때 약 7%의 양력을 증가시킨다.^[21]

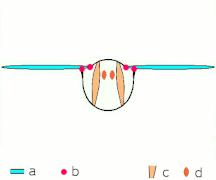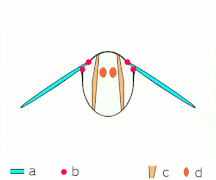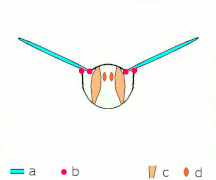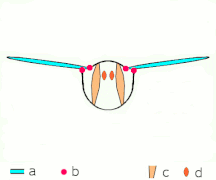
• Sane 2003 이후 박수와 플리핑 비행 메커니즘
• 

  박수 1: 날개가 뒤로 바짝 붙는다.

• 

  클랩 2: 선행 에지 터치, 윙이 선행 에지를 중심으로 회전, 포티스가 형성됨

• 

  박수 3: 후행 가장자리 닫기, 격자 빠짐, 날개 닫힘으로 추력 부여

• 검은색(커브) 화살표: 흐름, 파란색 화살표: 유도 속도, 주황색 화살표: 날개 위의 순 힘
• 

  플립 1: 날개가 후행 가장자리를 중심으로 회전하여 흩어짐

• 

  플립 2: 앞쪽 가장자리가 멀리 이동, 공기가 밀려들어 상승

• 

  플립 3: 선행 에지에서 새로운 소용돌이가 형성되고, 후행 에지 포트리스가 서로를 취소하며, 아마도 흐름이 더 빠르게 성장하는 데 도움이 될 것이다(Weis-Foh 1973).

지배 방정식

유체에서 움직이는 날개는 유체의 힘을 경험하는데, 이것은 공기역학에서 발견되는 규약을 따른다.날개에 상대적인 흐름 방향에 정상적인 힘 성분을 리프트(L)라고 하며, 흐름의 반대 방향에 있는 힘 성분을 드래그(D)라고 한다.여기서 고려한 레이놀즈 번호에서 적절한 힘 단위는 1/2(()이며², 여기서 ρ은 유체의 밀도, S는 날개 면적, U는 날개 속도다.치수가 없는 힘을 리프트(C_L)와 드래그(C_D) 계수라고 하는데,^[5] 이는 다음과 같다.

${\displaystyle C_{\text{L}}(\alpha )={\frac {2L}{\rho U^{2}S}\quad {\text{and}}\qad C_{\d}(\alpha )={\frac {2D}{\rho U^{2}S}}.}$

C와_L C는_D 흐름이 일정할 때만 상수다.에어포일과 같은 특별한 등급의 물체는 작은 공격 각도로 유체를 잘라서 통과할 때 안정된 상태에 도달할 수 있다.이 경우 에어포일 주위의 비침습 흐름은 비침투 경계 조건을 만족하는 전위 흐름에 의해 근사치를 구할 수 있다.2D 에어포일의 Kutta-Joukowski 정리는 추가로 흐름이 날카로운 후미 가장자리를 부드럽게 떠난다고 가정하고, 이것이 에어포일 주위의 총 순환을 결정한다.상응하는 양력은 베르누이의 원리(블라시우스 정리)에 의해 주어진다.^[5]

${\displaystyle C_{\text{L}}=2\pi \sin \alpha \quad {\text{and}}\quad C_{\text{\text}D}=0.}$

새와 곤충 주위의 흐름은 압축할 수 없는 것으로 간주될 수 있다.마하 수, 즉 공기의 소리 속도에 상대적인 속도는 일반적으로 1/300이며 날개 주파수는 약 10–103 Hz이다.Navier-Stokes 방정식을 Navier-Stok크스 방정식으로 사용하여 미끄럼 방지 경계 조건의 적용을 받는 등식은 다음과 같다.^[5]

${\displaystyle {\begin{aligned}{\frac {\partial \mathbf {u} }{\partial t}}+\left(\mathbf {u} \cdot \nabla \right)\mathbf {u} &=-{\frac {\nabla p}{\rho }}+v\nabla ^{2}\mathbf {u} \\\nabla \cdot \mathbf {u} &=0\\\mathbf {u} _{\text{bd}}&=\mathbf {u} _{\text{s}}.\end{정렬}}}$

여기서 u(x, t)는 유량장, p 압력, ρ 유체의 밀도, ν 키네마틱 점도, u_bd 경계에서의 속도, u_s 고체의 속도.길이 척도 L, 속도 척도 U를 선택하면 레이놀즈 번호 R_e=uL/males를 포함하는 비차원적 형태로 방정식을 표현할 수 있다. 곤충 날개와 공기포일 사이에는 두 가지 분명한 차이가 있다.곤충의 날개는 훨씬 작아서 펄럭인다.잠자리의 화음(c)은 1cm(0.39인치), 날개 길이(l)는 약 4cm(1.6인치), 날개 주파수(f)는 약 40Hz이다.팁 속도(u)는 약 1m/s(3.3ft/s)이며, 해당 레이놀즈 번호는 약 103이다.작은 끝에서 일반적인 찰시도이드 와스프는 날개 길이가 약 0.5–0.7 mm(0.020–0.028 in)이고 날개를 약 400 Hz로 박동한다.그것의 레이놀즈 수는 약 25개 입니다.곤충 비행에서 레이놀즈 수의 범위는 약 10~10개로⁴, 이론에 편리한 두 가지 한계 사이에 있다: 에어포일 주위로 무분별한 꾸준한 흐름과 수영 박테리아가 경험하는 스톡스 흐름이다.이 때문에 이 중간 범위는 잘 파악되지 않는다.반면에, 그것은 아마도 우리가 보는 것들 중에서 가장 보편적인 정권일 것이다.떨어지는 나뭇잎과 씨앗, 물고기, 새들은 모두 곤충 주변에서 볼 수 있는 것과 비슷한 불안정한 흐름을 만난다.^[5]현악 레이놀즈 번호는 다음과 같이 설명할 수 있다.

${\displaystyle Re={\frac {{\bar{c}}U}{v}}}$

${\displaystyle U}$= ${\displaystyle 2}$ ${\displaystyle \mathrm{\theta }}$ f ${\displaystyle g_{}}$ ${\$${\displaystyle \sqrt{g}}$$}$ 및 $r$ g =${\displaystyle {}_{}{1}_{}}$ ${\displaystyle s\sqrt{\frac{\mathrm{}}{}}}$ ${\displaystyle \sqrt{\frac{s}{}{}_{}^{}}}$0 ${\displaystyle \sqrt{{R\mathrm{}}_{}^{}}}$ ${\displaystyle \sqrt{{}_{}^{}{}^{}}}$ ${\displaystyle \sqrt{{}^{}}}$ ${\displaystyle \sqrt{c}}$(${\displaystyle \sqrt{}}$R ) ${\displaystyle \sqrt{d}}${\$displaysty r_{g}={\qrt {{\frac{1}}}}\int$_{$0}^{r^{r}{{2}c(R)}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

여기서 $c$의${\displaystyle \stackrel{}{}}$${\$$displaystyle {\bar$ {c$}\}\}$은(는) 평균 $화음{\displaystyle }$ 길이$,$ U {\$displaystyle$ U}은$($는) 날개 $팁$의 속도$,$ $display$ {\$displaystyle$ $\Theta}$은(는) $스트로크{\displaystyle }$ 진폭,$$f {\$displaystyth$ f$}$은 비트 주파수, $r_{g}$은 교정의$$반지름 s$}$이다.e 윙 영역 및 $R{\displaystyle }$ ${\displaystyle R}$은(는) 윙 팁을 포함한 윙의 길이입니다$$.

레이놀즈 번호 외에도 적어도 두 개의 관련 없는 차원이 없는 매개변수가 있다.날개에는 몸체에 대한 펄럭이는 속도(u), 몸체의 전진 속도(U₀), 투구 속도(Ωc)의 세 가지 속도 눈금이 있다.그 비율은 U₀/u와 Ωc/u라는 두 가지 차원이 없는 변수를 형성하는데, 전자를 흔히 전진비라고 하며, 감소된 주파수인 fc/U와도₀ 관련이 있다.^[5]

예를 들어 곤충 날개가 경직된 경우, 예를 들어, 드로필라 날개가 대략 그렇다면, 고정된 몸체에 대한 그것의 움직임은 세 가지 변수로 설명될 수 있다: 구면 좌표에서 팁의 위치, θ(t), φ(t), 투구 각도 ψ(t)이다.블레이드 요소 분석을 기반으로 공기역학적 힘을 추정하려면 공격 각도(α)도 결정해야 한다.윙스팬 70%에서 일반적인 공격 각도는 맴도는 곤충에서 25°~45°(벌새에서는 15°)이다.많은 곤충들이 이용할 수 있는 풍부한 데이터에도 불구하고 뇌졸중 동안 α의 시간 변동을 보고하는 실험은 비교적 드물다.그 중에는 메뚜기떼와 파리떼의 풍동실험, 초파리떼의 자유항행 등이 있다.^[5]

상대적으로 측정이 용이하기 때문에 날개끝 궤적이 더 자주 보고되고 있다.예를 들어, 무게를 지탱하기에 충분한 양력을 생성하는 비행 순서만 선택하면 날개 끝이 타원형 모양을 따른다는 것을 알 수 있다.다른 곤충들에게도 비크로싱 모양들이 보고되었다.정확한 모양과 상관없이, 플러그-다운 운동은 곤충들이 무게를 지탱하기 위해 들어올리는 것 외에도 공기역학적 드래그를 사용할 수 있다는 것을 나타낸다.^[5]

맴버링

비행 매개변수[25]	속도(m/s)	비트/초
애쉬니드잠자리	7.0	38
호넷	5.7	100
벌새 산호초	5.0	85
말파리	3.9	96
호버플라이	3.5	120
범블비	2.9	130
꿀벌	2.5	250
집파리	2.0	190
담셀프ly	1.5	16
스콜피온플라이	0.49	28
큰흰나비[26]	2.5	12
절약(딱딱딱딱딱딱)[21]	0.3	254

많은 곤충들은 날개를 빠르게 치면서 공중의 한 지점에서 맴돌거나 머무를 수 있다.그렇게 하려면 양력 생산뿐만 아니라 측면 안정화가 필요하다.인양력은 주로 다운 스트로크로 발생한다.날개가 주위의 공기를 밀어내자, 그 결과 날개의 공기의 반응력이 곤충을 밀어올린다.대부분의 곤충의 날개는 상향 획을 치는 동안 날개에 가해지는 힘이 작도록 진화한다.다운비트와 리턴 스트로크는 각각 곤충을 위아래로 움직이게 하기 때문에 곤충은 진동하고 같은 위치에 있게 된다.^[11]

곤충이 날개짓 사이에서 떨어지는 거리는 날개짓 속도가 얼마나 빠른가에 따라 달라지는데, 날개짓이 느릴수록 떨어지는 간격은 길어지고 날개짓 사이는 멀어지는 것이다.곤충이 진폭에서 일정한 안정성을 유지하는 데 필요한 윙비트 주파수를 계산할 수 있다.계산을 단순화하려면 날개가 아래로 움직이는 동안 리프팅 힘이 유한 상수 값에 있고 날개가 위로 움직이는 동안 0이라고 가정해야 한다.위 윙비트의 시간 간격 Δt 동안 곤충은 중력의 영향을 받아 거리를 h로 떨어뜨린다.^[11]

${\displaystyle h={\frac {g(\Delta t^{2})}{2}}}$

그 후 위로 올리면 곤충이 원래 위치로 회복된다.일반적으로 곤충의 수직 위치가 0.1 mm(즉, h = 0.1 mm) 이하로 변경되어야 할 수 있다.자유낙하의 최대 허용시간은 다음과 같다.

${\displaystyle \Delta t=\left({\frac {2h}{g}}\right)^{1/2}={\sqrt {\frac {2\times 10^{-2}{\text{ cm}}}{980{\text{ cm}}/{\text{s}}^{2}}}}\approx 4.5\times 10^{-3}{\text{ s}}}$

날개의 상승운동과 하강운동은 지속시간상 거의 같기 때문에 완전한 상하의 날개에 대한 주기 T는 2배 Δr, 즉,^[11]

${\displaystyle T=2\,\Delta t=9\time 10^{-3}{\text{s}}}$

초당 날개짓의 수를 의미하는 박자의 주파수 f는 다음과 같은 방정식으로 표현된다.^[11]

${\displaystyle f={\frac {1}{T}}\약 110{\text{s}^{-1}$

사용된 예에서 사용되는 주파수는 곤충에서 발견되는 전형적인 주파수인 110박자/s이다.나비는 약 10박자/s로 훨씬 느린 주파수를 가지고 있는데, 이것은 그들이 맴돌 수 없다는 것을 의미한다.다른 곤충들은 1000박자/s의 주파수를 생산할 수 있을 것이다.곤충을 원래 수직 위치로 복원하기 위해서는 하향 행정 중 평균 상승력인 F가_av 곤충의 무게의 2배와 같아야 한다.참고로 곤충 몸에 가해지는 상승력은 절반만 적용되기 때문에 곤충에 가해지는 평균 상승력은 단순히 무게에 불과하다는 점에 유의한다.^[11]

전력입력

이제 질량 m 0.1g의 곤충을 다시 한 번 생각해 보면, 아래 스트로크 중 양 날개에 의해 적용되는 평균 힘 F는_av 무게의 2배라는 것을 생각할 때, 주위를 맴도는 데 필요한 힘을 계산할 수 있다.날개에 의해 가해지는 압력이 전체 날개 영역에 균일하게 분포하기 때문에, 각 날개에 의해 발생하는 힘이 날개 중간 부분의 단일 지점을 통해 작용한다고 가정할 수 있다.아래로 내려가는 동안 날개의 중심은 수직 거리를 가로지른다 d.^[11]각 하향 행정 동안 곤충에 의해 수행되는 총 작업은 힘과 거리의 산물이다. 즉,

${\displaystyle {\text{작업}}=F_{av}\time d={\text{2번W}_{\text{d}\,\!}$

만약 날개가 70° 각도로 비트를 통과하여 휘둘러진다면, 1 cm 길이의 날개로 곤충을 위해 제시된 경우 d는 0.57 cm이다.따라서 양 날개에 의한 각 획에 행해지는 일은 다음과 같다.^[11]

${\displaystyle {\text{작업}}=2\time 0.1\time 980\time 0.57=112{\text{erg}\,\!}$

그 에너지는 중력에 대항하여 곤충을 기르는데 사용된다.다운 스트로크 시 곤충의 질량을 0.1 mm 상승시키는 데 필요한 에너지 E는 다음과 같다.^[11]

${\displaystyle {\text{E}}={\text{mgh}=0.1\cHB 980\cHB 10^{-2}=0.98{\text{erg}\,\!}$

이것은 분명히 대부분의 에너지가 다른 과정에서 소비되는 총 에너지 중 무시할 수 있는 부분이다.문제의 보다 자세한 분석은 날개에 의해 행해지는 작업이 주로 날개의 하향 획에 의해 가속되는 공기의 운동 에너지로 전환된다는 것을 보여준다.그 힘은 1초 동안 행해지는 일의 양이다. 예를 들어 곤충의 경우 초당 110타를 내리친다.따라서 전력 출력 P는 초당 스트로크이며, 이는 전력 출력 P가 다음과 같음을 의미한다.^[11]

${\displaystyle {\text{P}}=112{\text{erg}\time 110{\text{/s}=1.23\time 10^{4}{\text{erg/s}{1.23\time 10^{-3}{\text}{\text{\text}}}W}}$

출력

맴돌 때 사용되는 힘의 계산에서 사용된 예는 움직이는 날개의 운동 에너지를 무시했다.곤충의 날개는, 있는 그대로의 빛은 유한한 질량을 가지고 있다. 따라서, 곤충들이 움직일 때, 그들은 운동에너지를 가지고 있다.날개가 회전 운동이기 때문에 각 날개 스트로크 동안 최대 운동 에너지는 다음과 같다.^[11]

${\displaystyle KE={\frac {1}{2}}I\omega _{\text{max}^{2}}$

여기서 I는 날개의 관성 모멘트로, Ω은_max 날개의 스트로크 중 최대 각도 속도다.날개에 대한 관성 모멘트를 얻기 위해 한쪽 끝에서 회전하는 얇은 막대에 의해 날개가 근사치를 얻을 수 있다고 가정할 것이다.날개의 관성 모멘트는 다음과 같다.^[11]

${\displaystyle I={\frac {m\ell ^{2}}{3}}}$

여기서 l는 날개 길이(1 cm)이고 m은 두 날개의 질량이며, 일반적으로 10⁻³ g일 수 있다.최대 각도 속도 Ω은_max 날개 중심에서 최대 선형 속도 ,에서_max 계산할 수 있다.^[11]

${\displaystyle \omega_{\text{max}={\frac {v_{\text{max}}{\ell /2}}:}$

각 스트로크 동안 날개 중심은 날개 중심에서 가로지르는 거리로 주어진 평균 선형 속도 ν으로 이동한다_av.앞의 예에서 d = 0.57 cm, Δt = 4.5×10⁻³ s.따라서 다음과 같다.^[11]

${\displaystyle v_{av}={\frac {d}{\Delta t}={\frac {0.57}{4.5\cHB 10^{-3}}={\text{cm/s}}}$

날개 속도는 날개 획의 시작과 끝에서 모두 0으로, 최대 선형 속도가 평균 속도보다 높다는 것을 의미한다.만약 속도가 날개 경로를 따라 진동한다고 가정한다면, 최대 속도는 평균 속도보다 2배 더 높다.따라서 최대 각도 속도는 다음과 같다.^[11]

${\displaystyle \omega_{\text{max}={\frac {254}{\ell /2}}:}$

따라서 운동 에너지는 다음과 같다.^[11]

${\displaystyle KE={\frac {1}{2}}I\omega _{max}^{2}=\left(10^{-3}{\frac {\el}}}{3}\right)\left({\frac {254}{\ell /2}}\right)^{2}=43{\text{er}}}}}}}}}}}$

날개 움직임의 각 사이클에는 두 개의 날개 획(고공과 다운 스트로크)이 있기 때문에 운동 에너지는 2×43 = 86 에르그다.이것은 그자체를 맴돌 때 소비되는 에너지만큼 크다.^[11]

탄력성

곤충들은 날개가 가속할 때 근육에 의해 제공되는 운동에너지를 얻는다.날개가 스트로크의 끝을 향해 감속하기 시작할 때, 이 에너지는 반드시 소멸해야 한다.다운 스트로크 동안 운동 에너지는 근육 자체에 의해 소멸되어 열로 전환된다(이 열은 때때로 코어 체온을 유지하기 위해 사용된다).어떤 곤충들은 날개의 상승 운동에서 운동 에너지를 이용하여 그들의 비행을 도울 수 있다.이 곤충들의 날개관절에는 레실린이라고 불리는 탄력 있고 고무와 같은 단백질의 패드가 들어 있다.날개의 고공행진 중에는 리실린이 늘어나게 된다.날개의 운동 에너지는 팽창된 레실린에서 전위 에너지로 변환되어 에너지를 샘처럼 많이 저장한다.날개가 아래로 움직이면 이 에너지가 방출되고 다운 스트로크를 돕는다.^[11]

몇 가지 간단한 가정을 통해 우리는 늘어난 레실린에 저장된 에너지의 양을 계산할 수 있다.비록 레실린이 복잡한 모양으로 구부러지지만, 주어진 예는 면적 A와 길이의 직선봉으로 계산한 것을 보여준다.게다가, 우리는 그 스트레칭 내내 레실린이 Hoke의 법칙에 복종한다고 가정할 것이다.이는 레실린이 상당량 늘어나므로 스트레칭 과정에서 부위와 영의 계수가 모두 달라지기 때문에 엄밀히 말해 사실이 아니다.늘어난 레실린에 저장된 잠재적 에너지 U는 다음과 같다.^[11]

${\displaystyle U={\frac {1}{1}:{2}}: {EA\Delta \ell ^{2}}:{\ell}}}$

여기 E는 1.8×10⁷ dyn/cm로² 측정된 리실린에 대한 영의 계량이다.일반적으로 벌 크기의 곤충에서 레실린의 부피는 길이 2×10cm⁻², 면적 4×10cm의⁻⁴² 실린더와 같을 수 있다.주어진 예에서, 리사이신 막대의 길이는 늘어나면 50% 증가한다.즉 Δδ은 10⁻² cm이다.따라서 이 경우 각 날개의 레실린에 저장된 잠재적 에너지는 다음과 같다.^[11]

${\displaystyle U={\frac {1}{1}:{2}}: {\frac {1}.8\cHB 10^{7}\cHB 10^{-4}\cHB 10^{-4}}{2\cHB 10^{-2}}=18\{\text{erg}}}}}}$

벌 크기의 곤충을 위해 두 날개에 저장된 에너지는 36에르그로 날개의 고공행진에서 운동 에너지에 버금간다.실험 결과 날개 운동 에너지의 80%가 레실린에 저장될 수 있다.^[11]

윙 커플링

레피도프테라와 같은 일부 네 개의 날개 곤충 주문은 이미지의 형태학적 날개 연결 메커니즘을 개발하여 이러한 곤충을 기능적으로 두 개의 날개로 만들었다.^[27]가장 기초적인 형태를 제외한 모든 형태는 이 날개 결합을 보여준다.^[28]

이 메커니즘은 세 가지 유형으로 구성되어 있다. - jugal, frenulo-retinural 및 amplexiform:^[29]

• 보다 원시적인 집단은 기저 후미진 부근에 확대된 로브 같은 부위가 있는데, 즉 비행 중 후미진 아래 접히는 전방의 밑부분, 주검이 있다.^[28][30]
• 다른 그룹들은 전방의 레티나쿨럼 아래 갈고리를 채우는 후미에는 소대가 있다.^[30]
• 거의 모든 나비들과 봄비코이데아(스핑과 제외)에서는 날개를 결합시키기 위한 소란과 레티나쿨룸의 배열이 없다.대신, 후방의 확대된 인적 영역이 전방에 의해 크게 중첩된다.특정한 기계적 연결이 없음에도 불구하고 날개는 겹쳐서 단계별로 작동한다.전위의 파워 스트로크가 일제히 후진을 내리누른다.이런 종류의 결합은 광둥형의 변형이지만, 소낭과 망막은 완전히 상실된다.^[27][31]

생화학

곤충 비행의 생화학은 상당한 연구의 초점이 되어 왔다.많은 곤충들이 탄수화물과 지질을 비행의 에너지원으로 사용하는 반면, 많은 딱정벌레와 파리들은 아미노산 프로라인을 그들의 에너지원으로 사용한다.^[32]만두카 섹스타와 같은 일부 종들은 또한 탄수화물을 비행 전 준비운동을 위해 사용한다.^[33]

감각 피드백

곤충들은 비행을 유지하고 통제하기 위해 감각적 피드백을 사용한다.연구는 비행 자세, 날개 비트 진폭, 날개 비트 주파수를 조절하는 데 더듬이,^[34] 할티^[35], 날개와^[36] 같은 감각 구조의 역할을 입증했다.

진화 및 적응

3억 5천만에서 4억년 전, 약 3억 5천만 년 전, 주요 땅덩어리가 두 개 밖에 없었던 시기에 곤충들이 날기 시작했다.^[37]가장 오래된 날개가 달린 곤충 화석들 중에는 Delitzschala가 있다. Delitschala는 Lower Carbinipherous의 Palaeodictyopteran;^[38] Rhyniogatha는 Early Devonian에서 온 더 나이가 많지만, 그것이 날개를 가지고 있었는지, 아니면 실제로 곤충이었는지는 불확실하다.^[39][40]

곤충의 날개가 어떻게 그리고 왜 발달했는지는 잘 이해되지 않는데, 주로 저탄소성분에서 발달한 시기부터 적절한 화석이 부족하기 때문이다.곤충 비행의 기원에 대해서는 역사적으로 크게 세 가지 이론이 있었다.첫 번째 것은 그들이 잠자리 수생 나이아드에서 발견된 가동성 복부 아가미의 변형이라는 것이다.기질 분석은 메뚜기를 포함하는 날개 곤충의 집단인 폴리네오프테라가 육지 조상으로부터 진화하여 아가미에서 날개의 진화는 불가능하다는 것을 시사한다.^[41]파리 유충의 점핑거동에 대한 추가 연구는 기관 아가미가 곤충의 하강을 안내하는 데 아무런 역할을 하지 않는다는 것을 밝혀냈으며, 이 진화 가설에 대한 추가적인 증거를 제공했다.^[42]이것은 두 가지 주요한 역사적 이론을 남긴다: 날개는 편집성 로브, 흉부 테르가의 확장으로부터 발달했다; 혹은 그것들은 이미 근육을 포함하고 있는 다리 부분의 변형에서 생겨났다.^[43]

상피(악 가설

1871년 랜두아, 1873년 러벅, 1877년 그래버, 1905년 오스본 등 수많은^[44] 곤충학자들이 곤충 날개의 가능한 기원은 파리의 나이아드와 같은 많은 수생 곤충에서 발견되는 이동 가능한 복부 아가미일 수도 있다고 제안했다.이 이론에 따르면 호흡기의 출구로 시작되어 시간이 지나면서 기관차 용도로 변형된 이 기관차 아가미는 결국 날개로 발전했다.기관지 아가미는 끊임없이 진동하는 작은 날개와 그들만의 작고 곧은 근육을 가지고 있다.^[45]

편집성 가설

others,[48]의paranotal 돌출부 또는 등 의(등 신체 벽)가설, 프리츠 뮐러에 의해 1875[46]에 및 GCrampton에 의해 1916,[44]Jarmila Kulakova-Peck에 1978[47]에 짓는 청혼을 했고 알렉산더 P.Rasnitsyn은 1981년은 곤충의 날개는paranotal 위에서, 전 적응은 assi을 것이다 곤충 화석에서 발견된 것을 시사한다.sted stabilizati깡충깡충 뛰거나 넘어지면서이 가설에 찬성하는 것은 대부분의 곤충들이 나뭇가지에 올라가다가 깜짝 놀랄 때 땅으로 떨어져서 탈출하려는 경향이다.그러한 로브는 낙하산 역할을 했을 것이고 곤충이 더 부드럽게 착륙할 수 있게 했을 것이다.이 이론은 이 로브들이 점차적으로 더 커졌고 후에 흉부와의 관절을 발달시켰다는 것을 암시한다.심지어 나중에라도 이 조잡한 날개를 움직일 근육들이 나타나곤 했다.이 모델은 낙하산으로 시작해서 활공, 그리고 마지막으로 활공 비행을 시작하는 날개의 효과의 점진적인 증가를 의미한다.그럼에도 날개 관절과 근육의 발달에 대한 실질적인 화석 증거의 부족은 겉으로 보기에 자발적인 관절과 정맥의 발달이 그렇듯이 이론에 큰 난관을 일으키며, 그 분야의 전문가들에 의해 크게 거부되어 왔다.^[45]

엔드라이트-엑시트(쾌락) 가설

1990년, J. W. H. 트루먼은 날개가 종말과 외측에서 변형된 것으로서 흉막 가설이라고도 불리는 원시 절지동물 사지의 각각의 내측과 외측 측면에 추가될 것을 제안했다.이는 1945년 골드슈미트가 드로소필라 멜라노가스터에 대한 연구를 바탕으로 한 것으로, '팟'(포도메레스의 경우, 사지 분절)이라고 불리는 변이가 정상적인 날개를 변형시키는 돌연변이를 보였다.그 결과는 일부 추가 부속이 있는 트리플 이음새 다리 배열로 해석되었지만 날개의 비용적인 표면이 정상적으로 있을 타르수스가 결여되어 있었다.이 돌연변이는 다리가 아닌 등사성 엑사이트와 엔드라이트 융합에 대한 강력한 증거로 재해석되었으며, 이 가설과 함께 부록이 훨씬 잘 어울린다.날개의 진화에 필요한 내경, 관절, 근골은 이미 사지 부분에 존재한다.^[43]

기타 가설

다른 가설들은 빈센트 위글스워스가 1973년에 제안한 흉부 돌출부로부터 날개가 방사기로 사용되었다는 것을 포함한다.^[45]

아드리안 토마스와 노버그는 2003년에 몇몇 돌파리에서 볼 수 있는 것처럼 수면 위를 항해하기 위해 날개가 처음에 진화했을 수도 있다고 제안했다.^[49][50]

스티븐 P.야노비악과 동료들은 2009년 날개가 공중 활공 강하로 인해 날개가 날아온다고 제안했다. 이는 날개가 없는 곤충의 자매 세손인 일부에서 발견되는 비행 전 현상이다.^[51]

이중원점

아에노프,^[52][53] 니와, 엘리아스네토와^[54] 그들의 동료들을 포함한 생물학자들은 곤충의 날개의 기원을 궁전학적 증거 외에도 evo-devo를 사용하여 탐구하기 시작했다.이것은 날개가 테갈과 늑골 구조와 연속적으로 동음이의어라는 것을 암시하며, 수세기 동안 지속되어온 논쟁을 잠재적으로 해결할 수 있다.^[55]Jakub Prokop과 동료들은 2017년 고생대 님팔 날개 패드에서 날개가 실제로 그러한 이중적 기원을 가지고 있다는 팔래온학 증거를 발견했다.^[56]

참고 항목

• 조류 비행
• 날고 미끄러지는 동물
• 글라이딩 개미
• 곤충 이동
• 무인항공기

참조

읽고 추가

외부 링크

위키미디어 커먼즈에는 곤충 비행과 관련된 미디어가 있다.

• 소형항공기 개발에 있어서 곤충의 역할
• 곤충처럼 펄럭이는 초소형 공기차량
• 곤충 비행의 새로운 공기역학: 마이크로 에어 차량에 응용
• 곤충 비행의 공기역학
• 비행근육
• 나비 공기역학적 메커니즘의 흐름 시각화
• 범블비의 비행
• 곤충 비행