인비스시드 흐름

비실비실 유체는 비실비실 유체의 흐름으로, 유체의 점도가 0과 같다.^[1] 슈퍼플루이드라고 알려진 비피시드 액체의 예는 한정되어 있지만, 비피시드 흐름은 유체 역학에서 많은 응용을 한다.^[1][2] 레이놀즈 비점성 흐름의 수는 점도가 0에 가까워질 때 무한에 접근한다.^[1] 비점성 흐름의 경우처럼 비점성 힘이 방치될 경우, Navier–스토크 방정식은 오일러 방정식으로 알려진 형태로 단순화할 수 있다.^[1] 이 단순화된 방정식은 점도가 낮고 레이놀즈 수가 1보다 훨씬 큰 흐름뿐만 아니라 비점성 흐름에도 적용된다.^[1] 오일러 방정식을 사용하면 낮은 점도와 관련된 많은 유체 역학 문제를 쉽게 해결할 수 있지만, 무시할 수 있는 점도는 고체 경계 근처의 유체 영역에서 더 이상 유효하지 않다.^[1][3][4]

액체 자체는 불규칙한 흐름이 일어나기 위해 점성이 0일 필요는 없다. 점성력이 사라지도록 점성 액체의 흐름을 배열하는 것도 가능하다.^[5] 그러한 흐름은 그 동작에 점성저항이 없다. 이러한 "무궤도 흐름 배열"은 소용돌이처럼 생겼으며 토네이도, 열대성 사이클론, 난기류의 형성에 중요한 역할을 할 수 있다.

프랑들 가설

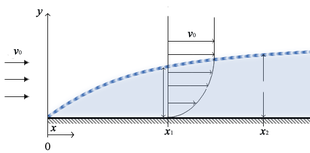
루드비히 프란틀은 경계층의 현대적인 개념을 발전시켰다. 그의 가설은 점도가 낮은 유체의 경우 점도로 인한 전단력은 고체 표면에 인접한 유체의 경계에 있는 얇은 영역에서만 명백하다는 것을 입증한다. 이러한 지역 외부와 양호한 압력 구배가 있는 지역에서는 비스코스 전단력이 없으므로 유체 흐름장은 비결정 유체의 흐름과 동일하다고 가정할 수 있다. Prandtl 가설을 채택함으로써 불규칙한 흐름을 가정하고 고체 주위의 비회전적인 흐름 패턴을 조사함으로써 양호한 압력 기울기의 지역에서 실제 유체의 흐름을 추정할 수 있다.^[6]

실제 유체는 경계층의 분리와 그에 따른 난류성 절제를 경험하지만 이러한 현상은 비결정적 흐름을 사용하여 모델링할 수 없다. 경계 층의 분리는 일반적으로 압력 구배가 유리한 위치에서 불리한 쪽으로 역전되는 경우에 발생하므로 압력 구배가 불리한 지역에서 실제 유체의 흐름을 추정하기 위해 비결정적인 흐름을 사용하는 것이 부정확하다.^[6]

슈퍼플루이드

초유체는 무마찰 유량, 점도가 제로인 물질의 상태를 말하며, 비점성 유량이라고도 한다.^[2]

현재까지 발견된 초유동성을 보이는 유체는 헬륨뿐이다. 헬륨은 람다 포인트로 알려진 지점인 2.2K 이하로 냉각되면 초유체가 된다.^[7] 람다 지점 이상의 온도에서 헬륨은 정상적인 유체 동적 거동을 나타내는 액체로서 존재한다. 일단 2.2K 이하로 냉각되면 양자 행동을 보이기 시작한다. 예를 들어 람다 지점에서는 열 용량이 급격히 증가하는데, 계속 냉각되면서 온도와 함께 열 용량이 감소하기 시작한다.^[8] 또한 열전도도가 매우 커서 초유체 헬륨의 뛰어난 냉각수 특성에 기여한다.^[9]

적용들

분광기는 헬륨을 냉각제로 사용하여 매우 낮은 온도로 유지된다. 이것은 원적외선 판독에서 최소의 배경 유속을 허용한다. 분광계 설계 중 일부는 간단할 수 있지만, 프레임조차 20 켈빈보다 가장 따뜻하다. 이 장치들은 다른 냉각제들보다 초유체 헬륨을 사용하는 것이 매우 비싸기 때문에 일반적으로 사용되지 않는다.^[10]

초유체 헬륨은 열전도율이 매우 높아 초전도체 냉각에 매우 유용하다. LHC(Large Hadron Collider)에서 사용되는 것과 같은 초전도체는 약 1.9 켈빈 온도로 냉각된다. 이 온도는 니오비움-티타늄 자석이 초전도체 상태에 이를 수 있게 한다. 초유체 헬륨을 사용하지 않으면 이 온도가 불가능할 것이다. 이 액체를 사용하는 이러한 온도로 냉각하는 것은 매우 값비싼 시스템이며 다른 냉각 시스템에 비해 거의 없다.^[11]

초유체 헬륨의 또 다른 적용은 양자역학을 이해하는 데 그것의 사용이다. 레이저를 사용하여 작은 물방울을 보는 것은 과학자들이 일반적으로 볼 수 없는 행동을 볼 수 있게 해준다. 이것은 각 방울의 모든 헬륨이 동일한 양자 상태에 있기 때문이다. 이 어플리케이션은 그 자체로 실용적인 용도를 가지고 있지 않지만, 그것은 우리가 그 어플리케이션을 가지고 있는 양자역학을 더 잘 이해할 수 있도록 도와준다.

레이놀즈 수

레이놀즈 번호(Re)는 유체 역학과 공학에서 일반적으로 사용되는 치수 없는 수량이다.^[12][13] 원래 조지 가브리엘 스토크스에 의해 1850년에 묘사된 이 개념은 오스본 레이놀즈에 의해 대중화되었고, 이후 1908년에 아놀드 소머펠트에 의해 그 개념이 명명되었다.^[13][14][15] 레이놀즈 번호는 다음과 같이 계산된다.

${\displaystyle Re={l_{c}v\rho \over \mu}}}}}$

기호	설명	단위
${\displaystyle l_{c}}$	특성 길이	m
${\displaystyle v}$	유체 속도	m/s
$\displaystyle \rho }$	유체 밀도	kg/m3
$\displaystyle \mu }$	유체 점성	파스

이 값은 유체의 점성력에 대한 관성력의 비율을 나타내며 점도의 상대적 중요도를 결정하는 데 유용하다.^[12] 비점성 흐름에서는 점성력이 0이므로 레이놀즈 수가 무한에 접근한다.^[1] 점성력이 무시해도 좋을 때 레이놀즈 수는 1보다 훨씬 크다.^[1] 이러한 경우(Re>>>1) 비결정적 흐름을 가정하면 많은 유체역학 문제를 단순화하는 데 유용할 수 있다.

오일러 방정식

1757년 간행물에서, Leonhard Euler는 비논리적 흐름을 지배하는 일련의 방정식을 설명했다.^[16]

${\displaystyle \rho {D\mathbf {v} \over Dt}=-\nabla p+\rho \mathbf {g}}$

기호	설명	단위
${\displaystyle {D \over Dt}}$	물질적 파생상품
$\displaystyle \nabla }$	델 오퍼레이터
$(\displaystyle p}$	압력을 가하다	파
${\displaystyle \mathbf {g} }$	중력에 의한 가속 벡터	m/s2

비점성 흐름을 가정하면 점성력이 미미한 흐름에는 오일러 방정식을 적용할 수 있다.^[1] 비행기 날개 주위의 흐름, 강의 다리 지지대 주위의 상류 흐름, 그리고 해류를 예로 들 수 있다.^[1]

Navier-Stokes 방정식

1845년 조지 가브리엘 스톡스는 오늘날 나비에 스톡스 방정식으로 알려진 또 다른 중요한 방정식을 발표했다.^[1][17] 클로드루이 나비에르는 분자 이론을 이용하여 먼저 방정식을 개발하였는데, 이는 연속체 이론을 사용하여 스톡스에 의해 더욱 확인되었다.^[1] Navier-Stokes 방정식은 유체의 움직임을 설명한다.^[1]

${\displaystyle \rho {D\mathbf {v} \over Dt}=-\nabla p+\mu \nabla ^{2}\mathbf {v} +\rho \mathbf {g}}}}$

유체가 불규칙하거나 점도가 무시할 수 있다고 가정할 수 있는 경우, Navier-Stokes 방정식은 오일러 방정식으로 단순화된다.^[1] 이러한 단순화는 훨씬 쉽게 해결할 수 있으며 점성이 무시될 정도로 많은 유형의 흐름에 적용될 수 있다.^[1] 비행기 날개 주위의 흐름, 강의 다리 지지대 주위의 상류 흐름, 그리고 해류를 예로 들 수 있다.^[1]

Navier-Stokes 방정식은 $\mu {\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle \mu =0}$일 때 오일러 방정식으로 감소한다$.$ 점성력을 제거하게 하는 또 다른 조건은 $\nabla {\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {}^{}\mathbf{}}$ v${\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle \nabla ^{2}\mathbf {v} =0}$이며$,$ 이로 인해 "비시적 흐름 배열"^[5]이 된다. 그러한 흐름은 소용돌이 같은 것으로 밝혀졌다.

솔리드 경계

주의할 점은 비행기 날개의 경우처럼 더 이상 견고한 경계 근처에서 무시할 수 있는 점도를 가정할 수 없다는 것이다.^[1] 난류 흐름 체계(Re >> 1)에서 점도는 일반적으로 무시될 수 있지만, 이는 솔리드 인터페이스에서 멀리 떨어진 거리에서만 유효하다.^[1] 파이프를 통한 흐름이나 날개 주위의 흐름과 같이 단단한 표면 근처의 흐름을 고려할 때 표면 근처의 흐름의 네 가지 뚜렷한 영역을 분류하는 것이 편리하다.^[1]

• 주요 난류 흐름: 표면에서 가장 멀리 떨어져 있으면 점성이 무시될 수 있다.
• 관성 하위 계층: 주요 난류 흐름의 시작, 점도는 단지 사소한 중요성만을 가지고 있다.
• 버퍼 레이어: 관성층과 점성층 사이의 변환.
• 비스코스 하위 계층: 표면에서 가장 가까운 곳에서 점성이 중요하다.

이러한 구별은 고체 인터페이스 근처에 있는 점성력의 중요성을 설명하는데 유용한 도구가 될 수 있지만, 이러한 영역은 상당히 임의적이라는 점에 유의해야 한다.^[1] 그러나 비결정적 흐름이 많은 유체 역학 문제를 해결하는 데 유용한 도구가 될 수 있다고 가정하면, 이 가정은 고체 경계가 관련되었을 때 유체 하위 계층에 대한 세심한 고려를 요구한다.

참고 항목

• 쿠엣 흐름
• 유체 역학
• 전위 흐름, 비실시 흐름의 특별한 경우
• 스톡스가 흐르는데, 그 안에서 점성력이 관성력보다 훨씬 크다.
• 점도

참조