자카드지수

이 글은 일반적인 참고문헌 목록을 포함하고 있지만, 그에 상응하는 인라인 인용구가 충분하지 않기 때문에 대체로 검증되지 않은 상태로 남아 있다. 보다 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오.(2011년 3월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

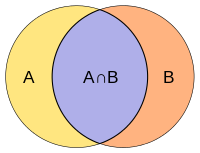
Jaccard 유사 계수라고도 알려진 Jaccard 지수는 표본 집합의 유사성과 다양성을 측정하는 데 사용되는 통계량이다. 원래 프랑스식 이름 계수 de communauté를 부여한 폴 자카드에 의해 개발되었고,^[1] T에 의해 독자적으로 다시 공식화되었다. 타니모토죠^[2] 따라서 타니모토 지수나 타니모토 계수도 일부 분야에서는 사용된다. 그러나, 그들은 일반적으로 유니온에 대한 교차로 비율을 고려하는 데 있어 동일하다. Jaccard 계수는 유한 표본 집합 간의 유사성을 측정하며, 교차점의 크기를 표본 집합의 조합 크기로 나눈 값으로 정의된다.

${\displaystyle J(A,B)={A\cap B}{A\cap B}{A\cup B}={A\cap B}{A\cap B}}}{A\cap B}}}}}이상.}$

Note that by design, ${\displaystyle 0\leq J(A,B)\leq 1.}$ If A and B are both empty, define J(A,B) = 1. The Jaccard coefficient is widely used in computer science, ecology, genomics, and other sciences, where binary or binarized data are used. 정확한 해법과 근사 방법은 모두 자카드 계수를 사용한 가설 시험에 사용할 수 있다.^[3]

자카드 유사성은 가방, 즉 멀티셋에도 적용된다. 이것은 비슷한 공식을 가지고 있지만 ^[4]기호는 가방 교차로와 가방 합을 의미한다. 최대값은 1/2이다.

${\displaystyle J(A,B)={A\cap B }{A\uplus B }}={A\cap B }{A\cap B }}{A\cap B }}}}}.}$

샘플 세트 간의 차이를 측정하는 Jaccard 거리는 Jaccard 계수를 보완하며, 조합의 크기와 두 집합의 교차점 사이의 차이를 조합의 크기로 나누어 Jaccard 계수를 1에서 빼거나 동등하게 구한다.

${\displaystyle d_{J}(A,B)=1-J(A,B)={{ A\cup B - A\cap B}}\over A\cup B}}}$

Jaccard 거리에 대한 대칭차 $A{\displaystyle }$ - B$$ = ( A${\displaystyle \mathrm{△}B}$)${\displaystyle }$-${\displaystyle }$( ${\displaystyle A}$ ${\displaystyle \cap }$ ${\displaystyle B}$) ${\디스플레이$ 스타일 $A\삼각 B=(A\cup B)-(A\cap B)}$의 크기의 비율로 Jaccard 거리를 해석할 수 있다. 자카드 거리는 일반적으로 n 샘플 세트의 클러스터링 및 다차원 스케일링을 위한 n × n 행렬을 계산하는 데 사용된다.

이 거리는 모든 유한 집합의 집합에 대한 미터법이다.^[5][6][7]

확률 측정을 포함한 측정에 대한 Jaccard 거리 버전도 있다. $\mu {\displaystyle }$ ${\displaystyle \mu }$이(가) 측정 가능한 $공간{\displaystyle }$ X$${\$displaystyle X}$에 대한 측정값이라면$$, 다음에 따라 Jaccard 계수를 정의한다$.$

${\displaystyle J_{\mu }(A,B)={{\mu(A\cap B)}\over {\mu(A\cup B)}},}$

그리고 Jaccard 거리 기준

${\displaystyle d_{\mu }(A,B)=1-J_{\mu }{\mu(A,B)={\mu(A\triangle B)}\over {\mu(A\cup B)}}}.}$

이러한 $경우{\displaystyle \mu (}$A ${\displaystyle )\mathrm{B}}$ ) =$$0 {\$displaystyle \mu(A\cup B)=$0} 또는$$$\$ {\$displaystyle$ \$inflt$ $\}$일 경우 이러한 공식은 잘 정의되지 않으므로 주의해야 한다.

각 세트가 해시함수의 최소값에서 파생된 일정한 크기의 서명으로 표현되는 집합 쌍의 Jaccard 유사도 계수의 정확한 추정치를 효율적으로 계산하기 위해 MinHash 최소 독립 순열 로컬리티 해싱 체계를 사용할 수 있다.

비대칭 이항 속성의 유사성

각각 2진수 속성이 n개인 A와 B라는 두 개의 객체를 감안할 때, 자카드 계수는 A와 B가 그들의 속성과 공유하는 중복의 유용한 척도다. A와 B의 각 속성은 0 또는 1일 수 있다. A와 B 모두에 대한 각 속성 조합의 총수는 다음과 같이 지정된다.

${\displaystyle M_{}}$ ${\displaystyle {11}_{}}$ ${\$은 A와 B가 모두 1의 값을 갖는 총 속성 수를 나타낸다$$.

${\displaystyle M_{}}$ ${\displaystyle {01}_{}}$ ${\$은 A의 속성이 0이고 B의 속성이 1인 속성 총수를 나타낸다$$.

${\displaystyle M_{}}$ ${\displaystyle {10}_{}}$ ${\$은 A의 속성이 1이고 B의 속성이 0인 총 속성 수를 나타낸다$$.

${\displaystyle M_{}}$ ${\displaystyle {00}_{}}$ ${\$는 A와 B가 모두 0의 값을 갖는 총 속성 수를 나타낸다$$.

A B	0	1
0	${\displaystyle M_{00}}$	${\displaystyle M_{10}}$
1	${\displaystyle M_{01}}$	${\displaystyle M_{11}}$

각각의 속성은 반드시 이 네 가지 범주 중 하나에 속해야 하는데, 그 의미는 다음과 같다.

${\displaystyle M_{11}+M_{01}+M_{10}+M_{00}=n.}$

Jaccard 유사도 계수 J는 다음과 같이 주어진다.

${\displaystyle J={M_{11} \over M_{01}+M_{10}+M_{11}}}.}$

Jaccard 거리 d는_J 다음과 같이 주어진다.

${\displaystyle d_{J}={M_{01}+M_{10} \over M_{01}+M_{11}=1-J.}$

통계적 추론은 Jaccard 유사도 계수와 그에 따른 관련 지표를 기반으로 할 수 있다.^[3] n 속성이 있는 두 표본 집합 A와 B에 대해, 중복이 통계적으로 유의한지 여부를 확인하기 위해 통계적 시험을 실시할 수 있다. 계산은 n이 증가함에 따라 비용이 많이 들 수 있지만 정확한 해법은 이용할 수 있다.^[3] 추정 방법은 다항 분포 근사치 또는 부트스트래핑을 통해 이용할 수 있다.^[3]

단순 일치 계수(SMC)와의 차이

2진수 속성에 사용할 경우 Jaccard 지수는 단순 일치계수와 매우 유사하다. 주요 차이점은 SMC의 분자와 분모에는$$ M ${\displaystyle {00}_{}}$ ${\$라는 용어가 있지만, 자카드 지수는 그렇지 않다는 것이다. 따라서 SMC는 상호존재(양 세트에 속성이 존재하는 경우)와 상호부재(양 세트에 속성이 없는 경우)를 모두 일치로 계산하고 이를 우주의 총 속성 수와 비교하는 반면, 자카드 지수는 상호존재만 일치로 계산하고 벌이 있는 속성 수와 비교한다.n 두 세트 중 적어도 한 세트에 의해 선택된다.

예를 들어 시장 바스켓 분석에서, 우리가 비교하고자 하는 두 소비자의 바스켓은 매장에서 구할 수 있는 모든 제품의 극히 일부분만 포함하고 있을 수 있으므로, SMC는 바스켓이 거의 유사성이 없을 때에도 매우 높은 유사성 값을 반환하므로, 자카드 지수를 보다 적절한 심리의 척도로 만든다.그런 맥락에서 볼 때 희한함 예를 들어 1000개의 제품과 2개의 고객이 있는 슈퍼마켓을 생각해 보자. 첫 번째 손님의 바구니에는 소금과 후추가 들어 있고, 두 번째 손님의 바구니에는 소금과 설탕이 들어 있다. 이 시나리오에서 자카드 지수에 의해 측정된 두 바구니 사이의 유사도는 1/3이지만 SMC를 사용하여 유사도가 0.998이 된다.

0과 1이 동등한 정보(대칭성)를 전달하는 다른 맥락에서 SMC는 유사성을 더 잘 측정할 수 있다. 예를 들어 성별과 같은 더미 변수에 저장된 인구통계학적 변수의 벡터는 유사성에 대한 성별의 영향이 동일해야 하기 때문에 남성이 0으로 정의되고 여성이 1로 정의되는지 또는 다른 방식으로 정의되는지 여부에 관계없이 자카드 지수보다 SMC와 비교하는 것이 더 나을 것이다. 그러나 대칭 인체모형 변수가 있는 경우 인체모형을 두 개의 이항 속성(이 경우 남성과 여성)으로 분할하여 비대칭 속성으로 변환하여 편향 없이 자카드 지수를 사용할 수 있게 함으로써 SMC의 행동을 복제할 수 있다. 그러나 SMC은 추가 치수를 추가하지 않아도 되기 때문에 대칭 더미 변수의 경우 계산적으로 더 효율적이다.

가중 자카드 유사성 및 거리

If ${\displaystyle \mathbf {x} =(x_{1},x_{2},\ldots ,x_{n})}$ and ${\displaystyle \mathbf {y} =(y_{1},y_{2},\ldots ,y_{n})}$ are two vectors with all real ${\displaystyle x_{i},y_{i}\geq 0}$, then their Jaccard similarity coeffefficient(당시 루지카 유사성이라고도 함)는 다음과 같이 정의된다.

${\displaystyle J_{\mathbf {x},\mathbf {y}}={\frac {\sum {\i}\min(x_{i}y_{i}}}}})}}{\sum _{i}\max(x_{i}},y_{i}}}}},}$

자카드 거리(당시 소에르겔 거리라고도 함)

${\displaystyle d_{J{\mathbal {W}(\mathbf {x},\mathbf {y} )=1-J_{\mathbcal {W}(\mathbf {x},\mathbf {y}).}$

보다 일반성으로 $f{\displaystyle }$ ${\displaystyle f}$과 g ${\displaystyle g}$이(가$)$ 측정 가능한 공간 $X{\displaystyle }$ ${\displaystyle$$X}$에서 측정 가능한 두 개의 비음수 함수라면$$, 우리는 정의할 수 $있다$

${\displaystyle J_{\mathcal{W}(f,g)={\frac {\int \min(f,g)d\mu}{\int \max(f,g)d\},}$

여기서 ${\displaystyle max}$ ${\displaystyle \max }$과 ${\displaystyle min}$ ${\displaystyle \min }$은(는) 포인트와이즈 연산자다. 그러면 자카드 거리는

${\displaystyle d_{J{\mathcal{W}}(f,g)=1-J_{\mathcal{W}(f,g).}$

Then, for example, for two measurable sets ${\displaystyle A,B\subseteq X}$, we have ${\displaystyle J_{\mu }(A,B)=J(\chi _{A},\chi _{B}),}$ where ${\displaystyle \chi _{A}}$ and ${\displaystyle \chi _{B}}$ are the characteristic functions of the corresp온더링 세트

확률 자카드 유사성 및 거리

위에서 설명한 가중 Jaccard 유사성은 Jaccard Index를 양의 벡터에 일반화하며, 여기서 집합은 표시기 함수에 의해 주어진 이항 벡터에 해당한다($예{\displaystyle {}_{}}$: x ${\displaystyle i_{}}$ ${\displaystyle {}_{}}${ ${\displaystyle 0,}$ ${\displaystyle 1}$} ${\displaystyle x_{i}\in$$\{0,1\}).$ 그러나 집합이 확률 분포에 해당하는 경우에는 일반화되지 않는다. 균일한 확률 분포, 즉

${\displaystyle x_{i}={\begin{case}{\frac {1}{X }}}{X\\\no\texture}\otherwise}\end{case}}}}}}$

세트의 크기가 다르면 항상 작다. If ${\displaystyle X > Y }$, and ${\displaystyle x_{i}=\mathbf {1} _{X}(i)/ X ,y_{i}=\mathbf {1} _{Y}(i)/ Y }$ then

${\displaystyle J_{\mathcal{W}(x,y)={\frac {X\cap Y}{X\setminus Y + X }}}}<J(X,Y)}}$

대신 확률 분포와 그에 상응하는 지지 집합 사이에 연속적인 일반화는 다음과 같다.

${\displaystyle J_{\mathcal {P}}(x,y)=\sum _{x_{i}\neq 0,y_{i}\neq 0}{\frac {1}{\sum _{j}\max \left({\frac {x_{j}}{x_{i}}},{\frac {y_{j}}{y_{i}}}\right)}}}$

'^[8]확률성' 자카드라 불리는 거야 확률 벡터에 대한 가중 자카드에 대해 다음과 같은 한계가 있다.

${\displaystyle J_{\mathcal {W}(x,y)\leq J_{P}}\frac {2J_{\mathcal {W}{1+J_{\mathcal {W}}{\mathcal {W}}}}{\mathcal {W}}}}}}}}$

여기서 상한은 (가중치) 쇠렌센-디체 계수다. 해당 거리인 $1{\displaystyle \mathrm{}}$- J ${\displaystyle P_{}}$( ${\displaystyle x}$, y${\displaystyle }$) ${\displaystyle 1-J_{\mathcal{P}}(x,y$는 확률 분포에 대한 메트릭이고, 비음수 벡터에 대한 유사 메트릭이다.

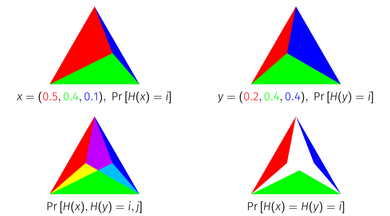
확률 자카드 지수는 단순함의 교차점 영역으로서 기하학적 해석을 가지고 있다. 단위 $k{\displaystyle }$ ${\displaystyle k}$ -simplex의$$ 모든 점은 $k{\displaystyle }$+ ${\displaystyle 1}$원소의$$ 확률 분포에 해당하는데, 그 이유는 $단위{\displaystyle }$ k ${\displaystyle$k$}$ -simplex는$$ ${\displaystyle 1}$에 합한 k${\displaystyle }$+ 1 {\$displaystyle k+1}$ 치수의$$ 점 집합이기 때문이다$.$ 확률 자카드 지수를 기하학적으로 도출하려면 각 항목의 질량에 따라 단위 심플렉스(simplex)를 하위 단순화로 나눈 확률 분포를 나타낸다. 이런 식으로 표현된 두 개의 분포를 서로 겹쳐 놓고 각 항목에 해당하는 단순화를 교차하는 경우 남아 있는 면적은 분포의 확률 자카드 지수와 동일하다.

확률 자카드 지수의 최적성

랜덤 변수가 서로 최대한 충돌하도록 구성하는 문제를 고려하십시오. That is, if ${\displaystyle X\sim x}$ and ${\displaystyle Y\sim y}$, we would like to construct ${\displaystyle X}$ and ${\displaystyle Y}$ to maximize ${\displaystyle \Pr[X=Y]}$. If we look at just two distributions ${\displaystyle x,y}$ in isolation, the highest ${\displaystyle Pr[X=}$${\displaystyle Y}$ ${\displaystyle ]}$ ${\displaystyle \Pr[X=Y]}$이(가) $1{\displaystyle \mathrm{}}$- ${\displaystyle \text{TV}(x}$, y )${\displaystyle 1-{\text{$$TV$$}(x,y)},$ ${\displaystyle \text{여기}}$서 TV$${\$displaystyle${\$text}$$TV}}$은(는) 총 변동 거리 입니다. 그러나 특정 쌍을 최대화하는 데만 관심을 두지 않았다고 가정해 보십시오. 임의 쌍의 충돌 확률을 최대화하고 싶다고 가정해 보십시오. 각 분포 $x{\displaystyle }$ ${\displaystyle x}$에 대해 무한히 많은 수의 랜덤 변수를 구성할 수 있으며$,$ 모든 쌍 $x{\displaystyle }$, ${\displaystyle y}$ ${\displaystyle x,y}$에 대해 ${\displaystyle Pr}$[$X=Y]$를 최대화할 수 있다$.$ 아래에서 설명하는 상당히 강력한 의미에서 확률 자카드 지수는 이러한 랜덤 변수를 정렬하는 최적의 방법이다.es.

모든 표본 추출 $방법{\displaystyle }$ G$${\$displaystyle$$$G$\}$$$및 이산$$ $분포{\displaystyle }$ x${\displaystyle }$,$$[ ( )= ( ) > P( , y) ${\displaystyle \Pr[G(x)=G(y)]$일 $>J_{\mathcal{P}(x,$$)}$ 그러면 일부 $z{\displaystyle }$ ${\displaystyle z}$ 여기서$$ J ( ,) ${\displaystyle J_{\mathcal {P}(x,z)}$$J_{\mathcal {{P}(x,y)}$과(와) P (, z)> ( , $){\displaystyle J_{\mathcal{P}}(y,z)$ > 입니다.$J_{\mathcal {{P}($$,y$ [ G( )= G( ) < ( , ) ${\displaystyle \Pr[G(x)=G(z)]$ 중 하나$<J_{\mathcal{P}}(x,z)}$ [ G() = ( ) < P ( , ) ${\displaystyle \Pr[G(y)=G(z)]]$$<J_{\mathcal{P}(y,z$^[8]

즉, 감소된 쌍이 $증가$된 ${\displaystyle {파이}_{}}$보다 J P ${\$$displaystyle J_{\mathcal$${P$$}$보다 더 유사한 다른 쌍에서$$ $J{\displaystyle {}_{}}$ ${\displaystyle {P\mathcal{}}_{}}$ ${\$ {$P}$보다 적은 충돌을 달성하지 않고 한 쌍에서$$ $J{\displaystyle {}_{}}$ P ${\$$displaystyle J_{\\\\mathcal}$보다 더 큰 충돌을 달성할 수 있는 방법은 없다.r. 이 정리는 집합의 자카드 지수(일률 분포로 해석되는 경우)와 확률 자카드에 대해 사실이지만 가중된 자카드의 경우는 아니다.(정리는 "샘플링 방법"이라는 단어를 사용하여 공간상의 모든 분포에 대한 공동 분포를 기술하는데, 이는 달성하는 가중 축소 알고리즘의 사용에서 기인하기 때문이다. 이들의 충돌 확률로 이 점을 고려되어야 한다.

이 정리는 심플렉스 표현을 사용한 세 가지 요소 분포에 대한 시각적 증거를 가지고 있다.

타니모토 유사성과 거리

타니모토 유사성과 타니모토 거리로 묘사된 다양한 형태의 기능들이 문헌과 인터넷에서 발생한다. 이 중 대부분은 자카드 유사성과 자카드 거리에 대한 동의어지만 수학적으로 다른 것도 있다. 많은 소식통들은^[9] IBM 기술 보고서를^[2] 중요한 참고 자료로 인용한다. 그 보고서는 여러 도서관에서 구할 수 있다.

1960년 10월에 발간된 「식물 분류용 컴퓨터 프로그램」에서는 유사율에 근거한 분류 방법, 파생 거리 함수를 제시한다.^[10] '타니모토 유사성'과 '타니모토 거리'라는 용어의 의미를 알 수 있는 가장 권위 있는 출처인 것 같다. 유사도는 자카드 유사성에 해당하지만 거리 함수는 자카드 거리와 같지 않다.

유사성과 거리에 대한 타니모토의 정의

이 논문에서 "유사성 비율"은 비트맵을 통해 주어지며, 여기에서 고정 크기 배열의 각 비트는 모델링되는 발전소의 특성의 유무를 나타낸다. 비율의 정의는 공통 비트의 수를 두 표본의 비트 세트 수(즉, 0이 아닌 비트 수)로 나눈 값이다.

수학적 용어로 표현하면 표본 X와 Y가 비트맵인 경우 $X{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$는 X의 ith 비트, ∧${\displaystyle }$,${\displaystyle \vee }$ ${\displaystyle \land ,\lor }$은(는) 비트 및 연산자, 즉 유사비 T ${\displaystyle s_{}}$ ${\$는 다음과 같다.

${\displaystyle T_{s}(X,Y)={\frac {\sum _{i}(X_{i}\land Y_{i}}}}{\sum _{i}}}}{\sum _{i}}}}}}}}$

각 표본을 속성 집합으로 대신 모델링할 경우, 이 값은 두 집합의 자카드 계수와 동일하다. Jaccard는 논문에서 인용되지 않았으며, 저자들이 몰랐을 가능성이 있어 보인다.

Tanimoto는 계속해서 0이 아닌 유사성을 가진 비트맵에 대해 정의된 이 비율을 바탕으로 "거리 계수"를 정의한다.

${\dplaystyle T_{d}(X,Y)=-\log _{2}(T_{s}(X,Y))}$

이 계수는 고의적으로 거리측정이 아니다. 서로 상당히 다른 두 표본이 둘 다 3분의 1과 비슷할 수 있도록 하기 위해 선택된다. 삼각 불평등의 속성을 반증하는 예를 구성하기는 쉽다.

타니모토 거리의 기타 정의

타니모토 거리를 흔히 자카드 거리 $1{\displaystyle \mathrm{}}$- ${\displaystyle T_{}}$ s ${\$의 동의어로 잘못 언급한다$.$ 이 함수는 적절한 거리 측정 기준이다. 「타니모토 거리」는, 자카드 거리와의 혼동 때문인지, 적절한 거리 측정법으로 언급되는 경우가 많다.

자카드나 타니모토 유사성이 비트 벡터 위에 표현된다면, 라고 쓸 수 있다.

${\displaystyle f(A,B)={\frac {A\cdot B}{\A\cdot B}{\\{2}+\B\{2}-A\cdot B}}}}$

여기서 동일한 계산이 벡터 스칼라 제품 및 크기 단위로 표현된다. 이 표현은 비트 벡터(각 차원의 값이 0 또는 1)에 대해 다음이라는 사실에 의존한다.

$B=\sum _{i}A_{i}B_{i}=\sum _{i}(A_{i}\land B_{i})}$

그리고

${\displaystyle \ A\ ^{2}=\sum _{i}A_{i}^{2}=\sum _{i}A_{i}}$

이는 벡터를 통해 표현된 함수가 명시적으로 제한되지 않는 한 더 일반적이기 때문에 잠재적으로 혼란스러운 표현이다. $T{\displaystyle {}_{}}$ ${\displaystyle s_{}}$ ${\$의 속성은 반드시 $f{\displaystyle }$ ${\displaystyle f}$까지 확장되는 것은 아니며$$$,$ 특히 ${\displaystyle \mathrm{차이}}$ 함수 $1{\displaystyle \mathrm{}}$- f ${\displaystyle 1-f}$는 삼각 불평등을 보존하지 않으며$$, 따라서 적절한 거리 메트릭이 아닌 반면에 $1{\displaystyle \mathrm{}}$- ${\displaystyle T_{}}$ ${\$는 다음과 같다.

"타니모토 거리는 적절한 거리 측정 기준"이라는 문구와 함께 이 공식을 사용하여 정의되는 "${\displaystyle \mathrm{타니모토}}$ 거리"의 조합은 함수 $1{\displaystyle \mathrm{}}$- f$[\디스플레이$ 스타일 $1-f}$가 사실상 벡터나 멀티셋에 대한 거리 측정 기준인$$ 반면, 시미에서는 사용된다는 잘못된 결론을 초래할 실제 위험이 있다.친절도 검색 또는 클러스터링 알고리즘이 정확한 결과를 생성하지 못할 수 있다.

Lipkus[6], 다니모토 거리에 기능 1− f{1-f\displaystyle}로 언급한다. 그러나, 명확한 종이 안에서 컨텍스트 W는(긍정적인)가중치 벡터의 사용과{W\displaystyle}, 대한 제한되어 있었다 다니모토 유사성의 f{\displaystyle f}과 동등한 정의를 사용한다.vyexter A 고려 대상, A i${\displaystyle i_{}}$ { 0${\displaystyle ,}$ ${\displaystyle {}_{}}$ ${\displaystyle i_{}\}.}$ ${\displaystyle A_{i}\in \{0,$$W_{i}\}.}$이러한$$ 상황에서 함수는 적절한 거리 메트릭이므로 그러한 가중 벡터에 의해 지배되는 벡터 집합이 이 함수 아래 메트릭 공간을 형성한다.

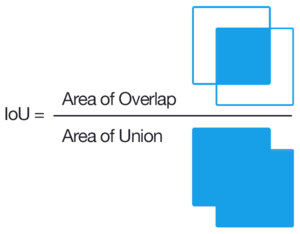
이진 분류 혼동 행렬의 자카드 색인

이항 분류를 위해 사용되는 혼동 행렬에서 자카드 지수는 다음과 같은 공식으로 프레임을 설정할 수 있다.

${\displaystyle {\text{Jaccard index}={\frac {TP}{TP+FP+FN}}$

여기서 TP는 참 긍정이고 FP는 거짓 긍정이며, FN은 거짓 부정이고 TN은 참 부정일 것이다.^[11]

참고 항목

• 겹침 계수
• 단순매칭계수
• 해밍 거리
• Sørensen–Dice coefficient, which is equivalent: ${\displaystyle J=S/(2-S)}$ and ${\displaystyle S=2J/(1+J)}$ (${\displaystyle J}$: Jaccard index, ${\displaystyle S}$: Sørensen–Dice coefficient)
• 트베르스키 지수
• 상관 관계
• 상호 정보, 계량화된 정규화된 변종이며, 이 변종은 등방성 Jaccard 거리이다.

참조

추가 읽기

외부 링크

• Tan, Steinbach, Kumar의 데이터 마이닝 강의 노트 소개
• SimMetrics Jaccard 인덱스 및 기타 유사성 측정 기준의 원천 구현
• Jaccard 계수를 찾기 위한 웹 기반 계산기
• 서로 다른 유사점을 계산하는 방법에 대한 자습서
• 객체 탐지를 위한 IoU(조합을 통한 교차점)
• Kaggle Dstl 위성 이미지 기능 탐지 - 평가