양자 물리학의 모형
양자역학 에서, 1차원 격자의 입자 는 주기적인 결정 격자 모형에서 발생하는 문제입니다.전위는 결정 의 주기적 구조에서 전자장을 생성 하는 이온에 의해 발생하므로 전자는 격자 안에서 일정한 전위에 노출됩니다. 이것은 격자 내부 의 0 전위를 가정하는 자유 전자 모델의 일반화입니다.
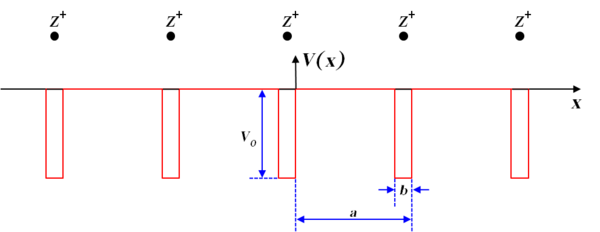
문제의 정의 고체 재료에 대해 이야기할 때, 주로 결정, 즉 주기적인 격자에 대해 논의합니다. 여기서는 양이온의 1D 격자에 대해 설명하겠습니다. 두 이온 사이의 간격이 a 라고 가정하면 격자의 전위는 다음과 같습니다.
전위의 수학적 표현은 주기 a를 갖는 주기 함수이다. 블로흐의 [1] 슈뢰딩거 방정식의 파동함수 해는 다음과 같이 쓸 수 있다.
ψ ( x ) = e i k x u ( x ) , \displaystyle \psi(x)=e^{ikx}u(x),}
여기 u(x )(x + a ) = u x )만족 주기 함수이다.플로케트 지수 displaystyle )
격자의 가장자리에 가까워지면 경계 조건에 문제가 있습니다. 따라서, 우리는 Born-von Karman 경계 조건 을 따르는 고리로서 이온 격자를 나타낼 수 있다. L 길이 격자 내의 이온수가 매우 커서 하나의 이온을 고려할 때 그 주변은 거의 선형이며 전자의 파동함수는 변하지 않는다.따라서 두 개의 경계 조건 대신 하나의 원형 경계 조건이 생성됩니다.
ψ ( 0 ) = ψ ( L ) . \displaystyle \psi (0)=\psi (L). }
N 이 격자에 있는 이온의 수일 경우, 다음과 같은 관계가 있습니다 aN k :
ψ ( 0 ) = e i k ⋅ 0 u ( 0 ) = e i k L u ( L ) = ψ ( L ) \displaystyle \psi (0)=e^{ik\cdot 0}u (0)=e^{ikL}u (L)=\psi (L)} u ( 0 ) = e i k L u ( L ) = e i k L u ( N a ) → e i k L = 1 \displaystyle u(0)=e^{ikL}u(L)=e^{ikL}u(Na)\to e^{ikL}=1} ⇒ k L = 2 π n → k = 2 π L n ( n = 0 , ± 1 , … , ± N 2 ) . (\displaystyle \rightarrow kL=2\pi n\to k={2\pi \over L}n\qquad \left(n=0,\pm 1,\displays,\pm {N}{2}}\pm). }
크로니그-페니 모델 크로니그-페니 모델(Ralph Kronig와 William [2] 이름 을 따서 명명)은 직사각형 전위 장벽의 무한 주기 배열로 구성된 단순하고 이상적인 양자역학 시스템입니다.
퍼텐셜 함수는 직사각형 퍼텐셜로 근사됩니다.
Bloch의 정리 를 사용하면, 우리는 단지 하나의 주기에 대한 해답을 찾고, 그것이 연속적이고 매끄러운지 확인하고, 그리고 함수 x )
잠재력이 있는 단일 기간을 고려: 여기에는 두 개의 지역이 있습니다. 각각 개별적으로 해결합니다.E를 우물 위의 에너지 값(E >0)으로 합니다.
0 x a b displaystyle x 경우 − ℏ 2 2 m ψ x x = E ψ ⇒ ψ = A e i α x + A ′ e − i α x ( α 2 = 2 m E ℏ 2 ) {\displaystyle {\frac {-\hbar ^{2}}{2m}}\psi _{x}&=E\psi \\rightarrow \psi &=Ae^{i\alpha x}+ A'e^{-i\alpha x}&\left(\alpha ^{2}={2mE \over \hbar ^{2}}\right)\end{aligned}}} - b x 0 display style x 0 : − ℏ 2 2 m ψ x x = ( E + V 0 ) ψ ⇒ ψ = B e i β x + B ′ e − i β x ( β 2 = 2 m ( E + V 0 ) ℏ 2 ) . ({displaystyle {-\hbar ^{2}}{2m}}\psi _{xx}&=(E+V_{0})\psi \\\rightarrow \psi &=Be^{i\beta x}+B'e^{-i\beta x}&\left(\{2m})\(\fsi) \end { aligned}} 각 영역에서 u(x )를 찾으려면 전자의 파동 함수를 조작해야 합니다.
ψ ( 0 < > x < > a − b ) = A e i α x + A ′ e − i α x = e i k x ( A e i ( α − k ) x + A ′ e − i ( α + k ) x ) ⇒ u ( 0 < > x < > a − b ) = A e i ( α − k ) x + A ′ e − i ( α + k ) x . {\displaystyle}\psi (0<x<a-b)& =Ae^{i\alpha x}+ A'e^{-i\alpha x}=e^{ikx}\left(Ae^{i(\alpha -k)x}+ A'e^{-i(\alpha +k)x}\오른쪽 화살표 u(0<x<a-b)& =Ae^{i(\alpha -k)x}+ A'e^{-i(\alpha +k)x}. \end { aligned}}
그리고 같은 방식으로:
u ( − b < > x < > 0 ) = B e i ( β − k ) x + B ′ e − i ( β + k ) x . {\displaystyle u\b<x<0) =Be^{i(\beta -k)x}+ B'e^{-i(\beta +k)x} }
솔루션을 완성하기 위해서는 확률 함수가 연속적이고 매끄러운지 확인해야 합니다.
ψ ( 0 − ) = ψ ( 0 + ) ψ ′ ( 0 − ) = ψ ′ ( 0 + ) . \displaystyle \psi (0^{-})=\psi (0^{+})\qquad \psi ' (0^{-})=\psi ' (0^{+}). }
그리고 (x ) 와 u( x )
u ( − b ) = u ( a − b ) u ′ ( − b ) = u ′ ( a − b ) . {\displaystyle uhb}=u(a-b)\qquad u'(-b)=u'(a-b)입니다. }
이러한 조건에 의해, 다음의 매트릭스가 생성됩니다.
( 1 1 − 1 − 1 α − α − β β e i ( α − k ) ( a − b ) e − i ( α + k ) ( a − b ) − e − i ( β − k ) b − e i ( β + k ) b ( α − k ) e i ( α − k ) ( a − b ) − ( α + k ) e − i ( α + k ) ( a − b ) − ( β − k ) e − i ( β − k ) b ( β + k ) e i ( β + k ) b ) ( A A ′ B B ′ ) = ( 0 0 0 0 ) . {\displaystyle{\begin{pmatrix}1&, 1&, -1&, -1\\\alpha&-\alpha&-\beta&\beta \\e^{i(\alpha -k)(a-b)}&, e^{-i(\alpha +k)(a-b)}&, -e^{-i(\beta -k)b}&, -e^ᆼ\\(\alpha -k)e^{i(\alpha -k)(a-b)}&, -(\alpha +k)e^{-i(\alpha +k)(a-b)}&, -(\beta -k)e^{-i(\beta -k)b}&,(\beta +k)e^{i(\beta +k)b}\end{pmatrix}}{\begin.{pmatrix} A\\A'\B\ B'\end{pmatrix}="begin{pmatrix}0\\0\\0\end{pmatrix}" }
우리가 사소하지 않은 해를 가지기 위해서는 행렬의 행렬식이 0이어야 한다. 그러면 다음과 같은 표현이 나옵니다.
왜냐하면 ( k a ) = 왜냐하면 ( β b ) 왜냐하면 [ α ( a − b ) ] − α 2 + β 2 2 α β 죄 ( β b ) 죄 [ α ( a − b ) ] . \displaystyle \cos(ka)=\cos(\cos(\cos(\cos(b)))\cos[\alpha (a-b)]-{\alpha ^{2}+\alpha ^{2}\over 2\alpha \cos }\sin[\alpha (a-b)] }
식을 더욱 단순화하기 위해 다음과 같은 근사치를 수행합니다.
b → 0 ; V 0 → ∞ ; V 0 b = c o n s t a n t {\displaystyle b\to 0;\display V_{0}\to\infty;\display V_{0}b=\mathrm {display}} ⇒ β 2 b = c o n s t a n t ; α 2 b → 0 {\displaystyle \Rightarrow \mathrm {b};\displaystyle \alpha ^{2}b\to 0} ⇒ β b → 0 ; 죄 ( β b ) → β b ; 왜냐하면 ( β b ) → 1. \displaystyle \Rightarrow \beta b\to 0;\quad \sin(\beta b)\to \beta b;\quad \cos(\beta b)\to 1.
표현은 다음과 같습니다.
왜냐하면 ( k a ) = 왜냐하면 ( α a ) + P 죄 ( α a ) α a , P = m V 0 b a ℏ 2 . \displaystyle \cos(ka)=\cos(\alpha a)+ P{\frac {sin(\alpha a)}{\alpha a}},\qquad P=mV_{0}ba}{\hbar ^{2}}. }
우물 내부의 에너지 값(E < 0)은 다음과 같습니다.
왜냐하면 ( k a ) = 왜냐하면 ( β b ) 아늑하다 [ α ( a − b ) ] − β 2 − α 2 2 α β 죄 ( β b ) 신 [ α ( a − b ) ] , \displaystyle \cos(ka)=\cos(\cos(\cos(b))\cosh[\alpha (a-b)]-{\alpha ^{2}\over 2\alpha \alpha }\sinh[\alpha (a-b)},} α = 2 m ℏ displaystyle \alpha 2 \over \hbar ^{2} β = 2 V E displaystyle \hbar } 2 V 2 displaystylash frac
위와 같은 근사치(b → 0 , V → V 0 = c o t n displaystyle b\to 0;, V_{0}b=\mathrm })
왜냐하면 ( k a ) = 아늑하다 ( α a ) + P 신 ( α a ) α a \displaystyle \cos(ka)=\cosh(\alpha a)+ P{\frac {\alpha a}{\alpha a}} (P = m V b 2 )\ style \left(P specfrac mV_{0} ^{2}}\ })\ specfrac {0 light
크로니그-페니 모델의 밴드 간격 분산 관계에서 cos(k a)가 동일한 식의 값으로, P = 1.5입니다. 검은색 막대는 k를 계산할 수 있는 α 영역 . 크로니그-페니 모형의 분산 관계이며, P = 1.5입니다. 전 항에서 물리적 시스템의 매개변수에 의해 결정되지 않은 변수는 에너지 E와 결정 운동량 k뿐입니다. E의 값 을 선택하면 오른쪽을 계산하고, 그 다음 양쪽의 아크코 (\ \arccos) 계산 할 수 있다. 따라서 이 표현은 분산 관계 를 일으킨다.
위의 마지막 식 오른쪽이 1보다 크거나 -1보다 작을 수 있습니다.이 경우 방정식을 성립시킬 수 있는k 값 은 없습니다. α e displaystyle \alpha propto sqrt E α 특정값 이 존재함을 의미합니다.이들 값은 밴드갭을 구성합니다.
따라서 크로니그-페니 모델은 밴드 갭을 나타내는 가장 단순한 주기적 전위 중 하나이다.
Kronig-Penney 모델: 대체 솔루션 유사한 문제에 대한 대체 치료법이 제시되었다. 여기 델타 주기 퍼텐셜이 있습니다.
V ( x ) = A ⋅ ∑ n = − ∞ ∞ δ ( x − n a ) . {\displaystyle V(x)= A\cdot \sum _{n=-\infty}^{\infty}\cdot (x-na). }
A는 일정한 상수 이고, a는 격자 상수(각 사이트 사이의 간격)입니다. 이 전위는 주기적이므로 푸리에 급수로 확장할 수 있습니다.
V ( x ) = ∑ K V ~ ( K ) ⋅ e i K x , {\displaystyle V(x)=\sum _{K}{\tilde {V}}(K)\cdot e^{iKx}} 어디에 V ~ ( K ) = 1 a ∫ − a / 2 a / 2 d x V ( x ) e − i K x = 1 a ∫ − a / 2 a / 2 d x ∑ n = − ∞ ∞ A ⋅ δ ( x − n a ) e − i K x = A a . ({displaystyle {V}}(K)=paramfrac {1}{a}}\int _{-a/2}^{a/2}dx,V(x),e^{-iKx}=paramfrac {1}{a}\int _{a/2}^{a/2}^{n=infty}^{n=infty})^{n=infty}{a}{a}^{-fty}) }
블로흐의 정리를 사용하는 파동함수는 θ x = e i x u x displaystyle \psi k}(x e^{ikx}u_ {k}( x x)
u k ( x ) = ∑ K u ~ k ( K ) e i K x . {\displaystyle u_{k}(x)=\sum _{K}{\tilde {u}_{k}(K)e^{iKx}}}
따라서 파동 함수는 다음과 같습니다.
ψ k ( x ) = ∑ K u ~ k ( K ) e i ( k + K ) x . \displaystyle \psi _{k}(x)=\sum _{K}{\tilde {u}_{k}(K), e^{i(k+K)x}. }
이를 슈뢰딩거 방정식에 대입하면 다음과 같은 결과를 얻을 수 있습니다.
[ ℏ 2 ( k + K ) 2 2 m − E k ] u ~ k ( K ) + ∑ K ′ V ~ ( K − K ′ ) u ~ k ( K ′ ) = 0 \displaystyle \left[{\frac {hbar ^{2}(k+K)^{2] }{2m}-E_{k}\right]{\tilde {u}_{k}(K)+\sum _{K'}{\tilde {V}(K-K'),{\tilde {u}_{k}(K')=0} 또는 오히려: [ ℏ 2 ( k + K ) 2 2 m − E k ] u ~ k ( K ) + A a ∑ K ′ u ~ k ( K ′ ) = 0 \displaystyle \left[{\frac {hbar ^{2}(k+K)^{2] }{2m}-E_{k}\right]{\tilde {u}_{k}(K)+{\frac {A}{a}}\sum _{K'}{\tilde {u}_{k}(K')=0}
이제 우리는 다음을 인식합니다.
u k ( 0 ) = ∑ K ′ u ~ k ( K ′ ) {\displaystyle u_{k}(0)=\sum _{K'}{\tilde {u}_{k}(K')}}}
이를 슈뢰딩거 방정식에 대입합니다.
[ ℏ 2 ( k + K ) 2 2 m − E k ] u ~ k ( K ) + A a u k ( 0 ) = 0 \displaystyle \left[{\frac {hbar ^{2}(k+K)^{2] }{2m}-E_{k}\right]{\tilde {u}_{k}(K)+{\frac {A}{a}}u_{k}(0)=0}
u k displaystyle { tilde u} k u
u ~ k ( K ) = 2 m ℏ 2 A a f ( k ) 2 m E k ℏ 2 − ( k + K ) 2 = 2 m ℏ 2 A a 2 m E k ℏ 2 − ( k + K ) 2 u k ( 0 ) {\displaystyle {\tilde {u}_{k}(K)=par frac {\frac {2m}{\hbar ^{2}}{\frac {A}{a}f(k)}{\frac {2mE_{k}}{\hbar ^2}-(K){\hbar } }}}=par frac {\frac {2m}{\hbar ^{2}}{\frac {A}{a}}}{\frac {2mE_{k}}{\hbar ^{2}}-(k+K)^2} }}},u_{k}(0)}
이 마지막 방정식을 K의 모든 값에 대해 합산하면 다음과 같습니다.
∑ K u ~ k ( K ) = ∑ K 2 m ℏ 2 A a 2 m E k ℏ 2 − ( k + K ) 2 u k ( 0 ) {\displaystyle \sum _{K}{\tilde {u}(K)=\sum _{K}{\frac {2m}{\hbar ^{2}}{\frac {A}{a}}}}{\frac {2mE_{k}}{\hbar ^2}+K^2}{\frc} }}},u_{k}(0)}
또는 다음 중 하나를 선택합니다.
u k ( 0 ) = ∑ K 2 m ℏ 2 A a 2 m E k ℏ 2 − ( k + K ) 2 u k ( 0 ) {\displaystyle u_{k}=\sum _{K}{\frac {2m}{\hbar ^{2}}{\frac {A}{a}}}{\frac {2mE_{k}}}{\hbar ^{2}-(k+K)^2} }}},u_{k}(0)}
편리하게도 u 0 display u k 0
1 = ∑ K 2 m ℏ 2 A a 2 m E k ℏ 2 − ( k + K ) 2 {\displaystyle 1=\sum _{K}{\frac {2m}{\hbar ^{2}}{\frac {A}{a}}{\frac {2mE_{k}}{\hbar ^{2}}-(k+K)^2}{\hbar } }}}}
또는 다음 중 하나를 선택합니다.
ℏ 2 2 m a A = ∑ K 1 2 m E k ℏ 2 − ( k + K ) 2 {\displaystyle {\frac ^{2}} {2m} {\frac {a} { A}}=\sum _{K}{\frac {1}{\frac {2mE_{k}}{\hbar ^{2}}-(k+K)^{2 }}}}
불필요한 알림 작업을 줄이기 위해 새로운 변수를 정의합니다.
α 2 := 2 m E k ℏ 2 (\displaystyle \alpha ^{2}:=frac {2mE_{k}}{\hbar ^{2}}}) 마지막으로 우리의 표현은 다음과 같습니다. ℏ 2 2 m a A = ∑ K 1 α 2 − ( k + K ) 2 {\displaystyle {\frac ^{2}} {2m} {\frac {a} { A}}=\sum _{K}{\frac {1}{\alpha ^{2}-(k+K)^{2 }}}}
K 는 역격자 벡터입니다. 즉, 실제로는 K에 대한 합이 2µ displaystyle {2\pi a
ℏ 2 2 m a A = ∑ n = − ∞ ∞ 1 α 2 − ( k + 2 π n a ) 2 {\displaystyle {\frac ^{2}} {2m} {\frac {a} { A}}=\sum _{n=-\infty}^{\infty}{\frac {1}{\alpha ^{2}-(k+{\frac {2\pi n}{a}})^{2}}}}}}
이 식을 조금 더 암시적으로 만들 수 있습니다(부분 부분 분해 를 사용).
ℏ 2 2 m a A = ∑ n = − ∞ ∞ 1 α 2 − ( k + 2 π n a ) 2 = − 1 2 α ∑ n = − ∞ ∞ [ 1 ( k + 2 π n a ) − α − 1 ( k + 2 π n a ) + α ] = − a 4 α ∑ n = − ∞ ∞ [ 1 π n + k a 2 − α a 2 − 1 π n + k a 2 + α a 2 ] = − a 4 α [ ∑ n = − ∞ ∞ 1 π n + k a 2 − α a 2 − ∑ n = − ∞ ∞ 1 π n + k a 2 + α a 2 ] \displaystyle {\frac ^{2}} {2m} {\frac {a} { A}}&=\sum _{n=-\infty}^{\infty}{\frac {1}-(k+{\frac {2\pi n}{a})^{2}}\&={\frac {1}{2\alpha }}}\sum {n=-infty}^{\fty}{\fty } \&=-{\frac {a}{4\alpha}}\sum _{n=-\infty}^{\infty}\left[{\frac {1}{\pi n+{ka}{2}}-{\frac {\frac {1}-{\pi n+{2}}}-{\frac {\frac {\frac}}{{frac}}}{frac {frac}}}}{frac {frac {frac {frac}}}}} {frac {frac}}}}{\frac { \&=-{\frac {a}{4\alpha}}\left[\sum _ {n=-\infty }^{\infty }{\frac {1}{\pi n+{\frac {ka}{2}}-{\sum _ n=-\infty }{frac {frac} {1}
코탄젠트 함수(등식 18 )의 합계에 대해 다음과 같은 근사한 항등식을 사용하는 경우:
요람 ( x ) = ∑ n = − ∞ ∞ 1 2 π n + 2 x − 1 2 π n − 2 x \displaystyle \cot(x)=\sum _{n=-\infty}^{\infty}{\frac {1}{2\pi n+2x}-{\frac {1}{2\pi n-2x}}}} 그리고 그것을 우리의 표현에 연결하면 다음과 같은 결과를 얻을 수 있습니다. ℏ 2 2 m a A = − a 4 α [ 요람 ( k a 2 − α a 2 ) − 요람 ( k a 2 + α a 2 ) ] {\displaystyle {\frac ^{2}} {2m} {\frac {a} { A}}=-{\frac {a}{4\alpha}}\left[\cot \left\tfrac {ka}{2}-\cot \tfrac {ka}{2}+{\tfrac {\alpha}{}\right}
요람 의 합계를 사용한 후, sin 의 곱(요람 의 합계에 대한 공식의 일부)은 다음과 같습니다.
왜냐하면 ( k a ) = 왜냐하면 ( α a ) + m A ℏ 2 α 죄 ( α a ) \displaystyle \cos(ka)=\cos(\alpha a)+{\frac {m} A}{\hbar^{2}\alpha}}\sin(\alpha a)}
이 방정식은 에너지(α를 통해 )와 파동 벡터, k 의 관계를 나타내며, 보다시피 방정식의 왼쪽은 -1 에서 1 까지밖에 되지 않기 때문에 α(그리고 에너지)가 취할 수 있는 값에는 한계가 있습니다. 즉, 에너지 값의 일부 범위에서는 이러한 등식에 따른 해답은 없습니다. 따라서 시스템은 에너지 격차라는 에너지를 갖지 않습니다. 이른바 밴드갭(band-gaps)으로, (델타 장벽이나 사각 장벽뿐만 아니라) 모든 형태의 주기적 전위(portial potential)로 존재할 수 있습니다.
갭 공식(즉 밴드 간 간격)과 1차원 슈뢰딩거 방정식의 고유값 수준 분할에 대한 다르고 상세한 계산은 뮐러-커스틴을 [4] 코사인 퍼텐셜(마티외 방정식)에 대한 대응 결과도 이 참조에서 자세히 제시된다.
「 」를 참조해 주세요. 레퍼런스 ^ Bloch, Felix (1929). "Über die Quantenmechanik der Elektronen in Kristallgittern". Zeitschrift für Physik (in German). Springer Science and Business Media LLC. 52 (7–8): 555–600. doi :10.1007/bf01339455 . ISSN 1434-6001 . ^ de L. Kronig, R.; Penney, W. G. (3 February 1931). "Quantum Mechanics of Electrons in Crystal Lattices" . Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences . The Royal Society. 130 (814): 499–513. doi :10.1098/rspa.1931.0019 ISSN 1364-5021 . ^ Surjit Singh (1983). "Kronig–Penney model in reciprocal lattice space". American Journal of Physics . 51 : 179. doi :10.1119/1.13321 . ^ Harald J. W. Muller-Kirsten, 양자역학 입문: 슈뢰딩거 방정식과 경로 적분, 제2판, 세계과학(싱가포르, 2012), 325–329, 458–477.
외부 링크 
 갖는 블로흐 인자이며, 크로니그-페니 전위 또는 마티외 방정식과 같은 코사인 함수로 슈뢰딩거 방정식의 에너지 스펙트럼 밴드 구조를 발생시킨다.
갖는 블로흐 인자이며, 크로니그-페니 전위 또는 마티외 방정식과 같은 코사인 함수로 슈뢰딩거 방정식의 에너지 스펙트럼 밴드 구조를 발생시킨다. 












![{\displaystyle \cos(ka)=\cos(\beta b)\cos[\alpha (a-b)]-{\alpha ^{2}+\beta ^{2} \over 2\alpha \beta }\sin(\beta b)\sin[\alpha (a-b)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74a8b0edda1c93ea56f8115118f44cce119f6d46)




![{\displaystyle \cos(ka)=\cos(\beta b)\cosh[\alpha (a-b)]-{\beta ^{2}-\alpha ^{2} \over 2\alpha \beta }\sin(\beta b)\sinh[\alpha (a-b)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8681005213939d2b1c51fbe32f46f5694915d18)






 나타냅니다
나타냅니다
 취하여 k를 계산할 수 있다.따라서 이 표현은
취하여 k를 계산할 수 있다.따라서 이 표현은 







![{\displaystyle \left[{\frac {\hbar ^{2}(k+K)^{2}}{2m}}-E_{k}\right]{\tilde {u}}_{k}(K)+\sum _{K'}{\tilde {V}}(K-K')\,{\tilde {u}}_{k}(K')=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f4f33b6febe283e9b65645db5de95635fe6b3a1)
![{\displaystyle \left[{\frac {\hbar ^{2}(k+K)^{2}}{2m}}-E_{k}\right]{\tilde {u}}_{k}(K)+{\frac {A}{a}}\sum _{K'}{\tilde {u}}_{k}(K')=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/078d42c383c7869a198076af85e2367223058fcc)

![{\displaystyle \left[{\frac {\hbar ^{2}(k+K)^{2}}{2m}}-E_{k}\right]{\tilde {u}}_{k}(K)+{\frac {A}{a}}u_{k}(0)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37c9feaabaf61a84c71b3395049f24e790e02472)




 (가) 취소되고 다음과 같이 표시됩니다.
(가) 취소되고 다음과 같이 표시됩니다.





![{\displaystyle {\begin{aligned}{\frac {\hbar ^{2}}{2m}}{\frac {a}{A}}&=\sum _{n=-\infty }^{\infty }{\frac {1}{\alpha ^{2}-(k+{\frac {2\pi n}{a}})^{2}}}\\&=-{\frac {1}{2\alpha }}\sum _{n=-\infty }^{\infty }\left[{\frac {1}{(k+{\frac {2\pi n}{a}})-\alpha }}-{\frac {1}{(k+{\frac {2\pi n}{a}})+\alpha }}\right]\\&=-{\frac {a}{4\alpha }}\sum _{n=-\infty }^{\infty }\left[{\frac {1}{\pi n+{\frac {ka}{2}}-{\frac {\alpha a}{2}}}}-{\frac {1}{\pi n+{\frac {ka}{2}}+{\frac {\alpha a}{2}}}}\right]\\&=-{\frac {a}{4\alpha }}\left[\sum _{n=-\infty }^{\infty }{\frac {1}{\pi n+{\frac {ka}{2}}-{\frac {\alpha a}{2}}}}-\sum _{n=-\infty }^{\infty }{\frac {1}{\pi n+{\frac {ka}{2}}+{\frac {\alpha a}{2}}}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6ba6686b2b4340398c82c27c2b16cd7906a8b10)

![{\displaystyle {\frac {\hbar ^{2}}{2m}}{\frac {a}{A}}=-{\frac {a}{4\alpha }}\left[\cot \left({\tfrac {ka}{2}}-{\tfrac {\alpha a}{2}}\right)-\cot \left({\tfrac {ka}{2}}+{\tfrac {\alpha a}{2}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f10a349eb587ba574a1a75c0d3b22d3bd803ab2)



