빈 격자 근사치

전자 구조 방법
발란스 본드 이론
콜슨-피셔 이론 일반화 발란스 본드 모던발란스 본드
분자 궤도 이론
하트리-포크 방식 반감기 양자화학법 뫼르-플레셋 섭동 이론 구성 상호 작용 커플링 클러스터 다중 구성 자체 일관성 필드 양자화학복합법 퀀텀 몬테 카를로
밀도함수이론
시간 의존적 밀도 기능 이론 토마스-페르미 모델 궤도무밀도기능이론
전자 밴드 구조
거의 자유 전자 모델 타이트 바인딩 머핀틴 근사치 k·p 섭동설 빈 격자 근사치
v t

빈 격자 근사치는 전위가 주기적이고 약한 이론적인 전자 밴드 구조 모델이다(상수에 가깝다).또한^{[clarification needed]} 전위가 주기적이지도 않은 빈 불규칙 격자를 고려할 수 있다.^[1]빈 격자 근사치는 결정 격자를 통해 이동하는 비 상호 작용 자유 전자의 에너지 분산 관계의 여러 특성을 설명한다."빈 격자"에 있는 전자의 에너지는 자유 전자의 에너지와 같다.이 모델은 모든 전자 밴드 구조에 기초하는 고형물에서 에너지 분산 관계의 때때로 매우 복잡한 특징들을 명확하게 설명하기 때문에 유용하다.null

산란 및 주기성

이 자유 전자 모델에서 격자의 주기적 전위는 약해야 한다. 그렇지 않으면 전자가 자유롭지 못할 것이기 때문이다.산란 강도는 주로 시스템의 기하학적 구조와 위상에 따라 결정된다.단면 산란과 같이 국소적으로 정의된 매개변수는 전위의 크기와 전위의 크기에 따라 달라진다.1차원, 2차원 및 3차원 공간의 경우, 잠재력이 아무리 작더라도, 징후가 무엇이고 크기가 얼마나 제한되어 있든 간에 항상 파동을 산란시킨다.크로니그-페니 모델과 같이 1차원 격자 내 입자의 경우, 전위, 격자 간격 및 전위 유정 크기에 대한 값을 대체하여 밴드 구조를 분석적으로 계산할 수 있다.^[2]2차원 문제와 3차원 문제의 경우 몇 개의 매개변수를 가진 유사한 모델을 바탕으로 밴드 구조를 계산하는 것이 더 어렵다.그럼에도 불구하고, 밴드 구조의 특성은 섭동 방법에 의해 대부분의 지역에서 쉽게 근사치할 수 있다.null

이론적으로 격자는 무한히 크기 때문에, 약한 주기적 산란 전위는 결국 파동을 반영할 수 있을 정도로 강해질 것이다.산란 과정은 결정 구조의 주기적 전위에 의해 잘 알려진 Bragg 반사의 결과를 낳는다.이것이 브릴루인 구역에서 분산관계의 주기성과 k-공간 분할의 기원이다.주기적인 에너지 분산 관계는 다음과 같이 표현된다.

${\displaystyle E_{n}(\mathbf {k})={\frac {\hbar ^{2}(\mathbf {k} +\mathbf {g} _{n}^{2m}}}}}}}}$

$G{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$은^{[clarification needed]}(는) 대역 ${\displaystyle {En}_{}}$ (${\displaystyle {}_{}}$k${\displaystyle }$) ${\displaystyle E_{n}(\mathbf {k}$ )이$($가) 속하는 상호$$ 격자 벡터다$$.null

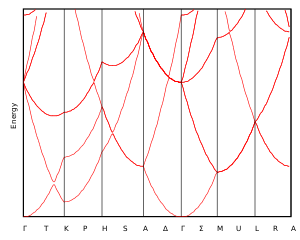
오른쪽 그림은 길이 a의 격자 세포를 가진 1차원 격자의 상호적 공간에서 세 기간의 분산 관계를 보여준다.

에너지 대역과 상태 밀도

1차원 격자에서 에너지 간격에서 대역을 결정하는$$ 상호 격자 벡터 ${\displaystyle {}_{}}$ $n{\displaystyle {\mathbf{}}_{}}$ ${\$의 수는 에너지가 상승할 때 2로 제한된다.2차원 및 ${\displaystyle 3차원\mathbf{}}$ 격자에서 자유 전자 대역 ${\displaystyle {En}_{}}$( k$){\displaystyle E_{n}(\mathbf {k}$)을 결정하는 상호 격자 벡터의 수는 파장 벡터의 길이가 증가하고 에너지가 상승할 때 더 빠르게 증가한다$$.이는${\displaystyle }$[${\displaystyle k\mathbf{},}$ ${\displaystyle k}$+ ${\displaystyle d\mathbf{}}$ $]{\daystyle$$\mathbf{G} _{n}]$ 간격으로 놓여 있는$$ 상호 격자 벡터 $G{\displaystyle {\mathbf{}}_{}}$ ${\$ \mathbf {$k},\mathbf {k} +d\mathbf {k} ]$의 수가$$ 증가하기 때문이다.The density of states in an energy interval ${\displaystyle [E,E+dE]}$ depends on the number of states in an interval ${\displaystyle [\mathbf {k} ,\mathbf {k} +d\mathbf {k} ]}$ in reciprocal space and the slope of the dispersion relation ${\displaystyle E_{n}(\mathbf {k} )}$.

격자 셀이 연속적으로 대칭되는 것은 아니지만, 산포 관계가 중심 브릴루인 영역 밖으로 확장되는 경우, 역수 격자 셀의 고정된 중심 지점의 관점에서 볼 때 여전히 구형 대칭이 있다.3차원 격자 안의 상태 밀도는 격자가 없는 경우와 동일할 것이다.3차원 사례의 경우 상태 $D{\displaystyle {}_{}}$ ${\displaystyle {3\mathrm{}}_{}}$( ${\displaystyle E}$) ${\$의 밀도는 다음과 같다$$.

${\displaystyle D_{3}\왼쪽(E\오른쪽)=2\pi {\sqrt {\frac {E-E_{0}}{c_{k}^{3}}\ .}$

3차원 공간에서 브릴루인 구역 경계는 평면이다.분산 관계는 가능한 모든 상호 격자 벡터에 대한 자유 전자 에너지 분산 포물선의 원리를 보여준다.이는 평가 궤적, 1차 및 상위 순서 브릴루인 구역 경계, 분산 포물선 교차 원뿔 사이에 가능한 각도가 많기 때문에 분산 관계를 계산할 때 곡선의 교차로를 매우 복잡하게 설정하게 된다.null

두 번째, 세 번째 및 더 높은 브릴루인 구역

제1차 브릴루인 존 바깥 먼$$ 곳까지 파장 $벡터{\displaystyle \mathbf{}}$ k ${\$이(가) 있는 고체의 격자를 통해 이동하는 "자유 전자"는 여전히 제1차 브릴루인 존에 다시 반사된다.예제 및 그림이 있는 사이트는 외부 링크 섹션을 참조하십시오.null

거의 자유로운 전자 모델

알루미늄과 같은 대부분의 단순한 금속에서 스크리닝 효과는 고체에 있는 이온의 전기장을 강하게 감소시킨다.정전기 전위는 다음과 같이 표현된다.

${\displaystyle V(r)={\frac {Ze}{r}e^{-qr}}}$

여기서 Z는 원자 번호, e는 기본 단위 전하, r은 내장 이온의 핵까지의 거리, q는 전위의 범위를 결정하는 선별 파라미터다.격자전위 $V{\displaystyle }$($$$){\displaystyle U_$${\mathbf$${G}}}}}$의 ${\displaystyle {Fourier\mathbf{}}_{}}$ $변환$은 다음과 같이 표현된다$.$

${\displaystyle U_{\mathbf {G}}={\frac {4\pi Ze}{q^{2}+G^{2}}:$

해밀턴의 상호 격자 벡터 사이의 비대각$$ 원소 $U{\displaystyle {}_{}}$ ${\displaystyle {G\mathbf{}}_{}}$ ${\$의 값이 거의 0으로 갈 때.그 결과 밴드 갭 $2{\displaystyle \mathrm{}}$ ${\displaystyle U{}_{}}$ ${\displaystyle {G\mathbf{}}_{}}$ $displaystyle$2$U_{\mathbf {G}}}}$의 크기가 붕괴되고 빈 격자 근사치가 얻어진다.null

일반 금속 결정의 전자 밴드

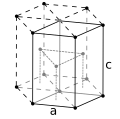
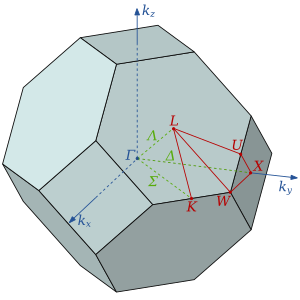
몇 가지 이국적인 예외를 제외하고 금속은 BCC 및 FCC 입방 결정 구조와 육각형 근접 포장 HCP 결정 구조라는 세 가지 종류의 결정 구조로 결정된다.null

• 

  체중심입방체(I)

• 

  얼굴 중심 큐빅(F)

• 

  육각형 근접포장

참조

외부 링크

• Tayer Watkins의 Brielouin Zone 단순 격자 도표
• 테크니온의 브릴루인존 3d 격자 도표.
• DoITPoMS 교육 및 학습 패키지 - "Brillouin Zones"