유한 구면 대칭군 목록

List of finite spherical symmetry groups
3차원의 점 그룹
Sphere symmetry group cs.png
비자발적 대칭
Cs, (*)
[ ] = CDel node c2.png 		Sphere symmetry group c3v.png
순환 대칭
Cnv, (*n)
[n] = CDel node c1.pngCDel n.pngCDel node c1.png 		Sphere symmetry group d3h.png
치측 대칭
Dnh, (*n22)
[n,2] = CDel node c1.pngCDel n.pngCDel node c1.pngCDel 2.pngCDel node c1.png
다면군, [n,3], (*n32)
Sphere symmetry group td.png
사면 대칭
Td, (*332)
[3,3] = CDel node c1.pngCDel 3.pngCDel node c1.pngCDel 3.pngCDel node c1.png 		Sphere symmetry group oh.png
팔면 대칭
Oh, (*432)
[4,3] = CDel node c2.pngCDel 4.pngCDel node c1.pngCDel 3.pngCDel node c1.png 		Sphere symmetry group ih.png
이코사면 대칭
Ih, (*532)
[5,3] = CDel node c2.pngCDel 5.pngCDel node c2.pngCDel 3.pngCDel node c2.png

유한 구면 대칭 그룹은 3차원으로 점군이라고도 한다.삼각형의 기본 영역을 갖는 5가지 기본 대칭 등급이 있다: 이음, 주기, 사음부, 팔면부, 이음부 대칭이다.

이 글은 쇤파리 표기법, 콕시터 표기법,[1] 오비폴드 표기법,[2] 순서별로 집단을 나열한다.존 콘웨이는 그룹의 쿼터니온 대수적 구조와 대문자 한두 개와 정수 첨자로 라벨을 붙인 쇤파리 표기법의 변형을 사용한다.그룹 순서는 중앙 역전을 의미하는 + 또는 마이너스, "±" 접두사를 가진 기호에 대해 순서가 두 배가 되지 않는 한 첨자로 정의된다.[3]

헤르만-마우긴 표기법(국제 표기법)도 주어진다.결정학 그룹은 총 32개로 원소 순서 2, 3, 4, 6이 있는 부분집합이다.[4]

비자발적 대칭

비자발적 집단은 대칭 없음(C1), 반사 대칭(Cs), 2배 회전 대칭(C2), 중앙점 대칭(Ci) 등 4개다.

인틀 지오
 오비폴드 쇤플라이스 콘웨이 콕시터 주문 추상적 자금을 마련하다.
도메인
1 1 11 C1 C1 ][
[ ]+ 		1 Z1 Sphere symmetry group c1.png
2 2 22 D1
= C2 		D2
= C2 		[2]+ 2 Z2 Sphere symmetry group c2.png
1 22 × Ci
= S2 		CC2 [2+,2+] 2 Z2 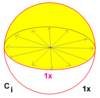Sphere symmetry group ci.png
2
= m		 1 * Cs
= C1v
= C1h 		±C1
= CD2 		[ ] 2 Z2 Sphere symmetry group cs.png

순환 대칭

4개의 무한순환 대칭 패밀리가 있으며, n = 2 이상이다. (n은 대칭이 없는 특수한 경우 1일 수 있음)

인틀 지오
 오비폴드 쇤플라이스 콘웨이 콕시터 주문 추상적 자금을 마련하다.
도메인
4 42 2× S4 CC4 [2+,4+] 4 Z4 Sphere symmetry group s4.png
2/m 22 2* C2h
= D1d 		±C2
= ±D2 		[2,2+]
[2+,2]		 4 Z4 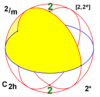Sphere symmetry group c2h.png
인틀 지오
 오비폴드 쇤플라이스 콘웨이 콕시터 주문 추상적 자금을 마련하다.
도메인
2
3
4
5
6
n 		2
3
4
5
6
n 		22
33
44
55
66
nn		 C2
C3
C4
C5
C6
Cn 		C2
C3
C4
C5
C6
Cn 		[2]+
[3]+
[4]+
[5]+
[6]+
[n]+
 2
3
4
5
6
n 		Z2
Z3
Z4
Z5
Z6
Zn 		Sphere symmetry group c2.png
2mm
3m
4mm
5m
6mm
nm(n은 홀수)
nmm(n이 짝수)		 2
3
4
5
6
n 		*22
*33
*44
*55
*66
*nn		 C2v
C3v
C4v
C5v
C6v
Cnv 		CD4
CD6
CD8
CD10
CD12
CD2n 		[2]
[3]
[4]
[5]
[6]
[n]		 4
6
8
10
12
2n		 D4
D6
D8
D10
D12
D2n 		Sphere symmetry group c2v.png
3
8
5
12
-		 62
82
10.2
12.2
2n.2 		3×
4×
5×
6×
n×		 S6
S8
S10
S12
S2n 		±C3
CC8
±C5
CC12
CC2n / ±Cn 		[2+,6+]
[2+,8+]
[2+,10+]
[2+,12+]
[2+,2n+]		 6
8
10
12
2n		 Z6
Z8
Z10
Z12
Z2n 		Sphere symmetry group s6.png
3/m=6
4/m
5/m=10
6/m
n/m		 32
42
52
62
n2		 3*
4*
5*
6*
n*		 C3h
C4h
C5h
C6h
Cnh 		CC6
±C4
CC10
±C6
±Cn / CC2n 		[2,3+]
[2,4+]
[2,5+]
[2,6+]
[2,n+]		 6
8
10
12
2n		 Z6
Z2×Z4
Z10
Z2×Z6
Z2×Zn
≅Z2n(이상 n)		 Sphere symmetry group c3h.png

치측 대칭

3개의 무한 이면 대칭 패밀리가 있으며, n = 2 이상이다(n은 특수한 경우 1일 수 있다).

인틀 지오
 오비폴드 쇤플라이스 콘웨이 콕시터 주문 추상적 자금을 마련하다.
도메인
222 2.2 222 D2 D4 [2,2]+ 4 D4 Sphere symmetry group d2.png
42m 42 2*2 D2d DD8 [2+,4] 8 D4 Sphere symmetry group d2d.png
음. 22 *222 D2h ±D4 [2,2] 8 Z2×D4 Sphere symmetry group d2h.png
인틀 지오
 오비폴드 쇤플라이스 콘웨이 콕시터 주문 추상적 자금을 마련하다.
도메인
32
422
52
622 		3.2
4.2
5.2
6.2
N.2 		223
224
225
226
22n		 D3
D4
D5
D6
Dn 		D6
D8
D10
D12
D2n 		[2,3]+
[2,4]+
[2,5]+
[2,6]+
[2,n]+ 		6
8
10
12
2n 		D6
D8
D10
D12
D2n 	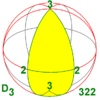	Sphere symmetry group d3.png
3m
82m
5m
12.2m
 62
82
10.2
12.2
n2
 2*3
2*4
2*5
2*6
2*n		 D3d
D4d
D5d
D6d
Dnd 		±D6
DD16
±D10
DD24
DD4n / ±D2n 		[2+,6]
[2+,8]
[2+,10]
[2+,12]
[2+,2n]		 12
16
20
24
4n		 D12
D16
D20
D24
D4n 		Sphere symmetry group d3d.png
6㎡
4/10
10㎡
6/10		 32
42
52
62
n2		 *223
*224
*225
*226
*22n		 D3h
D4h
D5h
D6h
Dnh 		DD12
±D8
DD20
±D12
±D2n / DD4n 		[2,3]
[2,4]
[2,5]
[2,6]
[2,n]		 12
16
20
24
4n		 D12
Z2×D8
D20
Z2×D12
Z2×D2n
≅D4n(이상 n)		 Sphere symmetry group d3h.png

다면 대칭

추가 정보:다면군

다면 대칭에는 세 가지 유형이 있는데, 사면 대칭, 팔면 대칭, 이 대칭과 함께 삼각형 면의 정규 다면 대칭의 이름을 딴 것이다.

사면 대칭
인틀 지오
 오비폴드 쇤플라이스 콘웨이 콕시터 주문 추상적 자금을 마련하다.
도메인
23 3.3 332 T T [3,3]+
= [4,3+]+ 		12 A을4 Sphere symmetry group t.png
m3 43 3*2 Th ±T [4,3+] 24 2×A4 Sphere symmetry group th.png
43m 33 *332 Td 토 [3,3]
= [1+,4,3]		 24 S4 Sphere symmetry group td.png
팔면 대칭
인틀 지오
 오비폴드 쇤플라이스 콘웨이 콕시터 주문 추상적 자금을 마련하다.
도메인
432 4.3 432 O O [4,3]+
= [[3,3]]+ 		24 S4 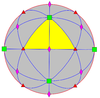Sphere symmetry group o.png
m3m 43 *432 Oh ±O [4,3]
= [[3,3]]		 48 2×S4 Sphere symmetry group oh.png
이코사면 대칭
인틀 지오
 오비폴드 쇤플라이스 콘웨이 콕시터 주문 추상적 자금을 마련하다.
도메인
532 5.3 532 I I [5,3]+ 60 A을5 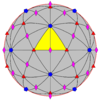Sphere symmetry group i.png
532/m 53 *532 Ih ±I [5,3] 120 2×A5 Sphere symmetry group ih.png

참고 항목

참조

  1. ^ 존슨, 2015년
  2. ^ Conway, John H. (2008). The symmetries of things. Wellesley, Mass: A.K. Peters. ISBN 978-1-56881-220-5. OCLC 181862605.
  3. ^ Conway, John; Smith, Derek A. (2003). On quaternions and octonions: their geometry, arithmetic, and symmetry. Natick, Mass: A.K. Peters. ISBN 978-1-56881-134-5. OCLC 560284450.
  4. ^ 샌즈, 1993년

추가 읽기

  • 피터 R.크롬웰, 폴리헤드라(1997), 부록 I
  • Sands, Donald E. (1993). "Crystal Systems and Geometry". Introduction to Crystallography. Mineola, New York: Dover Publications, Inc. p. 165. ISBN 0-486-67839-3.
  • 2003년 Quaternions와 Octonion에서는 John Horton Conway와 Derek A.스미스 ISBN 978-1-56881-134-5
  • The Symmetries of Things 2008, John H. Conway, Hidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5
  • 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6[1]
    • (용지 22) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 I, [산술]Zeit. 46 (1940) 380–407, MR 2,10]
    • (용지 23) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, [수학]Zeit. 188 (1985) 559–591]
    • (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술]Zeit. 200 (1988) 3–45]
  • N.W. Johnson: 기하학과 변환, (2018) ISBN 978-1-107-10340-5 제11장: 유한대칭군, 표 11.4 3-공간에서의 이소메트리 유한군

외부 링크