마그너스 효과

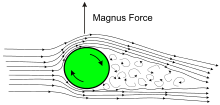
마그너스 효과는 유체를 통해 움직이는 회전 물체와 일반적으로 연관되는 관측 가능한 현상이다. 회전하는 물체의 경로는 물체가 회전하지 않을 때 존재하지 않는 방식으로 꺾인다. 편향은 회전하는 물체의 반대편에 있는 액체의 압력 차이로 설명될 수 있다. 마그너스 효과는 회전 속도에 따라 달라진다.

마그너스 효과의 가장 쉽게 관찰할 수 있는 경우는 회전하는 구(또는 실린더)가 회전하지 않으면 따라올 호로부터 휘어지게 되는 경우다. 축구와 배구 선수, 야구 투수, 크리켓 볼링 선수 등이 자주 사용한다. 결과적으로, 이 현상은 많은 구기 종목의 물리학 연구에서 중요하다. 또한 회전이 유도 미사일에 미치는 영향을 연구하는 데 중요한 요인이며, 예를 들어 회전자 선박과 플레트너 항공기의 설계와 같은 공학적 용도가 있다.

볼 게임에서 톱스핀은 이동 방향으로 볼의 상단 표면을 움직이는 이동 방향에 수직인 수평 축을 중심으로 회전하는 것으로 정의된다. 마그너스 효과에 따르면 톱스핀은 중력만으로 만들어질 수 있는 것보다 더 큰, 움직이는 공의 아래쪽으로 휙 방향을 바꾼다. 백스핀은 움직이는 공의 비행을 연장시키는 위력을 만들어낸다.^[1] 마찬가지로 사이드 스핀은 슬라이더와 같은 일부 야구 경기 중 어느 쪽으로든 방향을 틀게 한다.^[2] 전체적인 거동은 에어로포일 주위의 거동과 유사하지만(양력 참조), 에어포일 작용보다는 기계적 회전에 의해 발생하는 순환이 있다.^[3]

마그누스 효과는 이를 조사한 독일의 물리학자 하인리히 구스타프 마그누스의 이름을 따서 지은 것이다. 회전 실린더에 가해지는 힘은 그 효과를 처음 분석한 마틴 쿠타와 니콜라이 주코프스키(또는 주코프스키)의 뒤를 이어 쿠타-주코프스키 리프트로 알려져 있다.^[4]

물리학

이 현상에 대한 직관적인 이해는 신체에 대한 굴절력이 신체가 공기 흐름에 부과하는 굴절에 대한 반응이라는 뉴턴의 제3법칙에서 나온다. 몸은 공기를 한 방향으로 '밀고' 공기는 다른 방향으로 몸을 밀어낸다. 특히 공기 흐름의 하향 편향과 함께 리프팅 힘이 동반된다. 그것은 신체의 뒤쪽에 있는 유체 흐름에서 각도가 변형된 것이다.

라이먼 브릭스(Lyman Briggs^[5])가 야구계에 미치는 마그누스 효과에 대해 풍동 연구를 했고, 그 효과에 대한 이미지를 제작한 사람들도 있다.^[5][6][7][8] 연구결과에 따르면 회전공 뒤쪽에서 난기류가 일어나면 공기역학적 드래그가 발생하며, 그 외에도 그 후각에는 눈에 띄는 각도가 있으며, 이러한 편향은 스핀의 방향에 있다.

기류에서 난기류가 몸 뒤에서 일어나는 과정은 복잡하지만 공기역학에서는 잘 연구되고 있다. 얇은 경계층은 어느 순간 신체로부터 스스로를 분리시켜("흐름 분리")하며, 여기서부터 경각심이 발달하기 시작한다. 경계층 자체가 난동할 수도 있고 그렇지 않을 수도 있으며, 그것은 웨이크 형성에 상당한 영향을 미친다. 신체의 표면 조건의 상당히 작은 변화는 웨이크 형성의 시작에 영향을 미칠 수 있으며, 따라서 하류 흐름 패턴에 현저한 영향을 미칠 수 있다. 몸의 회전이 미치는 영향은 이와 같다.

마그너스 자신이 마그너스 효과의 원인으로 피부 마찰과 점성 때문에 층류로 이론적 효과를 잘못 가정했다고 한다. 그러한 효과는 물리적으로는 가능하지만 마그누스 효과에서 적절한 효과를 내는 것에 비하면 미미하다.^[5] 어떤 상황에서는 마그너스 효과의 원인이 마그너스 효과의 그것과 반대되는 변형을 만들 수 있다.^[8]

위의 도표는 뒷바퀴 돌기 공에서 생산되는 양력을 보여준다. 웨이크업과 후행 기류가 아래로 꺾였다. 경계층 운동은 공 표면의 회전 운동이 전진하는 공의 하부에서 더욱 격렬하게 전개되며 공의 번역 운동 효과를 강화한다. 경계층은 짧은 간격 후에 난기류를 발생시킨다.

야구에서 이 효과는 야구가 앞으로 회전하는 커브볼의 하향 움직임을 유발하는 데 사용된다('톱스핀'으로). 다른 종목의 참가자들도 공을 가지고 노는 것은 이러한 효과를 이용하는 것이다.

실린더에서 회전에 의한 힘을 쿠타-쥬코스키 리프트라고 한다. 회전에 의해 생성된 소용돌이의 관점에서 분석할 수 있다. 실린더의 단위 길이당 리프트.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output .sfra.그 속도의 C.den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}F/L, 제품은, v(초당미터 달리기에서), 그 액체,ρ(kg/m3에)의 밀도, 그리고 회전에 의해 성립되던 와중의 힘 G:[4].

${\displaystyle {\frac {F}{L}=\rho vG,}$

에 의해 소용돌이 강도가 주어지는 곳

${\displaystyle G=(2\pi r)^{2}s=2\pi r^{2}\omega ,}$

여기서 s는 실린더의 회전(초당 회전수), Ω은 실린더의 회전각 속도(라디안/초 단위), r은 실린더의 반지름(미터 단위)이다.

역사

독일의 물리학자 하인리히 구스타프 마그누스는 1852년에 그 효과를 설명했다.^[9][10] 그러나 1672년 아이작 뉴턴은 그것을 설명하고 캠브리지 대학에서 테니스 선수들을 관찰한 후 그 원인을 정확하게 추론했다.^[11][12] 1742년 영국의 수학자, 탄도 연구자, 군사 기술자인 벤자민 로빈스는 머스킷볼의 궤적에서의 편차를 마그누스 효과의 관점에서 설명했다.^{[13][14][15][16]}

스포츠로

마그너스 효과는 스포츠에서 회전하는 공의 일반적인 궤적이나 경로, 특히 축구, 탁구,^[17] 테니스,^[18] 배구, 골프, 야구, 크리켓에서 흔히 관찰되는 편차를 설명한다.

슬라이스나 후크라고 알려진 골프공의 굽은 경로는 공이 회전하는 운동(수직축에 대하여)과 마그너스 효과로 인해 공이 궤적에서 직선으로 움직이는 수평력이 크게 작용한다.^{[19]: § 4.5} 골프공 위의 백스핀(이동 방향에서 뒤로 회전하는 표면)은 중력의 힘을 약간 상쇄시키는 수직력을 유발하며, 공이 회전하지 않았을 때보다 조금 더 오랫동안 공중에 떠 있을 수 있게 한다: 이것은 공이 수평 축을 중심으로 회전하지 않는 공보다 더 멀리 이동할 수 있게 한다..^{[citation needed]}

탁구에서는 볼의 질량이 작고 밀도가 낮기 때문에 마그너스 효과를 쉽게 관찰할 수 있다. 경험이 많은 선수는 다양한 스핀을 볼에 배치할 수 있다. 탁구 라켓은 보통 라켓이 공을 최대한 쥐게 하기 위해 고무로 만들어진 표면을 가지고 있다.

마그너스 효과는 '말링가 스윙'^[20][21]의 원인이 될 수 있고, 스핀 볼링의 드리프트와 딥이라고 알려진 동작에 기여하지만,^{[19]: Fig. 4.19} 기존의 스윙 볼링에서 볼 수 있는 크리켓 볼링의 움직임에 대해서는 책임이 없다.

에어소프트에서는 골프와 비슷한 방식으로 마그너스 효과를 사용해 홉업(홉업)으로 알려진 시스템을 사용해 사거리를 크게 늘린 BB에 백스핀을 만든다.

야구에서는 투수들이 서로 다른 스핀을 공에 전달하는 경우가 많아 마그너스 효과로 인해 원하는 방향으로 커브를 돌게 된다. 피치프/x 시스템은 메이저리그에서 던지는 모든 투구에서의 매그너스에 의한 궤도 변화를 측정한다.^[22]

2010년 FIFA 월드컵 매치볼은 이전 매치볼과는 다른 마그누스 효과로 비판을 받아왔다. 그 공은 마그누스 효과가 적고 그 결과 멀리 날아갈 수 있지만 제어 가능한 스윕이 적은 것으로 설명되었다.^[23]

외부 탄도학에서

마그너스 효과는 고급 외부 탄도학에서도 찾아볼 수 있다. 첫째, 비행중 회전탄은 좌우 어느 한쪽에서 불어오는 것으로 단순화할 수 있는 역풍을 동반하는 경우가 많다. 게다가, 완전히 차분한 공기에서도 총알은 좌우운동으로 인해 작은 옆바람 구성요소를 경험한다. 총알의 비행 경로를 따라 움직이는 이 요 동작은 총알의 코가 총알이 이동하는 방향과 약간 다른 방향을 가리키고 있다는 것을 의미한다. 즉, 총알은 주어진 순간에 옆으로 "스키드"하여 어떤 옆바람 요소 외에 작은 옆바람 요소도 경험하게 된다.^[24]

이 두 효과의 결합된 측면 바람 요소는 탄환에 마그누스 힘이 작용하게 하는데, 탄환이 가리키는 방향과 결합된 측면 바람 모두에 수직이다. 우리가 여러 가지 복잡한 요인을 무시하는 아주 간단한 경우, 옆바람으로부터 오는 마그누스 힘이 회전탄에 대해 위아래로 작용하게 되어(좌우 또는 우풍과 회전에 따라 달라짐) 탄환의 비행 경로가 위아래로 편향되어 충격 지점에 영향을 미치게 된다.

전반적으로 총알의 비행 경로 자체에 대한 마그너스 힘의 영향은 공기역학 드래그와 같은 다른 힘에 비해 보통 미미하다. 하지만, 그것은 탄환의 안정성에 큰 영향을 미치고, 탄환이 드래그의 양, 충격에 의해 어떻게 행동하는지, 그리고 다른 많은 요소들에 영향을 미친다. 총알의 안정성은 영향을 받는다. 왜냐하면 마그누스 효과는 총알의 무게중심이 아니라 탄환의 압력중심에 작용하기 때문이다.^[25] 이는 탄환의 요 각도에 영향을 미친다는 것을 의미한다. 탄환은 비행 축을 향해 또는 비행 축에서 멀리 떨어져서(요를 감소시켜 탄환을 안정화함) 비행 경로를 따라 탄환을 비틀려는 경향이 있다. 결정적인 요인은 유량장 구조에 따라 좌우되는 압력 중심부의 위치인데, 이는 주로 탄환 속도(초음파 또는 아음파)에 따라 달라지지만 모양, 공기 밀도, 표면 특징에도 좌우된다. 압력 중심이 무게 중심보다 앞에 있으면 효과가 불안정하고, 압력 중심이 무게 중심보다 뒤에 있으면 효과가 안정화되고 있다.^[26]

항공분야에서

일부 항공기는 마그너스 효과를 이용해 날개 대신 회전 실린더로 리프트를 만들어 낮은 수평 속도로 비행할 수 있도록 제작됐다.^[4] 마그누스 효과를 공중보다 무거운 비행기에 사용하려는 가장 초기 시도는 1910년 매사추세츠 주의 버틀러 아메스에 의한 것이었다. 다음 시도는 1930년대 초 뉴욕 주의 세 발명가에 의한 것이었다.^[27]

선박추진 및 안정화

로터 배들은 추진력을 위해 Flettner 로터라고 불리는 돛대 모양의 실린더를 사용한다. 이것들은 배의 갑판에 수직으로 탑재되어 있다. 옆에서 바람이 불면 마그너스 효과가 앞으로 추력을 일으킨다. 따라서 여느 범선과 마찬가지로 회전선은 바람이 불어야만 전진할 수 있다. 이 효과는 또한 수선 아래에 장착된 회전 실린더와 횡방향으로 나타나는 특수 유형의 선박 스태빌라이저에도 사용된다. 회전 방향과 속도를 조절해 강한 리프트나 다운포스(downforce)를 발생시킬 수 있다.^[28] 현재까지 이 시스템의 가장 큰 배치는 모터 요트 이클립스에 있다.

참고 항목

• 공기저항
• 세기의 공
• 베르누이의 원리
• 코안데르 효과
• 유체 역학
• 연형
• 나비에-스토크스 방정식
• 레이놀즈 수
• 테슬라 터빈

참조

추가 읽기

• Watts, R. G. & Ferrer, R. (1987). "The lateral force on a spinning sphere: Aerodynamics of a curveball". American Journal of Physics. 55 (1): 40. Bibcode:1987AmJPh..55...40W. doi:10.1119/1.14969.

외부 링크

위키미디어 커먼즈에는 매그너스 효과와 관련된 미디어가 있다.

• Magnus Cups, Ri Channel 비디오, 2012년 1월
• 수학 페이지의 분석 기능, 매그너스 효과 및 윙
• 총알은 어떻게 날아갈까? 독일 비스바덴의 뤼프레히트 넨스티엘
• 총알은 어떻게 날까? (1998년), 뤼프레히트 넨스티엘의 구판 (1998년)
• 앤서니 티센의 로터 카이트 페이지
• 모델 구축 계획 수립
• Magnus 효과를 이용한 풍력 발전 활용
• 처음으로 빛의 마그너스 효과를 관찰한 연구자들
• 퀀텀 매그리프트
• 비디오:마그너스 효과 적용