마스터 정리(알고리즘 분석)

알고리즘 분석에서 분할 및 재무 재발을 위한 마스터 정리는 많은 분할 및 정복 알고리즘 분석에서 발생하는 유형의 재발 관계에 대해 점증적 분석(Big O 표기법을 사용)을 제공한다.이 접근법은 존 벤틀리, 도로테아 하켄, 제임스 B에 의해 처음 제시되었다. 1980년 작센 주(州)^[1]에서는 이런 재발 문제를 해결하기 위한 '단일화 방식'으로 묘사되었다."마스터 정리"라는 이름은 널리 사용되는 알고리즘 교과서 코멘, Leiserson, Rivest, Stein이 쓴 알고리즘 소개에 의해 대중화되었다.

모든 재발 관계가 이 정리의 사용으로 해결될 수 있는 것은 아니다; 그것의 일반화에는 Akra-Bazi 방법이 포함된다.

소개

다음과 같은 재귀 알고리즘을 사용하여 해결할 수 있는 문제를 고려하십시오.

절차 p(크기 n의 입력 x): n < 어떤 상수 k: 다른 반복 없이 x를 직접 해결:각각 크기가 n/b인 x의 하위 문제 작성 각 하위 문제에 대해 반복적으로 호출 절차 p. 하위 문제의 결과 결합

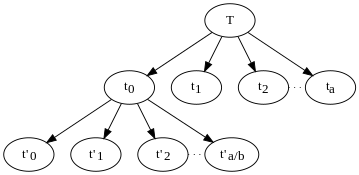
위의 알고리즘은 문제를 재귀적으로 여러 하위 문제로 나누는데, 각 하위 문제는 크기 n/b이다.솔루션 트리는 각 재귀 호출에 대한 노드를 가지고 있으며, 해당 노드의 하위 노드는 해당 호출에서 이루어진 다른 호출이다.나무의 잎은 재귀의 기본 케이스로, 재발하지 않는 하위 문제(k보다 작은 크기)이다.위의 예제는 각 잎이 아닌 노드에 하위 노드를 둘 수 있다.각 노드는 해당 재귀 호출 인스턴스에 전달되고 $f{\displaystyle }$(${\displaystyle n}$) ${\displaystyle f(n)}$이(가) 제공한 하위 문제의 크기에 해당하는 작업을 수행한다$.$전체 알고리즘에 의해 수행된 총 작업량은 트리의 모든 노드에 의해 수행된 작업의 합이다.

일반적으로 $T{\displaystyle }$( ${\displaystyle n}$) ${\displaystyle T(n$로 표시되는 크기 'n'의 입력에서 위의 'p'와 같은 알고리즘의 런타임은 반복 관계에 의해 표현될 수 있다.

$T(n)=a\;T\왼쪽({\frac {n}{b}\오른쪽)+f(n),}$

여기서 $f{\displaystyle }$(${\displaystyle n}$) ${\displaystyle f(n)}$은(는) 하위 문제를 생성하고 그 결과를 위의 절차에 결합하는 시간이다$$.이 방정식은 연속적으로 그 자체로 대체될 수 있고, 수행된 총 작업량에 대한 표현을 얻기 위해 확장될 수 있다.^[2]마스터 정리는 재귀적 관계의 확장을 하지 않고 이 형태의 많은 재귀적 관계를 직접 θ-notation으로 변환할 수 있도록 한다.

일반형식

마스터 정리는 입력을 동일한 크기의 작은 하위 문제로 분할하고 하위 문제를 재귀적으로 해결한 다음 하위 문제 해결 방법을 결합하여 원래의 문제에 대한 해결책을 제공하는 분할 및 정복 알고리즘으로부터의 재발을 항상 무증상적으로 엄격히 제한한다.그러한 알고리즘의 시간은 알고리즘의 재귀 호출에서 이루어진 시간과 함께 재귀의 최상위 수준에서 수행하는 작업(문제를 하위 문제로 나눈 다음 하위 문제 해결책들을 결합하는 작업)을 추가함으로써 표현할 수 있다.$T{\displaystyle }$(${\displaystyle n}$) ${\displaystyle$ $T(n$$)}$ 크기 $n{\displaystyle }$ ${\$$displaystyle$ $n}$및 $f{\displaystyle }$($)$ 입력에 대한 알고리즘의 총 시간을$$ 나타내는 경우$,$ 재발의 최상위 수준에서 소요된 시간을 나타내는$$ 다음 형식을 취하는 반복 관계에 의해 시간을 표시할 수 있다.

$T(n)=a\;T\!\왼쪽({\frac {n}{b}\오른쪽)+f(n)}$

여기서 $n{\displaystyle }$ ${\displaystyle n}$은(는) 입력 $문제$의$$크기, {\$displaystyle$ a}은$($는) 재귀의 하위 문제 수, $b{\displaystyle }$ ${\displaystyle b}$은(는) 각 재귀 호출(b)에서 하위 문제 크기가 감소되는 요인이다.아래의 정리도 재발을 위한 근거 사례로서 $T{\displaystyle }$( ${\displaystyle n}$)${\displaystyle }$= ${\displaystyle \mathrm{\theta }}$( 1${\displaystyle }$) ${\displaystyle T(n)=$라고 가정한다.$\Theta(1$) n {\displaystyle $n}$이(가$)$ 일부 바인딩 > ${\displaystyle \kappa >0}$보다 작을$$ 때$,$ 재귀 호출로 이어질 가장 작은 입력 크기

$문제$의 f (n $){\displaystyle$ f$(n)}$을(를) 분할/재결합하는 작업이$$ 임계 지수 c $c{\displaystyle {}_{}}$ c c c ${\displaystyle {\mathrm{crit}}_{}}$= ${\displaystyle {\log }_{}}$ ${\displaystyle b_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle a}$ ${\displaysty c_{\operatorname}}}=\log _{b}a$ (아래 표는 표준 빅 O 표기법을 사용한다.)

${\displaystyle c_{\probname {crit}}=\log _{b}a=\log(\#{\text{subproblems}})/\logdatableg\text{subproblem size}}}}$

케이스	설명	$c{\displaystyle {}_{}}$ c ${\displaystyle {\mathrm{crit}}_{}}$ ${\$에 대한$$ $f{\displaystyle }$ ${\displaystyle (n}$ ${\displaystyle )}$ ${\displaystyle f(n)}$의 조건$,$ 즉 ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle b_{}}$⁡ a ${\displaystyle \log_{b}a}$	마스터 정리 바인딩	공칭적 예
1	문제를 분리/재결합하기 위한 작업은 하위 문제에 의해 왜소하다. 즉, 재귀나무는 잎이 무성하다.	$f{\displaystyle }$( ${\displaystyle n}$)${\displaystyle }$= ${\displaystyle O}$( ${\displaystyle n^{}}$ c${\displaystyle {}^{}}$) ${\displaystyle f(n)=O(n^{c})}$ 여기서$$ < c ${\$ {$crit}}}}}}}}}}}}$ (낮은 지수 다항식에 의해 경계됨)	... 다음 $T{\displaystyle }$( ${\displaystyle n}$)${\displaystyle }$= ${\displaystyle \mathrm{\theta }}$(${\displaystyle {}^{}}$ ${\displaystyle {c{}_{}}^{}}$ c c ${\displaystyle {{\mathrm{crit}}_{}}^{}}$) ${\$$\theta \left(n^{c_{\operatorname {crit} }}}\오른쪽)}$ (분할 용어는 나타나지 않으며, 재귀 트리 구조가 지배적이다.)	$b{\displaystyle }$= ${\displaystyle {2\mathrm{}}^{}}$ ${\$ 및$$ $f{\displaystyle }$(${\displaystyle n}$)${\displaystyle }$= O${\displaystyle ({n\mathrm{}}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$/ 2${\displaystyle {}^{}}$- ${\displaystyle {ϵ}^{}}$) ${\displaystyle f(n)=O(n^{1/$${\displaystyle {2-\mathrm{}}^{}}$$\epsilon$ $\}\}\}\}\},$ $T{\displaystyle (n)}$= ${\displaystyle \mathrm{\theta }({}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$/ 2${\displaystyle {}^{}}$) ${\displaystystylean$ T$(n)=$$\Theta(n^{1/2$
2	문제를 분할/재결합하기 위한 작업은 하위 문제에 필적한다.	$f{\displaystyle }$(${\displaystyle n}$ )${\displaystyle }$= ${\displaystyle \mathrm{\theta }}$ ${\displaystyle ({}^{}}$ ${\displaystyle {c{}_{}}^{}}$ c c c c ${\displaystyle {{\mathrm{crit}}_{}}^{}}$ ${\displaystyle {\log }^{}{{}_{}}^{}{}^{}}$ ${\displaystyle k^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle n}$) ${\displaystyle f(n)=$인 경우$\theta(n^{c_{\operatorname {crit}}}}}}}}}}}{}\log ^{k}n)$을(를) $k{\displaystyle }$ ${\displaystyle \ge }$ ${\displaystyle 0}$ ${\displaystyle k\geq$ 0$}$에 대해 (임계값-임계값 다항식으로 범위 제한, 0회 이상 선택 ${\displaystyle \mathrm{로그}}$ ${\displaystyle \log }$)	... 다음 $T{\displaystyle }$( n${\displaystyle }$)${\displaystyle }$= ${\displaystyle \mathrm{\theta }}$ ${\displaystyle (n{}^{}}$ ${\displaystyle {c{}_{}}^{}}$ c c c c c ${\displaystyle {{\mathrm{crit}}_{}}^{}}$ ${\displaystyle {\log }^{}{{}_{}}^{}{}^{}}$ ${\displaystyle k^{}}$+ ${\displaystyle 1^{}}$⁡ ${\displaystyle n}$ )${\$$\theta \left(n^{c_{\operatorname {crit}}}}}}\log ^{k+1}n\right)}$ (바운드는 로그가 단일 전원에 의해 증강되는 분할 항이다.)	$b{\displaystyle }$= ${\displaystyle {2\mathrm{}}^{}}$ ${\$ 및 $f$(n ${\displaystyle )}$= ${\displaystyle \mathrm{\theta }({n\mathrm{}}^{}}$ 1${\displaystyle {}^{}}$/ ${\displaystyle {2\mathrm{}}^{}}$) ${\displaystyle f(n)=$$\theta (n^{1/2$})$$, 다음 T ${\displaystyle (n}$)${\displaystyle }$= ${\displaystyle \mathrm{\theta }}$(${\displaystyle {}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$/ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle \log \mathrm{logn}}$ ${\displaystyle )}$ ${\displaystyle$ T$(n)=$$\theta (n^{1/2}\log$ n$)}$. $b{\displaystyle }$= ${\displaystyle {2\mathrm{}}^{}}$ ${\$}}$$및$$ $f{\displaystyle }$(${\displaystyle n}$ ${\displaystyle )}$= ${\displaystyle \mathrm{\theta }}$ ${\displaystyle ({}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$/ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle \log }$ ${\displaystyle n}$) ${\displaystyle f(n)=$$\theta(n^{1/2}\log n$ 다음 $T{\displaystyle (n}$)${\displaystyle }$= ${\displaystyle \mathrm{\theta }({n\mathrm{}}^{}}$ 1${\displaystyle {}^{}}$/ 2 ${\displaystyle {\log }^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}n}$) ${\displaystyle T(n)=$$\theta (n^{1/2}\log ^{2}n$ .
3	문제를 분리/재결합하기 위한 작업이 하위 문제를 지배한다. 즉, 재귀나무는 뿌리째 뽑는다.	$f{\displaystyle }$( ${\displaystyle n}$)${\displaystyle }$= ${\displaystyle \mathrm{\Omega }}$(${\displaystyle n^{}}$ c${\displaystyle {}^{}}$) ${\displaystyle f(n)=\Oomega(n^{c}})$ 여기서$$ > c c ${\$ (대칭 다항식 하한)	...이것이 반드시 아무것도 산출하는 것은 아니다.게다가, 만약 ${\displaystyle a}$(${\displaystyle n\frac{}{}}$ ${\displaystyle \frac{b}{}}$) ${\displaystyle \le k}$ ${\displaystyle f}$ ${\displaystyle (n}$ ${\displaystyle )}$ ${\displaystyle af\left\frac\$frac {n}{$b$$}\$$오른쪽$)\$leq$ kf$(n$)} k<1 {\$displaystyle k<1$} $및{\displaystyle }$ 충분히$$큰 n {\$displaystyle n}($정규격 조건이라고 함)에 대한$$ 경우) 그러면 총계는 분할 용어 $f{\displaystyle (n}$) ${\displaystyle f(n)}$에 의해 지배된다$.$ $T\왼쪽(n\오른쪽)=\theta \left(f(n)\right)}$	$b{\displaystyle }$= ${\displaystyle {2\mathrm{}}^{}}$ ${\$}}$$및 f$$ ${\displaystyle (n}$)${\displaystyle }$= ${\displaystyle \mathrm{\Omega }}$ ${\displaystyle ({}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$/ ${\displaystyle {2\mathrm{}}^{}}$+ ${\displaystyle {ϵ}^{}}$) ${\displaystyle f(n)=\Oomega(n^{1/2+\epsilon }}}}}}}$이(가) 규칙성 조건이 유지되면 $T{\displaystyle (n}$)${\displaystyle }$= $(f$ ) $=$ $θ)({\d$)$\Theta$(f($n$

사례 2의 유용한 확장은 $k{\displaystyle }$ ${\displaystyle k}$의 모든 값을 처리한다$.$^[3]

케이스	$c{\displaystyle {}_{}}$ c ${\displaystyle {\mathrm{crit}}_{}}$ ${\$에 대한$$ $f{\displaystyle }$ ${\displaystyle (n}$ ${\displaystyle )}$ ${\displaystyle f(n)}$의 조건$,$ 즉 ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle b_{}}$⁡ a ${\displaystyle \log_{b}a}$	마스터 정리 바인딩	공칭적 예
2a	$f{\displaystyle }$(${\displaystyle n}$ )${\displaystyle }$= ${\displaystyle \mathrm{\theta }}$ ${\displaystyle ({}^{}}$ ${\displaystyle {c{}_{}}^{}}$ c c c c ${\displaystyle {{\mathrm{crit}}_{}}^{}}$ ${\displaystyle {\log }^{}{{}_{}}^{}{}^{}}$ ${\displaystyle k^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle n}$) ${\displaystyle f(n)=$인 경우$\theta$$n^{c_{\operatorname {crit}}$$}}}\$ $^{k}n)$ - 1 {\$displaystyle$ k$>-1}$	... 다음 $T{\displaystyle }$( n${\displaystyle }$)${\displaystyle }$= ${\displaystyle \mathrm{\theta }}$ ${\displaystyle (n{}^{}}$ ${\displaystyle {c{}_{}}^{}}$ c c c c c ${\displaystyle {{\mathrm{crit}}_{}}^{}}$ ${\displaystyle {\log }^{}{{}_{}}^{}{}^{}}$ ${\displaystyle k^{}}$+ ${\displaystyle 1^{}}$⁡ ${\displaystyle n}$ )${\$$\theta \left(n^{c_{\operatorname {crit}}}}}}\log ^{k+1}n\right)}$ (바운드는 로그가 단일 전원에 의해 증강되는 분할 항이다.)	$b{\displaystyle }$= ${\displaystyle {2\mathrm{}}^{}}$ ${\$}}$$및$$ $f{\displaystyle (n}$)${\displaystyle }$= ${\displaystyle \mathrm{\theta }({n\mathrm{}}^{}}$ 1${\displaystyle {}^{}}$/ 2${\displaystyle {}^{}}$/ ${\displaystyle {log\mathrm{}}^{}}$ 1${\displaystyle {}^{}}$/ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}n}$) ${\displaystyle f(n)=$$\theta(n^{1/2}/\log ^{1/2}n$ $T{\displaystyle (n}$ ${\displaystyle )}$= ${\displaystyle =({}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$/ 2 ${\displaystyle {log\mathrm{}}^{}}$ 1${\displaystyle {}^{}}$/ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}n}$) ${\displaystyle T(n)=$$\theta (n^{1/2}\log ^{1/2}n)}$.
2b	$f{\displaystyle }$(${\displaystyle n}$ )${\displaystyle }$= ${\displaystyle \mathrm{\theta }}$ ${\displaystyle ({}^{}}$ ${\displaystyle {c{}_{}}^{}}$ c c c c ${\displaystyle {{\mathrm{crit}}_{}}^{}}$ ${\displaystyle {\log }^{}{{}_{}}^{}{}^{}}$ ${\displaystyle k^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle n}$) ${\displaystyle f(n)=$인 경우$\theta(n^{c_{\operatorname {crit}$ }} $}}\log ^{k}n)$에서 ${\displaystyle \mathrm{k}}$=${\displaystyle }$- 1 ${\displaystyle$ k$=-1}$	... 다음 $T{\displaystyle }$( n${\displaystyle }$)${\displaystyle }$= ${\displaystyle \mathrm{\theta }}$(${\displaystyle {n{}_{}}^{}}$ ${\displaystyle c}$ c c c c c ${\displaystyle {{\mathrm{crit}}_{}}^{}}$ ${\displaystyle \log }$ ${\displaystyle }$ ${\displaystyle n}$) ${\$ T$(n)=$$\theta \left(n^{c_{\operatorname {crit}}}}}\log \log n\right)}$ (바운드는 로그 역수가 반복된 로그로 대체되는 분할 기간이다.)	$b{\displaystyle }$= ${\displaystyle {2\mathrm{}}^{}}$ ${\$}}$$및$$ $f{\displaystyle }$(${\displaystyle n}$)${\displaystyle }$= ${\displaystyle \mathrm{\theta }}$ ${\displaystyle ({}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$/ ${\displaystyle {2\mathrm{}}^{}}$/ ${\displaystyle \log }$ ${\displaystyle n}$) ${\displaystyle f(n)=$$\theta(n^{1/2}/\log n$ 다음 $T{\displaystyle (n}$)${\displaystyle }$=${\displaystyle }$=(${\displaystyle {}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$/ 2 ${\displaystyle \mathrm{로그}}$⁡ 로그${\displaystyle \mathrm{logn}}$) ${\displaystyle T(n)=$$\theta (n^{1/2}\log \log$ n$)}$.
2c	$f{\displaystyle }$(${\displaystyle n}$ )${\displaystyle }$= ${\displaystyle \mathrm{\theta }}$ ${\displaystyle ({}^{}}$ ${\displaystyle {c{}_{}}^{}}$ c c c c ${\displaystyle {{\mathrm{crit}}_{}}^{}}$ ${\displaystyle {\log }^{}{{}_{}}^{}{}^{}}$ ${\displaystyle k^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle n}$) ${\displaystyle f(n)=$인 경우$\theta(n^{c_{\operatorname {crit} }}}}}\log$^{$k}n)$을(를$$) 임의의< - {\$displaystyle$ k$<-1}$	... 다음 $T{\displaystyle }$( ${\displaystyle n}$)${\displaystyle }$= ${\displaystyle \mathrm{\theta }}$(${\displaystyle {}^{}}$ ${\displaystyle {c{}_{}}^{}}$ c c ${\displaystyle {{\mathrm{crit}}_{}}^{}}$) ${\$$\theta \left(n^{c_{\operatorname {crit} }}}\오른쪽)}$ (바운드는 로그가 사라지는 분할 항입니다.)	$b{\displaystyle }$= ${\displaystyle {2\mathrm{}}^{}}$ ${\$}}$$$및{\displaystyle }$ f$$${\displaystyle (n}$)${\displaystyle }$= ${\displaystyle \mathrm{\theta }({n\mathrm{}}^{}}$ 1${\displaystyle {}^{}}$/ ${\displaystyle {2\mathrm{}}^{}}$/ ${\displaystyle {\log }^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}n}$) ${\displaystyle f(n)=$$\theta(n^{1/2}/\log ^{2}n$ T${\displaystyle (n}$)${\displaystyle }$= ${\displaystyle \mathrm{\theta }({n\mathrm{}}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$/ 2${\displaystyle {}^{}}$) ${\displaystyle T(n)=$$\Theta(n^{1/2$

예

사례 1 예

${\displaystyle T(n)=8T\왼쪽({\frac {n}{2}}\오른쪽)+1000n^{2}}$

위의 공식에서 알 수 있듯이:

${\displaystyle a}$= ${\displaystyle 8,}$ b${\displaystyle }$= ${\displaystyle 2,}$ ${\displaystyle f(n}$ ${\displaystyle )}$= ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$ 그래서

${\$$O{\displaystyle }$$\left(n$^{c$}\right$ ${\displaystyle \mathrm{여기}}$서 c$$=${\displaystyle }$2 {\$displaystyle c=2}$

다음으로, 사례 1 조건을 충족하는지 확인하십시오.

a= 8= > c ${\displaystyle \log \log _${b}$a=\$log $_{2}8=3}c}$.

라고 하는 것은 마스터 정리의 첫 번째 사례에서 따온 것이다.

$[\displayplaystyle T(n)=\theta \left(n^{\log_{b}a}\right)=\theta \left(n^{3}\오른쪽)}$

($이{\displaystyle }$ ${\displaystyle \mathrm{결과}}$는 T (${\displaystyle }$${\displaystyle 1}$${\displaystyle }$) = ${\displaystyle {}^{}}$ ${\displaystyle {}^{}{displaystyle\mathrm{}}^{}}$ T(n) = $1001$n $3$- 1000 n 2 {\displaystyle T$($n${\displaystyle )=}$$1001n^{3}-1000n^{2$ T ( 1${\displaystyle }$)${\displaystyle }$= ${\displaystyle 1}$ ${\displaystytle T(1)=1}$을 가정하면 확인된다.

사례 2 예

${\displaystyle T(n)=2T\왼쪽({\frac {n}{2}}\오른쪽)+10n}$

위의 공식에서 알 수 있듯이 변수들은 다음과 같은 값을 얻는다.

${\displaystyle a=2,\,b=2,\,c=1,\,f(n)=10n}$

${\$$\theta \left(n^{c}\log ^{k}n\right)$ $여기$서 c${\displaystyle }$= ${\displaystyle 1}$,${\displaystyle k}$= ${\displaystyle 0}$ ${\displaystyle c=1,k=0}$

다음으로, 사례 2 조건을 충족하는지 확인하십시오.

${\displaystyle {\log }_{}}$ ${\displaystyle b_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle a}$= ${\displaystyle {\log }_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle 2}$= 1 ${\displaystyle \log _{b}a=\log _{2}2=1$ 따라서 c와 $l{\displaystyle }$ ${\displaystyle o_{}}$ ${\displaystyle {}_{}}$ a ${\displaystyle log_{b}a}$는 동일하다$$.

그래서 마스터 정리의 두 번째 사례에서 다음과 같다.

$[\displayplaystyle T(n)=\theta \left(n^{\log _{b}a}\log ^{k+1}n\right)=\theta \left(n^{1}\log ^{1}n\right)=\theta \left(n\log n\right)}$

따라서 주어진 재발관계 T(n)는 θ(n log n)에 있었다.

($이{\displaystyle }$ ${\displaystyle \mathrm{결과}}$는 T${\displaystyle }$( n${\displaystyle }$)${\displaystyle }$= n${\displaystyle }$+ ${\displaystyle 10}$ ${\displaystyle n}$ ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle {2\mathrm{}}_{}\mathrm{2n}}$ ${\displaystyle T(n)=n+10n\log_{2}n$ T${\displaystyle }$( ${\displaystyle 1}$)${\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle T(1)=1}$을 가정하여 정확한 재발 관계 해법으로 확인된다.)$$

사례 3 예

${\displaystyle T(n)=2T\왼쪽({\frac {n}{2}}\오른쪽)+n^{2}}$

위의 공식에서 알 수 있듯이 변수들은 다음과 같은 값을 얻는다.

${\displaystyle a=2,\,b=2,\,f(n)=n^{2}}$

${\displaystyle f}$( n${\displaystyle }$)${\displaystyle }$= ${\displaystyle \mathrm{\Omega }}$ ${\displaystyle ({}^{}}$ ${\displaystyle c^{}}$) ${\$ ${\displaystyle \mathrm{여기}}$서 c${\displaystyle }$= 2 ${\displaystyle c=2$}

다음으로 사례 3 조건을 충족하는지 확인하십시오.

${\displaystyle {\log }_{}}$ ${\displaystyle b_{}{log\mathrm{}}_{}}$ a = log 2 ${\displaystyle {}_{}}$ ${\displaystyle 2}$= 1 ${\displaystyle \log$ \log $_{b}a=\log _{2}=1$ 따라서 yes, > b a ${\displaystyle$ c$>\log _{b}a}$

규칙성 조건도 다음을 유지한다.

$2$( ${\displaystyle n\frac{{}^{}}{}}$ ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{\mathrm{}}}$) ${\displaystyle \le {}^{}}$ ${\displaystyle {n\mathrm{}}^{}}$ 2 ${\$ {$n^{2}}:{4}\오른쪽)\leq kn^{$2$\}\},$ $k{\displaystyle }$ =${\displaystyle 1}$/ ${\displaystyle 2\mathrm{}}${\$displaysty k=1/$2}} $선택$

그래서 마스터 정리의 세 번째 경우에서 다음과 같다.

$T\왼쪽(n\오른쪽)=\theta \left(f(n)\right)=\theta \left(n^{2}\오른쪽).}$

따라서 주어진 반복 관계 $T{\displaystyle }$( ${\displaystyle n}$) ${\displaystyle T(n)}$은(는) $원래$ 공식의 f${\displaystyle }$( n${\displaystyle }$) ${\$$displaystyle \Theta($${\displaystyle n}$$^{2})$를 준수하는$$$\theta {\displaystyle \mathrm{}}$(${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$) ${\$$displaystystyle f(n)}$에 있었다$$.

($이{\displaystyle }$ 결과는 T (${\displaystyle n}$)${\displaystyle }$= 2 ${\displaystyle \mathrm{n}}$ -${\displaystyle {}^{}2}$ - n$${\$displaystyle T(n)=2n^{2}-n$${\displaystyle }$T (${\displaystyle 1}$) = ${\displaystyle 1}${\$displaystyle T$(1$)=1}$을 가정하여 정확한 재발 관계 해법으로 확인된다.)$$

허용되지 않는 방정식

마스터 정리를 사용하여 다음과 같은 방정식을 풀 수 없다.^[4]

• ${\displaystyle T(n)=2^{n}T\왼쪽({\frac {n}{2}}\오른쪽)+n^{n}}}$

  a는 상수가 아니다. 하위 문제 수는 고정되어야 한다.

• ${\displaystyle T(n)=2T\왼쪽({\frac {n}{2}}\오른쪽)+{\frac {n}{\logn}}}}$

  $f{\displaystyle }$(${\displaystyle n}$) ${\displaystyle f(n)}$과(와) $n{\displaystyle {}^{}}$ ${\displaystyle {{log}_{}}^{}}$ b의 비항명적 $({\$ n$^{\log _{b}a})($아래 참조, 확장 버전이 적용됨)

• $T(n)=0.5T\왼쪽({\frac {n}{2}}\오른쪽)+n}$

  $[\displaystyle a<1})$은 하나의 하위 문제를 가질 수 없다.

• $T(n)=64T\왼쪽({\frac {n}{8}\오른쪽)-n^{2}\log n}$

  ${\displaystyle f}$( ${\displaystyle n}$) ${\displaystyle f(n$ 즉 조합 시간이 양수가 아님

• $[\displayplaystyle T(n)=T\왼쪽({\frac {n}{2}}\오른쪽)+n(2-\cos n)}$

  사건 3은 규칙 위반이다.

In the second inadmissible example above, the difference between ${\displaystyle f(n)}$ and ${\displaystyle n^{\log _{b}a}}$ can be expressed with the ratio ${\displaystyle {\frac {f(n)}{n^{\$$log _{b}a}}}={\frac {n/\log n}{n^{\log _{2}2}}}={\frac {n}{n\log n}}={\frac {1}{\log n}}}$. It is clear that ${\displaystyle {\frac {1}{\log n}}<n^{\epsilon }}$ for any constant ${\displaystyle \epsilon >0}$.따라서 그 차이는 다항식이 아니며 마스터 정리의 기본 형태는 적용되지 않는다.확장형(사례 2b)이 적용되며, $솔루션{\displaystyle }$ T${\displaystyle }$( ${\displaystyle n}$)${\displaystyle }$= ${\displaystyle \mathrm{\theta }}$ ${\displaystyle (n}$ ${\displaystyle \log }$ log ${\displaystyle \log }$ ${\displaystyle }$ n${\displaystyle }$) ${\displaystyle T(n)=$가 제공된다.$\Theta(n\log \log$ n$)\}.$

공통 알고리즘에 적용

알고리즘.	재발관계	런타임	댓글
이진 검색	$[\displayplaystyle T(n)=T\왼쪽({\frac {n}{2}}\오른쪽)+O(1)}$	${\displaystyle O(\log n)}$	마스터 정리 사례 $적용{\displaystyle }$ c${\displaystyle }$= ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle b_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle a}$ ${\displaystyle$ c$=\log _{b}a$ $여기$서 a${\displaystyle }$= ${\displaystyle 1,b}$ =${\displaystyle 2}$,${\displaystyle c}$ = ${\displaystyle 0,k}$ = $,$ 0 {\$displaystyle a=1,b=2,c=0,k=0}$
이진 트리 통과	${\displaystyle T(n)=2T\왼쪽({\frac {n}{2}}\오른쪽)+O(1)}$	${\displaystyle O(n)}$	마스터 정리 c< a ${\displaystyle$ c$<\log$ ${\displaystyle \mathrm{\_}}$${b}a}$ 여기서 $a{\displaystyle }$ = 2,${\displaystyle \mathrm{b}}$=${\displaystyle }$2, ${\displaystyle c}$=${\displaystyle 0}$ ${\displaystyle a=2,b=2,c=0}$
최적 정렬 행렬 검색	${\displaystyle T(n)=2T\left({\frac {n}{2}}\오른쪽)+O(\log n)}$	${\displaystyle O(n)}$	$p{\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle p=1}$ 및$$ $g{\displaystyle }$ (${\displaystyle u}$) = ${\displaystyle \log }$ ${\displaystyle }$ (${\displaystyle u}$) ${\displaystyle g(u)=\log(u)}$에 Akra-Bazi 정리를 적용하여$$ $\theta {\displaystyle \mathrm{}}$(${\displaystyle \mathrm{2n}}$ -${\displaystyle \log }$ ${\displaystyle }$ ${\displaystyle n}$) ${\displaystystyle \Teta(2n-\log n)})}$
병합 정렬	${\displaystyle T(n)=2T\왼쪽({\frac {n}{2}}\오른쪽)+O(n)}$	${\displaystyle O(n\log n)}$	마스터 정리 케이스 $적용{\displaystyle }$ c${\displaystyle }$= ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle b}$ ${\displaystyle {}_{}}$ a ${\displaystyle$ c$=\log _{b}a$ 여기서 $a{\displaystyle }$= ${\displaystyle 2,}$ b${\displaystyle }$= 2${\displaystyle ,}$ ${\displaystyle c}$= ${\displaystyle 1,}$ ${\displaystyle k}$= ${\displaystyle 1}$ ${\displaystyle a=2,b=2,c=1,k=1$}

참고 항목

• 아크라-바찌법
• 점근 복잡성

메모들

참조

• 토마스 H. 코멘, 찰스 E. Leiserson, Ronald L. Rivest, Clifford Stein.알고리즘 소개, Second Edition.MIT 프레스와 맥그로-힐, 2001.ISBN 0-262-03293-7섹션 4.3 (마스터 방식)과 4.4 (마스터 정리 증명), 페이지 73–90.
• 마이클 T. 굿리치와 로베르토 타마시아.알고리즘 설계: 기초, 분석 및 인터넷 예제.와일리, 2002년ISBN 0-471-38365-1.마스터 정리(CLRS의 정리보다 강한 여기에 포함된 사례 2의 버전을 포함)는 페이지 268–270에 수록되어 있다.

외부 링크

• 테오레마 메스트레 e Prescios Resolvidos (포르투갈어)