바이너리 검색

바이너리 검색

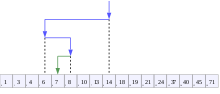7이 목표값인 바이너리 검색 알고리즘의 시각화
클래스	검색 알고리즘
데이터 구조	배열
최악의 경우 공연	O(log n)
베스트 케이스 공연	O(1)
평균 공연	O(log n)
최악의 경우 공간 복잡성	O(1)

컴퓨터 과학에서 반간격 검색,^[1] 로그 검색 ^[2]또는 바이너리 잘라내기라고도 하는 바이너리 검색은 정렬된 배열 내에서 목표값의 위치를 찾는 검색 알고리즘이다.^[3][4][5]이진 검색은 대상 값을 배열의 중간 요소와 비교한다.동일하지 않으면 대상이 거짓말을 할 수 없는 절반은 제거되고 나머지 절반은 검색이 계속되며, 다시 중간 요소를 취하여 목표값과 비교한 후 목표값이 발견될 때까지 이를 반복한다.나머지 절반은 비어 있는 상태로 검색이 종료되면 대상이 배열에 없는 것이다.

이진 검색은 최악의 경우 로그 시간으로 실행되어 $O{\displaystyle (\log }$ ${\displaystyle n}$) ${\displaystyle$ O$(\log$ n$)}$을(를) 비교하며, 여기서 $n{\displaystyle }$ ${\displaystyle n}$은 배열의 요소 수입니다.^[a][6]바이너리 검색은 작은 배열을 제외하고 선형 검색보다 빠르다.그러나 이진 검색을 적용할 수 있으려면 배열을 먼저 정렬해야 한다.해시 테이블 등 빠른 검색을 위해 설계된 전문 데이터 구조가 있어 바이너리 검색보다 더 효율적으로 검색할 수 있다.그러나 이진 검색은 배열에 없더라도 대상을 기준으로 배열에서 다음으로 작거나 다음으로 큰 요소를 찾는 등 보다 광범위한 문제를 해결하는 데 사용될 수 있다.

바이너리 검색에는 수많은 변형이 있다.특히 분수 계단식 계단식 배열은 여러 어레이에서 동일한 값에 대한 이진 검색 속도를 높인다.분수 계단식 계단식 배열은 계산 기하학 및 기타 여러 분야에서 많은 검색 문제를 효율적으로 해결한다.지수 검색은 이진 검색을 바인딩되지 않은 목록으로 확장한다.바이너리 검색 트리와 B-트리 데이터 구조는 바이너리 검색을 기반으로 한다.

알고리즘.

이진 검색은 정렬된 배열에서 작동한다.바이너리 검색은 배열 중간에 있는 요소를 목표값과 비교하는 것으로 시작한다.목표값이 요소와 일치하면 배열에서 해당 위치가 반환된다.대상 값이 요소보다 작으면 배열의 하위 절반에서 검색이 계속된다.대상 값이 요소보다 크면 배열의 위쪽 절반에서 검색이 계속된다.이렇게 함으로써 알고리즘은 각 반복에 목표값이 존재할 수 없는 절반을 제거한다.^[7]

절차

Given an array ${\displaystyle A}$ of ${\displaystyle n}$ elements with values or records ${\displaystyle A_{0},A_{1},A_{2},\ldots ,A_{n-1}}$sorted such that ${\displaystyle A_{0}\leq A_{1}\leq A_{2}\leq \cdots \leq A_{n-1}}$, and대상 값 $T{\displaystyle }$ ${\displaystyle$ T$\},$ 다음 서브루틴은 이진 검색을 사용하여 $A{\displaystyle }$ ${\displaystyle A}$에서 $T{\displaystyle }$ ${\displaystyle T}$의 인덱스를 찾는다$.$^[7]

1. $L$ ${\$$displaystyle$ $L}$을(를) $0$으로$,$ $R$ ${\displaystyle R}$을$($를$)$ n${\displaystyle }$- ${\displaystyle 1}$로 설정하십시오$.$
2. > ${\displaystyle L>R$인 경우 검색이 실패한 것으로 종료된다.
3. $m{\displaystyle \frac{}{}}$ ${\displaystyle$ m}($중간$ 요소의 위치$)$을 $L{\displaystyle \frac{}{}}$ + ${\displaystyle \frac{R}{}}$ 2 ${\$L${\displaystyle \frac{}{}}$+ R ${\displaystyle \frac{\mathrm{}}{}}$ ${\$}보다 작거나 같은 최대 정수인 L${\displaystyle \frac{}{}}$+ R 2의 ${\displaystyle \frac{}{}}$에 설정하십시오$.$
4. < ${\displaystyle A_{m$$T}$인 경우 $L{\displaystyle }$ ${\displaystyle L}$을(를) m${\displaystyle }$+ ${\displaystyle 1}$ ${\displaystyle m+1}($)로$$ 설정하고$$ 2단계로 이동하십시오.
5. m> ${\displaystyle A_{m}$인 경우$T$ $R{\displaystyle }$ ${\displaystyle R}$을(를) $m{\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle m-1}($으)로$$ 설정하고$$ 2단계로 이동하십시오.
6. 이제 $A{\displaystyle {}_{}}$ ${\displaystyle m_{}}$= ${\displaystyle T}$ ${\displaystyle A_{m}=T$ 검색이 완료됨; $반환{\displaystyle }$ m ${\displaystyle m$

이 반복적 절차는 두 $변수{\displaystyle }$ L ${\displaystyle L$$}$ $및{\displaystyle }$ R$${\$displaystyle R}$을(를) 사용하여 검색 경계를 추적한다$.$ 절차는 다음과 같이 가성으로 나타낼 수 있으며, 여기서 변수 이름과 유형은 위와 동일하다.floor바닥 기능이며,unsuccessful검색의 실패를 전달하는 특정 가치를 말한다.^[7]

함수 binary_search(A, n, T)는 L := 0 R := n - 1인 반면 L ≤ R do m := 바닥(L + R) / 2) A[m] < T인 경우 L :=m + 1인 경우 R := m - 1: return m return 실패

또는 알고리즘이 $L{\displaystyle \frac{}{}}$+ ${\displaystyle \frac{R}{}}$ ${\displaystyle \frac{\mathrm{}}{}}$ ${\$의 천장을 취할 수 있다$.$ 이는 대상 값이 배열에서 두 번 이상 나타나면 결과가 달라질 수 있다.

대체절차

위의 절차에서 알고리즘은 모든 반복에서 ${\displaystyle }$ 요소$(m$ {\$displaystyle$ m}$$$)$가 대상(${\displaystyle }$ ${\displaystyle$ T$\})$과 동일한지 여부를 점검한다.일부 구현에서는 반복할 때마다 이 검사를 생략한다.$알고리즘$은 한 요소가 남아 있을 때만 이$$를 $수행$한다(L = R {\displaystyle $L=R}).$이것은 평균적으로 한 번의 반복이 더 필요한 반면, 한 번의 비교는 반복당 제거되기 때문에 더 빠른 비교 루프를 초래한다.^[8]

헤르만 보텐브루흐는 1962년에 이 수표를 생략한 최초의 시행을 발표했다.^[8][9]

1. $L$ ${\$$displaystyle$ $L}$을(를) $0$으로$,$ $R$ ${\displaystyle R}$을$($를$)$ n${\displaystyle }$- ${\displaystyle 1}$로 설정하십시오$.$
2. $L{\displaystyle }$ ${\displaystyle \ne }$ ${\displaystyle R}$ ${\displaystyle L\neq R}$ 동안$,$
   1. $m{\displaystyle \frac{}{}}$ ${\$${\displaystyle \frac{\mathrm{}}{}}$ m}($중간$ 요소의 위치$)$을 $L{\displaystyle \frac{}{}}$ + R 2 ${\$ L${\displaystyle \frac{}{}}$+ R ${\displaystyle \frac{2}{}}$ ${\$보다 크거나 같은 최소 정수인 L${\displaystyle \frac{}{}}$+ ${\displaystyle \frac{R}{}}$ ${\displaystyle \frac{}{}}$의 천장으로 설정하십시오$.$
   2. m> ${\displaystyle A_{m}$인 경우$T$ $R{\displaystyle }$ ${\displaystyle R}$을(를) m${\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle m-1}($으)로$$ 설정하십시오$.$
   3. $그렇지{\displaystyle }$ 않으면 $A{\displaystyle {}_{}}$ ${\displaystyle m_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle T}$ ${\displaystyle A_{m}\leq T$ L ${\displaystyle L}$을(를) $m{\displaystyle }$ ${\displaystyle m}($으)로$$ 설정하십시오$.$
3. 이제 $L{\displaystyle }$= ${\displaystyle R}$ ${\displaystyle L=R$ 검색이 완료됨.${\displaystyle L_{}}$= ${\displaystyle T}$ ${\displaystyle A_{L}=T$인 경우 $L{\displaystyle }$ ${\displaystyle L}$을(를) 반환하고$,$ 그렇지 않으면 검색이 실패한 것으로 종료된다.

어디에ceil천장 함수로서, 이 버전의 유사 부호는 다음과 같다.

함수 binary_search_alternative(A, n, T)는 L := 0 R :=n - 1인 반면 L != R do m := ceil(((L + R) / 2) A[M] > T이면 R := m : 1: A[L] = T이면 L : = 반환 L이 실패함수

중복 요소

이 절차에서는 배열에 중복 요소가 있더라도 요소가 목표값과 동일한 인덱스를 반환할 수 있다.예를 들어 검색할 배열이${\displaystyle }$[${\displaystyle 1,}$ 2,${\displaystyle 3}$,${\displaystyle 4}$,${\displaystyle }$4,${\displaystyle 4}$, ${\displaystyle 5}$,${\displaystyle }$6,${\displaystyle 7}$이고 대상이 [$1,2,$3,$4,4,5,6,7$]인 경우, 알고리즘이 4 ${\displaystyle 4}$인 경우$,$ 4번째(인덱스 3) 또는 5번째(인덱스 4) 요소를 반환하는 것이 정확할 것이다.정규 절차는 이 경우 네 번째 요소(지수 3)를 반환한다.항상 첫 번째 중복 항목을 반환하지는 않는다(${\displaystyle \mathrm{고려}}{\displaystyle }$[ 1,${\displaystyle 2}$,${\displaystyle 4}$,${\displaystyle 4}$,${\displaystyle }$4,${\displaystyle 5}$, ${\displaystyle 6}$,${\displaystyle 7}$ ${\displaystyle ]}$ ${\displaystyle$ [$1,2,4,4$,4,$4,5,6,7],$4$$,4,4,6,7],4,4,6,7을 반환하고,4는 여전히 4번째 요소를 반환한다.그러나 배열에서 중복되는 목표값에 대해서는 가장 왼쪽 또는 가장 오른쪽 요소를 찾아야 하는 경우가 있다.위의 예에서 4번째 요소는 값 4의 가장 왼쪽 요소인 반면, 5번째 요소는 값 4의 가장 오른쪽 요소인 것이다.위의 대체 절차는 그러한 요소가 존재하는 경우 항상 가장 오른쪽 요소의 지수를 반환한다.^[9]

가장 왼쪽 요소를 찾는 절차

가장 왼쪽 요소를 찾으려면 다음 절차를 사용할 수 있다.^[10]

1. $L{\displaystyle }$ ${\displaystyle$ $L$$}$을(를) $0$으로$,$ R$$ ${\$$displaystyle R$$}$을(를$)$ $n$으로 설정하십시오$.$
2. < R ${\displaystyle L>R}$ 동안
   1. $m{\displaystyle \frac{}{}}$ ${\displaystyle$ m}($중간$ 요소의 위치$)$을 $L{\displaystyle \frac{}{}}$ + ${\displaystyle \frac{R}{}}$ 2 ${\$L${\displaystyle \frac{}{}}$+ R ${\displaystyle \frac{\mathrm{}}{}}$ ${\$}보다 작거나 같은 최대 정수인 L${\displaystyle \frac{}{}}$+ R 2의 ${\displaystyle \frac{}{}}$에 설정하십시오$.$
   2. < ${\displaystyle A_{m$$T}$인 $경우{\displaystyle }$ L ${\displaystyle L}$을(를) ${\displaystyle \mathrm{m}}$+ 1 ${\displaystyle m+1}$로 설정하십시오$.$
   3. $그렇지{\displaystyle }$ 않으면 $A{\displaystyle {}_{}}$ m${\displaystyle {}_{}{m}_{}}$ ${\displaystyle T}$ ${\displaystyle A_{m}\geq T$ R ${\displaystyle R}$을(를) $m{\displaystyle }$ ${\displaystyle m}($으)로$$ 설정하십시오$.$
3. $L{\displaystyle }$ ${\displaystyle L}$을(를) 반환하십시오$.$

T{T\displaystyle}의 배열에 있는 T{T\displaystyle}일 만약 나는<>n{\displaystyle L<, n}과 L)T{\displaystyle A_{나는}=T}, thenAL{\displaystyle A_{나는}}은 제일 왼쪽의 요소. 비록 T{T\displaystyle}배열에 있지 않다, L{L\displaystyle}은 계급, 또는 n.짙은 갈색$배열$에서$$T {\$displaystyle$T$\}$보다 작은 요소의 .

어디에floor바닥 기능이며, 이 버전의 유사 부호는 다음과 같다.

함수 binary_search_left(A, n, T): L := 0 R := n인 반면 L < R : m : : = 바닥(L + R) / 2) A[m] < T : L : = m + 1 다른 : R : m return L

가장 오른쪽 요소를 찾는 절차

가장 오른쪽 요소를 찾으려면 다음 절차를 사용할 수 있다.^[10]

1. $L{\displaystyle }$ ${\displaystyle$ $L$$}$을(를) $0$으로$,$ R$$ ${\$$displaystyle R$$}$을(를$)$ $n$으로 설정하십시오$.$
2. < R ${\displaystyle L>R}$ 동안
   1. $m{\displaystyle \frac{}{}}$ ${\displaystyle$ m}($중간$ 요소의 위치$)$을 $L{\displaystyle \frac{}{}}$ + ${\displaystyle \frac{R}{}}$ 2 ${\$L${\displaystyle \frac{}{}}$+ R ${\displaystyle \frac{\mathrm{}}{}}$ ${\$}보다 작거나 같은 최대 정수인 L${\displaystyle \frac{}{}}$+ R 2의 ${\displaystyle \frac{}{}}$에 설정하십시오$.$
   2. m> ${\displaystyle A_{m}$인 경우$T$ $R{\displaystyle }$ ${\displaystyle R}$을(를) $m{\displaystyle }$ ${\displaystyle$ m$}(으$)로$$ 설정하십시오$.$
   3. 그렇지 않으면 $A{\displaystyle {}_{}}$ m${\displaystyle {}_{}{m}_{}}$ ${\displaystyle T}$ ${\displaystyle A_{m}\leq T$ $L{\displaystyle }$ ${\displaystyle L}$을(를) ${\displaystyle \mathrm{m}}$+ 1$(\displaystyle m+1}($으)로$$ 설정하십시오$.$
3. $R{\displaystyle }$ -${\displaystyle 1}$ ${\displaystyle R-1}$을(를) 반환하십시오$.$

는 T{T\displaystyle}일 만약 R>0{\displaystyle R>0}과 R− 1)T{\displaystyle A_{R-1}=T}, thenAR− 1{\displaystyle A_{R-1}}은는 최우측 요소. 비록 T{T\displaystyle}이 배열에 있지 않다 n−는 배열이 촉에 있는 요소의 R{\displaystyle n-R}이다.egrea$T{\displaystyle }$ ${\displaystyle T}$보다 작다$.$

어디에floor바닥 기능이며, 이 버전의 유사 부호는 다음과 같다.

함수 binary_search_rightmost(A, n, T): L := 0 R := n, L < A :m] > T : R : 1이면 바닥(L + R) / 2) R : R : : := m + 1 리턴 R - 1

근사 일치

위의 절차는 정확한 일치만 수행하여 목표값의 위치를 찾는다.그러나 바이너리 검색은 정렬된 배열에서 작동하기 때문에 대략적인 일치를 수행하기 위해 바이너리 검색을 확장하는 것은 사소한 일이다.예를 들어, 바이너리 검색은 주어진 값의 순위(작은 요소의 수), 선행 요소(다음 가장 작은 요소), 후속 요소(다음 가장 큰 요소) 및 가장 가까운 인접 요소를 계산하는 데 사용될 수 있다.두 값 사이의 요소 수를 찾는 범위 쿼리는 두 개의 순위 쿼리로 수행할 수 있다.^[11]

• 순위 쿼리는 가장 왼쪽 요소를 찾는 절차로 수행할 수 있다.목표값보다 작은 요소의 수는 절차에 의해 반환된다.^[11]
• 이전 쿼리는 순위 쿼리로 수행할 수 있다.목표값의 순위가 $r{\displaystyle }$ ${\displaystyle r}$인 경우$,$ 이전 $값$은 ${\displaystyle \mathrm{r}}$- 1 ${\displaystyle r-1}$이다$.$^[12]
• 후속 조회의 경우 가장 오른쪽 요소를 찾는 절차를 사용할 수 있다.대상 값에 대한 절차를 실행한 결과가 $r{\displaystyle }$ ${\displaystyle r}$인 경우$,$ 대상 값의 후속 값은 ${\displaystyle \mathrm{r}}$+ 1$${\$displaystyle$ r$+1}$이다$.$^[12]
• 목표값의 가장 가까운 이웃은 전임자 또는 후임자 중 더 가까운 쪽이다.
• 범위 쿼리도 간단하다.^[12]일단 두 값의 순위가 알려지면 첫 번째 값보다 크거나 같고 두 번째 값보다 작은 원소의 수는 두 값의 차이다.이 카운트는 범위의 끝점을 범위의 일부로 간주해야 하는지 여부 및 어레이에 해당 끝점과 일치하는 항목이 포함되어 있는지 여부에 따라 하나씩 위 또는 아래로 조정할 수 있다.^[13]

퍼포먼스

비교 횟수로 볼 때 이진수 검색의 성능은 이진수 트리에서 프로시저 실행을 보고 분석할 수 있다.트리의 루트 노드는 배열의 중간 요소다.하반부의 중간 요소는 뿌리의 왼쪽 자식 노드, 상반부의 중간 요소는 뿌리의 오른쪽 자식 노드다.그 나무의 나머지 부분은 비슷한 방식으로 지어져 있다.루트 노드에서 시작하여, 대상 값이 고려 중인 노드보다 작거나 많은지 여부에 따라 왼쪽 또는 오른쪽 하위 트리가 통과된다.^[6][14]

In the worst case, binary search makes ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$ iterations of the comparison loop, where the ${\textstyle \lfloor \rfloor }$ notation denotes the floor function that yields the greatest integer less than or equal to the argument, and ${\textstyle \log _{2}$${}$이(가) 이진 로그.이는 검색이 트리의 가장 깊은 레벨에 도달했을 때 최악의 경우에 도달하며, 어떤 이진 검색도 트리에 항상 $\lfloor$ ${\mathrm{로그}}_{}$ ${2\mathrm{}}_{}$ ${}_{}$($n$)$$+ $1$ $\rfloor$ ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$ 레벨이$$ 있기 때문이다.

최악의 경우는 대상 요소가 배열에 없을 때도 도달할 수 있다.$n$ ${\textstyle n}$이(가) 2의 검정력보다 1보다 작으면 항상 이 경우에 해당된다.그렇지 않으면, 검색이 트리의 가장 깊은 레벨에 도달한 경우$$the ${\mathrm{로그}}_{}$ ${2\mathrm{}}_{}$ ${}_{}$($n$)$$+ $1$ $\rfloor$ (\$textstyle \lllloor \log _{2}(n)+1\rfloor }$번$$ 반복하여 검색이 수행될 수 있다.그러나 $\lfloor$ ${\mathrm{로그}}_{}$ ${2\mathrm{}}_{}$ ${}_{}$($n$ $)$ $\rfloor$ ${\textstyle \llloor \log$ \llloor \log $_{2}(n)\rfloor }$회 반복할$$ 수 있는데, 이는 검색이 트리의 두 번째 가장 깊은 수준에서 종료될 경우 최악의 경우보다 한 번 적은 것이다.^[15]

On average, assuming that each element is equally likely to be searched, binary search makes ${\displaystyle \lfloor \log _{2}(n)\rfloor +1-(2^{\lfloor \log _{2}(n)\rfloor +1}-\lfloor \log _{2}(n)\rfloor -2)/n}$ iterations when the target element진열되어 있다.이는 대략 ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$(${\displaystyle n}$)${\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle \log _{2}(n)-1}$번$$ 반복과 같다.When the target element is not in the array, binary search makes ${\displaystyle \lfloor \log _{2}(n)\rfloor +2-2^{\lfloor \log _{2}(n)\rfloor +1}/(n+1)}$ iterations on average, assuming that the range between and outside elements is equally likely to be searched.^[14]

최적의 경우, 목표값이 배열의 중간 요소인 경우, 그 위치는 한 번 반복한 후에 반환된다.^[16]

반복의 측면에서 요소 비교만으로 작동하는 검색 알고리즘은 바이너리 검색보다 평균과 최악의 성능을 나타낼 수 없다.이진수색을 나타내는 비교 트리는 가장 낮은 수위 이상의 모든 레벨이 완전히 채워지기 때문에 가능한 가장 적은 레벨을 가진다.^[b]그렇지 않으면, 검색 알고리즘은 반복에서 몇 개의 요소를 제거하여 평균과 최악의 경우에 필요한 반복 횟수를 증가시킬 수 있다.이것은 비교에 기초한 다른 검색 알고리즘의 경우에 해당하며, 그것들이 일부 목표값에서 더 빠르게 작용하지만, 모든 요소에 대한 평균 성능은 이진 검색보다 더 나쁘다.배열을 반으로 나누면 바이너리 검색은 두 하위선의 크기가 최대한 유사함을 보장한다.^[14]

공간 복잡성

바이너리 검색에는 요소에 대한 세 개의 포인터가 필요하며, 이는 배열의 크기와 상관없이 배열 인덱스 또는 메모리 위치에 대한 포인터가 될 수 있다.따라서 이진 검색의 공간 복잡성은 연산 RAM 모델에서$$ O${\displaystyle }$( $1{\displaystyle }$) ${\displaystyle$ O$(1)}$이다.

평균 케이스의 파생

이항 검색에 의해 수행되는 평균 반복 횟수는 검색되는 각 요소의 확률에 따라 달라진다.성공적 검색과 실패적 검색의 경우는 평균적으로 다르다.성공적인 검색을 위해 각 요소가 동등하게 검색될 가능성이 있다고 가정할 것이다.실패한 검색의 경우 요소 간 및 외부 요소 간격이 동일하게 검색될 가능성이 있다고 가정할 것이다.검색에 성공한 평균 사례는 모든 요소를 정확히 한 번 검색하는 데 필요한 반복 횟수를 $n{\displaystyle }$ ${\displaystyle n$ 요소 수로 나눈 값이다.검색에 실패한 평균 사례는 정확하게 한 번 간격마다 요소를 검색하는 데 필요한 반복 횟수를 $n{\displaystyle }$+ ${\displaystyle 1}$ ${\displaystyle n+1}$ 간격으로$$ 나눈 값이다.^[14]

검색 성공

이진 트리 표현에서 성공적인 검색은 내부 경로라고 불리는 루트에서 대상 노드까지의 경로로 나타낼 수 있다.경로의 길이는 경로가 통과하는 에지 수(노드 간 연결)이다.해당 경로에 길이 $l{\displaystyle }$ ${\displaystyle l}$이$($가) 있는 경우 검색으로 수행되는 반복 횟수는 초기 반복을 계산하는$$ $l{\displaystyle }$+ ${\displaystyle 1}$ ${\displaystyle$ l$+1}$이다.내부 경로 길이는 모든 고유 내부 경로의 길이를 합한 값이다.루트부터 단일 노드까지의 경로는 하나뿐이므로, 각각의 내부 경로는 특정 요소에 대한 검색을 나타낸다.If there are ${\displaystyle n}$ elements, which is a positive integer, and the internal path length is ${\displaystyle I(n)}$, then the average number of iterations for a successful search ${\displaystyle T(n)=1+{\frac {I(n)}{n}}}$, with the one iteration added to count the initial iterati…^[14]에

바이너리 검색은 비교를 통한 검색을 위한 최적의 알고리즘이므로, 이 문제는 $다음$과 동일한 n ${\displaystyle n}$ 노드를$$ 가진 모든 바이너리 트리의 최소 내부 경로 길이를 계산하는 것으로 감소한다.^[17]

${\displaystyle I(n)=\sum _{k=1}^{n}\왼쪽\lfloor \log_{2}(k)\오른쪽\rfloor }$

예를 들어, 7-Element 배열에서 루트에는 1회의 반복이 필요하며, 루트 아래의 2개의 원소는 2회의 반복이 필요하며, 아래의 4개의 원소는 3회의 반복이 필요하다.이 경우 내부 경로 길이는 다음과 같다.^[17]

${\displaystyle \sum \{k=1}^{7}\왼쪽\lfloor \log_{2}(k)\right\bloor =0+2(1)+4(2)=2+8=10}$

평균 반복 횟수는 평균 사례에 대한 방정식을 기준으로$$ $1{\displaystyle \mathrm{}}$+ ${\displaystyle \frac{10}{}}$ 7${\displaystyle }$= 2 ${\displaystyle \frac{3}{}}$ ${\displaystyle 7\frac{\mathrm{}}{}}$ ${\$이 된다.$I{\displaystyle }$(${\displaystyle n}$) ${\displaystyle I(n)}$의 합은 다음과 같이 단순화할 수 있다$$.^[14]

${\displaystyle I(n)=\sum _{k=1}^{n}\left\lfloor \log _{2}(k)\right\rfloor =(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2}$

$I{\displaystyle }$( ${\displaystyle n}$) ${\displaystyle I(n)}$에 대한 방정식을 $T{\displaystyle }$( ${\displaystyle n}$) ${\displaystyle T(n)}$에 대한 방정식으로 대체하는 방법$:$^[14]

${\displaystyle T(n)=1+{\frac {(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2}{n}}=\lfloor \log _{2}(n)\rfloor +1-(2^{\lfloor \log _{2}(n)\rfloor +1}-\lfloor \log _{2}(n)\rfloor -2)/n}$

정수 $n{\displaystyle }$ ${\displaystyle n}$의 경우$,$ 이는 위에서 지정한 성공적인 검색에서 평균 대소문자를 나타내는 방정식과 동일하다.

검색 실패

실패한 검색은 확장된 이진 트리를 구성하는 외부 노드로 트리를 증가시킴으로써 나타낼 수 있다.내부 노드 또는 트리에 있는 노드가 2개 미만의 하위 노드를 가진 경우, 외부 노드라고 하는 하위 노드를 추가하여 각 내부 노드에는 하위 노드가 2개씩 있게 한다.그렇게 함으로써 실패한 검색은 마지막 반복 동안 남아 있는 단일 요소인 외부 노드에 대한 경로로 나타낼 수 있다.외부 경로는 루트에서 외부 노드로의 경로다.외부 경로 길이는 모든 고유 외부 경로의 길이를 합한 값이다.If there are ${\displaystyle n}$ elements, which is a positive integer, and the external path length is ${\displaystyle E(n)}$, then the average number of iterations for an unsuccessful search ${\displaystyle T'(n)={\frac {E(n)}{n+1}}}$, with the one iteration added to count the initi반복의어레이 요소 사이의 $간격$을 나타내는 $n{\displaystyle }$+ ${\displaystyle 1}$ ${\displaystyle$ n+1}의$$외부$$ 경로가 있기 때문에$$ 외부 경로 길이는 $n{\displaystyle }$${\displaystyle n}$이(가)^[14] ${\displaystyle \mathrm{아닌}}$n + 1 {\$displaystyle$ n+1}로 $나눈다$$.$

이 문제는 $비슷하게{\displaystyle }$ n ${\displaystyle n}$개의$$ 노드를 가진 모든 이진 트리의 최소 외부 경로 길이를 결정하는 것으로 줄일 수 있다.모든 이진 트리에 대해 외부 경로 길이는 내부 경로 길이 + ${\displaystyle \mathrm{2n}}$ ${\displaystyle 2n}$과 동일함.$$^[17]$I{\displaystyle }$(${\displaystyle n}$) ${\displaystyle I(n)}$에 대한 방정식 대체$:$^[14]

${\displaystyle E(n)=I(n)+2n=\left[(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2\right]+2n=(n+1)(\lfloor \log _{2}(n)\rfloor +2)-2^{\lfloor \log _{2}(n)\rfloor +1}}$

$E{\displaystyle }$( ${\displaystyle n}$) ${\displaystyle E(n)}$의 방정식을 $T$ ${\displaystyle {\prime }^{}}$(${\displaystyle n}$ ${\displaystyle )}$ ${\displaystyle$ T$'(n)}$의 방정식으로 대체하면 실패한 검색의 평균 사례를 확인할 수 있다$.$^[14]

${\displaystyle T'(n)={\frac {(n+1)(\lfloor \log _{2}(n)\rfloor +2)-2^{\lfloor \log _{2}(n)\rfloor +1}}{(n+1)}}=\lfloor \log _{2}(n)\rfloor +2-2^{\lfloor \log _{2}(n)\rfloor +1}/(n+1)}$

대체절차의 성과

위에서 정의한 바이너리 검색 절차의 각 반복은 중간 요소가 각 반복에서 목표값과 동일한지 여부를 확인하면서 한두 가지 비교를 한다.각 원소가 동등하게 검색될 가능성이 있다고 가정하면, 각 반복은 평균 1.5 비교를 한다.알고리즘의 변동은 중간 요소가 검색 끝에 있는 목표값과 동일한지 여부를 점검한다.평균적으로, 이것은 각 반복에서 반을 비교하는 것을 없앤다.이것은 대부분의 컴퓨터에서 반복적으로 걸리는 시간을 약간 줄인다.그러나 검색에는 최대 반복 횟수가 소요되며, 평균적으로 검색에 1회 반복이 추가된다.비교 루프는 최악의 경우 $\lfloor$ ${\mathrm{로그}}_{}$ ${2\mathrm{}}_{}$ ${}_{}$ $(n$)$$+ $1$ $\rfloor$ $(\textstyle \lfloor \log_{2}(n)+1\rfloor }$번만$$ 수행되므로 반복당 효율이 약간 증가해도 매우 큰 $n$ ${\textstyle n}$을 제외한 모든 경우에 추가 반복을 보상하지는 않는다$.$^[c][18][19]

실행 시간 및 캐시 사용

바이너리 검색의 성능을 분석함에 있어서, 또 다른 고려사항은 두 요소를 비교하는 데 필요한 시간이다.정수와 문자열의 경우 요소의 인코딩 길이(대개 비트 수)가 증가함에 따라 필요한 시간이 선형적으로 증가한다.예를 들어 64비트 비호환 정수의 쌍을 비교하려면 32비트 비호환 정수의 쌍을 비교할 때 비트를 두 배까지 비교해야 한다.정수가 같을 때 최악의 경우를 이룬다.이것은 큰 정수형이나 긴 문자열과 같이 요소의 인코딩 길이가 클 때 유의할 수 있으며, 이것은 요소 비교를 비싸게 만든다.더욱이 부동 소수점 값(실수의 가장 일반적인 디지털 표현)을 비교하는 것은 정수나 짧은 문자열을 비교하는 것보다 비용이 더 많이 드는 경우가 많다.

대부분의 컴퓨터 아키텍처에서 프로세서는 RAM과 별개의 하드웨어 캐시를 가지고 있다.그것들은 프로세서 자체 내에 위치하기 때문에, 캐시는 접근하기 훨씬 빠르지만 보통 RAM보다 훨씬 적은 데이터를 저장한다.따라서 대부분의 프로세서는 근래에 액세스한 메모리 위치와 함께 그것에 가까운 메모리 위치를 저장한다.예를 들어 어레이 요소에 액세스할 때 요소 자체를 RAM에 가깝게 저장한 요소와 함께 저장할 수 있어 인덱스가 서로 가까운 어레이 요소(참조 위치)에 순차적으로 액세스하는 속도가 빨라진다.정렬된 배열에서 바이너리 검색은 요소에 순차적으로 액세스하는 알고리즘(해시 테이블의 선형 검색, 선형 검색 등)과 달리 배열이 크면 원거리 메모리 위치로 점프할 수 있다.이는 대부분의 시스템에서 대형 어레이를 바이너리 검색하는 실행 시간을 약간 더한다.^[20]

이진 검색 대 다른 구성표

바이너리 검색이 포함된 정렬된 배열은 삽입 및 삭제 작업이 검색과 상호 저장될 때 각 작업에 대해 O$(n$) ${\textstyle O(n)}$시간이$$ 소요될 때 매우 비효율적인 솔루션이다.또한 정렬된 배열은 특히 요소가 배열로 삽입되는 경우가 많을 때 메모리 사용을 복잡하게 만들 수 있다.^[21]훨씬 더 효율적인 삽입과 삭제를 지원하는 다른 데이터 구조도 있다.바이너리 검색은 정확한 일치를 수행하고 멤버십을 설정하는 데 사용될 수 있다(대상 값이 값 집합에 있는지 여부 결정).더 빠른 정확한 일치를 지원하고 멤버십을 설정하는 데이터 구조가 있다.그러나 다른 많은 검색 방식과는 달리, 이진수 검색은 효율적인 근사 일치를 위해 사용될 수 있으며, 일반적으로 값 자체의 유형이나 구조에 관계없이 $O(\log$ $){\textstyle O(\log n)}$시간에$$ 그러한 일치를 수행할 수 있다.^[22]또한, 정렬된 배열에서 효율적으로 수행될 수 있는 가장 작은 요소와 가장 큰 요소 찾기 등의 작업이 있다.^[11]

선형검색

선형검색(Linear search)은 목표값을 찾을 때까지 모든 기록을 확인하는 간단한 검색 알고리즘이다.링크된 목록에서 선형 검색을 수행할 수 있어 배열보다 삽입 및 삭제 속도가 빠를 수 있다.바이너리 검색은 배열의 사전 정렬이 필요하지만 배열의 길이가 짧은 경우를 제외하고 정렬된 배열의 선형 검색보다 빠르다.^[d][24]퀵소트 및 병합 정렬과 같은 요소 비교에 기반한 모든 정렬 알고리즘은 최악의 경우 최소 $O(n$ $\log$ $n$) ${\textstyle O(n\log$ n$)}$ 비교가$$ 필요하다.^[25]선형 검색과 달리 바이너리 검색은 효율적인 근사 일치를 위해 사용할 수 있다.정렬된 배열에서 효율적으로 수행할 수 있지만 정렬되지 않은 배열에서는 수행할 수 없는 가장 작고 큰 요소를 찾는 등의 작업이 있다.^[26]

나무들

바이너리 검색 트리는 바이너리 검색 원리에 따라 작동하는 바이너리 트리 데이터 구조다.트리의 기록은 정렬된 순서대로 배열되며, 트리의 각 레코드는 평균 로그 시간을 잡아 이진 검색과 유사한 알고리즘을 사용하여 검색할 수 있다.또한 삽입과 삭제에는 이진 검색 트리의 평균 로그 시간이 필요하다.이는 정렬된 배열의 선형 시간 삽입 및 삭제보다 빠를 수 있으며, 이진 트리는 범위와 대략적인 질의를 포함하여 정렬된 배열에서 가능한 모든 작업을 수행할 수 있는 능력을 유지한다.^[22][27]

그러나 바이너리 검색 트리가 불완전하게 균형을 이룰 가능성이 높기 때문에 바이너리 검색은 보통 검색에 더 효율적이다.이것은 균형 잡힌 이진 검색 트리, 즉 그들 자신의 노드의 균형을 유지하는 이진 검색 트리에도 적용된다. 왜냐하면 그들은 가능한 가장 적은 레벨의 트리를 거의 생산하지 않기 때문이다.균형 잡힌 이진 검색 트리를 제외하고, 트리는 두 개의 자식 노드가 있는 내부 노드가 거의 없이 심하게 불균형되어 평균 검색 시간과 최악의 경우 검색 시간이 $n$ ${\textstylen}$ 비교에$$ 근접할 수 있다.^[e]이진 검색 트리는 정렬된 배열보다 더 많은 공간을 차지한다.^[29]

바이너리 검색 트리는 파일 시스템에서 효율적으로 구조화할 수 있기 때문에 하드 디스크에 저장된 외부 메모리에서 빠른 검색을 할 수 있다.B 트리는 이 나무 조직 방법을 일반화한다.B-tree는 데이터베이스나 파일 시스템 같은 장기 저장소를 구성하는 데 자주 사용된다.^[30][31]

해싱

연관 배열을 구현하기 위해서는 일반적으로 해시함수를 사용하여 키를 레코드에 매핑하는 데이터 구조인 해시 테이블이 정렬된 레코드 배열에서 이진 검색보다 빠르다.^[32]대부분의 해시 테이블 구현은 평균적으로 상각된 일정 시간만 필요로 한다.^[f][34]그러나 해싱은 검색 실패에 대한 유일한 정보가 어떤 기록에도 대상이 존재하지 않는다는 것이므로 가장 작은 키, 다음으로 큰 키, 가장 가까운 키를 계산하는 것과 같은 대략적인 일치에는 유용하지 않다.^[35]바이너리 검색은 로그타임으로 수행하는 이러한 일치 항목에 이상적이다.바이너리 검색도 대략적인 일치사항을 지원한다.가장 작은 요소와 가장 큰 요소 찾기 같은 일부 작업은 해시 테이블이 아닌 정렬된 배열에서 효율적으로 수행될 수 있다.^[22]

구성원 자격 알고리즘 설정

검색과 관련된 문제는 멤버십 설정이다.이진 검색과 같이 룩업을 하는 모든 알고리즘은 설정된 멤버쉽에도 사용될 수 있다.세트 멤버십에 보다 구체적으로 적합한 다른 알고리즘이 있다.비트 배열은 키의 범위가 제한되었을 때 가장 간단하고 유용하다.그것은 비트의 컬렉션을 콤팩트하게 저장하며, 각 비트는 키의 범위 내에서 하나의 키를 나타낸다.비트 배열은 매우 빠르며$O$ ($1$ ) ${\textstyle O$(1) $시간$만 소요된다.^[36]Judy1 타입의 Judy 어레이는 64비트 키를 효율적으로 처리한다.^[37]

대략적인 결과를 위해, 해싱을 기반으로 하는 또 다른 확률론적 데이터 구조인 블룸 필터는 비트 배열과 다중 해시 함수를 사용하여 키를 인코딩하여 키 집합을 저장한다.블룸 필터는 대부분의 경우 비트 배열보다 공간 효율성이 훨씬 뛰어나며 $그다지$ 느리지 않다$.$ k {\$textstyle$ k$}$ 해시$$ 함수를 사용할 경우 구성원 쿼리에는 $O$( $k$) ${\textstyle O(k)}$시간만$$ 필요하다.그러나 Bloom 필터는 잘못된 긍정으로 고통받는다.^[g][h][39]

기타 데이터 구조

정렬된 배열에서 사용할 수 있는 검색 및 기타 작업 모두에 대해 경우에 따라 바이너리 검색을 개선할 수 있는 데이터 구조가 존재한다.예를 들어, 반 엠드 보아스 트리, 퓨전 트리, 시도 및 비트 배열과 같은 전문 데이터 구조에서 바이너리 검색보다 정렬된 배열에서 사용할 수 있는 검색, 대략적인 일치 및 작업을 더 효율적으로 수행할 수 있다.이러한 전문화된 데이터 구조는 특정 속성(대개 작은 정수인 키)을 가진 키의 속성을 이용하기 때문에 대개 더 빠를 뿐이며, 따라서 그러한 속성이 부족한 키에 시간이나 공간을 소비하게 된다.^[22]키를 주문할 수 있는 한, 이러한 작업은 항상 키와 상관없이 정렬된 배열에서 최소한 효율적으로 수행될 수 있다.Judy 어레이와 같은 일부 구조는 효율성과 대략적인 일치를 수행할 수 있는 능력을 유지하면서 이를 완화하기 위해 접근방식을 조합하여 사용한다.^[37]

변형

균일 이진 검색

균일한 이진 검색 저장소는 하한 및 상한 대신 현재 반복에서 다음 반복까지의 중간 요소 인덱스 차이.차이점을 포함하는 조회표는 사전에 계산된다.예를 들어 검색할 배열이 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]인 경우 중간 요소(${\displaystyle }$ ${\displaystyle m$는 6이 된다.이 경우 왼쪽 서브 어레이의 중간 요소([1, 2, 3, 4, 5])는 3이고 오른쪽 서브 어레이의 중간 요소([7, 8, 9, 10, 11])는 9이다.균일한 이항 검색은 두 지수 모두 같은 양으로 6과 다르기 때문에 3의 값을 저장할 것이다.^[40]검색 공간을 줄이기 위해 알고리즘은 중간 요소의 인덱스에서 이 변경 사항을 추가하거나 뺀다.균일한 이진 검색은 십진수 컴퓨터와 같이 중간점을 계산하는 것이 비효율적인 시스템에서 더 빠를 수 있다.^[41]

지수 검색

지수 검색은 이진 검색을 바인딩되지 않은 목록으로 확장한다.그것은 두 개의 검정력이면서 목표값보다 큰 지수를 가진 첫 번째 요소를 찾는 것으로 시작한다.이후 해당 인덱스를 상한으로 설정하고 이진 검색으로 전환한다.A search takes ${\textstyle \lfloor \log _{2}x+1\rfloor }$ iterations before binary search is started and at most ${\textstyle \lfloor \log _{2}x\rfloor }$ iterations of the binary search, where ${\textstyle x}$ is the position of the target value.지수 검색은 경계 리스트에서 작동하지만, 대상 값이 배열 시작 부근에 있는 경우에만 이진 검색에 비해 개선된다.^[42]

보간검색

보간 검색은 중간점을 계산하는 대신 배열의 길이뿐 아니라 배열에서 가장 낮고 가장 높은 요소도 고려하여 목표값의 위치를 추정한다.그것은 중간점이 많은 경우에 가장 좋은 추측이 아니라는 것을 근거로 작용한다.예를 들어, 목표값이 배열에서 가장 높은 요소에 가까우면 배열 끝 근처에 위치할 가능성이 높다.^[43]

일반적인 보간 함수는 선형 보간이다.If ${\displaystyle A}$ is the array, ${\displaystyle L,R}$ are the lower and upper bounds respectively, and ${\displaystyle T}$ is the target, then the target is estimated to be about ${\displaystyle (T-A_{L})/(A_{R}-A_{L})}$ of the way between ${\displaystyle L}$및 $R{\displaystyle }$ ${\displaystyle R$ 선형 보간이 사용되고 배열 요소의 분포가 균일하거나 거의 균일할 경우 보간 검색은 $O(\log$log $\log \mathrm{logn}$ )${\textstyle O(\log \log$ n$)}$을(를) 비교한다$$.^[43][44][45]

실제로 보간 검색은 보간 검색에 추가 계산이 필요하기 때문에 작은 배열의 이진 검색보다 속도가 느리다.그것의 시간 복잡성은 이진 검색보다 더 느리게 증가하지만, 이것은 큰 배열을 위한 여분의 계산만을 보상한다.^[43]

분수 계단식

분수 계단식 배열은 여러 정렬 배열에서 동일한 요소에 대한 이진 검색 속도를 높이는 기법이다.각 어레이를 개별적으로 검색하려면 $O(k$ $\log$ $n$) ${\textstyle O(k\log$ n$)}$ 시간이$$ 필요하며 여기서 $k$ ${\textstyle k}$은 어레이 수입니다.분수 계단식 계단식 배열은 각 요소와 다른 배열의 해당 위치에 대한 특정 정보를 각 배열로 저장함으로써$이$를 O$(k$ + $\log )n$ )$${\$textstyle O($k+\$log$ n$)}($으)로 줄인다.^[46][47]

프랙탈 캐스캐이딩은 원래 다양한 연산 기하학 문제를 효율적으로 해결하기 위해 개발되었다.데이터 마이닝과 인터넷 프로토콜 라우팅과 같은 다른 곳에서는 소수점 계단식 작업이 적용되었다.^[46]

그래프로 일반화

이항 검색은 특정 유형의 그래프에서 작동하도록 일반화되었으며, 대상 값은 배열 요소 대신 꼭지점에 저장된다.이진 검색 트리는 그러한 일반화 중 하나이다. 즉, 트리의 꼭지점(노드)이 쿼리될 때, 알고리즘은 정점이 대상이라는 것을 학습하거나, 그렇지 않으면 대상이 위치하는 하위 트리를 학습한다.단, 이는 다음과 같이 더욱 일반화될 수 있다: 방향성이 없고 양의 가중 그래프와 목표 정점을 주어진다면, 알고리즘은 정점을 쿼리할 때 그것이 목표와 동일하다는 것을 배우거나, 또는 쿼리 정점에서 목표물에 이르는 최단 경로에 있는 입사 에지가 주어진다.표준 바이너리 검색 알고리즘은 단순히 그래프가 경로인 경우다.마찬가지로, 이진 검색 트리는 조회된 정점이 대상과 동일하지 않을 때 왼쪽 또는 오른쪽 하위 트리의 가장자리가 주어지는 경우다.모든 비방향 양의 가중치 그래프의 경우 최악의 경우 $O{\displaystyle }$(log ${\displaystyle (n}$ )${\displaystyle$ O$(\log n)$ 쿼리에서 목표 정점을$$ 찾는 알고리즘이 있다.^[48]

노이즈가 많은 이진 검색

노이즈가 많은 바이너리 검색 알고리즘은 알고리즘이 어레이의 요소를 신뢰성 있게 비교할 수 없는 경우를 해결한다.각 요소 쌍에 대해 알고리즘이 잘못된 비교를 할 가능성이 있다.소음이 많은 이항 검색은 양보된 위치의 신뢰성을 제어하는 주어진 확률로 대상의 정확한 위치를 찾을 수 있다.Every noisy binary search procedure must make at least ${\displaystyle (1-\tau ){\frac {\log _{2}(n)}{H(p)}}-{\frac {10}{H(p)}}}$ comparisons on average, where ${\displaystyle H(p)=-p\log _{2}(p)-(1-p)\log _{2$$}(1-p)}$은 이항 엔트로피 함수이고 $\tau {\displaystyle }$ ${\displaystyle \tau }$은 절차가 잘못된 위치를 산출할 확률이다$$.^[49][50][51]시끄러운 바이너리 검색 문제는 답이 틀릴 수 있는 스무 개의 질문의 변종인 ^[52]레니-울람 게임의 사례로 볼 수 있다.^[53]

양자 이진 검색

클래식 컴퓨터는 바이너리 검색을 수행할 때 정확히 $\lfloor$ ${\mathrm{로그}}_{}$ ${2\mathrm{}}_{}\mathrm{2n}$+ $1$ $\rfloor$ ${\textstyle \lfloor \log_{2}n+1\rfloor }$번$$ 반복하는 최악의 경우에 한정된다.이진 검색을 위한 양자 알고리즘은 여전히 ${\mathrm{로그}}_{}$ ${2\mathrm{}}_{}\mathrm{2n}$ ${\textstyle \log _{2}n}$ 쿼리$$(고전 절차의 반복을 나타냄)의 비율로 제한되지만 상수 요인은 1보다 작기 때문에 양자 컴퓨터의 시간 복잡성을 줄일 수 있다.Any exact quantum binary search procedure—that is, a procedure that always yields the correct result—requires at least ${\textstyle {\frac {1}{\pi }}(\ln n-1)\approx 0.22\log _{2}n}$ queries in the worst case, where ${\textstyle \ln }$ is the natural logarithm.^[54]최악의 경우 $4\mathrm{}$ ${\log }_{}$ ${605}_{}$ ${}_{}$ $n43$ 0.${\mathrm{433}}_{}$ log ${2\mathrm{}}_{}$ ${}_{}$ $n${\$textstyle$ 4$\log _{$605}$n\ 약$0$.433\log_{$2}$n}$ 쿼리에서$$ 실행되는 정확한 양자 이진 검색 절차가 있다.^[55]이에 비해 그로버 알고리즘은 정렬되지 않은 요소 리스트를 검색하기 위한 최적의 양자 알고리즘으로, $O{\displaystyle (n}$) ${\displaystyle O({\sqrt{n}})$ 쿼리가$$ 필요하다.^[56]

역사

더 빠른 검색을 위해 품목 리스트를 분류하는 아이디어는 옛날로 거슬러 올라간다.가장 먼저 알려진 예는 기원전 200년 전의 바빌로니아의 이나키빗-아누 판이다.이 태블릿에는 약 500개의 성소수 숫자와 이들의 답례문이 사전순으로 정렬되어 있어 특정 항목을 더 쉽게 찾을 수 있었다.또, 첫 글자로 분류한 여러 명의 이름 목록이 에게 해 제도에서 발견되었다.1286년 CE에 완성된 라틴어 사전인 카톨리콘은 처음 몇 글자만이 아니라 단어들을 알파벳순으로 분류하는 규칙을 기술한 최초의 작품이었다.^[9]

1946년 존 모클리는 컴퓨터 분야의 핵심 대학 과정인 무어 학교 강의의 일부로 이진수색에 대한 첫 언급을 했다.^[9]1957년 윌리엄 웨슬리 피터슨은 보간검색을 위한 첫 번째 방법을 발표했다.^[9][57]발표된 모든 이진 검색 알고리즘은 데릭 헨리 레머가 모든 배열에서 작동하는 이진 검색 알고리즘을 발표하기 전까지 길이가 2의^[i] 힘보다 1보다 작은 배열에서만 작동했다.^[59]1962년 헤르만 보텐브루흐는 평등을 위한 비교를 마지막에 배치한 2진수 검색의 ALGOL 60 구현을 제시하여 평균 반복 횟수를 1회 증가시키지만 반복당 비교 횟수는 1회로 축소하였다.^[8]균일한 이항 검색은 1971년 스탠포드 대학의 A. K. Chandra에 의해 개발되었다.^[9]1986년 베르나르 샤젤과 레오니다스 J. 기바스는 컴퓨터 기하학에서 수많은 검색 문제를 해결하기 위한 방법으로 분수계 캐스케이딩을 도입했다.^[46][60][61]

구현 문제

바이너리 검색의 기본이념은 비교적 간단하지만, 디테일은 의외로 까다로울 수 있다.

— Donald Knuth^[2]

존 벤틀리가 전문 프로그래머들을 위한 과정에서 바이너리 검색을 문제로 지정했을 때, 그는 90%가 몇 시간 동안 작업을 한 후 정확한 해결책을 제시하지 못했다는 것을 발견했는데, 주로 잘못된 구현이 실행되지 못하거나 드문 경우에서 오답을 반환했기 때문이다.^[62]1988년에 출판된 한 연구는 그것에 대한 정확한 코드가 20개의 교과서 중 5개에서만 발견된다는 것을 보여준다.^[63]더욱이 벤틀리가 1986년 저서 '프로그래밍 진주(Programming Pearls)'에 발표한 바이너리 검색의 자체 시행에는 20년 넘게 발견되지 않은 오버플로 오류가 담겨 있었다.이진 검색의 자바 프로그래밍 언어 라이브러리 구현은 9년 이상 동일한 오버플로 버그를 가지고 있었다.^[64]

실제 구현에서 지수를 나타내기 위해 사용되는 변수는 종종 고정 크기(정수)가 될 것이며, 이는 매우 큰 배열의 산술 오버플로를 초래할 수 있다.$스팬$의 중간점이 $L{\displaystyle \frac{}{}}$$$+ ${\displaystyle \frac{\mathrm{}}{}}$ 2 ${\$ L + ${\displaystyle R}$ ${\$$displaystyle L}$과 R ${\displaystyle R}$ 범위에 있더라도$$ $L{\displaystyle }$+ R {\displaystystyle R$}$의 값이 중간점 저장에 사용되는 데이터 유형의 정수 범위를 초과할 수 있다$$.$L{\displaystyle }$ ${\displaystyle L}$ $및$ R ${\displaystyle R}$이(가) 음이 아닌 경우 중간점을 $L{\displaystyle }$+ ${\displaystyle R\frac{}{}}$- ${\displaystyle \frac{L}{}}$ ${\displaystyle \frac{\mathrm{}}{}}$ ${\$}}로 계산하면 이를 방지할 수 있다$.$^[65]

무한 루프에 대한 출구 조건이 올바르게 정의되지 않은 경우 무한 루프가 발생할 수 있다.$L{\displaystyle }$ ${\displaystyle L}$이$($가) $R{\displaystyle }$ ${\displaystyle R}$을(를) 초과하면 검색이 실패했으며 검색 실패를 전달해야 한다.또한 대상 요소가 발견되었을 때 루프를 빼야 하거나, 이 점검이 끝까지 옮겨지는 구현의 경우, 마지막에 검색이 성공했는지 실패했는지 여부를 확인해야 한다.벤틀리는 바이너리 검색을 잘못 시행한 프로그래머 대부분이 출구 조건을 규정하는 과정에서 오류를 범했다는 사실을 발견했다.^[8][66]

도서관 지원

많은 언어의 표준 라이브러리에는 이진 검색 루틴이 포함된다.

• C는 기능을 제공한다. bsearch()공식 표준이 그렇게 요구하지는 않지만, 일반적으로 바이너리 검색을 통해 구현되는 표준 라이브러리에.^[67]
• 기능을 제공하는 C++의 표준 템플릿 라이브러리binary_search(),lower_bound(),upper_bound()그리고equal_range().^[68]
• D의 표준 도서관 Phobos, instd.range모듈은 유형을 제공한다.SortedRange(에 의해 결정됨sort()그리고assumeSorted()함수) 방법 포함contains(),equaleRange(),lowerBound()그리고trisect()임의 액세스를 제공하는 범위에 대해 기본적으로 이진 검색 기술을 사용하는 ^[69].
• COBOL은 다음을 제공한다.SEARCH ALLCOBOL 순서 테이블에서 이진 검색을 수행하기 위한 동사.^[70]
• 고즈sort표준 라이브러리 패키지에는 기능이 포함되어 있음Search,SearchInts,SearchFloat64s그리고SearchStrings일반 바이너리 검색뿐만 아니라 각각 정수 조각, 부동 소수점 번호 및 문자열 검색을 위한 특정 구현도 구현한다.^[71]
• Java는 오버로드된 일련의 기능을 제공한다. binarySearch()수업의 정적 방법.Arrays그리고Collections표준으로java.utilJava 어레이 및 온라인에서 이진 검색을 수행하는 패키지Lists,^[72][73] 각각
• 마이크로소프트의NET Framework 2.0은 수집 기본 클래스에서 이진 검색 알고리즘의 정적 일반 버전을 제공한다.예를 들면 다음과 같다.System.Array의 방법BinarySearch<T>(T[] array, T value).^[74]
• Objective-C의 경우, 코코아 프레임워크는 다음을 제공한다.NSArray -indexOfObject:inSortedRange:options:usingComparator:Mac OS X 10.6+^[75]의 방법.애플의 Core Foundation C 프레임워크에도 다음과 같은 내용이 포함되어 있다.CFArrayBSearchValues()기능을 ^[76]발휘하다
• Python이 제공하는 것은bisect모듈.^[77]
• Ruby's Array 클래스에는bsearch대략적인 일치가 내장된 방법.^[78]

참고 항목

• 이분법 - 함수의 0을 찾기 위한 알고리즘 - 실제 숫자의 방정식을 푸는 데 사용된 것과 동일한 아이디어
• 곱하기 이항 검색 – 단순화된 중간점 계산으로 이항 검색 변동

참고 및 참조

이 기사는 2018년 외부 학술 동료 검토를 위해 위키저널 사이언스지에 제출되었다(검토자 보고서).업데이트된 콘텐츠는 CC-BY-SA-3.0 라이센스(2019)에 따라 위키백과 페이지로 다시 통합되었다.검토된 기록의 버전은 다음과 같다."Binary search algorithm" (PDF). WikiJournal of Science. 2 (1): 5. 2 July 2019. doi:10.15347/WJS/2019.005. ISSN 2470-6345. Wikidata Q81434400.

메모들

인용구

원천

외부 링크

Wikibook 알고리즘 구현에 다음 주제의 페이지가 있음: 바이너리 검색

• NIST 알고리즘 및 데이터 구조 사전: 이진 검색
• C에서 다양한 바이너리 검색 구현에 대한 비교 및 벤치마크