최대 균일성
Maximal evenness
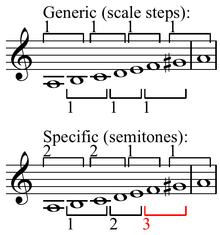
척도(음악) 이론에서, 최대 고른 설정(척도)은 모든 일반 간격에 특정한 한 두 개의 연속적인 정수를 갖는 것, 즉 음표(pcs)가 "가능한 한 많이 펼쳐지는" 척도를 말한다.이 재산은 처음에 존 클로우와 잭 도트트에 의해 설명되었다.[1]클로우와 도트도 최대한 짝수 알고리즘을 도입했다.색도 카디널리티 c와 pc세트 카디널리티 d의 경우 최대 짝수 세트가
여기서 k의 범위는 0 ~ d - 1과 m이며, 0 ≤ m ≤ c - 1은 고정되어 있으며, 브래킷 쌍은 바닥 기능이다.이러한 개념에 대한 논의는 이음계 이론의 수학적 기초에 관한 티모시 존슨의 저서에서 찾을 수 있다.[2]잭 더트와 리차드 크랜츠는 수학 문학에 대한 세트까지 최대로 소개했다.[3][4]
하나의 척도는 모든 일반적 간격이 두 개의 특정 간격 크기로 나오면 마이힐의 속성을 갖는다고 하며, 마이힐의 속성을 가진 척도는 잘 형성된 척도라고 한다.[5]이음계 수집은 둘 다 잘 형성된 저울이며 최대 균일하다.홀톤 음계도 최대 고른 편이지만, 일반 간격마다 한 가지 크기만 나오기 때문에 모양이 좋지 않다.
2차 순서의 최대 균일성은 최대 균일성을 갖는 더 큰 집합의 하위 집합의 최대 균일성이다.디아토닉 트라이애드와 일곱 번째 화음은 최대 고른 디아토닉 스케일에 관해서도 최대 고른 2차 음률을 가지고 있지만, 색도 스케일에 관해서도 최대 고른 것은 아니다.(ibid, p.115) 이 내포된 품질은 아래에서 위로 피치 공간을 위한 Fred Lerdahl의 "축소 형식"과[6] 유사하다.
| C | E | G | C | |||||||||
| C | D | E | F | G | A | B | C | |||||
| C | D♭ | D | E♭ | E | F | F♯ | G | A♭ | A | B♭ | B | C |
- (Lerdahl, 1992년)
역동적인 접근 방식에서는 회전하는 동심원과 최대 반복적으로 짝수 세트가 구성되었다.이 접근법은 신-리만 이론에 함축되어 있으며, 이음계 이론과 색채 이론 사이의 흥미로운 연결로 이어진다.[7]에마뉘엘 아미오트는 분리된 푸리에 변환을 사용함으로써 고른 집합을 최대화 할 수 있는 또 다른 방법을 발견했다.[8][9]
캐리, 노먼, 클램핏, 데이비드(1989년)."잘 형성된 저울의 전망" 음악 이론 스펙트럼 11: 187–206.
참조
- ^ Clough, John; Douthett, Jack (1991). "Maximally Even Sets". Journal of Music Theory (35): 93-173.
- ^ Johnson, Timothy (2003). Foundations of Diatonic Theory: A Mathematical Based Approach to Musical Fundamentals. Key College Publishing. ISBN 1-930190-80-8.
- ^ Douthett, Jack; Krantz, Richard (2007). "Maximally Even Sets and Configurations: Common Threads in Mathematics, Physics and Music". Journal of Combinatorial Optimization. 14: 385-410.
- ^ Douthett, Jack; Krantz, Richard (2007). "Dinner Tables and Concentric Circles: A harmony of Mathematics, Music, and Physics". College Mathematics Journal. 39 (3): 203-211.
- ^ Carey, Norman; Clampitt, David (1989). "Aspects of Well-Formed Scales". Music Theory Spectrum. 11: 187-206.
- ^ Lerdahl, Fred (1992). "Cognitive Constraints on Compositional Systems". Contemporary Music Review. 6 (2): 97-121.
- ^ Douthett, Jack (2008). "Filter Point-Symmetry and Dynamical Voice-Leading". Music and Mathematics:Chords, Collections, and Transformations. Eastman Studies in Music: 72-106. Ed. J. Douthett, M. Hyde, and C. Smith. University of Rochester Press, NY. ISBN 1-58046-266-9
- ^ Armiot, Emmanuel (2007). "David Lewin and Maximally Even Sets". Journal of Mathematics and Music. 1 (3): 157-172.
- ^ Armiot, Emmanuel (2016). Music Through Fourier Space: Discrete Fourier Transform in Music Theory. Springer. ISBN 9783319455808.