병합 알고리즘

병합 알고리즘은 여러 개의 정렬된 목록을 입력으로 가져가고 단일 목록을 출력하는 알고리즘 계열로, 입력 목록의 모든 요소를 정렬된 순서로 포함하고 있다. 이러한 알고리즘은 다양한 정렬 알고리즘에서 서브루틴으로 사용되는데, 가장 유명한 것은 병합 정렬이다.

적용

병합 정렬 예제

병합 알고리즘은 비교 기반 정렬 알고리즘인 병합 정렬 알고리즘에서 중요한 역할을 한다. 개념적으로 병합 정렬 알고리즘은 다음 두 단계로 구성된다.

각 하위 목록에 요소가 하나만 포함될 때까지 목록을 같은 길이의 하위 목록으로 반복적으로 나누거나, 반복적으로(아래로 위로) 병합 정렬의 경우 n개 요소 목록을 크기 1의 하위 목록으로 고려하십시오. 단일 요소를 포함하는 목록은 정의에 따라 정렬된다.
단일 목록에 모든 요소가 포함될 때까지 하위 목록을 반복적으로 병합하여 새 정렬 하위 목록을 만드십시오. 단일 목록은 정렬된 목록이다.

병합 알고리즘은 병합 정렬 알고리즘에서 반복적으로 사용된다.

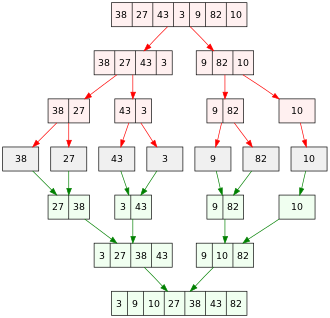
예제 병합 정렬은 그림에 나와 있다. 그것은 7개의 정수의 정렬되지 않은 배열로 시작한다. 배열은 7개의 파티션으로 나뉘며, 각 파티션은 1개의 요소를 포함하고 정렬된다. 그런 다음 정렬된 파티션은 병합되어 정렬된 배열인 하나의 파티션이 남아 있을 때까지 더 크고 정렬된 파티션을 생성한다.

두 목록 병합

정렬된 두 목록을 하나의 목록으로 병합하는 작업은 (데이터 액세스 모델에 따라) 선형 시간 및 선형 또는 상수 공간으로 수행할 수 있다. 다음의 유사코드는 입력 목록(연결 목록 또는 배열 중 $하나$ ) $A$ 와 B를 $새로운$ 목록 C에 병합하는 알고리즘을 보여준다.^[1]^[2]^{: 104} 함수 헤드는 목록의 첫 번째 요소를 산출한다. 요소는 일반적으로 포인터 또는 색인을 증가시켜 목록에서 제거하는 것을 의미한다.

알고리즘 병합(A, B)은 입력 A, B : 목록 C := 목록 C := 새로운 빈 목록으로 A가 비어 있지 않고 B가 비어 있지 않은 동안 HEAD(A) ≤ Head(B)를 C에 더하고, A에 HEAD(B)를 C에 추가하면 A 또는 B의 머리를 지금쯤이면 B //가 비어 있다. 다른 입력 목록을 비워야 한다. A가 비어 있지 않은 동안 C에 머리(A)를 추가하고 B가 비어 있지 않은 동안 머리(B)를 C에 추가한다.

입력이 링크된 목록일 때, 이 알고리즘은 일정한 양의 작업 공간만 사용하도록 구현될 수 있다; 목록 노드의 포인터는 부기 및 최종 병합 목록 구성에 재사용될 수 있다.

병합 정렬 알고리즘에서 이 서브루틴은 일반적으로 두 개의 하위 어레이 A[lo]를 병합하는 데 사용된다.mid], A[mid+1..단일 배열 A의 hi] 이것은 서브 아레이를 임시 배열로 복사한 다음 위의 병합 알고리즘을 적용하면 된다.^[1] 임시 배열을 할당하는 것은 피할 수 있지만 속도와 프로그래밍 용이성을 희생해야 한다. $다양$ 한 내부 병합 알고리즘이 고안되었으며, 때로는 O(^[3] $n$ $log$ $n)$ 알고리즘을 생성하기 위한 선형 시간 바인딩이 희생되기도 한다.^[4] 자세한 내용은 병합 정렬 § 변형을 참조하십시오.

K-way 병합

k-way 병합은 정렬된 입력 목록의 임의 번호 $k$ 에 대한 이진 병합 일반화. 인내심 sorting[5]고 k에 대한 입력을 나누는 외부 구분 알고리즘).mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{포함한 다양한 정렬 알고리즘에서 k-way 병합의 응용 프로그램은 올 때가 있습니다.디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{.국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1/M 가장 기억에 남는 것은 맞는 − 1블록, 종류 이 문제들을 하나씩 하나씩, 이 블록 합쳐진다.[2]:119–120

이 문제에 대한 몇 가지 해결책이 존재한다. 순진한 해결책은 매번 $최소$ 요소를 선택하기 위해 k 목록 위로 루프를 하고 모든 목록이 비워질 때까지 이 루프를 반복하는 것이다.

입력: k $목록$ .
목록이 비어 있지 않은 경우:
- 최소 첫 번째 요소가 있는 항목을 찾으려면 목록을 반복하십시오.
- 최소 요소를 출력하여 목록에서 제거하십시오.

최악의 경우 이 알고리즘은 ( $k-1)(n-k /$ 2 $)$ $요소$ 비교를 수행하여 목록에 총 $n개$ 의 요소가 있을 경우 작업을 수행한다.^[6] 목록을 첫 번째 요소로 키핑된 우선순위 대기열(min-heap)에 저장하여 개선할 수 있다.

$첫$ 번째 요소를 키로 사용하여 k 리스트의 최소 heap $h$ 를 작성한다.
목록이 비어 있지 않은 경우:
- Let $i = find-min(h)$ .
- 목록 $i$ 의 첫 번째 요소를 출력하고 목록에서 제거하십시오.
- $h$ 를 다시 가열한다.

출력될 다음으로 작은 요소(Find-min)를 검색하고 힙 순서를 복원하는 작업은 이제 $O (log$ $k)$ 시간(더 구체적으로는 $2⌊log$ $k ⌋$ 비교^[6])으로 할 수 있으며 전체 문제는 O( $n log$ k) $시간$ $($ 약 $2nlg k⌋$ 비교)으로 해결할 수 있다.^[6]^[2]^{: 119–120}

문제의 세 번째 알고리즘은 바이너리 병합 알고리즘을 기반으로 하는 분할 및 정복 솔루션이다.

$k$ = $1$ 이면 단일 입력 목록을 출력한다.
$k$ = $2$ 인 경우 이항 병합을 수행하십시오.
그렇지 않으면, 첫 번째 $kk /2$ lists 목록과 최종 $kk /2$ lists 목록을 재귀적으로 병합한 다음, 이진수가 이들을 병합한다.

이 알고리즘에 대한 입력 목록을 가장 짧은 길이 순으로 정렬할 경우 $n ⌈log$ $k ⌉$ 비교, 즉 힙 기반 알고리즘에 사용되는 수의 절반 미만이 필요하며, 실제로는 힙 기반 알고리즘만큼 빠르거나 느릴 수 있다.^[6]

병렬 병합

바이너리 병합 알고리즘의 병렬 버전은 병렬 병합 정렬의 구성 요소 역할을 할 수 있다. 다음의 유사 부호는 이 알고리즘을 병렬 분할 및 변환 스타일로 나타낸다(Cormen 등으로부터 추가).^[7]^{: 800} 두 $개$ 의 $정렬$ 된 배열 A와 B에서 작동하며, 정렬된 출력을 $배열$ C에 기록한다. 표기법 A[i...j]는 지수 $i$ 부터 $j$ 까지 $A$ 의 부분을 나타낸다.

알고리즘 병합(A[i...j], B[k...]ℓ], C[p...q]cm는 입력 A, B, C:배열 나는, j, k, ℓ, p, q:지수 알려 주m)j-명확히 설명, nxℓ-k만약 m<>n 다음 교환 A와 B을 끓여도록 확실히 하는 더 큰 배열:나는, j여전히의 자리로 A;k, ℓ A를 B에게 스왑 m와 엔 만약 m≤ 0그러면을 끓여기준이 전혀 없합병하자 r)⌊(나는 j+)/2⌋ s)binary-s.귀차(A[r], B[k]...)ℓ]) t = p + (r - i) + (s - k) C[t] = A[r]를 병렬로 병합을 실행(A[i...r], B[k...s], C[p...t]) 병합을 실행한다(A[r+1...j], B[s...ℓ, C[t+1...q])

알고리즘은 A $또는$ $B$ 중 더 큰 것을 (거의) 절반으로 나누어 작동한다. 그런 다음 다른 배열을 첫 번째 중간점보다 작은 값을 가진 부분과 더 크거나 같은 값을 가진 부분으로 분할한다. (이진 검색 서브루틴은 $A [r]$ 가 $B$ 인 경우 $B$ 의 인덱스를 반환하며, 이는 항상 $k$ 와 $ℓ$ 사이의 숫자임) 마지막으로 각 반쪽 쌍은 재귀적으로 병합되며, 재귀 호출은 서로 독립적이기 때문에 병행할 수 있다. 재귀 기반 사례에 직렬 알고리즘이 사용되는 하이브리드 접근방식은 실제적으로 우수한 성능을 발휘하는 것으로 입증되었다.

총 $n개$ 의 요소, 즉 그것의 직렬 버전의 가동 시간을 보유하는 두 개의 어레이에 대해 알고리즘에 의해 수행되는 작업은 O $(n$ )이다 $.$ $이것$ 은 n개의 원소를 $C$ 로 복사해야 하기 때문에 최적이다. 알고리즘의 범위를 계산하려면 Repeat(재발) 두 번의 재귀적 통화가 병행되기 때문에 두 통화의 비용만 고려할 필요가 있다. 최악의 경우, 요소가 더 많은 배열이 반으로 완벽하게 분할되기 때문에 ${\textstyle {\frac {3}{4}}n}$ 한 재귀 호출에서 최대 요소 수는 최대 ${\textstyle {\frac {3}{4}}n}$ ${\textstyle {\frac {3}{4}}n}$ ${\textstyle {\frac{3}{4}n}$ 이다. 이진 검색의 search(log $\Theta \left(\log(n)\right)$ ( $\Theta \left(\log(n)\right)$ ) ${\$ 비용을 $\Theta \left(\log(n)\right)$ 추가하면 다음과 같은 상한으로 반복이 반복된다.

$T_{\infully }^{\text{merge}(n)=T_{\\puty }^{\text{merge}\왼쪽({\frac {3}{4}n\오른쪽)+\theta \left(\log(n)\right)$

해결책은 $T_{\infty }^{\text{merge}}(n)=\Theta \left(\log(n)^{2}\right)$ $T_{\infty }^{\text{merge}}(n)=\Theta \left(\log(n)^{2}\right)$ $T_{\infty }^{\text{merge}}(n)=\Theta \left(\log(n)^{2}\right)$ ( $T_{\infty }^{\text{merge}}(n)=\Theta \left(\log(n)^{2}\right)$ ) $T_{\infty }^{\text{merge}}(n)=\Theta \left(\log(n)^{2}\right)$ = $T_{\infty }^{\text{merge}}(n)=\Theta \left(\log(n)^{2}\right)$ ( $T_{\infty }^{\text{merge}}(n)=\Theta \left(\log(n)^{2}\right)$ $T_{\infty }^{\text{merge}}(n)=\Theta \left(\log(n)^{2}\right)$ $T_{\infty }^{\text{merge}}(n)=\Theta \left(\log(n)^{2}\right)$ ) $T_{\infty }^{\text{merge}}(n)=\Theta \left(\log(n)^{2}\right)$ ) ${\$ 이다. $\theta \left(\log(n)^{2}\right$ 즉, 프로세서가 한없이 많은 이상적인 시스템에서 그만큼 많은 시간이 소요됨을 의미한다.^[7]^{: 801–802}

참고: $A$ 와 $B$ 를 분할하여 동일한 품목을 $분리$ 하면 C에서 인터리빙이 되며, $A$ 와 B를 교환하면 두 입력 배열 사이에 동일한 품목이 분산될 경우 순서가 파괴된다. 그 결과, 정렬에 사용될 때, 이 알고리즘은 안정적이지 않은 정렬을 생성한다.

언어 지원

일부 컴퓨터 언어는 정렬된 컬렉션을 병합하기 위한 내장형 또는 라이브러리 지원을 제공한다.

C++

C++의 표준 템플릿 라이브러리에는 두 개의 정렬된 반복기 범위를 병합하는 std::merge 기능과 두 개의 연속 정렬된 범위를 인플레이스_merge로 병합하는 std::inplace_merge 기능이 있다. 또한 std::list(연계된 목록) 클래스는 다른 목록을 자체로 병합하는 고유한 병합 방법을 가지고 있다. 병합된 원소의 유형은 (<) 미만 연산자를 지원하거나 사용자 정의 대조군과 함께 제공되어야 한다.

C++17은 순차적, 병렬적, 병렬적, 순차적이지 않은 다른 실행 정책을 허용한다.^[9]

파이톤

파이썬의 표준 라이브러리(2.6년 이후)도 힙큐 모듈에 병합 기능을 가지고 있는데, 이 기능은 여러 개의 정렬된 반복장치를 취해서 하나의 반복기로 병합한다.^[10]

참고 항목

참조

^ ^a ^b Skiena, Steven (2010). The Algorithm Design Manual (2nd ed.). Springer Science+Business Media. p. 123. ISBN 978-1-849-96720-4.
^ ^a ^b ^c Kurt Mehlhorn; Peter Sanders (2008). Algorithms and Data Structures: The Basic Toolbox. Springer. ISBN 978-3-540-77978-0.
^ Katajainen, Jyrki; Pasanen, Tomi; Teuhola, Jukka (1996). "Practical in-place mergesort". Nordic J. Computing. 3 (1): 27–40. CiteSeerX 10.1.1.22.8523.
^ Kim, Pok-Son; Kutzner, Arne (2004). Stable Minimum Storage Merging by Symmetric Comparisons. European Symp. Algorithms. Lecture Notes in Computer Science. Vol. 3221. pp. 714–723. CiteSeerX 10.1.1.102.4612. doi:10.1007/978-3-540-30140-0_63. ISBN 978-3-540-23025-0.
^ Chandramouli, Badrish; Goldstein, Jonathan (2014). Patience is a Virtue: Revisiting Merge and Sort on Modern Processors. SIGMOD/PODS.
^ ^a ^b ^c ^d Greene, William A. (1993). k-way Merging and k-ary Sorts (PDF). Proc. 31-st Annual ACM Southeast Conf. pp. 127–135.
^ ^a ^b Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03384-4.
^ Victor J. Duvanenko (2011), "Parallel Merge", Dr. Dobb's Journal
^ "std:merge". cppreference.com. 2018-01-08. Retrieved 2018-04-28.
^ "heapq — Heap queue algorithm — Python 3.10.1 documentation".

추가 읽기

도널드 크누스 컴퓨터 프로그래밍의 기술 제3권: 정렬과 검색, 제3판 애디슨 웨슬리, 1997년 ISBN 0-201-89685-0. 섹션 5.2.4의 페이지 158–160: 병합에 의한 정렬. 섹션 5.3.2: 최소 비교 병합, 페이지 197–207.

외부 링크

GitHub와 C++ Git에서 소스를 사용한 C#에서의 병렬 및 직렬 병합 고성능 구현허브

[skiena-1] Skiena, Steven (2010). The Algorithm Design Manual (2nd ed.). Springer Science+Business Media. p. 123. ISBN 978-1-849-96720-4.

[toolbox-2] Kurt Mehlhorn; Peter Sanders (2008). Algorithms and Data Structures: The Basic Toolbox. Springer. ISBN 978-3-540-77978-0.

[3] Katajainen, Jyrki; Pasanen, Tomi; Teuhola, Jukka (1996). "Practical in-place mergesort". Nordic J. Computing. 3 (1): 27–40. CiteSeerX 10.1.1.22.8523.

[4] Kim, Pok-Son; Kutzner, Arne (2004). Stable Minimum Storage Merging by Symmetric Comparisons. European Symp. Algorithms. Lecture Notes in Computer Science. Vol. 3221. pp. 714–723. CiteSeerX 10.1.1.102.4612. doi:10.1007/978-3-540-30140-0_63. ISBN 978-3-540-23025-0.

[Chandramouli-5] Chandramouli, Badrish; Goldstein, Jonathan (2014). Patience is a Virtue: Revisiting Merge and Sort on Modern Processors. SIGMOD/PODS.

[greene-6] Greene, William A. (1993). k-way Merging and k-ary Sorts (PDF). Proc. 31-st Annual ACM Southeast Conf. pp. 127–135.

[clrs-7] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03384-4.

[vjd-8] Victor J. Duvanenko (2011), "Parallel Merge", Dr. Dobb's Journal

[9] "std:merge". cppreference.com. 2018-01-08. Retrieved 2018-04-28.

[10] "heapq — Heap queue algorithm — Python 3.10.1 documentation".

[1]

[2]

[3]

[4]

[6]

[7]

[9]

[10]

v t 정렬 알고리즘
이론	계산 복잡성 이론 빅 O 표기법 총순번 목록 배치 안정성 비교 정렬 적응 정렬 정렬 네트워크 정수 정렬 X + Y 정렬 트랜스디코토머스 모형 양자 분류
Exchange sort	버블 정렬 칵테일 셰이커 분류 홀수-짝수 정렬 콤 정렬 Gnome sort 비율 확장 정렬 퀵소트 슬로우토트 스투지 분류 보고소트
선택 정렬	선택 정렬 힙스포트 스무스소트 데카르트 트리 정렬 토너먼트 정렬 사이클 정렬 약한 heap 분류
삽입 정렬	삽입 정렬 조개류 스플레이소트 트리 정렬 라이브러리 정렬 인내 정렬
정렬 병합	병합 정렬 계단식 병합 정렬 병합 정렬 진동 다상 병합 정렬
분포 정렬	미국 국기 종류 비드 정렬 버킷 정렬 버스토트 카운팅 정렬 보간 정렬 비둘기홀 정렬 프록시맵 정렬 라딕스 분류 플래시소트
동시 정렬	비토닉 정렬기 배처 홀수-짝수 병합 쌍방향 정렬 네트워크 샘플포트
잡종류	병합 정렬 차단 커크패트릭-레이시 분류 팀소트 인트로소트 스프레스포트 병합 삽입 정렬
기타	위상 분류 위상전순서 팬케이크 분류 스파게티 종류

Search