광전달함수

카메라, 현미경, 사람의 눈, 프로젝터 등의 광학 시스템의 광학 전송 기능(OTF)은 시스템에서 서로 다른 공간 주파수를 처리하는 방식을 명시한다. 광학 엔지니어는 광학자가 물체나 장면에서 빛을 사진 필름, 검출기 배열, 망막, 스크린 또는 광학 전송 체인의 다음 항목으로 투사하는 방법을 설명하기 위해 사용한다. 변종인 변조 전달 함수(MTF)는 위상 효과를 무시하지만 많은 상황에서 OTF와 동등하다.

어느 하나의 전송 함수는 렌즈 시스템을 통과하는 주기적인 사인파 패턴에 대한 응답을 공간 주파수 또는 주기 및 방향의 함수로 명시한다. 형식적으로 OTF는 포인트 스프레드 함수의 푸리에 변환(PSF, 즉 광학 임펄스 반응, 포인트 소스의 이미지)으로 정의된다. 푸리에 변환의 경우 OTF는 복잡하게 평가되지만, PSF의 중심에서 대칭되는 일반적인 경우에서 실제 평가될 것이다. MTF는 공식적으로 복합 OTF의 크기(절대값)로 정의된다.

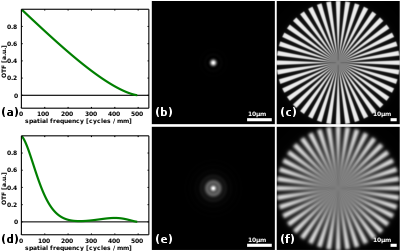
오른쪽의 이미지는 패널 (a)와 (d)의 서로 다른 두 광학 시스템에 대한 광학 전송 기능을 보여준다. 전자는 동공이 원형인 이상적인 회절제한 영상 시스템에 해당한다. 전달 함수는 공간 주파수에 따라 거의 점진적으로 감소하며, 이 경우 밀리미터 당 500 사이클 또는 2μm의 주기로 회절 한계치에 도달할 때까지 감소한다. 이 기간만큼 작은 주기적인 특징이 이 영상 시스템에 포착되기 때문에 해상도는 2μm라고 할 수 있다.^[1] 패널(d)은 초점이 맞지 않는 광학 시스템을 보여준다. 이는 회절제한 영상시스템에 비해 대조가 급격히 감소하는 결과를 초래한다. 대조가 250 사이클/mm 전후, 또는 4μm임을 알 수 있다. 이것은 왜 초점이 맞지 않는 시스템(e,f)의 이미지가 회절제한 시스템(b,c)의 이미지보다 더 흐리게 나타나는지를 설명한다. 초점이 맞지 않는 시스템은 250 사이클/mm 전후의 공간 주파수에서 매우 낮은 대비를 갖지만, 500 사이클/mm의 회절 한계 부근의 공간 주파수에서의 대조는 회절 제한적이라는 점에 유의한다. 패널(f)의 이미지를 면밀히 관찰하면 스포크 대상의 중심 부근에 있는 큰 스포크 밀도에 대해 스포크 구조가 비교적 선명하다는 것을 알 수 있다.

정의 및 관련 개념

광전달함수^[2](OTF)는 포인트스프레드함수(PSF)의 푸리에 변환으로 정의되기 때문에 일반적으로 공간 주파수의 복합값 함수를 말하고 있다. 특정 주기적 패턴의 투영은 각각 투영된 투영의 상대적 대비와 번역에 비례하는 절대값과 복잡한 인수를 가진 복합수로 표현된다.

치수	공간함수	푸리에 변환
1D	라인스프레드 함수 (가장자리-모서리 함수 포함)	2D 광전달 기능의 1D 섹션
2D	점-스프레드 함수	(2D) 광전달 기능
3D	3D 점-스프레드 함수	3D 광전달 기능

종종 대비 감소가 가장 흥미로우며 패턴의 번역을 무시할 수 있다. 상대 대비는 일반적으로 변조 전달 함수(MTF)라고 하는 함수인 광전달 함수의 절대값으로 주어진다. 그것의 값은 얼마나 많은 물체의 대비가 공간 주파수의 함수로 영상에 포착되는지 나타낸다. MTF는 공간 주파수가 1에서 0으로 증가하면 감소하는 경향이 있지만(회절 한계에서) 기능은 단조적이지 않은 경우가 많다. 한편, 패턴 번역도 중요할 때, 광전달함수의 복잡한 주장을 제2의 실제값 함수로, 흔히 위상전달함수(PhTF)라고 하는 것으로 나타낼 수 있다. 복합값 광전달 함수는 다음과 같은 두 가지 실제값 함수의 조합으로 볼 수 있다.

${\displaystyle \mathrm {OTF}(\nu )=\mathrm {MTF}(\nu )e^{i\,\mathrm {PhTF}(\nu )})}$

어디에

${\displaystyle \mathrm {MTF}(\nu )=\left\vert \mathrm {OTF}(\nu )\right\vert ,}$

${\displaystyle \mathrm {PhTF}(\nu )=\mathrm {arg}(\mathrm {OTF}(\nu )),}$

${\displaystyle \mathrm{그리고}}$ $r{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{g}}$ (${\displaystyle \cdot }$ ) ${\displaystyle \mathrm {arg}$(\$cdot )}$은 복잡한 인수 함수를 나타내며$$, $\nu {\displaystyle }$ ${\displaystyle \nu}$은 주기적 패턴의 공간 주파수다. 일반적으로 $\nu {\displaystyle }$ ${\displaystyle \nu}$은 각 차원에 대한 공간 주파수를 가진 벡터로서, 즉 주기적$$ 패턴의 방향도 나타낸다.

잘 초점화된 광학계의 임펄스 응답은 초점면에서 최대치를 갖는 3차원 강도 분포로, 따라서 검출기를 축방향으로 치환하면서 영상 스택을 기록함으로써 측정할 수 있었다. 그 결과, 3차원 광전달 기능은 임펄스 반응의 3차원 푸리에 변환으로 정의할 수 있다. 일반적으로는 1차원 또는 2차원 단면만을 사용하지만, 3차원 광전달 기능은 구조화된 조명현미경과 같은 현미경의 이해를 향상시킬 수 있다.

전송 함수의 ${\displaystyle \mathrm{정의}}$에 따라 O $T{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{F}}$( ${\displaystyle 0}$)${\displaystyle }$= ${\displaystyle M\mathrm{}}$ ${\displaystyle \mathrm{T}}$ F${\displaystyle }$( 0${\displaystyle }$) ${\displaystyle \mathrmat {OTF} (0)=\mathrmat {MTF} (0)}$은 점 소스 개체에서 검출된 빛의 분율을 표시해야 한다$$. 그러나 일반적으로 탐지된 총 빛의 양에 대한 대비가 가장 중요하다. 따라서 검출된 강도로 광전달 기능을 정상화하는 것이 일반적이며, 따라서 $M{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{T}}$ F${\displaystyle }$( ${\displaystyle 0}$) ${\displaystyle \equiv }$ ${\displaystyle 1}$ ${\displaystyle \mathrm {MTF} (0)\equiv$ 1$\}$ .

일반적으로 광전달 기능은 방출된 빛의 스펙트럼과 양극화, 점원 위치 등의 요인에 따라 달라진다. 예를 들어 영상 대비 및 분해능은 일반적으로 영상 중심에서 최적이며 시야의 가장자리로 악화된다. 현저한 변동이 발생한 경우 대표적인 위치나 색상의 집합에 대해 광전달 기능을 계산할 수 있다.

때로는 이진 흑백 스트라이프 패턴을 기반으로 전송 기능을 정의하는 것이 더 실용적이다. 등폭 흑백 주기 패턴에 대한 전송 함수를 대조 전달 함수(CTF)라고 한다.^[3]

예

이상적인 렌즈 시스템의 OTF

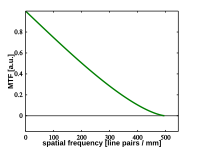
완벽한 렌즈 시스템은 주기적인 패턴을 이동하지 않고 고대비 투영을 제공할 것이므로 광전달 기능은 변조 전달 기능과 동일하다. 일반적으로 대조는 광학 분해능에 의해 정의된 지점에서 0으로 점차 감소한다. 예를 들어, 500 nm의 가시 파장에서 사용되는 완벽하고 감산되지 않은 f/4 광학 영상 시스템은 오른손 그림에서 광학 전송 기능을 나타낼 것이다.

밀리미터 당 500 사이클의 공간 주파수에서 대조가 점차 감소하여 0에 도달한다는 것을 그림에서 알 수 있는데, 즉 영상 투영의 광학적 분해능은 밀리미터 1/500^th, 즉 2마이크로미터라는 것이다. 이에 상응하여, 이 특정한 영상 장치의 경우, 스포크는 회색, 미해결 디스크로 합쳐질 때까지 중앙을 향해 점점 흐려진다. 광전송 기능은 때로는 물체나 표본 공간, 관측 각도, 필름 폭의 단위로 제공되거나 이론적 최대치로 정규화되기도 한다. 둘 사이의 전환은 전형적으로 곱셈이나 나눗셈의 문제다. 예를 들어, 현미경은 일반적으로 모든 것을 10배에서 100배까지 확대하며 반사 카메라는 일반적으로 5미터 거리의 물체를 100배에서 200배의 비율로 격하한다.

디지털 영상 기기의 분해능은 광학뿐만 아니라 픽셀 수, 특히 분리 거리에 의해 제한된다. 나이키스트-샤논 샘플링 정리에 의해 설명되었듯이, 주어진 예시의 광학적 분해능에 일치시키기 위해, 각 컬러 채널의 픽셀은 밀리미터 당 500 사이클의 절반인 1마이크로미터로 분리되어야 한다. 동일한 센서 크기에서 픽셀 수가 많으면 더 미세한 디테일의 해상도가 허용되지 않는다. 반면에 화소 간격이 1마이크로미터보다 크면 화소 간 분리에 의해 분해능이 제한된다. 더욱이 앨리어싱은 화소 충실도를 더욱 떨어뜨릴 수 있다.

불완전한 렌즈 시스템의 OTF

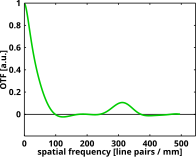
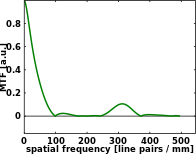
불완전하고 일탈된 영상 시스템은 다음 그림에 표시된 광학 전송 기능을 가질 수 있다.

이상적인 렌즈 시스템으로서, 밀리미터 당 500 사이클의 공간 주파수에서 대조는 0에 도달한다. 그러나 낮은 공간 주파수에서 대비는 앞의 예에서 완벽한 시스템의 대비보다 상당히 낮다. 실제로 밀리미터 당 500 사이클 미만의 공간 주파수에서도 여러 번 대조가 0이 된다. 이는 위의 그림에 표시된 스포크 이미지에서 회색 원형 밴드를 설명한다. 회색 띠 사이에서는 스포크가 흑색에서 백색으로 반전되는 것으로 보이며, 반대로 이를 대조 반전이라고 하며, 광전송 기능의 실제 부분에서 기호 반전과 직접 관련되며, 일부 주기적 패턴에 대한 반주기 변화로 그 자체를 나타낸다.

이상과 불완전한 계통의 분해능이 모두 2μm, 즉 500 LP/mm라고 주장할 수 있지만, 후자의 예시의 영상이 덜 날카롭다는 것은 분명하다. 인식된 품질에 더 부합하는 분해능의 정의는 대신 첫 번째 0, 10μm 또는 100 LP/mm가 발생하는 공간 주파수를 사용한다. 해상도의 정의는 심지어 완벽한 영상 시스템에도 매우 다양하다. 광전달 기능에 의해 보다 완전하고 모호하지 않은 그림이 제공된다.

비회전 대칭 편차를 갖는 광학 시스템의 OTF

광학 시스템, 특히 광학 이상은 항상 회전 대칭인 것은 아니다. 따라서 방향이 다른 주기적 패턴은 주기가 같더라도 다른 대비를 통해 이미징할 수 있다. 따라서 광전달 기능이나 변조 전달 기능은 일반적으로 2차원 기능이다. 다음 그림은 비회전 대칭 이상인 삼포일 광학 시스템에 대해 앞에서 설명한 이상과 불완전한 시스템의 2차원 등가치를 보여준다.

광전송 기능이 항상 실제 가치가 있는 것은 아니다. 기간 패턴은 시스템의 일탈에 따라 임의의 양으로 이동할 수 있다. 이는 일반적으로 비회전-대칭 이상에 해당된다. 위의 그림에서 표면도의 색상은 위상을 나타낸다. 회전 대칭 이상에 대해서는 위상이 0 또는 π 중 하나이고 따라서 전달 함수가 실제 평가되는 반면, 비회전 대칭 이상에 대해서는 전달 함수가 가상 구성요소를 가지며 위상이 지속적으로 변화한다는 것을 알 수 있다.

실제 사례 – 고화질 비디오 시스템

광학 해상도는 카메라 시스템을 기준으로 일반적으로 사용되는 것과 같이 영상의 픽셀 수, 따라서 미세한 디테일을 보여줄 수 있는 가능성만을 설명하지만, 전송 함수는 공간 주파수가 다양한 패턴에 반응하여 주변 픽셀이 흑백에서 백색으로 변하는 능력을 기술하고, 따라서 실제의 능력을 설명한다. 대비를 완전하게 하든 줄여서든 미세한 디테일을 보여주기 위해. 높은 공간 주파수에서 '롤 오프(roll off)'하는 광전달 기능으로 재현한 영상이 일상 언어로 '블러드(blurred)'로 나타난다.

1920 X 1080 픽셀의 현재의 고화질(HD) 비디오 시스템의 예를 들어, 나이키스트 정리는 완벽한 시스템에서 완전한 해결(진정한 흑백 전환으로)이 가능해야 한다고 명시하고 있으며, 달리 1920/2=960 line p의 공간 주파수로 언급된다.사진 너비 또는 사진 너비당 960 사이클(단위 각도당 또는 mm당 주기 측면에서 볼 때 또한 가능하지만 일반적으로 카메라를 다룰 때는 더 명확하지 않고 망원경 등에 더 적절함)에 따라 방송된다. 실제로 이는 사례와는 거리가 멀며, 나이키스트 속도에 접근하는 공간 주파수는 일반적으로 진폭 감소와 함께 재현되므로, 미세한 디테일은 볼 수 있지만 대조적으로 크게 감소한다. 이를 통해 예를 들어, 나중에 설명한 것처럼 오버샘플링을 사용하는 필름 스캐너에서 파생된 표준 화질 텔레비전 사진이 변조 전달 기능이 떨어지는 카메라에서 촬영한 고화질 사진보다 더 선명하게 보일 수 있다는 흥미로운 관찰이 나오게 된다. 이 두 그림은 종종 놓치는 흥미로운 차이를 보여주는데, 전자는 특정 지점까지의 세부 사항에 대해 완전한 대조를 이루지만, 후자는 더 미세한 세부사항을 포함하지만, 전반적으로 열악하게 보일 정도로 대비를 줄인 것이다.

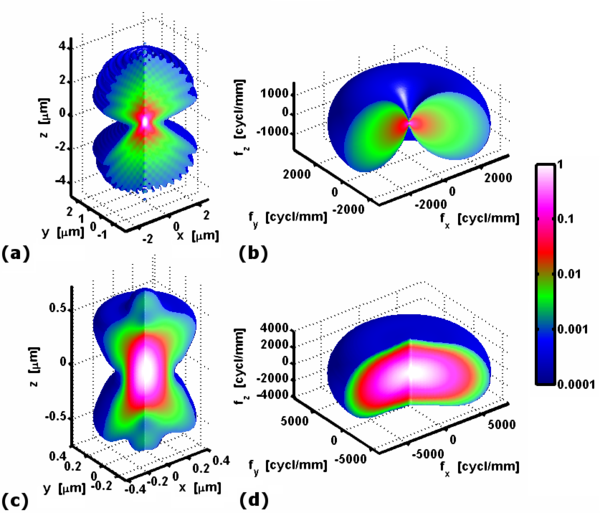
3차원 광전달 기능

일반적으로 영상을 평면 또는 2차원이라고 생각하지만 영상 시스템은 영상 공간에 3차원 강도 분포를 생성하여 원칙적으로 측정할 수 있다. 예를 들어 2차원 센서를 변환하여 3차원 강도 분포를 캡처할 수 있다. 포인트 소스의 이미지 또한 3D 포인트 스프레드 함수로 표현될 수 있는 3차원(3D) 강도 분포다. 예를 들어 오른쪽 그림은 콘포칼로컬 현미경(c)과 함께 광야 현미경(a)의 물체 공간에서 3D 점-스프레드 기능을 보여준다. 숫자 간극이 1.49인 동일한 현미경 목표를 사용하지만, concocal point 스프레드 기능은 측면 치수(x,y)와 축 치수(z) 모두에서 더 콤팩트한 것이 분명하다. 3차원 모두에서 콘코칼로컬 현미경의 해상도가 광야 현미경의 해상도보다 우수하다는 결론은 옳을 수 있다.

3차원 광전달 기능은 3D 포인트 스프레드 함수의 3차원 푸리에 변환으로 계산할 수 있다. 색상으로 구분된 크기는 패널 (b)와 (d)에 각각 표시되며, 패널 (a)와 (c)에 표시된 포인트 스프레드 기능에 해당한다. 광장 현미경의 전달 기능은 3차원 모두에서 콘코칼로컬 현미경의 절반에 해당하는 지지대를 가지고 있어 이전에 지적한 광장 현미경의 낮은 해상도를 확인시켜 준다. z축을 따라 x = y = 0의 경우 전송 함수는 원점을 제외한 모든 위치에서 0이 된다는 점에 유의하십시오. 이 사라진 원뿔은 광학 단면현미경을 이용한 광학 단면을 방지하는 것으로 잘 알려진 문제다.^[4]

초점 평면의 2차원 광전달 기능은 z축을 따라 3D 광전달 기능을 통합해 계산할 수 있다. 와이드 필드 현미경 (b)의 3D 전송 기능이 z축에서 z ≠ 0에 0이기는 하지만, 그 일체형인 2D 광전송은 x = y = 0에서 최대치에 도달한다. 이는 3D 광전달 기능이 원점 x = y = z = 0에서 분산되기 때문에 가능한 것이다. 3D 광전달함수의 z축에 따른 함수 값은 디락 델타 함수에 해당한다.

계산

대부분의 광학 설계 소프트웨어는 렌즈 설계의 광학 또는 변조 전달 기능을 계산하는 기능을 가지고 있다. 여기 예에서와 같은 이상적인 시스템은 Julia, GNU 옥타브 또는 Matlab과 같은 소프트웨어를 사용하여 쉽게 숫자로 계산되며, 어떤 특정한 경우에는 분석적으로 계산하기도 한다. 광전달 기능은 다음 두 가지 접근법에 따라 계산할 수 있다.^[5]

1. 일관성 없는 점 스프레드 함수의 푸리에 변환으로, 또는
2. 광학계통의 동공기능의 자동추적으로서.

수학적으로 두 가지 접근방식은 동일하다. 숫자 계산은 일반적으로 푸리에 변환을 통해 가장 효율적으로 수행되지만, 분석적 계산은 자동 상관 접근방식을 사용하여 더 추적가능할 수 있다.

예

원형 개구부가 있는 이상적인 렌즈 시스템

동공 기능의 자동 상관

광전송 기능은 포인트 스프레드 기능의 푸리에 변환이고, 포인트 스프레드 기능은 역 푸리에 변환 동공 기능의 사각 절대값이기 때문에 동공 기능에서 직접 광전송 기능도 계산할 수 있다. 콘볼루션 정리로부터 광전달 기능이 사실상 동공 기능의 자기 상관임을 알 수 있다.^[5]

원형 개구부를 가진 이상적인 광학 시스템의 동공 기능은 단위 반지름의 디스크다. 따라서 이러한 시스템의 광전송 기능은 ${\displaystyle 2}$ ${[\displaystyle 2\nu }$의 거리에서 두 개의 동일한 디스크 사이의 교차 영역에서 기하학적으로 계산할 수 있으며$,$ 여기서 $\nu {\displaystyle }$ ${\displaystyle \nu}$은 가장 높은 전송 주파수로 정규화된 공간 주파수다.^[2] 일반적으로 광전달 기능은 $\nu {\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle \nu =0$에 대해 최대값 1로 정규화되므로 결과 영역은 $area{\displaystyle }$ ${\displaystyle \pi }$로 나누어야 한다$.$

교차 영역은 두 개의 동일한 원형 세그먼트의 면적 합으로 ${\displaystyle 계산}$할 수 있다$:$ $\theta {\displaystyle }$/ ${\displaystyle 2\mathrm{}}$ -${\displaystyle \sin }$ ${\displaystyle (\theta }$ )${\displaystyle }$/ 2 ${\displaystyle \theta /2-\sin(\theta )/2}$ 여기서 $where{\displaystyle }$ ${\displaystyle \theta }$은 원 세그먼트 각도. By substituting ${\displaystyle \nu =\cos(\theta /2)}$, and using the equalities ${\displaystyle \sin(\theta )/2=\sin(\theta /2)\cos(\theta /2)}$ and ${\displaystyle 1=\nu ^{2}+\sin(\arccos($$\nu )^{2$ 면적 방정식은 ${\displaystyle \arccos }$ ${\displaystyle }$ (${\displaystyle \nu }$ ) -${\displaystyle \nu \sqrt{\mathrm{}}}$ 1 -${\displaystyle \sqrt{{}^{}}}$ ${\displaystyle \sqrt{{2\mathrm{}}^{}}}$ ${\$ 따라서 표준화된 광전달 기능은 다음과 같이 제공된다.

${\displaystyle \operatorname {OTF}(\nu )={\frac {2}{\pi }}\왼쪽(\arccos(\nu )- \nu {1-\nu ^{2}}\오른쪽).}$

좀 더 자세한 논의는 및 에서 찾을 수 있다.^{[2]: 152–153}

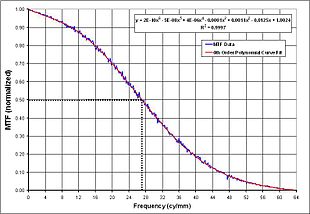
수치평가

1차원 광전달 함수는 라인 확산 함수의 이산 푸리에 변환으로 계산할 수 있다. 이 데이터는 공간 주파수 데이터를 기준으로 그래프로 표시된다. 이 경우 MTF 대 공간 주파수 곡선에 6차 다항식이 적합되어 추세를 나타낸다. 50% 컷오프 주파수는 해당 공간 주파수를 산출하도록 결정된다. 따라서 시험 대상 장치의 최량 초점의 대략적인 위치는 이 데이터로부터 결정된다.

라인 확산 함수(LSF)의 푸리에 변환은 다음 방정식으로 분석할 수 없다.

${\displaystyle \operatorname {MTF} ={\mathcal {F}\왼쪽[\operatorname {LSF}\right]\qquad \qquad \qquad \qquad \operatorname {MTF} =\int f(x)e^{-i2\pi \,xs}\,dx}\,dx}$

따라서 푸리에 변환은 이산 푸리에 변환 $D{\displaystyle \mathcal{}}$ ${\displaystyle \mathcal{F}}$ ${\displaystyle \mathcal{T}}$ ${\$을(를) 사용하여 숫자로 근사치를 구한다$.$^[6]

${\displaystyle \operatorname {MTF} ={\mathcal {DFT}}[\operatorname {LSF} ]=Y_{k}=\sum _{n=0}^{N-1}y_{n}e^{-ik{\frac {2\pi }{N}}n}\qquad k\in [0,N-1]}$

어디에

• ${\displaystyle Y_{}}$ ${\displaystyle k_{}}$ $displaystyle Y_{k}\,}$ $$= MTF의 $k$ ${\displaystyle {\text{th}}^{}}$ ${\$ k$^{\text{th}}$ 값
• ${\displaystyle N}$ ${\$ N$\,}$ $$= 데이터 점 수
• ${\displaystyle n}$ $[\$ n$\,}$ $$= 색인
• ${\displaystyle k}$ ${\$ $$= k ${\displaystyle {\text{th}}^{}}$ ${\$ k$^{\text}}$ LSF 데이터의 기간$$
• ${\displaystyle y_{}}$ ${\displaystyle n_{}}$ $displaystyle y_{n}\,}$ $$= ${\displaystyle {\text{n}}^{}}$ $displaystyle n^{\text}\,}$픽셀$$ 위치
• ${\displaystyle i={\sqrt{-1}$

${\displaystyle e^{\pm ia}=\cos(a)\,\pm \,i\sin(a)}$

${\displaystyle \operatorname {MTF} ={\mathcal {DFT}}[\operatorname {LSF} ]=Y_{k}=\sum _{n=0}^{N-1}y_{n}\left[\cos \left(k{\frac {2\pi }{N}}n\right)-i\sin \left(k{\frac {2\pi }{N}}n\right)\right]\qquad k\in [0,N-1]}$

그런 다음 MTF는 공간 주파수를 기준으로 표시되며, 이 테스트와 관련된 모든 관련 데이터는 해당 그래프에서 확인할 수 있다.

벡터 전송 함수

현미경 검사에서 발견되는 것과 같은 높은 숫자의 구멍에서는 빛을 운반하는 들판의 벡터적 특성을 고려하는 것이 중요하다. 데카르트 축에 해당하는 3개의 독립된 구성 요소에서 파동을 분해함으로써 각 구성 요소에 대해 포인트 스프레드 함수를 계산하여 벡터 포인트 스프레드 함수로 결합할 수 있다. 마찬가지로 ()와 ()^[8]와 ^[7]같이 벡터 광전달 기능을 결정할 수 있다.

측정

광전달 기능은 광학시스템 설계에 유용할 뿐만 아니라 제조된 시스템의 특성화에도 유용하다.

점 스프레드 함수에서 시작

광전달 기능은 광학계 임펄스 반응의 푸리에 변환으로 정의되며, 포인트 스프레드 기능이라고도 한다. 따라서 광전달 기능은 포인트 소스의 이미지를 먼저 획득하고 샘플링된 이미지에 2차원 이산 푸리에 변환을 적용함으로써 쉽게 얻을 수 있다. 예를 들어 이러한 포인트 소스는 핀홀, 형광 또는 금속 마이크로스피어가 있는 화면 뒤에 밝은 빛이 될 수 있고, 단순히 화면에 점으로 그려진 점이 될 수 있다. 포인트 스프레드 기능을 통한 광전달 기능의 계산은 포인트 소스의 다양한 위치 및 파장 스펙트럼에 대한 절차를 반복함으로써 공간적 다양성과 색도 일탈로 광학을 완전 특성화할 수 있어 다재다능하다.

공간 불변 광학 장치에 확장 테스트 객체 사용

이상이 공간적으로 불변한다고 가정할 수 있는 경우, 대체 패턴을 사용하여 선과 가장자리 등의 광전달 기능을 결정할 수 있다. 해당 전송 함수를 각각 라인스프레드 함수와 에지스프레드 함수로 한다. 이렇게 확장된 물체는 영상에서 더 많은 픽셀을 비추고 신호 대 잡음 비율이 더 크기 때문에 측정 정확도를 향상시킬 수 있다. 광전송 기능은 이 경우에 이미지의 2차원 이산 푸리에 변환으로 계산되며 확장된 물체의 변환으로 나눈다. 일반적으로 선 또는 흑백 가장자리가 사용된다.

라인스프레드 함수

원점을 통과하는 선의 2차원 푸리에 변환은 원점과 직교하는 선이다. 따라서 디비저는 단일 치수를 제외한 모든 치수에 대해 0이며, 결과적으로 광전달 기능은 단일 선간격 함수(LSF)를 사용하여 단일 치수에 대해서만 결정할 수 있다. 필요한 경우 다양한 각도에서 선으로 측정을 반복해 2차원 광전달 기능을 파악할 수 있다.

라인 스프레드 기능은 두 가지 다른 방법을 사용하여 찾을 수 있다. 이 값은 슬릿 테스트 대상이 제공하는 이상적인 라인 근사치에서 직접 찾을 수 있거나 다음 하위 섹션에서 설명하는 가장자리 확산 함수에서 도출할 수 있다.

에지-스프레드 함수

가장자리의 2차원 푸리에 변환 역시 가장자리와 직교하는 단일 선에서 0이 아닌 것에 불과하다. 이 기능을 에지 스프레드 함수(ESF)라고도 한다.^[9][10] 그러나 이 선의 값은 원점으로부터의 거리에 반비례한다. 이 기법으로 얻은 측정 영상이 카메라의 넓은 영역을 비추지만, 이는 주로 낮은 공간 주파수에서의 정확도에 도움이 된다. 라인 확산 기능과 마찬가지로 각 측정은 광전달 기능의 단일 축만 결정하므로 광학 시스템이 회전 대칭이라고 가정할 수 없는 경우 반복적인 측정이 필요하다.

오른쪽 그림에서 볼 수 있듯이, 운영자는 검은 몸체에 의해 역광 처리된 칼날 테스트 대상 이미지의 가장자리를 둘러싸는 상자 영역을 정의한다. 박스 면적은 총 프레임 면적의 ^{[citation needed]}약 10%로 정의된다. 영상 픽셀 데이터는 2차원 배열(픽셀 강도 및 픽셀 위치)로 변환된다. 어레이 내 각 라인의 진폭(픽셀 강도)이 정규화 및 평균화된다. 이것은 에지 스프레드 기능을 산출한다.

${\displaystyle \operatorname {ESF} ={\frac {X-\mu }{\sigma }}\qquad \qquad \sigma \,={\sqrt {\frac {\sum _{i=0}^{n-1}(x_{i}-\mu \,)^{2}}{n}}}\qquad \qquad \mu \,={\frac {\sum _{i=0}^{n-1}x_{i}}{n}}}$

어디에

• ESF = 정규화된 픽셀 강도 데이터의 출력 배열
• ${\displaystyle X}$ ${\$ $$= 픽셀 강도 데이터의 입력 배열
• ${\displaystyle x_{}}$ ${\displaystyle i_{}}$ $displaystyle x_{i}\,}$ $$= $X$의 i 요소^th ${\$
• $[\$ $$= 픽셀 강도 데이터의 평균 값
• ${\displaystyle \sigma }$ ${\$ $$= 픽셀 강도 데이터의 표준 편차
• ${\displaystyle n}$ $[\$ $$= 평균적으로 사용된 픽셀 수

라인 스프레드 함수는 에지 스프레드 함수의 첫 번째 파생 모델과 동일하며,^[11] 수치적 방법을 사용하여 구별된다. 에지 스프레드 기능이 보다 실용적일 경우 다음과 같이 라인 스프레드 기능을 결정할 수 있다.

${\displaystyle \operatorname {LSF} ={\frac {d}{dx}\operatorname {ESF}(x)}$

일반적으로 ESF는 이산형 지점에서만 알려져 있으므로 LSF는 유한 차이를 사용하여 수치적으로 근사치를 나타낸다.

${\displaystyle \operatorname {LSF} ={\frac {d}{dx}\operatorname {ESF}(x)\약 {\fract {\Delta \operatorname {ESF}{\Delta x}}}}}}}$

${\displaystyle \operatorname {LSF} \ 약 {\frac {\operatorname {ESF} _{i+1}-\operatorname {ESF} _{i-1}{2}{2}(x_{i+1}-x_{i}) \i}}}}$

여기서:

• ${\displaystyle i}$ ${\$ i$\,}$ $$= 색인 $i{\displaystyle }$= ${\displaystyle 1}$,${\displaystyle 2}$,${\displaystyle \dots ,}$ ${\displaystyle n}$- ${\displaystyle 1}$ ${\displaystyle i=1,2,\reason,n-1}$
• ${\displaystyle {}_{}}$$x{\displaystyle {}^{}}$ ${\displaystyle i_{}}$ $displaystyle$ $x_{i}\,}$ $$= ${\displaystyle {\text{i}}^{}}$ $displaystyle$ $i^{\text{th}\,}$ 위치$$
• ${\displaystyle {\mathrm{ESF}}_{}}$ ${\displaystyle i_{}}$ $displaystyle \operatorname {ESF} _{i}\,}$ $$= i ${\displaystyle {\text{th}}^{}}$ $displaystyle$ i$^{\text}\,}$픽셀의$$ ESF

검은색 및 흰색 선 그리드 사용

흔히 '샤프니스'는 흑백 교대선의 격자무늬를 기준으로 판단되지만 흑백(일반 패턴의 흐릿한 버전)에 이르는 사인파 편차를 사용하여 엄격하게 측정해야 한다. 사각파 패턴을 사용하는 경우(단순 흑백선)에는 앨리어싱의 위험이 더 클 뿐만 아니라 사각파의 기본 성분이 사각파 자체의 진폭보다 높다는 사실을 고려해야 한다(조화성 성분이 피크 진폭을 감소시킨다). 따라서 사각파 시험 차트는 낙관적인 결과(실제 달성보다 높은 공간 주파수의 분해능)를 보여줄 것이다. 사각파 결과를 '대비 전달 함수'(CTF)라고 부르기도 한다.

일반 카메라 시스템의 MTF에 영향을 미치는 요인

실제로 많은 요인들은 나이키스트 비율 바로 아래 공간적 주파수를 가진 패턴은 보이지 않을 수도 있고, 흑백 색조가 아닌 회색으로 '깨끗하게' 나타날 수 있는 가장 좋은 패턴과 같이 재현된 이미지를 상당히 흐리게 한다. 주요 요인은 대개 완벽한 '브릭 월' 광학 필터(디지털 카메라와 비디오 캠코더에서 특정 흐릿한 특성을 가진 '상판' 또는 렌즈로 실현되는 경우가 많다. 이러한 필터는 디스플레이의 나이키스트 속도 이상의 공간 주파수를 제거하여 앨리어싱을 줄이는 데 필요하다.

광전달 기능을 유지하기 위한 오버샘플링 및 다운변환

카메라와 같은 디지털 영상 시스템에서 가능한 이론적 선명도에 접근하는 유일한 방법은 최종 영상의 샘플보다 카메라 센서의 픽셀을 더 많이 사용하는 것이며, 유지관리하는 동안 앨리어싱을 피하기 위해 나이키스트 비율 이상의 고주파를 차단하는 특수 디지털 처리를 사용하는 '다운콘버터' 또는 '인터폴레이트'를 사용하는 것이다.ng 해당 주파수까지 합리적으로 평탄한 MTF. 이러한 접근 방식은 1970년대에 처음 비행점 스캐너가 개발되었을 때, 그리고 나중에 CCD 라인 스캐너가 개발되었는데, 이 스캐너는 필요한 것보다 더 많은 픽셀을 샘플링한 다음 다운변환하여, 이것이 비디오 카메라로 촬영한 다른 소재보다 텔레비전에서 영화가 항상 더 선명하게 보이는 이유다. 이론적으로 올바른 보간 또는 하향 변환 방법은 강력한 처리가 필요한 2차원 sin(x)/x 가중 기능을 가진 콘볼루션으로 실현되는 가파른 저역 통과 공간 필터를 사용하는 것이다. 실제로 이것에 대한 다양한 수학적 근사치를 사용하여 처리 요건을 감소시킨다. 이러한 근사치는 현재 영상 편집 시스템과 포토샵과 같은 영상 처리 프로그램에서 광범위하게 구현되고 있다.

고대비 MTF의 표준 화질 비디오가 오버샘플링을 통해서만 가능하듯이, 완전한 이론적 선명도를 갖춘 HD 텔레비전은 해상도가 현저히 높은 카메라부터 시작하여 디지털 필터링이 뒤따라야 가능하다. 현재 영화가 영화관에서 4k, 심지어 8k 비디오로 촬영되고 있기 때문에, 우리는 HDTV에서 더 높은 수준의 영화나 소재 촬영에서만 최고의 사진을 볼 수 있을 것으로 기대할 수 있다. 우리가 카메라에서 사용되는 픽셀의 수를 아무리 늘린다고 해도, 완벽한 광학 공간 필터가 없는 한, 이것은 항상 사실일 것이다. 마찬가지로, 5 메가픽셀 스틸 카메라에서 얻은 5 메가픽셀 이미지는 동일한 품질의 10 메가픽셀 스틸 카메라에서 하향 변환한 후 얻은 5 메가픽셀 이미지보다 더 선명할 수 없다. 고대비 MTF를 유지하는 문제 때문에, BBC와 같은 방송사들은 오랫동안 표준 화질 텔레비전을 유지하는 것을 고려했지만, 훨씬 더 많은 픽셀을 촬영하고 시청함으로써 그것의 질을 향상시키는 것을 고려했다. (앞서 언급했듯이, 그러한 시스템은 인상적이긴 하지만, 궁극적으로 매우 미세한 디테일이 부족하다.)uh 감쇠, 트루 HD 시청의 효과 향상).

디지털 카메라와 캠코더의 또 다른 요소는 렌즈 해상도다. 렌즈는 1920년 수평선을 '해제'한다고 말할 수 있지만, 그렇다고 해서 흑백에서 백색으로 완전한 변조를 하는 것은 아니다. '변조 전달함수'(위상이 무시된 광전달함수의 크기를 지칭하는 용어일 뿐)는 렌즈 성능의 참된 측도를 제공하며, 공간 주파수에 대한 진폭 그래프로 표현된다.

렌즈 구멍 회절도 MTF를 제한한다. 렌즈 간극을 줄이면 대개 이상이 감소하고 따라서 MTF의 평탄도가 개선되지만, 축소된 간극이 이미지 센서 전체로 빛을 확산시키는 회절 때문에 분해능이 감소하는 렌즈와 이미지 센서 크기 이상의 렌즈 및 이미지 센서 크기에 대한 최적의 간극이 있다. 이것은 플레이트 카메라와 심지어 35mm 필름의 시대에는 거의 문제가 되지 않았지만, 일부 디지털 카메라와 특히 비디오 카메라에 사용되는 매우 작은 포맷 센서로 인해 극복할 수 없는 한계가 되었다. 1세대 HD 소비자 캠코더는 1/4인치 센서를 사용했는데, 이 센서의 경우 약 f4보다 작은 구경이 해상도를 제한하기 시작했다. 전문 비디오 카메라조차 대부분 2/3인치 센서를 사용하며 필름 형식에 정상으로 여겨졌을 f16 주변의 조리개 사용을 금지하고 있다. 특정 카메라(예: 펜탁스 K10D)는 "MTF 자동 노출" 모드를 특징으로, 조리개 선택이 최대 선명도에 최적화되어 있다. 일반적으로 이것은 조리개 범위의 중간 어딘가를 의미한다.^[12]

대형 DSLR 추세 및 MTF 잠재력 향상

최근 저조도 감도와 좁은 필드 효과의 필요성에 의해 구동되는 대형 이미지 포맷 디지털 싱글렌즈 반사 카메라의 사용으로 전환되고 있다. 이것은 이러한 카메라들이 심지어 전문 HD 비디오 카메라보다 일부 영화와 텔레비전 프로그램 제작자들에 의해 선호되게 만들었는데, 그들의 '영화적' 잠재력 때문이다. 이론적으로 16메가픽셀과 21메가픽셀 센서가 장착된 카메라의 사용은 앨리어싱을 없애기 위한 디지털 필터링과 함께 카메라 내부의 하향 변환에 의해 거의 완벽한 예리함의 가능성을 제공한다. 그러한 카메라는 매우 인상적인 결과를 낳으며, 디지털 필터링이 앨리어싱으로부터 진정한 자유를 가진 평평한 MTF의 실현에 대한 표준 접근방식이 되면서 대규모 다운 변환을 향한 비디오 제작의 길을 선도하고 있는 것으로 보인다.

광전달 기능의 디지털 반전

광학적 효과로 인해 대조가 차선일 수 있으며 디스플레이의 나이키스트 주파수에 도달하기 전에 0에 근접한다. 광학 대비 감소는 표시 또는 추가 처리 전에 선택적으로 공간 주파수를 디지털로 증폭시켜 부분적으로 역전시킬 수 있다. 보다 진보된 디지털 이미지 복원 절차가 존재하지만, 단순성과 효율성으로 종종 Wiener deconvolution 알고리즘을 사용한다. 이 기법은 이미지의 공간 스펙트럼 성분을 곱하기 때문에 앨리어싱 등으로 인한 노이즈와 오차도 증폭시킨다. 따라서 신호 대 잡음 비율이 충분히 높은 양질의 기록에만 효과적이다.

제한 사항

일반적으로 점 분산 기능, 점원의 영상도 파장(색상), 장 각도(측면 점원 위치) 등의 요인에 따라 달라진다. 그러한 변화가 충분히 점진적인 경우, 광학 시스템은 일련의 광전달 기능으로 특징지어질 수 있다. 그러나 측면 번역 시 포인트 소스의 이미지가 갑자기 바뀌면 광전달 기능은 광학 시스템을 정확하게 기술하지 않는다.

참고 항목

• 보케
• 감마 보정
• 최소 확인 가능한 대비
• 최소 분해 가능 온도 차이
• 광학 분해능
• 신호 대 잡음 비
• 신호전달함수
• 스트렐 비
• 전달함수
• 웨이브프론트 부호딩

참조

외부 링크

• Glenn D의 "변조 전송 기능". SPIE Optipedia의 보어맨.
• Optikos Corporation의 "MTF 및 기타 렌즈의 특성 측정 방법"