다차원 샘플링

디지털 신호 처리에서 다차원 샘플링은 다차원 변수의 함수를 이산형 점 집합에서 측정한 함수의 개별 값 집합으로 변환하는 과정이다.본 기사는 개별 점 격자에서 측정된 수 제한 함수를 완벽하게 재구성할 수 있는 조건에 대한 Petersen과 Middleton으로^[1] 인해 기본적인 결과를 제시한다.피터슨-미들턴 정리라고도 하는 이 결과는 고차원 유클리드 공간에 대한 1차원 대역제한 함수를 샘플링하기 위한 나이키스트-샤논 샘플링 정리의 일반화다.

본질적으로, 피터슨-미들턴 정리는 격자가 충분히 괜찮다면, 무한히 많은 점의 격자 위에 있는 그것의 값들로부터 완벽하게 재구성될 수 있다는 것을 보여준다.그 정리는 완벽한 재구성이 가능한 격자의 조건을 제공한다.

나이키스트-샤논 샘플링 정리와 마찬가지로, 이 정리는 포인트의 무한도에 걸쳐 샘플링되는 기능에만 적용되므로, 어떤 실제 상황의 이상화도 가정한다.완벽한 재구성은 이상화된 모델에 대해 수학적으로 가능하지만 실제 기능과 샘플링 기법에 대한 근사치일 뿐이다. 비록 실제로 매우 좋은 경우가 많지만 말이다.

예선

이 절에는 참조, 관련 판독 또는 외부 링크 목록이 포함되지만, 인라인 인용구가 부족하기 때문에 출처가 불분명하다. 보다 정확한 인용 부호를 도입하여 이 섹션을 개선할 수 있도록 도와주십시오. (2014년 10월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

한 차원에서의 대역제한함수의 개념은 더 높은 차원에서의 와벤넘버 제한함수의 개념으로 일반화될 수 있다.n차원 유클리드 공간에 대한 통합형$$ 함수 $f{\displaystyle }$ (${\displaystyle \cdot }$ )${\displaystyle$ f$(\cdot )}$의 푸리에 변환은 다음과 같이 정의된다는 점을 상기하십시오.

${\displaystyle {\f}(\xi )={\mathcal {F}(f)(\xi )=\int_{\Re ^{n}f(x)e^{-2\pi i\langle x,\xi \},dx}$

여기서 x와 ξ은 n차원 벡터, $⟨{\displaystyle }$ x ,${\displaystyle \xi }$ ⟩ ${\displaystyle ⟩}$ ${\displaystyle \langle x,\xi \angle }$은 벡터의 내부 제품이다.The function ${\displaystyle f(\cdot )}$ is said to be wavenumber-limited to a set ${\displaystyle \Omega }$ if the Fourier transform satisfies ${\displaystyle {\hat {f}}(\xi )=0}$ for ${\displaystyle \xi \notin \Omega }$.

마찬가지로 균일하게 간격을 두고 1차원 시료채취 지점의 구성은 더 높은 치수에서 격자로 일반화할 수 있다.A lattice is a collection of points ${\displaystyle \Lambda \subset \Re ^{n}}$ of the form ${\displaystyle \Lambda =\left\{\sum _{i=1}^{n}a_{i}v_{i}\; \;a_{i}\in \mathbb {Z} \right\}}$ where {v₁, ..., v_n} is a basis for ${\displaystyle \Re ^{n}}$.$\lambda {\displaystyle \mathrm{}}$ ${\displaystyle \Lambda }$에 해당하는$$ 상호 격자 lat ${\displaystyle \Gamma }$은(는) 다음에 의해 정의된다$$.

${\displaystyle \Gamma =\left\{\sum_{i=1}^{n}a_{i}u_{i}\; \; \a_{i}\in \mathb {Z}\right\}}}}}}}}}$

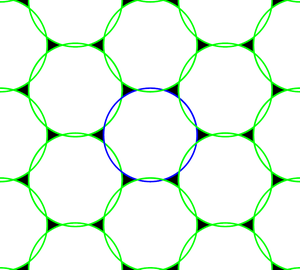
${\displaystyle {}_{}}$서 벡터 ${\displaystyle u_{}}$ ${\displaystyle i_{}}$$displaystyle u_{i}$를 선택하여 satisfy${\displaystyle }$u i , v j${\displaystyle {}_{}}${${\displaystyle }$= ${\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$_${ij}}}}.$That is, if the vectors ${\displaystyle u_{i}}$ form columns of a matrix ${\displaystyle A}$ and ${\displaystyle v_{i}}$ the columns of a matrix ${\displaystyle B}$, then ${\displaystyle A=B^{-T}}$. An example of a sampling lattice in two dimensional space is a hexagonal lattice depic그림 1의 테드.해당 역수 격자는 그림 2와 같다.2차원의 정사각형 격자의 상호 격자는 또 다른 정사각형 격자다.3차원 공간에서 얼굴 중심 입방체(FCC) 격자의 상호 격자는 신체 중심 입방체(BCC) 격자다.

정리

$let{\displaystyle \mathrm{}}$ ${\displaystyle \Lambda}$은(는) ${\displaystyle {\Re n}^{}}$ ${\$ 및 $\gamma {\displaystyle \mathrm{}}$ ${\displaystyle \Gamma}$의 해당$$ 역수 격자를 나타낸다$$.피터슨과 Middleton[1]의 정리에서는 f(⋅){\displaystyle f(\cdot)}⊂ℜ n{\displaystyle \Omega \subset\Re ^{n}}정확히 Λ{\Lambda\displaystyle}에 대한 측정에서 재건축될 수 있는 1세트 Ω에 wavenumber-limited은 기능이 집합 Ω{\displaystyle \Omega}되씩 제공했다.sshift x가 상호 격자$ice$의 0이 아닌 요소인$$$\Omega {\displaystyle \mathrm{}}$+ ${\displaystyle x}$ ${\$$displaystyle \Oomega$$+x}$과(와) 겹치지 않음$.$ $즉{\displaystyle }$, f${\displaystyle }$( ${\displaystyle \cdot }$) ${\displaystyle f(\cdot$)는 제공된$$ $\lambda {\displaystyle \mathrm{}}$ ${\displaystyle \Lambda}$에 대한 측정에서 정확히 재구성할 수 있다$$.${\displaystyle \mathrm{\Omega }}$ ${\displaystyle \cap \{}$ ${\displaystyle x}$+ y${\displaystyle }$: ${\displaystyle y}$ ${\displaystyle \in }$ ${\displaystyle \mathrm{\Omega }\}}$ = ${\displaystyle \mathrm{\varnothing }}${\$displaystyle \Oomega \cap$\{$x+y:y\$$in{\displaystyle }$$$\${\displaystyle \mathrm{Oomega}}$ $\}=\$$ema$${\displaystyle }$\$displaystyle$x$\$in$$ $\ma \setma$\{$0$

재건

는 푸아송 합 공식의 높은 치수[2]에 대한 일반화는 격자 Λ{\Lambda\displaystyle}에 함수 f(⋅){\displaystyle f(\cdot)}의 견본을,{f()):)∈ Λ}{\displaystyle\와 같이{f()):x\in \Lambda)}}, functi을 정기적으로 총체를 창출하기에 충분하기 위해 사용될 수 있다.에${\displaystyle \stackrel{}{f}}$ ${\displaystyle \stackrel{}{^}}$ (${\displaystyle \cdot }$ ) ${\displaystyle {\hat {f}(\cdot )}$.결과는 다음과 같다.

${\displaystyle {\hat {f}}_{s}(\xi )\ {\stackrel {\mathrm {def} }{=}}\sum _{y\in \Gamma }{\hat {f}}\left(\xi -y\right)=\sum _{x\in \Lambda } \Lambda f(x)\ e^{-i2\pi \langle x,\xi \rangle },}$

(Eq.1)

여기서 ${\displaystyle \lambda \mathrm{}}$ $displaystyle \Lambda }$은 벡터 {v₁, ..., v_n}에 의해 형성된 병렬 처리된 볼륨을 나타낸다$$.이 주기 함수는 흔히 샘플링된 스펙트럼이라고 하며, 높은 차원에서 이산 시간 푸리에 변환(DTFT)의 아날로그로 해석할 수 있다.If the original wavenumber-limited spectrum ${\displaystyle {\hat {f}}(\cdot )}$ is supported on the set ${\displaystyle \Omega }$ then the function ${\displaystyle {\hat {f}}_{s}(\cdot )}$ is supported on periodic repetitions of ${\displaystyle \Omega }$ shifted by points on the reciprocal lattice ${\displaystyle \Gamma }$. If the conditions of the Petersen-Middleton theorem are met, then the function ${\displaystyle {\hat {f}}_{s}(\xi )}$ is equal to ${\displaystyle {\hat {f}}(\xi )}$ for all ${\displaystyle \xi \in \Omega }$, and hence the original field표본으로부터 정확히 재구성될 수 있다.이 경우 재구성된 필드는 원래 필드와 일치하며 샘플의 용어로 다음과 같이 표현할 수 있다.

${\displaystyle \underset{}{f}}$( x${\displaystyle }$)${\displaystyle }$= ${\displaystyle \underset{}{}}$ y ${\displaystyle \underset{}{\in }}$ ${\displaystyle \lambda \underset{}{}\mathrm{}}$ ${\displaystyle ˇ{\stackrel{}{}}_{}}$ ω ${\displaystyle {\stackrel{}{\omega }}_{}}$ ω ω ${\displaystyle \omega {}_{}\Omega }$ (${\displaystyle y}$-${\displaystyle }$x )$${\$displaystyle f(x)=\sum _{$y\$in \Lambda }}\Lambda f$(y$){\chi$}}}}{\$cHEmai }}}}}}}}}{-x$ ,

(Eq.2)

여기서 $\chi {\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle {\stackrel{}{ˇ}}_{}}$ ${\displaystyle {\Omega }_{\mathrm{}}}$ ${\displaystyle (\cdot }$ ) ${\displaystyle {\check${\chi $}_{\Oomega }(\cdot$ )은$$ 집합 $\Omega {\displaystyle \mathrm{}}$ ${\displaystyle \Oomega}$의 특성 함수의 역 푸리에 변환이다. 이 보간식은 Whitaker-Shannon 보간 공식과 같은 고차원이다.

예를 들어 $\Omega {\displaystyle \mathrm{}}$ ${\displaystyle \Oomega}$이(가) 원형 디스크라고$$ 가정하십시오.그림 3은 피터슨-미들턴 정리 조건이 충족되었을 때$$ $f{\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle {\stackrel{}{^}}_{}}$ ${\displaystyle s_{}}$ (${\displaystyle {}_{}}$) ${\displaystyle {\f}_{s}(\cdot )}$의 지지를 나타낸다.스펙트럼 반복이 겹치지 않고 따라서 원래의 스펙트럼을 정확히 복구할 수 있다는 것을 알 수 있다.

시사점

앨리어싱

그 정리는 샘플링된 샘플링의 완벽한 재구성을 위한 샘플링 격자에 대한 조건을 제공한다.격자가 Petersen-Middleton 조건을 만족시킬 만큼 충분히 미세하지 않은 경우, 필드는 일반적으로 표본으로부터 정확히 재구성될 수 없다.이 경우에 우리는 샘플이 별칭이 될 수 있다고 말한다.다시 $\Omega {\displaystyle \mathrm{}}$ ${\displaystyle \Oomega}$이(가) 원형 디스크인$$ 예를 들어 보십시오.Petersen-Middleton 조건이 유지되지 않는 경우, 샘플링된 스펙트럼의 지원은 그림 4와 같다.이 경우 스펙트럼 반복이 중첩되어 재구성에 앨리어싱이 발생한다.

앨리어싱의 간단한 삽화는 저해상도 영상을 연구함으로써 얻을 수 있다.회색조 이미지는 2차원 공간의 함수로 해석할 수 있다.앨리어싱의 예는 그림 5의 벽돌 패턴 영상에 나타나 있다.이미지는 샘플링 정리의 조건이 충족되지 않을 때 앨리어싱의 효과를 보여준다.픽셀의 격자가 장면에 적합할 정도로 미세하지 않은 경우, 획득한 영상에서 Moiré 패턴의 출현으로 증명된 대로 앨리어싱이 발생한다.그림 6의 이미지는 씬(scene)의 평활화된 버전이 동일한 격자로 샘플링될 때 얻는다.이 경우 정리의 조건이 충족되고 별칭은 발생하지 않는다.

1978년 Bauman Moscow State Technical University의 S. P. Efimov는 주파수 영역의 제한을 완화하기 위한 접근법을 발견했다.^[3]그는 N개의 동일한 샘플링 격자를 서로 임의로 이동시킬 것을 고려했다.최적의 샘플링은 상호 격자 상의 N번으로 이동된 버전의 주파수 영역에 유효하다.따라서 링은 한 개 대신 육각형 세트로 겹칠 수 있다.제임스 웹 우주 망원경 배열은 18개의 육각형으로 이루어져 있다.배열 신호의 2-d 푸리에 변환(즉, 방출 신호의 경우)에는 18개의 시프트 래치에서 샘플링이 가능하다.

최적 표본 추출 격자

${\displaystyle {umbern}^{}}$ ${\$의 단위 공간 볼륨당 샘플링 포인트의 밀도, 즉 최소 샘플링 밀도로 이어지는 포인트의 구성을 파악하는 것이 수족 제한 필드의 샘플링 계획을 설계하는 데 관심 있는 대상 중 하나이다$.$ 일반적으로 측정치를 가져오고 저장하는 데 드는 비용은 프로다.채택된 샘플링 밀도에 대한 포텐셜.실제로 2차원 장을 표본으로 추출하는 자연적 접근방식은 직사각형 격자의 지점에서 표본을 추출하는 것이다.그러나 이것이 샘플링 밀도 측면에서 항상 이상적인 선택은 아니다.The theorem of Petersen and Middleton can be used to identify the optimal lattice for sampling fields that are wavenumber-limited to a given set ${\displaystyle \Omega \subset \Re ^{d}}$. For example, it can be shown that the lattice in ${\displaystyle \Re ^{2}}$ with minimum spatial density of points that admits pe$\Re {\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$의 원형 디스크로 제한된 필드의 감염 재구성은 육각 격자형 격자다$$.^[4]따라서 $\Re {\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$의 등방성 필드를 샘플링하는 데 육각 래티스가 선호된다$.$

최적의 샘플링 격자는 더 높은 차원에서 연구되었다.^[5]일반적으로 최적의 구면 포장 래티스는 부드러운 확률적 공정 표본 추출에 이상적이며, 래티스를^[6] 덮는 최적의 구면은 거친 확률적 공정 표본 추출에 이상적이다.

일반적으로 최적의 격자는 분리할 수 없기 때문에 보간 및 재구성 필터를 설계하려면 비텐서 제품(즉, 분리할 수 없는) 필터 설계 메커니즘이 필요하다.박스 스플라인들은 각 격자에 기하학적으로 맞춤화할 수 있는 그러한 분리 불가능한 재구성 FIR 필터를 설계하기 위한 유연한 프레임워크를 제공한다.^[7][8]육각형^[9](육각형)은 2-D 육각형 래티스의 B-스플라인을 일반화한 것이다.마찬가지로, 3-D 이상 치수에서 보로노이 스플라인^[10](Voronoi spline)은 최적의 격자를 포함하여 모든 격자에 기하학적으로 맞춤화된 분리 불가능한 FIR 필터를 설계하는 데 사용할 수 있는 B-spline의 일반화를 제공한다.

최적의 격자로 일반화된 이상적인 저역-통과 필터(즉, sinc 함수)의 명시적 구성은 이러한 격자(Zonotope)의 브릴루인 영역(위의$$ $\Omega {\displaystyle \mathrm{}}$ ${\displaystyle \Oomega })$의 기하학적 특성을 연구함으로써 가능하다.^[11]이 접근방식은 최적의 샘플링 래치를 포함하여 일반 래치에 대해$$$for{\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle {\Omega }_{\mathrm{}}}$ ( ${\displaystyle {}_{}}$ )$displaystyle {\chi }_{\Oomega }(\cdot )}$의 폐쇄형 명시적 표현을 제공한다.이 구조는 Lanczos 필터를 1-D 단위의 다차원 설정으로 일반화하여 최적의 격자를 제공한다.^[11]

적용들

피터슨-미들턴 정리는 지진 조사, 환경 모니터링 및 공간 오디오 필드 측정과 같은 공간 현상의 측정을 포함하는 애플리케이션에서 효율적인 센서 배치 전략을 설계하는 데 유용하다.

참조