다변량 적응형 회귀 분석 스플라인
Multivariate adaptive regression spline통계학에서 다변량 적응 회귀 스플라인(MARS)은 1991년 [1]Jerome H. Friedman에 의해 도입된 회귀 분석의 한 형태입니다.비모수 회귀 분석 기법이며 변수 간의 비선형성과 교호작용을 자동으로 모형화하는 선형 모형의 확장으로 볼 수 있습니다.
"MARS"라는 용어는 Salford Systems에 상표 및 라이선스를 부여합니다.상표권 침해를 피하기 위해 MARS의 많은 오픈 소스 구현은 "Earth"[2][3]라고 불립니다.
기본
이 섹션에서는 몇 가지 예를 사용하여 MARS에 대해 설명합니다.데이터 집합(입력 변수 x의 행렬 및 관측된 반응 y의 벡터)부터 시작합니다. 각 행에 대한 반응은 x에 있습니다. 예를 들어, 데이터는 다음과 같습니다.
| x | y |
|---|---|
| 10.5 | 16.4 |
| 10.7 | 18.8 |
| 10.8 | 19.7 |
| ... | ... |
| 20.6 | 77.0 |
여기에는 독립 변수가 하나만 있으므로 x 행렬은 하나의 열일 뿐입니다.이러한 측정을 바탕으로 주어진 x에 대한 기대 y를 예측하는 모형을 만들고자 합니다.
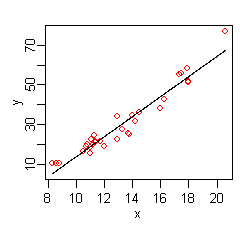
는로부터 을 나타냅니다오른쪽 그림은 이 함수의 플롯을 나타내고 있습니다.된y 대 x를 나타내는 선으로 y의 원래 값은 빨간색 점으로 표시됩니다.
x의 극한에 있는 데이터는 y와 x 사이의 관계가 비선형일 수 있음을 나타냅니다(x의 낮은 값과 높은 값의 회귀선에 상대적인 빨간색 점을 참조하십시오).따라서 비선형성을 고려한 모델을 자동으로 구축하기 위해 MARS로 눈을 돌립니다.MARS 소프트웨어는 다음과 같이 지정된x 와 y 에서 모델을 구축합니다.
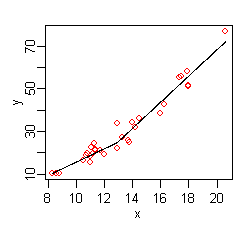
오른쪽 그림은 이 함수의 플롯을 나타내고 있습니다.된y { 대 x(원래 값 y)는 다시 빨간색 점으로 표시됩니다.이제 예측 반응이 원래 y 값에 더 잘 적합됩니다.
MARS는 비선형성을 고려하기 위해 예측된y의 꼬임이 자동으로 생성되었습니다.힌지 기능에 의해 꼬임이 발생합니다.힌지 함수는로 하는 표현입니다여기서 ( ) { ) }는 b { a} , { b} ) 、b { displaystyle b) 。힌지 기능은 아래에 자세히 설명되어 있습니다.
이 간단한 예제에서는 그래프에서 y가 x와 비선형 관계임을 쉽게 알 수 있습니다(또한 y가 x의 제곱에 따라 변동한다고 추측할 수도 있습니다).그러나 일반적으로 여러 개의 독립 변수가 존재하며 y와 이러한 변수 간의 관계는 명확하지 않고 그림으로 쉽게 볼 수 없습니다.MARS를 사용하여 비선형 관계를 검출할 수 있습니다.
변수가 여러 개인 MARS 식의 예를 다음에 나타냅니다.
이 식은 기온 및 기타 몇 가지 변수의 함수로 대기 오염(오존 수준)을 모델링합니다.공식의 마지막 항(마지막 줄)에는 n \ 와 s\ 의 상호작용이 포함되어 있습니다.
오른쪽 그림은 d\ \{ 및 s\ \ \{이(가) 다르며 다른 변수는 중앙값으로 고정되므로 n \ \ { 을(를) 그림에 나타냅니다.이 수치는 가시성이 낮지 않는 한 바람이 오존 수준에 영향을 미치지 않는다는 것을 보여준다.MARS는 힌지 기능을 조합함으로써 상당히 유연한 회귀 표면을 구축할 수 있습니다.
위의 식을 얻기 위해 MARS 모델 구축 절차에서는 사용하는 변수(일부 변수는 중요하지만 다른 변수는 중요하지 않음), 힌지 함수 내의 꼬임 위치 및 힌지 함수 조합 방법을 자동으로 선택합니다.
MARS 모델
MARS는 이 형식의 모델을 구축합니다.
이 모델은 기본 의 가중치 합입니다. 각 는 계수입니다.예를 들어, 위의 오존 공식의 각 선은 계수를 곱한 하나의 기준 함수이다.
각 기본 i () {는 다음 세 가지 형식 중 하나를 취합니다.
1) 상수 1.그런 용어가 딱 하나 있는데, 절편이에요.위의 오존 공식에서 절편 항은 5.2입니다.
2) 힌지 기능.힌지 함수는max ( , -) { , x - { \ {} } } ( 0 , \ { constant - x ) 。MARS는 힌지 함수의 매듭에 대해 변수와 값을 자동으로 선택합니다.이러한 기준 함수의 예는 오존 공식의 중간 세 줄에서 볼 수 있다.
3) 2개 이상의 힌지 기능을 가진 제품.이러한 기준 함수는 두 개 이상의 변수 간의 교호작용을 모형화할 수 있습니다.예를 들어 오존 공식의 마지막 라인이 있습니다.
힌지 기능
MARS 모델의 주요 부분은 다음 형식을 취하는 힌지 기능입니다.
또는
서 cc는 매듭이라고 하는 상수입니다.오른쪽 그림은 3.1에 매듭이 있는 힌지 기능의 미러 쌍을 보여줍니다.
힌지 함수는 범위의 일부에 대해 0이므로 데이터를 분리된 영역으로 분할하는 데 사용할 수 있으며, 각 영역은 독립적으로 처리될 수 있습니다.예를 들어, 식에서 힌지 함수의 대칭 쌍은
는 전 항에서 설명한 단순한 MARS 모델에 대해 나타낸 분할 선형 그래프를 작성합니다.
힌지 함수에서 부분 선형 함수만 형성될 수 있다고 생각할 수 있지만 힌지 함수를 함께 곱하여 비선형 함수를 형성할 수 있습니다.
힌지 기능은 램프, 하키 스틱 또는 정류기 기능이라고도 합니다. 문서에서 사용되는 \ 표기법 대신 힌지 함수는 ( -)+ + {로 표시됩니다.
모델 구축 프로세스
MARS는 전진 패스와 후진 패스의 2가지 단계로 모델을 구축합니다.이 2단계 접근법은 재귀 파티션 트리에서 사용되는 접근법과 동일합니다.
포워드 패스
MARS는 가로채기 용어(응답값의 평균)만으로 구성된 모델부터 시작합니다.
다음으로 MARS는 모델에 쌍으로 기본 함수를 반복적으로 추가합니다.각 단계에서 제곱합 잔차 오차의 최대 감소를 제공하는 기본 함수 쌍을 찾습니다(욕심 알고리즘).쌍의 두 기본 함수는 미러 힌지 함수의 다른 면이 각 기능에 사용된다는 점을 제외하고 동일합니다.각 새 기준 함수는 모형에 이미 있는 항(절편 항일 수 있음)에 새 힌지 함수를 곱한 값으로 구성됩니다.힌지 함수는 변수와 노트로 정의되므로 새로운 기본 함수를 추가하려면 MARS는 다음 항목의 모든 조합을 검색해야 합니다.
1) 기존 용어(이 문맥에서는 부모 용어라고 부릅니다.
2) 모든 변수(새로운 기준 함수를 위해 하나를 선택)
3) 각 변수의 모든 값(새로운 힌지 기능의 매듭)
각 항의 계수를 계산하기 위해 MARS는 해당 항의 선형 회귀를 적용합니다.
이 항 추가 공정은 잔차 오차의 변화가 너무 작아서 계속할 수 없거나 항이 최대 수에 도달할 때까지 계속됩니다.최대 항 수는 모델 구축을 시작하기 전에 사용자가 지정합니다.
각 스텝에서의 검색은 brute-force 방식으로 이루어지지만 힌지 함수의 특성상 고속 최소 제곱 갱신 기술을 사용하여 검색이 비교적 빠르게 이루어질 수 있다는 것이 MARS의 주요 특징입니다.사실, 수색은 폭력적이지 않습니다.각 단계에서 고려하는 상위 용어('Fast MARS')[4]의 수를 줄이는 휴리스틱을 사용하여 검색 속도를 높일 수 있습니다.
백패스
전진 패스는 일반적으로 오버핏 모델을 구축합니다.과적합 모형은 모형을 구축하는 데 사용되는 데이터에는 적합하지만 새 데이터에는 잘 일반화되지 않습니다.더 나은 일반화 능력을 가진 모형을 구축하기 위해 역방향 패스는 모형을 자외선으로 만듭니다.최적 하위 모형을 찾을 때까지 각 단계에서 가장 효과적이지 않은 항을 하나씩 삭제하고 항을 하나씩 제거합니다.모델 서브셋은 아래에 설명된 Generalized Cross Validation(GCV) 기준을 사용하여 비교됩니다.
역방향 패스는 포워드 패스보다 장점이 있습니다.즉, 임의의 스텝에서 삭제할 용어를 선택할 수 있지만 각 스텝의 포워드 패스는 다음 쌍의 용어만 볼 수 있습니다.
정방향 패스는 쌍으로 항을 추가하지만 역방향 패스는 일반적으로 쌍의 한 쪽을 파기하므로 최종 모형에서는 항이 쌍으로 표시되지 않는 경우가 많습니다.위의 첫 번째 MARS 예제에서y {y에 등식에서 쌍으로 구성된 힌지를 볼 수 있습니다. 오존 예제에는 완전한 쌍이 유지되지 않습니다.
일반 교차 검증
역방향 패스에서는 Generalized Cross Validation(GCV; 일반화 교차 검증)을 사용하여 모델 서브셋의 성능을 비교하여 최적의 서브셋을 선택합니다.GCV 값이 작을수록 좋습니다.GCV는 정규화의 한 형태입니다. 즉, 모델의 복잡성과 적합도를 비교합니다.
모형이 교육 데이터가 아닌 새 데이터에 대해 얼마나 잘 수행되는지 추정하려고 합니다.이러한 새로운 데이터는 모델 구축 시점에서는 일반적으로 사용할 수 없기 때문에 GCV를 사용하여 새로운 데이터의 성능을 추정합니다.트레이닝 데이터의 Raw residual-sum-of-squares(RSS; 미가공 잔차합)는 모델을 비교하기에 불충분합니다.이는 MARS 용어가 삭제되면 RSS가 항상 증가하기 때문입니다.즉, RSS를 사용하여 모델을 비교한 경우, 역방향 패스는 항상 가장 큰 모델을 선택하지만 일반적으로 가장 큰 모델의 일반화 퍼포먼스가 가장 뛰어나지 않습니다.)
GCV의 공식은
- GCV = RSS / (N · (유효 파라미터 수) / N)2
여기서 RSS는 교육 데이터에 대해 측정된 잔차 제곱합이고 N은 관측치의 수(x 행렬의 행 수)입니다.
Effective Number Of Parameters는 MARS 컨텍스트에서 다음과 같이 정의됩니다.
- (유효한 파라미터 수) = (화성항 수) + (화성항 수) · (화성항 수) - 1 ) / 2
여기서 penalty는 약2 또는 3입니다(MARS 소프트웨어에서는 사용자가 사전에 패널티를 설정할 수 있습니다).
주의:
- (화성 용어 수 - 1 ) / 2
힌지 기능 매듭의 수이므로 공식은 매듭의 추가에 불이익을 줍니다.따라서 GCV 공식은 모델의 유연성을 고려하여 훈련 RSS를 조정(즉 증가)합니다.너무 유연한 모델은 데이터의 체계적 구조뿐만 아니라 데이터에서 노이즈의 특정 실현을 모델링하기 때문에 유연성에 불이익을 준다.
일반화된 교차 검증은 공식을 사용하여 생략된 원아웃 검증에 의해 결정되는 오류를 근사하기 때문에 이러한 이름이 붙습니다.그것은 단지 근사치이지만 실제로 잘 작동한다.GCV는 Craven과 Wahba에 의해 도입되었으며 MARS를 위해 Friedman에 의해 확장되었습니다.
제약
한 가지 제약조건은 이미 언급되어 있습니다.즉, 사용자는 포워드 패스의 최대 용어 수를 지정할 수 있습니다.
최대 허용 상호작용도를 지정함으로써 포워드 패스에 더 많은 제약을 가할 수 있다.일반적으로 교호작용은 1~2도만 허용되지만 데이터가 교호작용을 보증하는 경우에는 더 높은 차수를 사용할 수 있습니다.위의 첫 번째 MARS 예에서 최대 상호작용 정도는 1개(즉, 상호작용 또는 가법 모델 없음)이며, 오존 예에서는 2개입니다.
포워드 패스에 다른 제약이 있을 수 있습니다.예를 들어 사용자는 특정 입력 변수에 대해서만 상호 작용을 허용하도록 지정할 수 있습니다.이러한 제약은 데이터를 생성한 프로세스에 대한 지식이 있기 때문에 의미가 있을 수 있습니다.
장점과 단점
어떤 회귀 모형화 기법도 모든 상황에 최적이지는 않습니다.다음 가이드라인은 MARS의 장점과 단점을 설명하기 위한 것입니다만, 가이드라인에는 예외가 있습니다.MARS를 재귀 파티션과 비교하는 것은 도움이 됩니다.이 작업은 다음과 같습니다.(재귀 파티셔닝은 일반적으로 회귀 트리, 의사 결정 트리 또는 CART라고도 합니다. 자세한 내용은 재귀 파티션 문서를 참조하십시오.)
- MARS 모델은 선형 회귀 모델보다 유연합니다.
- MARS 모델은 이해하기 쉽고 [5]해석하기 쉽습니다.위의 오존 농도 방정식을 예를 들어 훈련된 뉴럴 네트워크 또는 랜덤 포레스트의 내부와 비교하십시오.
- MARS는 연속 [6][7]데이터와 범주형 데이터를 모두 처리할 수 있습니다.MARS는 수치 데이터의 재귀 분할보다 나은 경향이 있습니다.이는 재귀 분할에 의해 사용되는 단계별 상수 분할보다 숫자 변수에 힌지가 더 적합하기 때문입니다.
- MARS 모델을 구축하기 위해 데이터 준비가 거의 [5]또는 전혀 필요하지 않은 경우가 많습니다.힌지 함수는 입력 데이터를 자동으로 분할하므로 특이치의 효과가 포함됩니다.이 점에서 MARS는 다른 방법을 사용하지만 데이터를 분리된 영역으로 분할하는 재귀 파티셔닝과 비슷합니다.(다만, 대부분의 통계 모델링 기법과 같이,[citation needed] MARS 모델을 트레이닝 하기 전에, 기존의 이상치를 삭제하도록 고려할 필요가 있습니다).
- MARS(재귀 분할과 마찬가지로)는 자동 변수 선택을 수행합니다(즉, 모델에 중요한 변수가 포함되고 중요하지 않은 변수는 제외됩니다).그러나, 특히 상관된 예측 변수가 있는 경우 선택에 일부 임의성이 있을 수 있으며, 이는 해석 가능성에 영향을[5] 미칠 수 있다.
- MARS 모델은 바이어스와 분산의 트레이드오프가 양호한 경향이 있습니다.모델은 비선형성 및 가변 상호작용을 모델링할 수 있을 정도로 유연하지만(따라서 MARS 모델의 바이어스는 상당히 낮지만) MARS 기본 함수의 제약된 형식이 너무 많은 유연성을 방지합니다(따라서 MARS 모델의 분산은 상당히 낮습니다).
- MARS는 꽤 큰 데이터 세트를 처리하는 데 적합합니다.예를 들어 100개의 예측 변수와5 10개의 관측치를 가진 입력 행렬에서 MARS 모델을 구축하는 것은 일상적인 일입니다.이러한 모델은 MARS 용어의 최대 상호작용 정도가 1로 제한된다고 가정할 때 1GHz 머신에서 약 1분 만에 구축할 수 있습니다(즉, 가법 용어만 해당).동일한 1GHz 머신에서 동일한 데이터를 사용하는 수준2 모델은 시간이 더 오래 걸립니다.약 12분 정도 걸립니다.이러한 시간은 데이터에 크게 의존합니다.재귀 파티셔닝은 [citation needed]MARS보다 훨씬 빠릅니다.
- MARS 모델에서는 비모수 회귀 분석과 마찬가지로 모델에 대한 파라미터 신뢰 구간 및 기타 체크는 선형 회귀 모델과 달리 직접 계산할 수 없습니다.대신 교차 검증 및 관련 기법을 사용하여 모형을 검증해야 합니다.
- MARS 모델은 부목만큼 적합하지는 않지만, 훨씬 더 빠르게 구축할 수 있고 해석도 더 용이합니다.('해석 가능한' 모형은 각 예측 변수의 효과를 명확하게 하는 형식입니다.)
- 그
earth,mda,그리고.polspline구현에서는 예측 변수의 결측값을 허용하지 않지만 회귀 트리의 자유로운 구현(예:rpart그리고.party)는 대리 분할이라고 불리는 기술을 사용하여 결측값을 허용합니다. - MARS 모델은 신속하게 예측을 할 수 있습니다.예측함수는 MARS 모델식을 평가하기만 하면 됩니다.이를 Support Vector Machine(지원 벡터 머신)과 비교해 보십시오. 여기서 모든 변수는 모든 지원 벡터의 해당 요소에 곱해야 합니다.변수가 많고 벡터를 지원하는 경우가 많으면 처리 속도가 느려질 수 있습니다.
- 결과적으로 장착된 기능은 부드럽지 않습니다(힌지를 따라서는 구별되지 않음).
- Generalized Linear Model(GLM; 일반화 선형 모델)은 MARS 모델 구축 후 링크 함수를 적용하여 MARS 모델에 통합할 수 있습니다.따라서 예를 들어 MARS 모델은 로지스틱 회귀 분석을 사용하여 확률을 예측할 수 있습니다.
- 비선형 회귀 분석은 함수의 기본 형식을 알고 있고 회귀 분석은 해당 함수의 모수를 추정하는 데만 사용됩니다.한편, MARS는 기능의 성질에 엄격한 제약이 있지만 기능 자체를 추정합니다.(데이터에서 모형을 찾는 것은 모형에 제약 조건이 없으면 제대로 배치되지 않는 역문제이기 때문에 이러한 제약 조건이 필요합니다.)
- 재귀 파티셔닝(일반적으로 CART라고 불립니다). MARS는 모델이 수치(비범주형) 데이터를 보다 잘 처리할 수 있도록 하는 재귀 파티셔닝의 일반화라고 볼 수 있습니다.
- 일반화 가법 모형.사용자의 관점에서 GAM은 MARS와 유사하지만 (a) MARS 기반 함수 대신 부드러운 황토 또는 다항식 스플라인에 적합하며 (b) 변수 상호작용을 자동으로 모델링하지 않는다.GAM이 내부적으로 사용하는 피팅 방식은 MARS와 매우 다릅니다.가변 상호작용의 자동 검출을 필요로 하지 않는 모델의 경우 GAM은 MARS와 경쟁하는 경우가 많습니다.
- TSMARS. Time Series Mars는 MARS 모델이 시계열 컨텍스트에서 적용될 때 사용되는 용어입니다.일반적으로 이 설정에서는 예측 변수가 지연된 시계열 값이며 이로 인해 자기 회귀 스플라인 모델이 생성됩니다.이동 평균 스플라인 모델을 포함하는 이러한 모델과 확장은 "TSMARS를 사용한 단변량 시계열 모델링 및 예측: TSMARS를 사용한 임계 시계열 자기 회귀, 계절 및 이동 평균 모델의 연구"에 설명되어 있다.
- 베이지안 MARS(BMARS)는 동일한 모델 형식을 사용하지만 베이지안 방식을 사용하여 모델을 구축합니다.모델 구축 방법이 다르기 때문에 최적의 MARS 모델이 다를 수 있습니다.BMARS의 결과는 일반적으로 확률론적 [8]예측을 가능하게 하는 MARS 모델의 후방 샘플의 합체이다.
「 」를 참조해 주세요.
레퍼런스
- ^ Friedman, J. H. (1991). "Multivariate Adaptive Regression Splines". The Annals of Statistics. 19 (1): 1–67. CiteSeerX 10.1.1.382.970. doi:10.1214/aos/1176347963. JSTOR 2241837. MR 1091842. Zbl 0765.62064.
- ^ CRAN 패키지 접지
- ^ 접지 – 주황색(Python 기계 학습 라이브러리)의 다변량 적응형 회귀 스플라인
- ^ Friedman, J. H. (1993) Fast MARS, Stanford University Statistics Department, Technical Report 110
- ^ a b c Kuhn, Max; Johnson, Kjell (2013). Applied Predictive Modeling. New York, NY: Springer New York. doi:10.1007/978-1-4614-6849-3. ISBN 9781461468486.
- ^ Friedman, Jerome H. (1993). "Estimating Functions of Mixed Ordinal and Categorical Variables Using Adaptive Splines". In Stephan Morgenthaler; Elvezio Ronchetti; Werner Stahel (eds.). New Directions in Statistical Data Analysis and Robustness. Birkhauser.
- ^ Friedman, Jerome H. (1991-06-01). "Estimating Functions of Mixed Ordinal and Categorical Variables Using Adaptive Splines". DTIC. Archived from the original on April 11, 2022. Retrieved 2022-04-11.
- ^ DENISON, D. G. T.; MALLICK, B. K.; SMITH, A. F. M. (1 December 1998). "Bayesian MARS" (PDF). Statistics and Computing. 8 (4): 337–346. doi:10.1023/A:1008824606259. ISSN 1573-1375.
추가 정보
- Hastie T., Tibshirani R. 및 Friedman J.H.(2009) The Elements of Statistical Learning, 제2판.Springer, ISBN 978-0-387-84857-0(MARS에 관한 섹션이 있습니다)
- Farway J. (2005) R, CRC, ISBN 978-1-58488-424-8에 의한 리니어 모델 확장(MARS를 R과 함께 사용하는 예 있음)
- Heping Zhang and Burton H. Singer (2010) 재귀 파티셔닝 및 응용 프로그램, 제2판.Springer, ISBN 978-1-4419-6823-4(MARS에 관한 장과 알고리즘의 몇 가지 조정에 대해 설명합니다)
- Denison D.G.T., Holmes C.C., Mallick B.K. 및 Smith A.F.M.(2004) 비선형 분류 및 회귀를 위한 베이지안 방법, Wiley, ISBN 978-0471-490-36-436-436-436
- Berk R.A. (2008) 회귀 관점에서 본 통계학습, Springer, ISBN 978-0-387-77500-5
외부 링크
이 문서의 외부 링크 사용은 Wikipedia의 정책 또는 지침을 따르지 않을 수 있습니다.한 외부 링크나 한 외부 를 하고, 유용한 링크를로 하여 이 를 바랍니다. (2016년 ( 템플릿메시지 및) |
MARS 타입의 모델에는, 몇개의 무료 및 상용 소프트웨어 패키지가 준비되어 있습니다.
- 무료 소프트웨어
- R 패키지:
- 매트랩 코드:
- ARSLab: Matlab용 적응형 회귀 스플라인 도구 상자
- Bayesian MARS의 비선형 분류[1] 및 회귀를 위한 Bayesian Methods의 코드.
- 파이썬
- 접지 – 다변량 적응형 회귀 스플라인
- 화이토
- 베이지안 MARS의 pyBASS.
- 상용 소프트웨어
- ^ Denison, D. G. T.; Holmes, C. C.; Mallick, B. K.; Smith, A. F. M. (2002). Bayesian methods for nonlinear classification and regression. Chichester, England: Wiley. ISBN 978-0-471-49036-4.









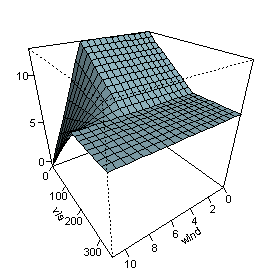


 (를) 그림에 나타냅니다.이 수치는 가시성이 낮지 않는 한 바람이 오존 수준에 영향을 미치지 않는다는 것을 보여준다.MARS는 힌지 기능을 조합함으로써 상당히 유연한 회귀 표면을 구축할 수 있습니다.
(를) 그림에 나타냅니다.이 수치는 가시성이 낮지 않는 한 바람이 오존 수준에 영향을 미치지 않는다는 것을 보여준다.MARS는 힌지 기능을 조합함으로써 상당히 유연한 회귀 표면을 구축할 수 있습니다. 




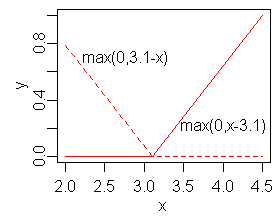


 하는 상수입니다.오른쪽 그림은 3.1에 매듭이 있는 힌지 기능의 미러 쌍을 보여줍니다.
하는 상수입니다.오른쪽 그림은 3.1에 매듭이 있는 힌지 기능의 미러 쌍을 보여줍니다.
![[\pm (x_{i}-c)]_{+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4164761539b8c42b6abe93e151683852d9ec043)
![[\cdot ]_{+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0196f79f9c7c8c6a7777ab193018b24c6f4b1a92) 표시됩니다.
표시됩니다. 

