세그먼트 회귀 분석

분할 회귀 분석(segmented regression)은 독립 변수를 구간으로 분할하고 별도의 선 세그먼트를 각 구간에 적합시키는 회귀 분석의 방법이다. 분할 회귀 분석은 다양한 독립 변수를 분할하여 다변량 데이터에 대해서도 수행할 수 있다. 분할 회귀 분석은 독립 변수가 서로 다른 그룹으로 군집화되어 이러한 영역의 변수 간에 서로 다른 관계를 나타낼 때 유용하다. 세그먼트 사이의 경계는 중단점이다.

분할된 선형 회귀 분석은 분할된 회귀 분석이며, 여기서 구간 간의 관계를 선형 회귀 분석을 통해 얻는다.

세그먼트 선형 회귀 분석, 두 개의 세그먼트

1사지 수평

위로 기울어진 1사지

아래로 기울어진 1사지

두 개의 세그먼트를 중단점으로 구분한 세그먼트 선형 회귀 분석은 다양한 영향력 있는 요인(x)의 반응 함수(Yr)의 갑작스러운 변화를 정량화하는 데 유용할 수 있다. 중단점은 (미필요 효과가) 발생하는 임계, 안전 또는 임계값 이상으로 해석할 수 있다. 중단점은 의사 결정에서 중요할 수 있다.

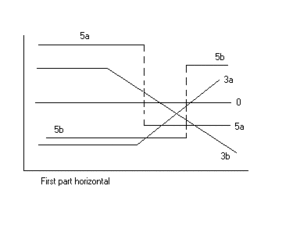
그림은 얻을 수 있는 일부 결과와 회귀 유형을 예시한다.

세그먼트 회귀 분석은 (y, x ) 데이터 집합의 존재를 기반으로 하며, 여기서 y는 종속 변수이고 x 독립 변수다.

각 세그먼트에 개별적으로 적용되는 최소 제곱법, 즉 종속 변수의 관측된 (y) 값과 계산된 (Yr) 값 사이의 차이(SSD) 제곱합은 최소화하면서 두 회귀선이 데이터 세트를 최대한 가깝게 맞도록 만들어지는 방법은 다음과 같은 두 개의 방정식을 산출한다.

Yr = x < BP(차단점)의 경우₁ A.x + K₁
Yr = x₂ > BP의₂ A.x + K (차단점)

여기서:

Yr은 x의 특정 값에 대한 y의 예상(예측) 값이다.

A와₁ A는₂ 회귀 계수(선 세그먼트의 기울기를 나타냄)이다.

K와₁ K는₂ 회귀 상수(y축에서 절편을 나타냄)이다.

데이터는 많은 유형이나 추세를 보여줄 수 있다.^[2] 수치를 참조하라.

또한 두 개의 상관 계수(R):

$R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a1})^{2}}}$ R $R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{{a1}})^{2}}}$ $R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a1})^{2}}}$ $R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a1})^{2}}}$ = $R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a1})^{2}}}$ - $R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a1})^{2}}}$ ( $R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a1})^{2}}}$ - $R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a1})^{2}}}$ r $R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a1})^{2}}}$ ) $R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a1})^{2}}}$ $R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a1})^{2}}}$ $R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a1})^{2}}}$ - $R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a1})^{2}}}$ a $R_{1}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a1})^{2}}}$ ) 2 ${\$ 1}^{ $2}=1-{{\frac {\sum (y-Y_{r}}}}^{2$ }}}{{2 $}}}{{\sum (y-Y_{a1}}}}}^{2}})$ x BPoint)

, 그리고

$R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ R $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{{a2}})^{2}}}$ $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ = $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ - $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ ( $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ - $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ r $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ ) $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ - $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ ) $R_{2}^{2}=1-{\frac {\sum (y-Y_{r})^{2}}{\sum (y-Y_{a2})^{2}}}$ ${\$ }^{2 $}=1-{{\frac {\sum (y-Y_{r}}}^{$ 2}}}^{ $2}}}{{{}}}}}}}}{{{{{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

여기서:

\sum (y-Y_{r})^{2}

(

\sum (y-Y_{r})^{2}

- Y

\sum (y-Y_{r})^{2}

) 2

{\

은

\sum (y-Y_{r})^{2}

세그먼트당 최소화된 SSD임

, 그리고

Y와_a1 Y는_a2 각 세그먼트에서 y의 평균값이다.

가장 적합한 추세를 결정할 때 통계적 검사를 수행하여 이 추세가 신뢰할 수 있는지(중대한지) 확인해야 한다.

유의미한 중단점을 감지할 수 없을 때는 중단점 없이 회귀에 빠져야 한다.

예

세그먼트 선형 회귀 분석, 유형 3b

겨자수율(Yr = Ym, t/ha)과 토양 염도율(x = Ss, dS/m에서 토양용액 EC의 전기전도도로 표현) 사이의 관계를 나타내는 오른쪽의 파란색 그림의 경우 다음이 확인된다.^[3]

BP = 4.93, A = 0₁, K₁ = 1.74, A = -0.129, K₂₂ = 2.38, R = 0.0035(중요하지 않음), R = 0.395(중대한) 및 다음 중 하나₁²₂²:

Ym = 1.74 t/ha(Ss < 4.93 (차단점)
Ym = -0.129 Ss + 2.38 t/ha(Ss > 4.93 (차단점)

토양 염도 < 4.93 dS/m>이 안전하며 토양 염도 <4.93 dS/m>이 토양 염도 단위 증가 당 0.129 t/ha의 수확량을 감소시킨다는 것을 나타낸다.

이 그림은 또한 신뢰 구간과 불확실성을 상세하게 보여준다.

테스트 절차

시계열 예제, 유형 5

분산 분석 표의 예: 이 경우 중단점의 도입은 매우 중요하다.

추세의 유형을 결정하는 데 다음과 같은 통계적 시험을 사용한다.

BP를 회귀 계수 A와₁ A의₂ 함수와 y 데이터의 Y와₁ Y와₂ x 데이터의 평균 X와₁ X(BP의 왼쪽과 오른쪽)의₂ 함수로 표현하고, BP의 표준 오차(SE)를 계산하기 위해 추가와 승수의 오차 전파 법칙을 사용하고, 학생의 t-검정을 적용함으로써 중단점(BP)의 유의성
A와₁₁ A의₂ 학생 t-분포와 표준오차 SE를 적용하는₂ A와 A의 의의
A와₁ A의₂ 차이의 SE를 사용하여 학생의 t-분포를 적용하는 차이의 유의성.
학생 차이의₂ SE를 사용하여 학생의 t-분포를 적용하는 Y와₁ Y의 차이의 유의성.
중단점의 존재 여부를 시험하기 위한 보다 공식적인 통계적 접근방식은 분할된 선을 추정할 필요가 없는 유사 점수 시험을 통해서이다.^[4]

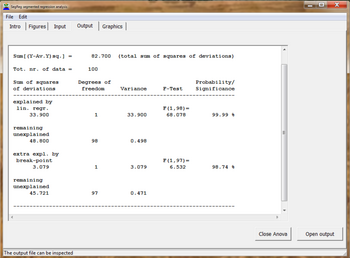
또한 모든 데이터의 상관 계수(Ra), 결정 계수 또는 설명 계수, 회귀 함수의 신뢰 구간, 분산 분석 등을 사용한다.^[5]

유의성 시험에 의해 설정된 조건에서 최대화해야 하는 모든 데이터(Cd)에 대한 결정 계수는 다음과 같다.

${\dyplaystyle C_{d}=1-{\sum(y-Y_{r})^{2} \over \sum(y-Y_{a})$

여기서 Yr은 이전의 회귀 방정식에 따른 y의 기대(예측) 값이고 Ya는 모든 y 값의 평균이다.

Cd 계수는 0(전혀 설명하지 않음) ~ 1(전체 설명, 완벽한 일치) 사이의 범위다.
순수하고 분할되지 않은 선형 회귀 분석에서 Cd와 Ra의² 값은 같다. 분할 회귀 분석에서 Cd는 분할을 정당화하기 위해 Ra보다² 상당히 커야 한다.

중단점의 최적 값은 Cd 계수가 최대가 되도록 찾을 수 있다.

효과 없음 범위

효과가 없는 X=0 ~ X=7.85 범위의 그림.

세그먼트 회귀 분석은 종종 설명 변수(X)가 종속 변수(Y)에 영향을 미치지 않는 범위를 탐지하는 데 사용되는 반면 도달 범위를 벗어나면 양수 또는 음수 중에서 명확한 반응이 나타난다. 아무런 영향도 미치지 않는 범위는 X 영역의 초기 부분이나 그 마지막 부분에서 찾을 수 있다. 그"효과가 없"분석을 위해 분절된 회귀 분석[6]에 최소한의 사각형 틀의 적용 방식이 아닐 수 있는 가장 적절한 기술이 목표이기 때문에 오히려 경사면에 크게 제로에서지만 다르다에 도달하는 동안을 넘어서 Y-X 관계 0경사의 소유로 간주할 수 있는 가장 긴 시간이므로를 찾는 것이다. kn이 경사의 가장 좋은 값에 대한 오울렛은 재료가 아니다. 무효과 범위를 찾는 방법은 범위에 걸쳐 점진적인 부분 회귀 분석으로, 회귀 계수가 0과 유의하게 다를 때까지 작은 스텝으로 범위를 확장한다.

다음 그림에서 중단점은 X=7.9에서 발견되는 반면 같은 데이터의 경우(머스타드 수확량은 위의 파란색 그림 참조), 최소 제곱법은 X=4.9에서만 중단점을 산출한다. 후자의 값은 더 낮지만 중단점을 벗어난 데이터의 적합성이 더 좋다. 따라서 어떤 방법을 사용해야 하는지는 분석의 목적에 따라 달라질 것이다.

참고 항목

참조

^ 빈도 및 회귀 분석. 제6장: H.P.Ritzema (edd, 1994), 배수 원리 및 응용, Pubm. 16, 페이지 175-224, 국제 토지 개간 및 개선을 위한 국제 연구소(ILRI), 네덜란드 와게닝겐. ISBN90-70754-33-9. 웹 페이지 [1], nr. 20 이하 또는 PDF로 직접 다운로드: [2]
^ 농업 분야 배수 연구 : 자료 분석 네덜란드 와게닝겐의 국제 토지 개간 및 개량 연구소(ILRI)의 "액체 금" 프로젝트의 일부분이다. PDF로 다운로드: [3]
^ R.J.오스터반, D.P.샤르마, K.N.싱어와 K.V.G.K.Rao, 1990, 크롭 생산과 토양 염도: 분할된 선형 회귀에 의한 인도의 현장 데이터 평가. 인: 아리드 및 반아리드 지역의 염분 관리를 위한 토지 배수에 관한 심포지엄, 1990년 2월 25일부터 3월 2일까지, 이집트 카이로, 제3권, 제5권, 세션 V, 페이지 373 - 383.
^ Muggeo, VMR (2016). "Testing with a nuisance parameter present only under the alternative: a score-based approach with application to segmented modelling" (PDF). Journal of Statistical Computation and Simulation. 86 (15): 3059–3067. doi:10.1080/00949655.2016.1149855.
^ 분산 분석 및 F-검정을 사용한 분할 선형 회귀 분석의 통계적 유의성. [4]에서 nr. 13 또는 PDF로 직접 다운로드: [5]
^ 분할 회귀 분석, 국제 토지 개간 및 개선 연구소(ILRI), 와게닝겐, 네덜란드. 웹 페이지에서 무료 다운로드 [6]
^ 네덜란드의 와게닝언, 국제 토지 개간 및 개량 연구소의 부분 회귀 분석 웹 페이지에서 무료 다운로드 [7]

[1] 빈도 및 회귀 분석. 제6장: H.P.Ritzema (edd, 1994), 배수 원리 및 응용, Pubm. 16, 페이지 175-224, 국제 토지 개간 및 개선을 위한 국제 연구소(ILRI), 네덜란드 와게닝겐. ISBN90-70754-33-9. 웹 페이지 [1], nr. 20 이하 또는 PDF로 직접 다운로드: [2]

[2] 농업 분야 배수 연구 : 자료 분석 네덜란드 와게닝겐의 국제 토지 개간 및 개량 연구소(ILRI)의 "액체 금" 프로젝트의 일부분이다. PDF로 다운로드: [3]

[3] R.J.오스터반, D.P.샤르마, K.N.싱어와 K.V.G.K.Rao, 1990, 크롭 생산과 토양 염도: 분할된 선형 회귀에 의한 인도의 현장 데이터 평가. 인: 아리드 및 반아리드 지역의 염분 관리를 위한 토지 배수에 관한 심포지엄, 1990년 2월 25일부터 3월 2일까지, 이집트 카이로, 제3권, 제5권, 세션 V, 페이지 373 - 383.

[4] Muggeo, VMR (2016). "Testing with a nuisance parameter present only under the alternative: a score-based approach with application to segmented modelling" (PDF). Journal of Statistical Computation and Simulation. 86 (15): 3059–3067. doi:10.1080/00949655.2016.1149855.

[5] 분산 분석 및 F-검정을 사용한 분할 선형 회귀 분석의 통계적 유의성. [4]에서 nr. 13 또는 PDF로 직접 다운로드: [5]

[6] 분할 회귀 분석, 국제 토지 개간 및 개선 연구소(ILRI), 와게닝겐, 네덜란드. 웹 페이지에서 무료 다운로드 [6]

[7] 네덜란드의 와게닝언, 국제 토지 개간 및 개량 연구소의 부분 회귀 분석 웹 페이지에서 무료 다운로드 [7]

[2]

[3]

[4]

[5]

Search

세그먼트 회귀 분석

네임스페이스

더

목차

세그먼트 선형 회귀 분석, 두 개의 세그먼트

예

테스트 절차

효과 없음 범위

참고 항목

참조